2021-2022学年人教版七年级数学下册5.2.1平行线同步课件(18张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.1平行线同步课件(18张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 18:38:03 | ||
图片预览





文档简介
(共18张PPT)
5.2.1 平行线
5.2 平行线及其判定
5.2.1 平行线
能判断两条直线是相交还是平行线.
能画平行线,体会平行线平行公理(确定性).
运用平行的传递性说明理由.
【学习目标】
复习旧知
思考:(1)在同一平面内,两条直线的位置关系是什么?
(2)你怎样理解平行?
新知探究
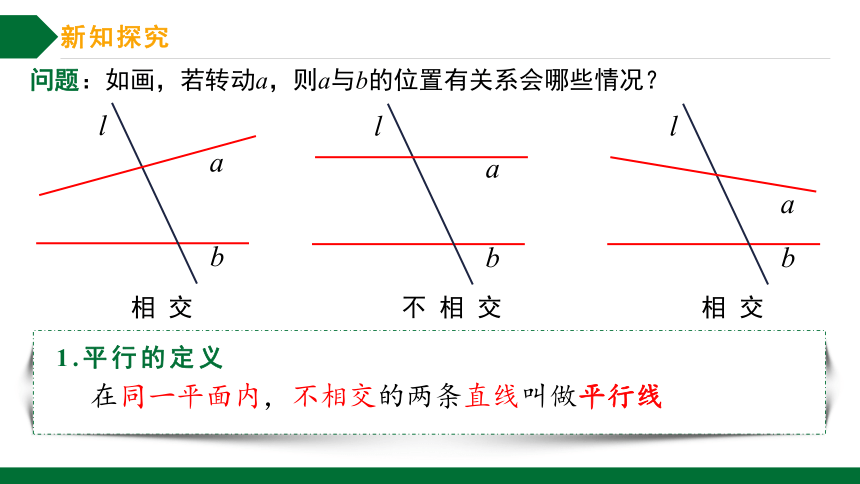
问题:如画,若转动a,则a与b的位置有关系会哪些情况?
a
b
l
相 交
a
b
l
a
b
l
不 相 交
相 交
在同一平面内,不相交的两条直线叫做平行线
1.平行的定义
思考:找出图中的平行线.
C
B
A
D
在同一平面内,不相交的两条直线叫做平行线.
AB ∥ CD
读作:“AB 平行于 CD”
问题:理解平行线的定义思考下列问题
(1)能去掉“同一平面内”这个条件吗?举例说明?
(2)在同一平面内两条直线有哪些位置关系?
(3)在同一平面内,不相交的两条线段或射线是平行吗?
C
B
A
D
在同一平面内,不相交的两条直线叫做平行线.
AB ∥ CD
读作:“AB 平行于 CD”
(1) 在同一平面内;(2) 不相交;(3) 都是直线;
平行线的定义有三个特征:
在同一平面内,不重合的两条直线只有两种位置关系:相交和平行.
活动二:画一条直线的平行线。
(1) 放;(2) 靠;(3) 推;(4) 画.
平行线的画法:
B
a
C
活动三:按要求画平行线,你从中得出什么结论?
(1)同时经过点B、C画直线BC能平行于a吗?
(2)分别经过点B、C画直线BC能平行线?
(3)你从作图得出什么结论?
b
c
平行公理:经过直线外一点,有且只有一条直线与已知直线
平行(确定性)(教材P12)
推论:如果两条直线都与第三条直线平行,那么这两条直线互相平行(传递性)(教材P12)
平行公理的推论(传递性):
如果两条直线都与第三条直线平行,那么这两条直线互相平行
c
b
a
简称:平行于第三条直线的两直线平行(传递性).
几何语言表达:
∵ a//c , c//b(已知)
∴ a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
典例讲解
例1 在如图所示的各图形中,过点M画PQ∥AB.
例2 如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
a
b
c
d
解: ∵ a ∥b,b∥c(已知),
∴ a ∥c ( 如果两条直线都与第三条直线平行,那么这两条直线互相平行 )
∵ c∥d(已知),
∴ a ∥d( 如果两条直线都与第三条直线平行,那么这两条直线互相平行 )
∵ c∥d,∴ a ∥d
(
)
课堂小结
两直线位置在同一平面内
定 义
画法
性质
相交
平行
在同一平面内,不相交的两条直线.
四步法:(1) 放;(2) 靠;(3) 推;(4) 画.
平行公理(确定性)
平行公理推论(传递性)
B
a
C
b
c
a
b
a
b
巩固练习
1.下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
2.下列说法中,错误的有( )
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
B
3.若a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.以上都不对
B
4.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条 C.1条或0条 D.无数条
C
5.在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行 B.相交 C.重合 D.以上都有可能
B
6. 如图,过P点作PQ∥AB交BC于Q,作PM∥AC交AB于M.
A
B
C
P
5.2.1 平行线
5.2 平行线及其判定
5.2.1 平行线
能判断两条直线是相交还是平行线.
能画平行线,体会平行线平行公理(确定性).
运用平行的传递性说明理由.
【学习目标】
复习旧知
思考:(1)在同一平面内,两条直线的位置关系是什么?
(2)你怎样理解平行?
新知探究
问题:如画,若转动a,则a与b的位置有关系会哪些情况?
a
b
l
相 交
a
b
l
a
b
l
不 相 交
相 交
在同一平面内,不相交的两条直线叫做平行线
1.平行的定义
思考:找出图中的平行线.
C
B
A
D
在同一平面内,不相交的两条直线叫做平行线.
AB ∥ CD
读作:“AB 平行于 CD”
问题:理解平行线的定义思考下列问题
(1)能去掉“同一平面内”这个条件吗?举例说明?
(2)在同一平面内两条直线有哪些位置关系?
(3)在同一平面内,不相交的两条线段或射线是平行吗?
C
B
A
D
在同一平面内,不相交的两条直线叫做平行线.
AB ∥ CD
读作:“AB 平行于 CD”
(1) 在同一平面内;(2) 不相交;(3) 都是直线;
平行线的定义有三个特征:
在同一平面内,不重合的两条直线只有两种位置关系:相交和平行.
活动二:画一条直线的平行线。
(1) 放;(2) 靠;(3) 推;(4) 画.
平行线的画法:
B
a
C
活动三:按要求画平行线,你从中得出什么结论?
(1)同时经过点B、C画直线BC能平行于a吗?
(2)分别经过点B、C画直线BC能平行线?
(3)你从作图得出什么结论?
b
c
平行公理:经过直线外一点,有且只有一条直线与已知直线
平行(确定性)(教材P12)
推论:如果两条直线都与第三条直线平行,那么这两条直线互相平行(传递性)(教材P12)
平行公理的推论(传递性):
如果两条直线都与第三条直线平行,那么这两条直线互相平行
c
b
a
简称:平行于第三条直线的两直线平行(传递性).
几何语言表达:
∵ a//c , c//b(已知)
∴ a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
典例讲解
例1 在如图所示的各图形中,过点M画PQ∥AB.
例2 如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
a
b
c
d
解: ∵ a ∥b,b∥c(已知),
∴ a ∥c ( 如果两条直线都与第三条直线平行,那么这两条直线互相平行 )
∵ c∥d(已知),
∴ a ∥d( 如果两条直线都与第三条直线平行,那么这两条直线互相平行 )
∵ c∥d,∴ a ∥d
(
)
课堂小结
两直线位置在同一平面内
定 义
画法
性质
相交
平行
在同一平面内,不相交的两条直线.
四步法:(1) 放;(2) 靠;(3) 推;(4) 画.
平行公理(确定性)
平行公理推论(传递性)
B
a
C
b
c
a
b
a
b
巩固练习
1.下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
2.下列说法中,错误的有( )
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
B
3.若a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.以上都不对
B
4.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条 C.1条或0条 D.无数条
C
5.在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行 B.相交 C.重合 D.以上都有可能
B
6. 如图,过P点作PQ∥AB交BC于Q,作PM∥AC交AB于M.
A
B
C
P
