人教版六年级上册5.3圆的面积同步练习(含答案)
文档属性
| 名称 | 人教版六年级上册5.3圆的面积同步练习(含答案) | 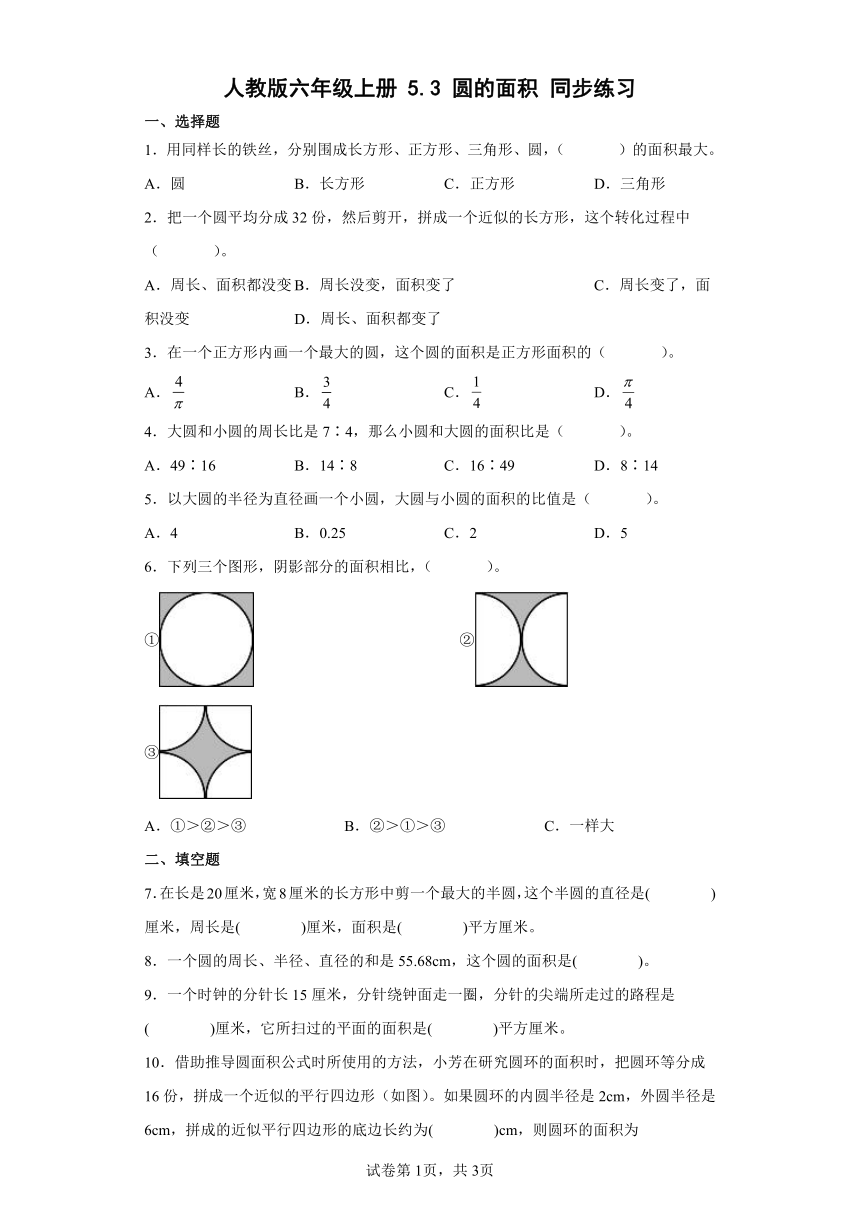 | |
| 格式 | docx | ||
| 文件大小 | 193.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 07:01:19 | ||
图片预览




文档简介
人教版六年级上册 5.3 圆的面积 同步练习
一、选择题
1.用同样长的铁丝,分别围成长方形、正方形、三角形、圆,( )的面积最大。
A.圆 B.长方形 C.正方形 D.三角形
2.把一个圆平均分成32份,然后剪开,拼成一个近似的长方形,这个转化过程中( )。
A.周长、面积都没变 B.周长没变,面积变了 C.周长变了,面积没变 D.周长、面积都变了
3.在一个正方形内画一个最大的圆,这个圆的面积是正方形面积的( )。
A. B. C. D.
4.大圆和小圆的周长比是7∶4,那么小圆和大圆的面积比是( )。
A.49∶16 B.14∶8 C.16∶49 D.8∶14
5.以大圆的半径为直径画一个小圆,大圆与小圆的面积的比值是( )。
A.4 B.0.25 C.2 D.5
6.下列三个图形,阴影部分的面积相比,( )。
① ② ③
A.①>②>③ B.②>①>③ C.一样大
二、填空题
7.在长是20厘米,宽8厘米的长方形中剪一个最大的半圆,这个半圆的直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
8.一个圆的周长、半径、直径的和是55.68cm,这个圆的面积是( )。
9.一个时钟的分针长15厘米,分针绕钟面走一圈,分针的尖端所走过的路程是( )厘米,它所扫过的平面的面积是( )平方厘米。
10.借助推导圆面积公式时所使用的方法,小芳在研究圆环的面积时,把圆环等分成16份,拼成一个近似的平行四边形(如图)。如果圆环的内圆半径是2cm,外圆半径是6cm,拼成的近似平行四边形的底边长约为( )cm,则圆环的面积为( )cm2。
三、判断题
11.半径是2厘米的圆,它的周长和面积相等。( )
12.一个圆的半径缩小到原来,周长和面积也缩小到原来的。( )
13.一个小圆和一个大圆的周长的比为2∶3,那么小圆和大圆面积的比也是2∶3。( )
14.图中阴影部分与空白部分的周长相等,面积也相等。( )
四、解答题
15.人民广场有一个半径是5m的半圆形花坛。如果要扩建这个花坛,把它的直径增加2m,花坛的面积增加了多少?
16.教室的钟表分针长10cm,从5:00到5:30,分针的尖端所走的路程是多少厘米?分针走过的面积是多少平方厘米?
17.(1)请你找出下面圆的圆心和直径,并用字母标注出来。
(2)上图中的正方形边长为10厘米,阴影部分的面积是( )平方厘米。
18.(1)以下图长方形的宽为直径在长方形内画一个半圆,并将图形的其他部分(即半圆以外的部分)画上阴影。
(2)分别求阴影部分的周长和面积。
19.爷爷用18.84m长的篱笆靠墙围了一个半圆形的鸡舍。这个鸡舍的面积是多少平方米?爷爷觉得鸡舍面积小,又沿着篱笆外围拓宽了1米,鸡舍面积扩大了多少平方米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
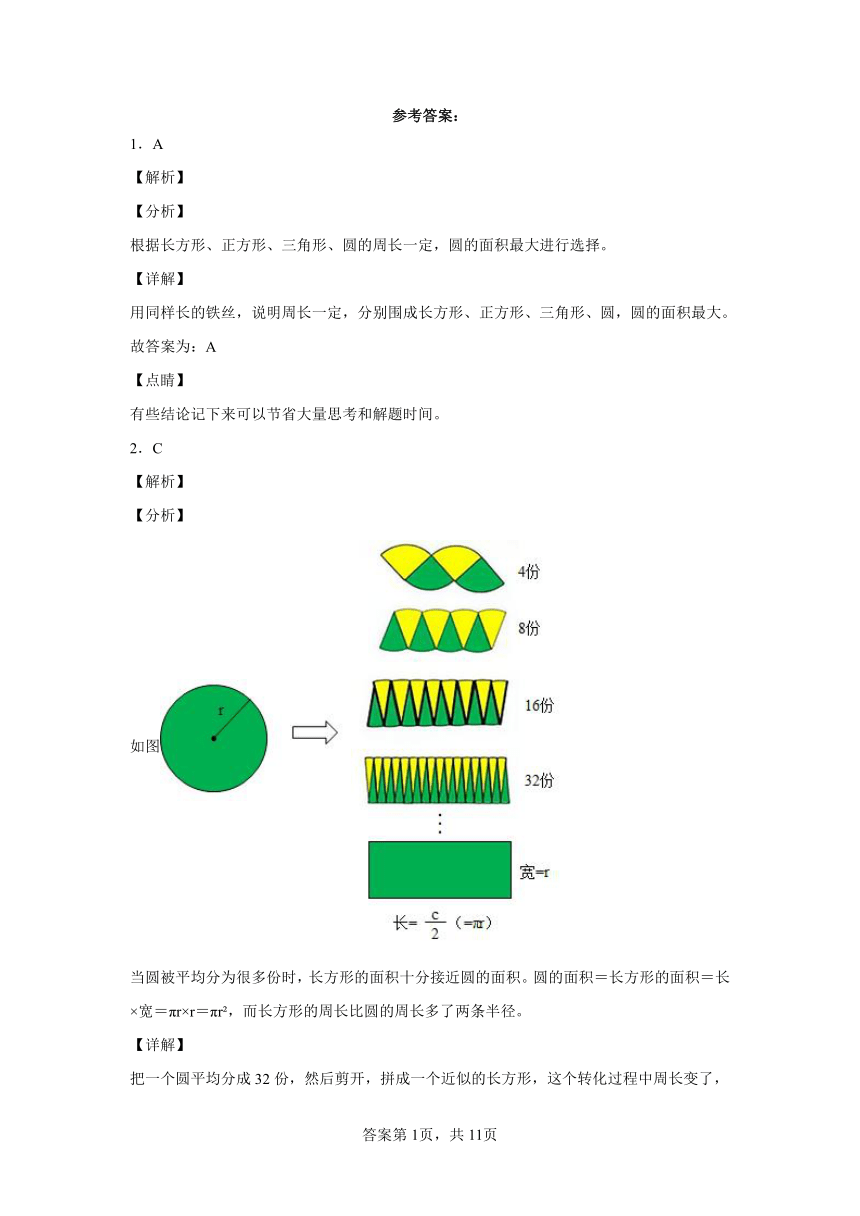
1.A
【解析】
【分析】
根据长方形、正方形、三角形、圆的周长一定,圆的面积最大进行选择。
【详解】
用同样长的铁丝,说明周长一定,分别围成长方形、正方形、三角形、圆,圆的面积最大。
故答案为:A
【点睛】
有些结论记下来可以节省大量思考和解题时间。
2.C
【解析】
【分析】
如图
当圆被平均分为很多份时,长方形的面积十分接近圆的面积。圆的面积=长方形的面积=长×宽=πr×r=πr ,而长方形的周长比圆的周长多了两条半径。
【详解】
把一个圆平均分成32份,然后剪开,拼成一个近似的长方形,这个转化过程中周长变了,面积没变。
故答案为:C
【点睛】
关键是熟悉圆的面积公式推导过程。
3.D
【解析】
【分析】
正方形内最大的圆的直径等于正方形的边长,可设圆的半径为r,则圆的直径为2r,正方形的边长为2r,由此利用圆的面积公式和正方形的面积公式即可解答。
【详解】
设圆的半径为r,则圆的直径为2r,正方形的边长为2r,
圆的面积:πr2
正方形的面积:2r×2r=4r2
πr2÷4r2=
这个圆的面积是正方形面积的。
故选:D。
【点睛】
此题主要考查的是正方形面积公式和圆的面积公式的灵活应用。
4.A
【解析】
【分析】
根据周长比的平方是面积比,进行分析。
【详解】
7 ∶4 =49∶16
故答案为:A
【点睛】
圆的面积=πr ,两数相除又叫两个数的比。
5.A
【解析】
【分析】
假设大圆的半径是2厘米,那么小圆的直径是2厘米。据此结合圆的面积公式,先分别求出大圆和小圆的面积,从而做比求出比值,选出正确选项。
【详解】
令大圆半径是2厘米,那么小圆直径是2厘米,小圆半径是1厘米。
大圆面积:3.14×22=12.56(平方厘米)
小圆面积:3.14×12=3.14(平方厘米)
12.56∶3.14=12.56÷3.14=4
所以,大圆和小圆的面积的比值是4。
故答案为:A
【点睛】
本题考查了圆的面积,灵活运用圆的面积公式是解题的关键。
6.C
【解析】
【分析】
图①圆的直径等于正方形的边长,阴影部分的面积=正方形的面积-圆的面积;
图②空白部分的两个半圆可以拼成一个圆,直径等于正方形的边长,阴影部分的面积=正方形的面积-圆的面积;
图③空白部分的四个扇形可以拼成一个圆,直径等于正方形的边长,阴影部分的面积=正方形的面积-圆的面积;
拼成的圆的面积相等,正方形的面积也相等,所以阴影部分的面积也相等,据此解答即可。
【详解】
图②和图③的空白部分可以在组成和图①空白部分相等的圆,正方形的面积也相等,所以三个图中阴影部分的面积也相等;
故答案为:C。
【点睛】
解答本题的关键要注意观察图形,确定每个图形阴影部分的面积如何计算。
7. 16 41.12 100.48
【解析】
【分析】
在长是20厘米,宽8厘米的长方形中剪一个最大的半圆,半圆的半径=长方形的宽,半径×2=直径,根据半圆的周长=πr+2r,半圆的面积=πr ÷2,计算即可。
【详解】
8×2=16(厘米)
3.14×8+16
=25.12+16
=41.12(厘米)
3.14×8 ÷2=100.48(平方厘米)
【点睛】
关键是掌握半圆的周长和面积公式。
8.113.04平方厘米
【解析】
【分析】
设半径是x厘米,则直径是2x厘米,周长是2×3.14x厘米,根据半径+直径+周长=55.68厘米,列出方程求出x的值是半径,根据圆的面积=πr ,计算即可。
【详解】
解:设半径是x厘米。
x+2x+2×3.14x=55.68
3x+6.28x=55.68
9.28x÷9.28=55.68÷9.28
x=6
3.14×6 =113.04(平方厘米)
【点睛】
关键是掌握圆的周长和面积公式。
9. 94.2 706.5
【解析】
【分析】
已知这个时钟的分针长15厘米,因为若把钟面看作一个圆,则时针相当于半径,所以要计算分针绕钟面走一圈,分针尖端所走过的路程、扫过的面积就是求圆的周长、面积。可套用公式来解答。
【详解】
C圆=2πr
=2×3.14×15
=3.14×30
=94.2(厘米)
S圆=πr2
=3.14×152
=3.14×225
=706.5(平方厘米)
【点睛】
本题需要我们展开空间思维,想象钟面及钟面上分针尖端走一圈的的样子,从而联想起圆的周长、面积计算方法,并通过相关公式来计算。
10. 25.12 100.48
【解析】
【分析】
①由题意:将一个圆环剪开,拼成一个近似的平行四边形。如果把圆环所被平均分成的每一份看作一个近似的梯形,则拼成的平行四边形的底就是由梯形的上底和下底穿插着组成的。而梯形的下底实际上是小圆周长的每一份,因此可得出:平行四边形的底边就是大圆周长与小圆周长之和的一半,可列式:(2×3.14×6+2×3.14×2)÷2=25.12(cm);
②要计算圆环的面积,有两种方法:可以通过圆环面积公式来列式;还可以转化为求平行四边形的面积来列式:25.12×(6-2)=100.48(cm2)
【详解】
①(2×3.14×6+2×3.14×2)÷2
=(3.14×12+3.14×4)÷2
=50.24÷2
=25.12(cm)
②3.14×(62-22)
=3.14×(36-4)
=3.14×32
=100.48(cm2)
25.12×(6-2)
=25.12×4
=100.48(cm2)
【点睛】
解答本题,在充分理解题意的同时,更要仔细读图。只有细致的观察图形,才能够找出圆环与平行四边形之间的联系,从而可以运用转化的方法,将求平行四边形的相关问题变成求与圆相关的问题。此外,由于题目较为新颖,担心答案的正确与否时,可以多采用几种方法来计算,以验证答案的准确。
11.×
【解析】
【分析】
周长是围绕圆一周的长度,面积是圆所占平面的大小,两者不是同一单位,无法比较。
【详解】
半径是2厘米的圆,它的周长和面积相等,说法错误。
故答案为:×。
【点睛】
本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积的概念。
12.×
【解析】
【分析】
假设出原来圆的半径,根据和求出圆的周长和面积,最后分析圆的周长和面积的变化情况,据此解答。
【详解】
假设原来圆的半径为3厘米,现在圆的半径为3×=1厘米
原来圆的周长:=(厘米)
现在圆的周长:=(厘米)
÷=
原来圆的面积:=(平方厘米)
现在圆的面积:=(平方厘米)
÷=
所以,一个圆的半径缩小到原来,周长也缩小到原来,面积缩小到原来的。
故答案为:×
【点睛】
一个圆的半径缩小到原来的,周长也缩小到原来的,面积缩小到原来的。
13.×
【解析】
【分析】
小圆和大圆的周长比等于它们的半径比和直径比,小圆和大圆的面积比等于小圆和大圆周长比的平方,据此解答。
【详解】
一个小圆和一个大圆的周长的比为2∶3,那么小圆和大圆面积的比是22∶32=4∶9。
故答案为:×
【点睛】
掌握圆的面积比和周长比的关系是解答题目的关键。
14.√
【解析】
【分析】
空白部分和阴影部分的周长都等于大圆周长的一半与小圆周长的和,空白部分和阴影部分旋转之后完全重合,则空白和阴影两部分面积相等。
【详解】
空白部分的周长:大圆周长的一半+小圆的周长
阴影部分的周长:大圆周长的一半+小圆的周长
空白部分的周长=阴影部分的周长
面积:把空白部分顺时针旋转180°之后与阴影部分完全重合,则空白部分的面积=阴影部分面积=大圆面积的一半。
故答案为:√
【点睛】
掌握图中不规则图形周长的计算方法是解答题目的关键。
15.17.27平方米
【解析】
【分析】
根据半圆面积=πr ÷2,分别求出扩建前后的面积,求差即可。
【详解】
5×2+2
=10+2
=12(米)
12÷2=6(米)
3.14×6 ÷2-3.14×5 ÷2
=56.52-39.25
=17.27(平方米)
答:花坛的面积增加了17.27平方米。
【点睛】
关键是掌握半圆面积求法,半圆面积=圆的面积的一半。
16.分针的尖端所走的路程是157厘米,分针走过的面积是39.25平方厘米。
【解析】
【分析】
从5:00到5:30,分针走的路程是圆周长的一半,分针走过的面积是圆面积的一半,据此解答即可。
【详解】
路程:(厘米)
面积:(平方厘米)
答:分针的尖端所走的路程是157厘米,分针走过的面积是39.25平方厘米。
【点睛】
本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积的计算公式。
17.(1)见详解;
(2)21.5
【解析】
【分析】
(1)连接正方形的对角线交于点O,即为空白圆的圆心;通过圆心并且两端都在圆上的线段叫做直径,直径用字母d表示;
(2)由图可知,正方形的边长为圆的直径,计算出圆的半径,利用求出圆的面积,阴影部分的面积=正方形的面积-圆的面积,据此解答。
【详解】
(1)
(2)10×10-3.14×(10÷2)2
=10×10-3.14×25
=100-78.5
=21.5(平方厘米)
所以,阴影部分的面积是21.5平方厘米。
【点睛】
掌握圆的特征和面积计算公式是解答题目的关键。
18.(1)见详解
(2)30.28厘米,33.72平方厘米
【解析】
【分析】
(1)确定圆心,根据画圆的方法画图半圆,涂色即可;
(2)阴影部分的周长=长方形的长×2+宽+圆周长的一半;阴影部分的面积=长方形面积-半圆面积。
【详解】
(1)画法不唯一
(2)10×2+4+3.14×4÷2
=20+4+6.28
=30.28(厘米)
10×4-3.14×(4÷2) ÷2
=40-3.14×4÷2
=40-6.28
=33.72(平方厘米)
答:阴影部分的周长是30.28厘米,面积是33.72平方厘米。
【点睛】
关键是掌握画圆的方法,掌握圆的周长和面积公式。
19.56.52平方米;20.41平方米
【解析】
【分析】
(1)由题意可知,半圆的周长为18.84米,利用圆的周长公式计算出圆的半径,再根据求出鸡舍的面积;
(2)大圆的半径=小圆的半径+环宽,利用圆环的面积公式:,即可求得。
【详解】
(1)半径:18.84×2÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
面积:3.14×62÷2
=3.14×36÷2
=113.04÷2
=56.52(平方米)
答:这个鸡舍的面积是56.52平方米。
(2)3.14×[(6+1)2-62]÷2
=3.14×[49-36]÷2
=3.14×13÷2
=40.82÷2
=20.41(平方米)
答:鸡舍面积扩大了20.41平方米。
【点睛】
掌握圆的周长和面积以及圆环的面积计算公式是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.用同样长的铁丝,分别围成长方形、正方形、三角形、圆,( )的面积最大。
A.圆 B.长方形 C.正方形 D.三角形
2.把一个圆平均分成32份,然后剪开,拼成一个近似的长方形,这个转化过程中( )。
A.周长、面积都没变 B.周长没变,面积变了 C.周长变了,面积没变 D.周长、面积都变了
3.在一个正方形内画一个最大的圆,这个圆的面积是正方形面积的( )。
A. B. C. D.
4.大圆和小圆的周长比是7∶4,那么小圆和大圆的面积比是( )。
A.49∶16 B.14∶8 C.16∶49 D.8∶14
5.以大圆的半径为直径画一个小圆,大圆与小圆的面积的比值是( )。
A.4 B.0.25 C.2 D.5
6.下列三个图形,阴影部分的面积相比,( )。
① ② ③
A.①>②>③ B.②>①>③ C.一样大
二、填空题
7.在长是20厘米,宽8厘米的长方形中剪一个最大的半圆,这个半圆的直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
8.一个圆的周长、半径、直径的和是55.68cm,这个圆的面积是( )。
9.一个时钟的分针长15厘米,分针绕钟面走一圈,分针的尖端所走过的路程是( )厘米,它所扫过的平面的面积是( )平方厘米。
10.借助推导圆面积公式时所使用的方法,小芳在研究圆环的面积时,把圆环等分成16份,拼成一个近似的平行四边形(如图)。如果圆环的内圆半径是2cm,外圆半径是6cm,拼成的近似平行四边形的底边长约为( )cm,则圆环的面积为( )cm2。
三、判断题
11.半径是2厘米的圆,它的周长和面积相等。( )
12.一个圆的半径缩小到原来,周长和面积也缩小到原来的。( )
13.一个小圆和一个大圆的周长的比为2∶3,那么小圆和大圆面积的比也是2∶3。( )
14.图中阴影部分与空白部分的周长相等,面积也相等。( )
四、解答题
15.人民广场有一个半径是5m的半圆形花坛。如果要扩建这个花坛,把它的直径增加2m,花坛的面积增加了多少?
16.教室的钟表分针长10cm,从5:00到5:30,分针的尖端所走的路程是多少厘米?分针走过的面积是多少平方厘米?
17.(1)请你找出下面圆的圆心和直径,并用字母标注出来。
(2)上图中的正方形边长为10厘米,阴影部分的面积是( )平方厘米。
18.(1)以下图长方形的宽为直径在长方形内画一个半圆,并将图形的其他部分(即半圆以外的部分)画上阴影。
(2)分别求阴影部分的周长和面积。
19.爷爷用18.84m长的篱笆靠墙围了一个半圆形的鸡舍。这个鸡舍的面积是多少平方米?爷爷觉得鸡舍面积小,又沿着篱笆外围拓宽了1米,鸡舍面积扩大了多少平方米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
根据长方形、正方形、三角形、圆的周长一定,圆的面积最大进行选择。
【详解】
用同样长的铁丝,说明周长一定,分别围成长方形、正方形、三角形、圆,圆的面积最大。
故答案为:A
【点睛】
有些结论记下来可以节省大量思考和解题时间。
2.C
【解析】
【分析】
如图
当圆被平均分为很多份时,长方形的面积十分接近圆的面积。圆的面积=长方形的面积=长×宽=πr×r=πr ,而长方形的周长比圆的周长多了两条半径。
【详解】
把一个圆平均分成32份,然后剪开,拼成一个近似的长方形,这个转化过程中周长变了,面积没变。
故答案为:C
【点睛】
关键是熟悉圆的面积公式推导过程。
3.D
【解析】
【分析】
正方形内最大的圆的直径等于正方形的边长,可设圆的半径为r,则圆的直径为2r,正方形的边长为2r,由此利用圆的面积公式和正方形的面积公式即可解答。
【详解】
设圆的半径为r,则圆的直径为2r,正方形的边长为2r,
圆的面积:πr2
正方形的面积:2r×2r=4r2
πr2÷4r2=
这个圆的面积是正方形面积的。
故选:D。
【点睛】
此题主要考查的是正方形面积公式和圆的面积公式的灵活应用。
4.A
【解析】
【分析】
根据周长比的平方是面积比,进行分析。
【详解】
7 ∶4 =49∶16
故答案为:A
【点睛】
圆的面积=πr ,两数相除又叫两个数的比。
5.A
【解析】
【分析】
假设大圆的半径是2厘米,那么小圆的直径是2厘米。据此结合圆的面积公式,先分别求出大圆和小圆的面积,从而做比求出比值,选出正确选项。
【详解】
令大圆半径是2厘米,那么小圆直径是2厘米,小圆半径是1厘米。
大圆面积:3.14×22=12.56(平方厘米)
小圆面积:3.14×12=3.14(平方厘米)
12.56∶3.14=12.56÷3.14=4
所以,大圆和小圆的面积的比值是4。
故答案为:A
【点睛】
本题考查了圆的面积,灵活运用圆的面积公式是解题的关键。
6.C
【解析】
【分析】
图①圆的直径等于正方形的边长,阴影部分的面积=正方形的面积-圆的面积;
图②空白部分的两个半圆可以拼成一个圆,直径等于正方形的边长,阴影部分的面积=正方形的面积-圆的面积;
图③空白部分的四个扇形可以拼成一个圆,直径等于正方形的边长,阴影部分的面积=正方形的面积-圆的面积;
拼成的圆的面积相等,正方形的面积也相等,所以阴影部分的面积也相等,据此解答即可。
【详解】
图②和图③的空白部分可以在组成和图①空白部分相等的圆,正方形的面积也相等,所以三个图中阴影部分的面积也相等;
故答案为:C。
【点睛】
解答本题的关键要注意观察图形,确定每个图形阴影部分的面积如何计算。
7. 16 41.12 100.48
【解析】
【分析】
在长是20厘米,宽8厘米的长方形中剪一个最大的半圆,半圆的半径=长方形的宽,半径×2=直径,根据半圆的周长=πr+2r,半圆的面积=πr ÷2,计算即可。
【详解】
8×2=16(厘米)
3.14×8+16
=25.12+16
=41.12(厘米)
3.14×8 ÷2=100.48(平方厘米)
【点睛】
关键是掌握半圆的周长和面积公式。
8.113.04平方厘米
【解析】
【分析】
设半径是x厘米,则直径是2x厘米,周长是2×3.14x厘米,根据半径+直径+周长=55.68厘米,列出方程求出x的值是半径,根据圆的面积=πr ,计算即可。
【详解】
解:设半径是x厘米。
x+2x+2×3.14x=55.68
3x+6.28x=55.68
9.28x÷9.28=55.68÷9.28
x=6
3.14×6 =113.04(平方厘米)
【点睛】
关键是掌握圆的周长和面积公式。
9. 94.2 706.5
【解析】
【分析】
已知这个时钟的分针长15厘米,因为若把钟面看作一个圆,则时针相当于半径,所以要计算分针绕钟面走一圈,分针尖端所走过的路程、扫过的面积就是求圆的周长、面积。可套用公式来解答。
【详解】
C圆=2πr
=2×3.14×15
=3.14×30
=94.2(厘米)
S圆=πr2
=3.14×152
=3.14×225
=706.5(平方厘米)
【点睛】
本题需要我们展开空间思维,想象钟面及钟面上分针尖端走一圈的的样子,从而联想起圆的周长、面积计算方法,并通过相关公式来计算。
10. 25.12 100.48
【解析】
【分析】
①由题意:将一个圆环剪开,拼成一个近似的平行四边形。如果把圆环所被平均分成的每一份看作一个近似的梯形,则拼成的平行四边形的底就是由梯形的上底和下底穿插着组成的。而梯形的下底实际上是小圆周长的每一份,因此可得出:平行四边形的底边就是大圆周长与小圆周长之和的一半,可列式:(2×3.14×6+2×3.14×2)÷2=25.12(cm);
②要计算圆环的面积,有两种方法:可以通过圆环面积公式来列式;还可以转化为求平行四边形的面积来列式:25.12×(6-2)=100.48(cm2)
【详解】
①(2×3.14×6+2×3.14×2)÷2
=(3.14×12+3.14×4)÷2
=50.24÷2
=25.12(cm)
②3.14×(62-22)
=3.14×(36-4)
=3.14×32
=100.48(cm2)
25.12×(6-2)
=25.12×4
=100.48(cm2)
【点睛】
解答本题,在充分理解题意的同时,更要仔细读图。只有细致的观察图形,才能够找出圆环与平行四边形之间的联系,从而可以运用转化的方法,将求平行四边形的相关问题变成求与圆相关的问题。此外,由于题目较为新颖,担心答案的正确与否时,可以多采用几种方法来计算,以验证答案的准确。
11.×
【解析】
【分析】
周长是围绕圆一周的长度,面积是圆所占平面的大小,两者不是同一单位,无法比较。
【详解】
半径是2厘米的圆,它的周长和面积相等,说法错误。
故答案为:×。
【点睛】
本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积的概念。
12.×
【解析】
【分析】
假设出原来圆的半径,根据和求出圆的周长和面积,最后分析圆的周长和面积的变化情况,据此解答。
【详解】
假设原来圆的半径为3厘米,现在圆的半径为3×=1厘米
原来圆的周长:=(厘米)
现在圆的周长:=(厘米)
÷=
原来圆的面积:=(平方厘米)
现在圆的面积:=(平方厘米)
÷=
所以,一个圆的半径缩小到原来,周长也缩小到原来,面积缩小到原来的。
故答案为:×
【点睛】
一个圆的半径缩小到原来的,周长也缩小到原来的,面积缩小到原来的。
13.×
【解析】
【分析】
小圆和大圆的周长比等于它们的半径比和直径比,小圆和大圆的面积比等于小圆和大圆周长比的平方,据此解答。
【详解】
一个小圆和一个大圆的周长的比为2∶3,那么小圆和大圆面积的比是22∶32=4∶9。
故答案为:×
【点睛】
掌握圆的面积比和周长比的关系是解答题目的关键。
14.√
【解析】
【分析】
空白部分和阴影部分的周长都等于大圆周长的一半与小圆周长的和,空白部分和阴影部分旋转之后完全重合,则空白和阴影两部分面积相等。
【详解】
空白部分的周长:大圆周长的一半+小圆的周长
阴影部分的周长:大圆周长的一半+小圆的周长
空白部分的周长=阴影部分的周长
面积:把空白部分顺时针旋转180°之后与阴影部分完全重合,则空白部分的面积=阴影部分面积=大圆面积的一半。
故答案为:√
【点睛】
掌握图中不规则图形周长的计算方法是解答题目的关键。
15.17.27平方米
【解析】
【分析】
根据半圆面积=πr ÷2,分别求出扩建前后的面积,求差即可。
【详解】
5×2+2
=10+2
=12(米)
12÷2=6(米)
3.14×6 ÷2-3.14×5 ÷2
=56.52-39.25
=17.27(平方米)
答:花坛的面积增加了17.27平方米。
【点睛】
关键是掌握半圆面积求法,半圆面积=圆的面积的一半。
16.分针的尖端所走的路程是157厘米,分针走过的面积是39.25平方厘米。
【解析】
【分析】
从5:00到5:30,分针走的路程是圆周长的一半,分针走过的面积是圆面积的一半,据此解答即可。
【详解】
路程:(厘米)
面积:(平方厘米)
答:分针的尖端所走的路程是157厘米,分针走过的面积是39.25平方厘米。
【点睛】
本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积的计算公式。
17.(1)见详解;
(2)21.5
【解析】
【分析】
(1)连接正方形的对角线交于点O,即为空白圆的圆心;通过圆心并且两端都在圆上的线段叫做直径,直径用字母d表示;
(2)由图可知,正方形的边长为圆的直径,计算出圆的半径,利用求出圆的面积,阴影部分的面积=正方形的面积-圆的面积,据此解答。
【详解】
(1)
(2)10×10-3.14×(10÷2)2
=10×10-3.14×25
=100-78.5
=21.5(平方厘米)
所以,阴影部分的面积是21.5平方厘米。
【点睛】
掌握圆的特征和面积计算公式是解答题目的关键。
18.(1)见详解
(2)30.28厘米,33.72平方厘米
【解析】
【分析】
(1)确定圆心,根据画圆的方法画图半圆,涂色即可;
(2)阴影部分的周长=长方形的长×2+宽+圆周长的一半;阴影部分的面积=长方形面积-半圆面积。
【详解】
(1)画法不唯一
(2)10×2+4+3.14×4÷2
=20+4+6.28
=30.28(厘米)
10×4-3.14×(4÷2) ÷2
=40-3.14×4÷2
=40-6.28
=33.72(平方厘米)
答:阴影部分的周长是30.28厘米,面积是33.72平方厘米。
【点睛】
关键是掌握画圆的方法,掌握圆的周长和面积公式。
19.56.52平方米;20.41平方米
【解析】
【分析】
(1)由题意可知,半圆的周长为18.84米,利用圆的周长公式计算出圆的半径,再根据求出鸡舍的面积;
(2)大圆的半径=小圆的半径+环宽,利用圆环的面积公式:,即可求得。
【详解】
(1)半径:18.84×2÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
面积:3.14×62÷2
=3.14×36÷2
=113.04÷2
=56.52(平方米)
答:这个鸡舍的面积是56.52平方米。
(2)3.14×[(6+1)2-62]÷2
=3.14×[49-36]÷2
=3.14×13÷2
=40.82÷2
=20.41(平方米)
答:鸡舍面积扩大了20.41平方米。
【点睛】
掌握圆的周长和面积以及圆环的面积计算公式是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
