人教版六年级上册5.4扇形同步练习(含答案)
文档属性
| 名称 | 人教版六年级上册5.4扇形同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 110.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览



文档简介
人教版六年级上册 5.4 扇形 同步练习
一、选择题
1.一条弧和经过这条弧两端的两条半径所围成图形叫做( )。
A.圆心角 B.扇形 C.弧形
2.在同一个圆中,扇形的大小与( )的大小有关。
A.这个扇形的圆心角 B.这个圆的半径 C.这个圆的直径
3.下面各图中,阴影部分是扇形的是( )。
A.
B.
C.
D.
4.在一个圆中,以圆为弧的扇形的圆心角是( )。
A.360度 B.180度 C.90度 D.45度
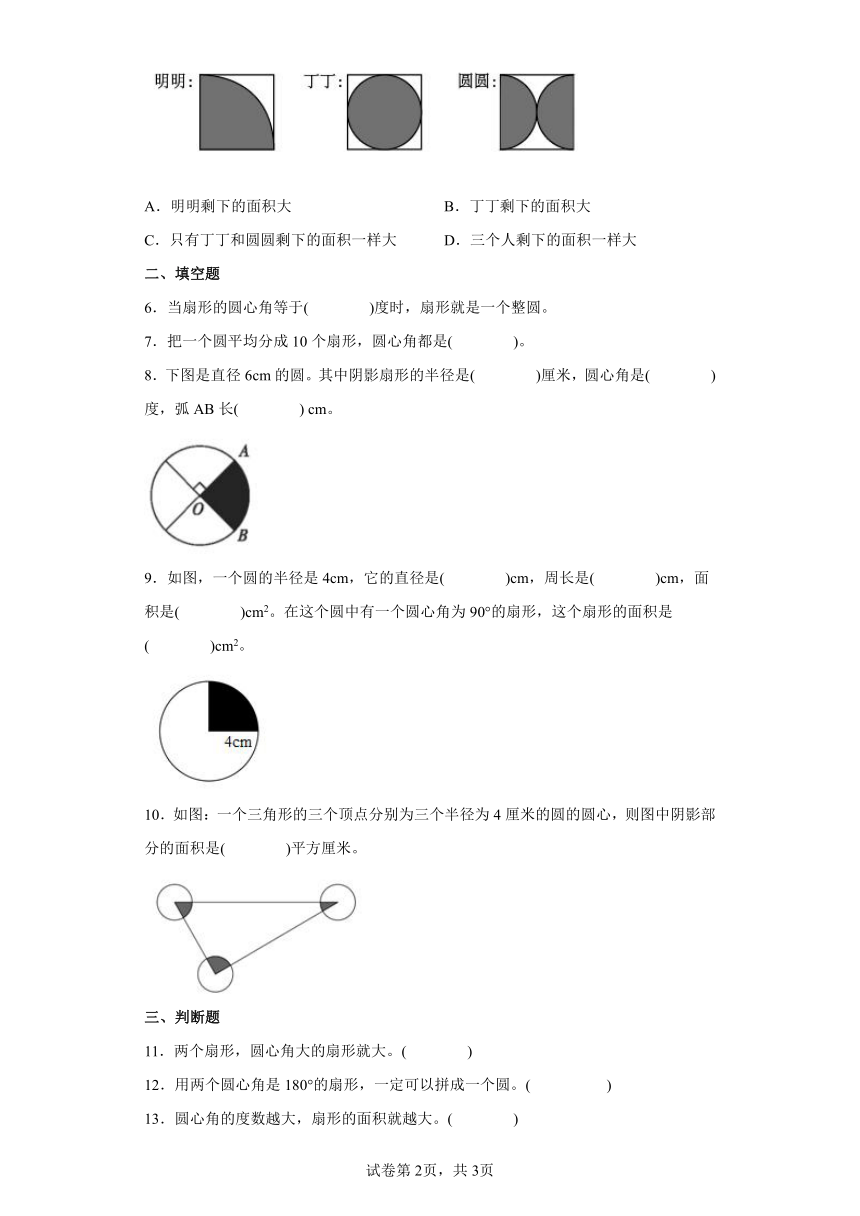
5.明明、丁丁、圆圆分别从同样大的正方形中剪掉了涂色部分的图形(如下图),他们剩下部分的面积相比,( )。
A.明明剩下的面积大 B.丁丁剩下的面积大
C.只有丁丁和圆圆剩下的面积一样大 D.三个人剩下的面积一样大
二、填空题
6.当扇形的圆心角等于( )度时,扇形就是一个整圆。
7.把一个圆平均分成10个扇形,圆心角都是( )。
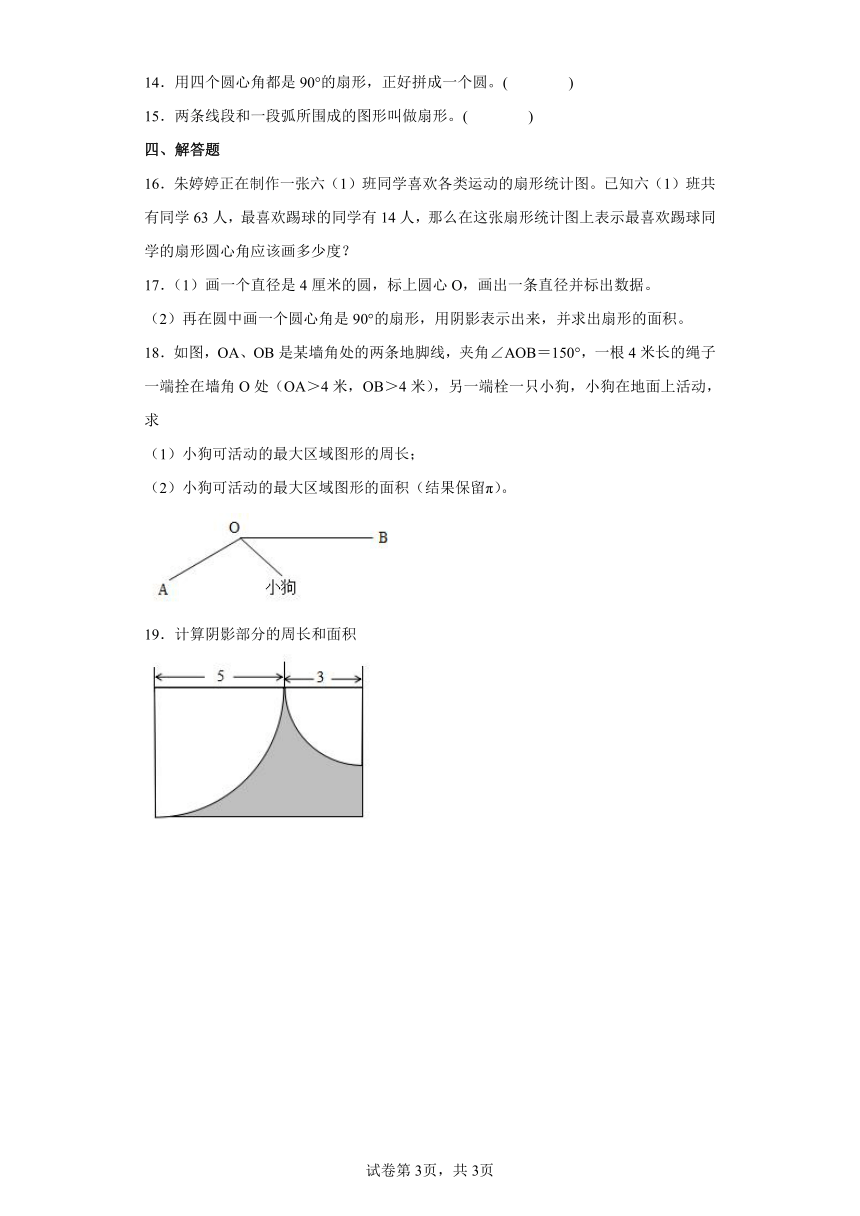
8.下图是直径6cm的圆。其中阴影扇形的半径是( )厘米,圆心角是( )度,弧AB长( ) cm。
9.如图,一个圆的半径是4cm,它的直径是( )cm,周长是( )cm,面积是( )cm2。在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是( )cm2。
10.如图:一个三角形的三个顶点分别为三个半径为4厘米的圆的圆心,则图中阴影部分的面积是( )平方厘米。
三、判断题
11.两个扇形,圆心角大的扇形就大。( )
12.用两个圆心角是180°的扇形,一定可以拼成一个圆。( )
13.圆心角的度数越大,扇形的面积就越大。( )
14.用四个圆心角都是90°的扇形,正好拼成一个圆。( )
15.两条线段和一段弧所围成的图形叫做扇形。( )
四、解答题
16.朱婷婷正在制作一张六(1)班同学喜欢各类运动的扇形统计图。已知六(1)班共有同学63人,最喜欢踢球的同学有14人,那么在这张扇形统计图上表示最喜欢踢球同学的扇形圆心角应该画多少度?
17.(1)画一个直径是4厘米的圆,标上圆心O,画出一条直径并标出数据。
(2)再在圆中画一个圆心角是90°的扇形,用阴影表示出来,并求出扇形的面积。
18.如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求
(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π)。
19.计算阴影部分的周长和面积
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
一条弧和经过这条弧两端的两条半径所围成图形叫做扇形,图中涂色部分就是扇形。
故答案为:B
2.A
【解析】
【分析】
由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形,据此分析。
【详解】
在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
故答案为:A
【点睛】
扇形是圆的一部分。
3.A
【解析】
【分析】
一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,由此可知,它是由圆周的一部分与它所对应的圆心围成的,据此选择。
【详解】
根据扇形的概念可知,的阴影部分是扇形。
故选择:A
【点睛】
此题考查了扇形的概念,掌握扇形特点解答即可。
4.C
【解析】
【分析】
整个圆对应的圆心角是360°,求圆弧对应的圆心角,用360°×即可。
【详解】
360°×=90°。
故选择:C
【点睛】
此题考查了圆心角的相关计算。
5.D
【解析】
【分析】
这是三个同样大的正方形,可假设正方形的边长是2,分别算出明明、丁丁、圆圆剪掉涂色部分的面积,涂色部分面积越大的剩下部分的面积越小,涂色部分面积越小的剩下部分的面积越大,据此作出选择即可。
【详解】
假设正方形的边长是2。
明明:×(2×2×π)
=×4×π
=π
丁丁:1×1×π
=1×π
=π
圆圆:1×1×π
=1×π
=π
三个人的涂色部分面积相等,即三个人剩下的面积一样大。
故答案选:D
【点睛】
掌握扇形、圆的面积计算方法,这是解决此题的关键。
6.360
【解析】
【分析】
在同一个圆内,扇形的大小与这个扇形的圆心角的大小有关,因为圆的圆心角为360°,所以当扇形的圆心角等于360度时,扇形就是一个整圆。
【详解】
由分析得,
当扇形的圆心角等于360度时,扇形就是一个整圆。
【点睛】
此题考查的是圆和扇形的关系,掌握在同一个圆内,扇形的大小与这个扇形的圆心角的大小有关是解题关键。
7.36°
【解析】
【分析】
一个周角是360°,360°平均分成10份,求每份是多少用除法计算即可。
【详解】
360°÷10=36°
【点睛】
掌握扇形圆心角的意义是解答题目的关键。
8. 3 90 4.71
【解析】
【分析】
根据半径=直径÷2即可求出半径;根据图意可知把圆平均分成4份,每份的圆心角是360÷4=90°;弧AB长是圆周长的,据此解答。
【详解】
由分析得,
直径6cm的圆。其中阴影扇形的半径是3厘米,圆心角是360÷4=90°,
弧AB长:
3.14×6×
=18.84×
=4.71(厘米)
【点睛】
此题考查的是同心圆中扇形与圆的关系,明确弧AB长是圆周长的是解题关键。
9. 8 25.12 50.24 12.56
【解析】
【分析】
根据同一个圆直径等于半径的2倍,根据圆的周长公式C=πd,圆的面积公式S=πr2,在这个圆中有一个圆心角为90°的扇形,这个扇形的面积等于整圆面积的。据此解答即可。
【详解】
4×2=8(cm)
3.14×8=25.12(cm)
3.14×42=50.24(平方厘米)
50.24×=12.56(平方厘米)
则它的直径是8cm,周长是25.12cm,面积是50.24cm2。在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是12.56cm2。
【点睛】
本题考查圆的周长和面积,熟记公式是解题的关键。
10.25.12
【解析】
【分析】
三角形的内角和是180°,所以三个扇形阴影部分的圆心角的度数和也是180°,那么阴影部分的面积就恰好是半径为4厘米的圆的面积的一半。据此解题。
【详解】
3.14×42÷2
=3.14×16÷2
=25.12(平方厘米)
所以,阴影部分的面积是25.12平方厘米。
【点睛】
本题考查了半圆的面积,半圆的面积等于对应圆的面积除以2。
11.×
【解析】
【分析】
扇形的大小与所在圆的半径和圆心角的大小有关,据此解答。
【详解】
由分析得,
扇形的大小既要考虑圆心角的大小还要考虑所在圆的半径的大小。
故答案:×
【点睛】
此题考查的是扇形特点,掌握扇形的大小与所在圆的半径和圆心角的大小有关是解题关键。
12.×
【解析】
【分析】
两个圆心角是180°的扇形,半径不一定相等,当两个扇形的半径相等时,可以拼成一个圆;当两个扇形的半径不相等时,不可以拼成一个圆。
【详解】
用两个圆心角是180°且半径相等的扇形,一定可以拼成一个圆。
故答案为:×
【点睛】
掌握扇形的特征是解答题目的关键。
13.×
【解析】
【分析】
在同圆或等圆中,圆心角越大所对应的弧线越长,得到的扇形的面积越大,圆心角越小所对应的弧线越短,扇形的面积越小,据此判断即可。
【详解】
在同圆或等圆中,圆心角的度数越大,扇形的面积就越大,原题说法错误;
故答案为:×。
【点睛】
熟练掌握有关圆心角的基础知识是解答本题的关键。
14.×
【解析】
【分析】
用4个圆心角都是90°的扇形不一定可以拼成一个圆,因为扇形的半径不一定相等.据此解答。
【详解】
4个圆心角都是90°的扇形,半径不一定相等,所以用4个圆心角都是90°的扇形不一定可以拼成一个圆。故原题干说法错误。
【点睛】
本题主要考查了半径决定圆的大小。
15.×
【解析】
【分析】
根据扇形的意义:由两条半径,和连接两条半径的一段弧围成的图形叫做扇形,据此解答。
【详解】
由分析可知:
由两条半径和连接两条半径的一段弧围成的图形叫做扇形。故原题干说法错误。
【点睛】
此题考查扇形的意义,掌握基本概念解决问题。
16.80度
【解析】
【分析】
根据分数意义求出踢球同学人数占总人数的分率,再用分率乘扇形圆心角360°即可得到踢球的同学的扇形圆心角的度数。
【详解】
14÷63×360°
=×360°
=80°
答:那么在这张扇形统计图上表示最喜欢踢球同学的扇形圆心角应该画80度。
【点睛】
此题考查的是扇形统计图的圆心角度数的计算,根据题意求出踢球同学人数占总人数的分率是解题关键。
17.作图见详解;
3.14平方厘米
【解析】
【分析】
(1)画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(2)由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。扇形面积=πr ×。
【详解】
3.14×(4÷2) ×
=3.14×4×
=3.14(平方厘米)
答:扇形的面积是3.14平方厘米。
【点睛】
关键是掌握画圆的方法,掌握扇形面积公式。
18.(1)米;(2)平方米
【解析】
【分析】
(1)根据题意可知,小狗活动的区域为一个扇形,圆心角为150°,半径为绳长4米,根据弧长公式:π×半径×2×,代入数据,即可解答。
(2)小狗活动区域就是圆心角150°的扇形面积,根据扇形面积公式:π×半径2×,代入数据,即可解答。
【详解】
(1)π×4×2×
=8π×
= (米)
答:小狗可活动的区域图形的周长是米。
(2)π×42×
=π×16×
=(平方米)
答:小狗可活动的最大区域图形的面积平方米。
【点睛】
本题考查了扇形面积和弧长的计算在实际问题中的运用。熟记公式是解题的关键。
19.22.56;13.31
【解析】
【分析】
由图形可知,阴影部分的周长指的是阴影部分一周的长度。即两个扇形的弧长+长方形的长+两个扇形半径的差;阴影部分的面积=长方形的面积-两个扇形的面积,据此可解答。
【详解】
两个扇形的弧长:×(3.14×5×2+3.14×3×2)
=×(31.4+18.84)
=×50.24
=12.56
阴影部分的周长:12.56+(5+3)+(5-3)
=12.56+8+2
=22.56
长方形的面积:(5+3)×5
=8×5
=40
两个扇形的面积:×(3.14×52+3.14×32)
=×(78.5+28.26)
=×106.76
=26.69
40-26.69=13.31
【点睛】
本题考查扇形的面积和弧长,明确扇形的面积和弧长的计算方法是解题的关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.一条弧和经过这条弧两端的两条半径所围成图形叫做( )。
A.圆心角 B.扇形 C.弧形
2.在同一个圆中,扇形的大小与( )的大小有关。
A.这个扇形的圆心角 B.这个圆的半径 C.这个圆的直径
3.下面各图中,阴影部分是扇形的是( )。
A.
B.
C.
D.
4.在一个圆中,以圆为弧的扇形的圆心角是( )。
A.360度 B.180度 C.90度 D.45度
5.明明、丁丁、圆圆分别从同样大的正方形中剪掉了涂色部分的图形(如下图),他们剩下部分的面积相比,( )。
A.明明剩下的面积大 B.丁丁剩下的面积大
C.只有丁丁和圆圆剩下的面积一样大 D.三个人剩下的面积一样大
二、填空题
6.当扇形的圆心角等于( )度时,扇形就是一个整圆。
7.把一个圆平均分成10个扇形,圆心角都是( )。
8.下图是直径6cm的圆。其中阴影扇形的半径是( )厘米,圆心角是( )度,弧AB长( ) cm。
9.如图,一个圆的半径是4cm,它的直径是( )cm,周长是( )cm,面积是( )cm2。在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是( )cm2。
10.如图:一个三角形的三个顶点分别为三个半径为4厘米的圆的圆心,则图中阴影部分的面积是( )平方厘米。
三、判断题
11.两个扇形,圆心角大的扇形就大。( )
12.用两个圆心角是180°的扇形,一定可以拼成一个圆。( )
13.圆心角的度数越大,扇形的面积就越大。( )
14.用四个圆心角都是90°的扇形,正好拼成一个圆。( )
15.两条线段和一段弧所围成的图形叫做扇形。( )
四、解答题
16.朱婷婷正在制作一张六(1)班同学喜欢各类运动的扇形统计图。已知六(1)班共有同学63人,最喜欢踢球的同学有14人,那么在这张扇形统计图上表示最喜欢踢球同学的扇形圆心角应该画多少度?
17.(1)画一个直径是4厘米的圆,标上圆心O,画出一条直径并标出数据。
(2)再在圆中画一个圆心角是90°的扇形,用阴影表示出来,并求出扇形的面积。
18.如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求
(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π)。
19.计算阴影部分的周长和面积
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
一条弧和经过这条弧两端的两条半径所围成图形叫做扇形,图中涂色部分就是扇形。
故答案为:B
2.A
【解析】
【分析】
由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形,据此分析。
【详解】
在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
故答案为:A
【点睛】
扇形是圆的一部分。
3.A
【解析】
【分析】
一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,由此可知,它是由圆周的一部分与它所对应的圆心围成的,据此选择。
【详解】
根据扇形的概念可知,的阴影部分是扇形。
故选择:A
【点睛】
此题考查了扇形的概念,掌握扇形特点解答即可。
4.C
【解析】
【分析】
整个圆对应的圆心角是360°,求圆弧对应的圆心角,用360°×即可。
【详解】
360°×=90°。
故选择:C
【点睛】
此题考查了圆心角的相关计算。
5.D
【解析】
【分析】
这是三个同样大的正方形,可假设正方形的边长是2,分别算出明明、丁丁、圆圆剪掉涂色部分的面积,涂色部分面积越大的剩下部分的面积越小,涂色部分面积越小的剩下部分的面积越大,据此作出选择即可。
【详解】
假设正方形的边长是2。
明明:×(2×2×π)
=×4×π
=π
丁丁:1×1×π
=1×π
=π
圆圆:1×1×π
=1×π
=π
三个人的涂色部分面积相等,即三个人剩下的面积一样大。
故答案选:D
【点睛】
掌握扇形、圆的面积计算方法,这是解决此题的关键。
6.360
【解析】
【分析】
在同一个圆内,扇形的大小与这个扇形的圆心角的大小有关,因为圆的圆心角为360°,所以当扇形的圆心角等于360度时,扇形就是一个整圆。
【详解】
由分析得,
当扇形的圆心角等于360度时,扇形就是一个整圆。
【点睛】
此题考查的是圆和扇形的关系,掌握在同一个圆内,扇形的大小与这个扇形的圆心角的大小有关是解题关键。
7.36°
【解析】
【分析】
一个周角是360°,360°平均分成10份,求每份是多少用除法计算即可。
【详解】
360°÷10=36°
【点睛】
掌握扇形圆心角的意义是解答题目的关键。
8. 3 90 4.71
【解析】
【分析】
根据半径=直径÷2即可求出半径;根据图意可知把圆平均分成4份,每份的圆心角是360÷4=90°;弧AB长是圆周长的,据此解答。
【详解】
由分析得,
直径6cm的圆。其中阴影扇形的半径是3厘米,圆心角是360÷4=90°,
弧AB长:
3.14×6×
=18.84×
=4.71(厘米)
【点睛】
此题考查的是同心圆中扇形与圆的关系,明确弧AB长是圆周长的是解题关键。
9. 8 25.12 50.24 12.56
【解析】
【分析】
根据同一个圆直径等于半径的2倍,根据圆的周长公式C=πd,圆的面积公式S=πr2,在这个圆中有一个圆心角为90°的扇形,这个扇形的面积等于整圆面积的。据此解答即可。
【详解】
4×2=8(cm)
3.14×8=25.12(cm)
3.14×42=50.24(平方厘米)
50.24×=12.56(平方厘米)
则它的直径是8cm,周长是25.12cm,面积是50.24cm2。在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是12.56cm2。
【点睛】
本题考查圆的周长和面积,熟记公式是解题的关键。
10.25.12
【解析】
【分析】
三角形的内角和是180°,所以三个扇形阴影部分的圆心角的度数和也是180°,那么阴影部分的面积就恰好是半径为4厘米的圆的面积的一半。据此解题。
【详解】
3.14×42÷2
=3.14×16÷2
=25.12(平方厘米)
所以,阴影部分的面积是25.12平方厘米。
【点睛】
本题考查了半圆的面积,半圆的面积等于对应圆的面积除以2。
11.×
【解析】
【分析】
扇形的大小与所在圆的半径和圆心角的大小有关,据此解答。
【详解】
由分析得,
扇形的大小既要考虑圆心角的大小还要考虑所在圆的半径的大小。
故答案:×
【点睛】
此题考查的是扇形特点,掌握扇形的大小与所在圆的半径和圆心角的大小有关是解题关键。
12.×
【解析】
【分析】
两个圆心角是180°的扇形,半径不一定相等,当两个扇形的半径相等时,可以拼成一个圆;当两个扇形的半径不相等时,不可以拼成一个圆。
【详解】
用两个圆心角是180°且半径相等的扇形,一定可以拼成一个圆。
故答案为:×
【点睛】
掌握扇形的特征是解答题目的关键。
13.×
【解析】
【分析】
在同圆或等圆中,圆心角越大所对应的弧线越长,得到的扇形的面积越大,圆心角越小所对应的弧线越短,扇形的面积越小,据此判断即可。
【详解】
在同圆或等圆中,圆心角的度数越大,扇形的面积就越大,原题说法错误;
故答案为:×。
【点睛】
熟练掌握有关圆心角的基础知识是解答本题的关键。
14.×
【解析】
【分析】
用4个圆心角都是90°的扇形不一定可以拼成一个圆,因为扇形的半径不一定相等.据此解答。
【详解】
4个圆心角都是90°的扇形,半径不一定相等,所以用4个圆心角都是90°的扇形不一定可以拼成一个圆。故原题干说法错误。
【点睛】
本题主要考查了半径决定圆的大小。
15.×
【解析】
【分析】
根据扇形的意义:由两条半径,和连接两条半径的一段弧围成的图形叫做扇形,据此解答。
【详解】
由分析可知:
由两条半径和连接两条半径的一段弧围成的图形叫做扇形。故原题干说法错误。
【点睛】
此题考查扇形的意义,掌握基本概念解决问题。
16.80度
【解析】
【分析】
根据分数意义求出踢球同学人数占总人数的分率,再用分率乘扇形圆心角360°即可得到踢球的同学的扇形圆心角的度数。
【详解】
14÷63×360°
=×360°
=80°
答:那么在这张扇形统计图上表示最喜欢踢球同学的扇形圆心角应该画80度。
【点睛】
此题考查的是扇形统计图的圆心角度数的计算,根据题意求出踢球同学人数占总人数的分率是解题关键。
17.作图见详解;
3.14平方厘米
【解析】
【分析】
(1)画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(2)由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。扇形面积=πr ×。
【详解】
3.14×(4÷2) ×
=3.14×4×
=3.14(平方厘米)
答:扇形的面积是3.14平方厘米。
【点睛】
关键是掌握画圆的方法,掌握扇形面积公式。
18.(1)米;(2)平方米
【解析】
【分析】
(1)根据题意可知,小狗活动的区域为一个扇形,圆心角为150°,半径为绳长4米,根据弧长公式:π×半径×2×,代入数据,即可解答。
(2)小狗活动区域就是圆心角150°的扇形面积,根据扇形面积公式:π×半径2×,代入数据,即可解答。
【详解】
(1)π×4×2×
=8π×
= (米)
答:小狗可活动的区域图形的周长是米。
(2)π×42×
=π×16×
=(平方米)
答:小狗可活动的最大区域图形的面积平方米。
【点睛】
本题考查了扇形面积和弧长的计算在实际问题中的运用。熟记公式是解题的关键。
19.22.56;13.31
【解析】
【分析】
由图形可知,阴影部分的周长指的是阴影部分一周的长度。即两个扇形的弧长+长方形的长+两个扇形半径的差;阴影部分的面积=长方形的面积-两个扇形的面积,据此可解答。
【详解】
两个扇形的弧长:×(3.14×5×2+3.14×3×2)
=×(31.4+18.84)
=×50.24
=12.56
阴影部分的周长:12.56+(5+3)+(5-3)
=12.56+8+2
=22.56
长方形的面积:(5+3)×5
=8×5
=40
两个扇形的面积:×(3.14×52+3.14×32)
=×(78.5+28.26)
=×106.76
=26.69
40-26.69=13.31
【点睛】
本题考查扇形的面积和弧长,明确扇形的面积和弧长的计算方法是解题的关键。
答案第1页,共2页
答案第1页,共2页
