2021-2022学年湘教版七年级数学下册2.2.2完全平方公式同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版七年级数学下册2.2.2完全平方公式同步达标测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 78.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 20:04:35 | ||
图片预览



文档简介
2021-2022学年湘教版七年级数学下册《2-2-2完全平方公式》同步达标测试题(附答案)
一.选择题(共6小题,满分30分)
1.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
2.已知a﹣b=2,a2+b2=20,则ab值是( )
A.﹣8 B.12 C.8 D.9
3.已知(x﹣1)2=2,则代数式x2﹣2x+5的值为( )
A.4 B.5 C.6 D.7
4.若x2+(a﹣1)x+25是一个完全平方式,则a值为( )
A.﹣9 B.﹣9或11 C.9或﹣11 D.11
5.若a+b=﹣2,ab=3,则代数式a2﹣ab+b2的值是( )
A.﹣5 B.13 C.5 D.9
6.已知(2022﹣x)(2020﹣x)=2021,那么(2022﹣x)2+(2020﹣x)2的值是( )
A.20212 B.4042 C.4046 D.2021
二.填空题(共7小题,满分35分)
7.若(x+y)2=8,xy=3,则x2+y2= .
8.已知a+b=10,ab=﹣5,则a2+b2= .
9.已知(x﹣2019)2+(x﹣2021)2=48,则(x﹣2020)2= .
10.当a= 时,多项式x2﹣2(a﹣1)x+25是一个完全平方式.
11.如图,已知正方形ABCD与正方形CEFG的边长分别为a、b,如果a+b=10,ab=8,则阴影部分的面积为 .
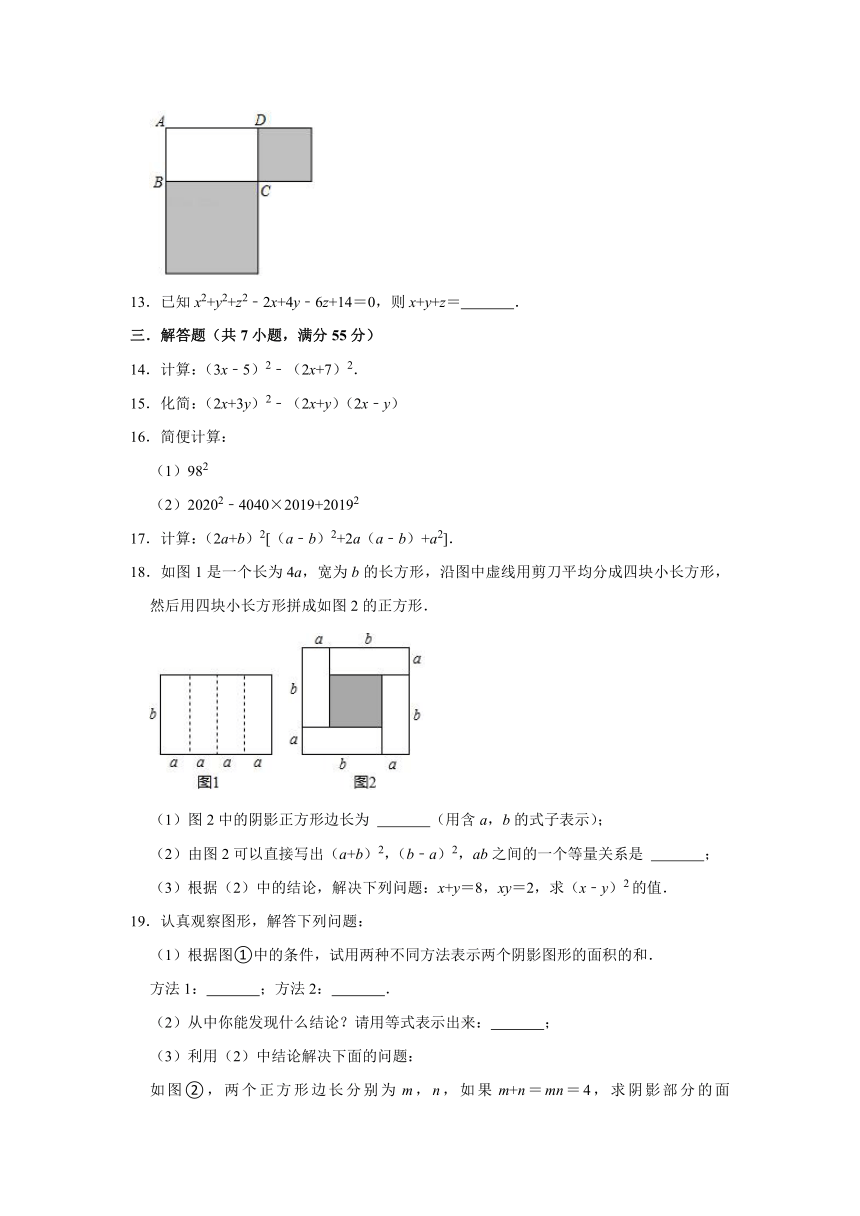
12.如图,长方形ABCD的周长为12,面积为3,分别以BC,CD为边作正方形,则图中阴影部分的面积为 .
13.已知x2+y2+z2﹣2x+4y﹣6z+14=0,则x+y+z= .
三.解答题(共7小题,满分55分)
14.计算:(3x﹣5)2﹣(2x+7)2.
15.化简:(2x+3y)2﹣(2x+y)(2x﹣y)
16.简便计算:
(1)982
(2)20202﹣4040×2019+20192
17.计算:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2].
18.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)图2中的阴影正方形边长为 (用含a,b的式子表示);
(2)由图2可以直接写出(a+b)2,(b﹣a)2,ab之间的一个等量关系是 ;
(3)根据(2)中的结论,解决下列问题:x+y=8,xy=2,求(x﹣y)2的值.
19.认真观察图形,解答下列问题:
(1)根据图①中的条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: ;方法2: .
(2)从中你能发现什么结论?请用等式表示出来: ;
(3)利用(2)中结论解决下面的问题:
如图②,两个正方形边长分别为m,n,如果m+n=mn=4,求阴影部分的面积.
20.阅读下列材料,解答下列问题:
例:若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值.
解:设80﹣x=a,x﹣60=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20.
∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340.
上述解题过程中,把某个式子看成一个整体,用一个变量来代替它,从而使问题得到简化,用到的是“整体思想”,整体思想是数学解题中常见的一种思想方法,请你运用这种方法解答下列问题:
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值.
(2)若x满足(2021﹣x)2+(2019﹣x)2=4048,求(2021﹣x)(2019﹣x)的值.
参考答案
一.选择题(共6小题,满分30分)
1.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
2.解:∵a﹣b=2,
∴(a﹣b)2=4,
∴a2﹣2ab+b2=4,
∴a2+b2=20,
∴20﹣2ab=4,
∴ab=8,
故选:C.
3.解:∵(x﹣1)2=2,
∴x2﹣2x+1=2,
∴x2﹣2x=1,
∴原式=1+5
=6,
故选:C.
4.解:x2+(a﹣1)x+25=x2+(a﹣1)x+52是完全平方式,则(a﹣1)x=±2 x 5,
解得:a=﹣9或11.
故选:B.
5.解:∵a+b=﹣2,ab=3,
∴a2﹣ab+b2
=(a+b)2﹣3ab
=(﹣2)2﹣3×3
=4﹣9
=﹣5.
故选:A.
6.解:∵(2022﹣x)(2020﹣x)=2021,
∴(2022﹣x)(x﹣2020)=﹣2021,
∵[(2022﹣x)+(x﹣2020)]2=(2022﹣x)2+(x﹣2020)2+2(2022﹣x)(x﹣2020),
∴原式=(2022﹣x)2+(x﹣2020)2
=[(2022﹣x)+(x﹣2020)]2﹣2(2022﹣x)(x﹣2020)
=4﹣2×(﹣2021)
=4+4042
=4046.
故选:C.
二.填空题(共7小题,满分35分)
7.解:∵(x+y)2=8,
∴x2+2xy+y2=8,
∵xy=3,
∴x2+6+y2=8,
∴x2+y2=2,
故答案为:2.
8.解:∵a+b=10,ab=﹣5,
∴a2+b2=(a+b)2﹣2ab=102﹣2×(﹣5)=100+10=110.
故答案为:110.
9.解:设x﹣2020=a,则x﹣2019=a+1,x﹣2021=a﹣1,
∵(x﹣2019)2+(x﹣2021)2=48,
∴(a+1)2+(a﹣1)2=48,
∴a2+2a+1+a2﹣2a+1=48,
∴2a2+2=48,
∴2a2=46,
∴a2=23,
即(x﹣2020)2=23.
故答案是:23.
10.解:因为x2﹣2(a﹣1)x+25=x2﹣2(a﹣1)x+52是完全平方式,
属于﹣2(a﹣1)x=±2 x 5,
解得:a=﹣4或6.
故答案为:﹣4或6.
11.解:由题意得,a2+b2﹣a2﹣(a+b)b=a2+b2﹣a2﹣ab﹣b2==,
∴当a+b=10,ab=8时,该阴影部分的面积为:===38,
故答案为:38.
12.解:设长方形ABCD的长为x,宽为y,
由题意得:,
∴x+y=6,
∴(x+y)2=36,
∴x2+2xy+y2=36,
∴x2+y2=36﹣2xy=36﹣6=30,
∴图中阴影部分的面积为30,
故答案为:30.
13.解:∵x2+y2+z2﹣2x+4y﹣6z+14=0,
∴x2﹣2x+1+y2+4y+4+z2﹣6z+9=0,
∴(x﹣1)2+(y+2)2+(z﹣3)2=0,
∴x﹣1=0,y+2=0,z﹣3=0,
∴x=1,y=﹣2,z=3,
故x+y+z=1﹣2+3=2.
故答案为:2.
三.解答题(共7小题,满分55分)
14.解:(3x﹣5)2﹣(2x+7)2
=(3x﹣5+2x+7)(3x﹣5﹣2x﹣7)
=(5x+2)(x﹣12)
=5x2﹣60x+2x﹣24
=5x2﹣58x﹣24.
15.解:原式=4x2+12xy+9y2﹣(4x2﹣y2)
=4x2+12xy+9y2﹣4x2+y2
=12xy+10y2.
16.解:(1))982=(100﹣2)2
=1002﹣2×100×2+22
=10000﹣400+4
=9604
(2)20202﹣4040×2019+20192
=20202﹣2×2020×2019+20192
=(2020﹣2019)2
=12
=1.
17.解:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2]
=(2a+b)2(a2﹣2ab+b2+2a2﹣2ab+a2)
=(2a+b)2(4a2﹣4ab+b2)
=(2a+b)2(2a﹣b)2
=(4a2﹣b2)2
=16a4﹣8a2b2+b4.
18.解:(1)由图2可得,阴影正方形边长为b﹣a,
故答案为:b﹣a;
(2)由图2面积的不同表示可得,
(a+b)2=(b﹣a)2+4ab,
故答案为:(a+b)2=(b﹣a)2+4ab;
(3)由(2)题中的结论(a+b)2=(b﹣a)2+4ab可得,
(b﹣a)2=(a+b)2﹣4ab,
∴当x+y=8,xy=2时,
(x﹣y)2=(x+y)2﹣4xy=82﹣4×2=64﹣8=56.
19.解:(1)阴影部分面积为两个正方形面积的和,即a2+b2;阴影部分面积为大正方形面积减去两个矩形面积,即(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)阴影部分面积相等,即得:a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)∵阴影部分的面积=S正方形ABCD+S正方形CGFE﹣S△ABD﹣S△BGF=m2+n2﹣m2﹣(m+n)n,
∴阴影部分的面积=m2+n2﹣mn=(m2+n2)﹣mn=[(m+n)2﹣2mn]﹣mn,
∵m+n=mn=4,
∴阴影部分的面积=[(m+n)2﹣2mn]﹣mn=×[42﹣2×4]﹣×4=2,
答:阴影部分面积为2.
20.解:(1)设30﹣x=m,x﹣20=n,
则(30﹣x)(x﹣20)=mn=﹣10,m+n=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=m2+n2=(m+n)2﹣2mn=100﹣2×(﹣10)=120;
(2)设2021﹣x=c,2019﹣x=d,
则(2021﹣x)﹣(2019﹣x)=c﹣d=2,
∵(2021﹣x)2+(2019﹣x)2=c2+d2=4048,
∴c2+d2=(c﹣d)2+2cd=4048,
∴4+2cd=4048,
∴2cd=4044,
∴cd=2022,
∴(2021﹣x)(2019﹣x)=2022.
一.选择题(共6小题,满分30分)
1.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
2.已知a﹣b=2,a2+b2=20,则ab值是( )
A.﹣8 B.12 C.8 D.9
3.已知(x﹣1)2=2,则代数式x2﹣2x+5的值为( )
A.4 B.5 C.6 D.7
4.若x2+(a﹣1)x+25是一个完全平方式,则a值为( )
A.﹣9 B.﹣9或11 C.9或﹣11 D.11
5.若a+b=﹣2,ab=3,则代数式a2﹣ab+b2的值是( )
A.﹣5 B.13 C.5 D.9
6.已知(2022﹣x)(2020﹣x)=2021,那么(2022﹣x)2+(2020﹣x)2的值是( )
A.20212 B.4042 C.4046 D.2021
二.填空题(共7小题,满分35分)
7.若(x+y)2=8,xy=3,则x2+y2= .
8.已知a+b=10,ab=﹣5,则a2+b2= .
9.已知(x﹣2019)2+(x﹣2021)2=48,则(x﹣2020)2= .
10.当a= 时,多项式x2﹣2(a﹣1)x+25是一个完全平方式.
11.如图,已知正方形ABCD与正方形CEFG的边长分别为a、b,如果a+b=10,ab=8,则阴影部分的面积为 .
12.如图,长方形ABCD的周长为12,面积为3,分别以BC,CD为边作正方形,则图中阴影部分的面积为 .
13.已知x2+y2+z2﹣2x+4y﹣6z+14=0,则x+y+z= .
三.解答题(共7小题,满分55分)
14.计算:(3x﹣5)2﹣(2x+7)2.
15.化简:(2x+3y)2﹣(2x+y)(2x﹣y)
16.简便计算:
(1)982
(2)20202﹣4040×2019+20192
17.计算:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2].
18.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)图2中的阴影正方形边长为 (用含a,b的式子表示);
(2)由图2可以直接写出(a+b)2,(b﹣a)2,ab之间的一个等量关系是 ;
(3)根据(2)中的结论,解决下列问题:x+y=8,xy=2,求(x﹣y)2的值.
19.认真观察图形,解答下列问题:
(1)根据图①中的条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: ;方法2: .
(2)从中你能发现什么结论?请用等式表示出来: ;
(3)利用(2)中结论解决下面的问题:
如图②,两个正方形边长分别为m,n,如果m+n=mn=4,求阴影部分的面积.
20.阅读下列材料,解答下列问题:
例:若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值.
解:设80﹣x=a,x﹣60=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20.
∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340.
上述解题过程中,把某个式子看成一个整体,用一个变量来代替它,从而使问题得到简化,用到的是“整体思想”,整体思想是数学解题中常见的一种思想方法,请你运用这种方法解答下列问题:
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值.
(2)若x满足(2021﹣x)2+(2019﹣x)2=4048,求(2021﹣x)(2019﹣x)的值.
参考答案
一.选择题(共6小题,满分30分)
1.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
2.解:∵a﹣b=2,
∴(a﹣b)2=4,
∴a2﹣2ab+b2=4,
∴a2+b2=20,
∴20﹣2ab=4,
∴ab=8,
故选:C.
3.解:∵(x﹣1)2=2,
∴x2﹣2x+1=2,
∴x2﹣2x=1,
∴原式=1+5
=6,
故选:C.
4.解:x2+(a﹣1)x+25=x2+(a﹣1)x+52是完全平方式,则(a﹣1)x=±2 x 5,
解得:a=﹣9或11.
故选:B.
5.解:∵a+b=﹣2,ab=3,
∴a2﹣ab+b2
=(a+b)2﹣3ab
=(﹣2)2﹣3×3
=4﹣9
=﹣5.
故选:A.
6.解:∵(2022﹣x)(2020﹣x)=2021,
∴(2022﹣x)(x﹣2020)=﹣2021,
∵[(2022﹣x)+(x﹣2020)]2=(2022﹣x)2+(x﹣2020)2+2(2022﹣x)(x﹣2020),
∴原式=(2022﹣x)2+(x﹣2020)2
=[(2022﹣x)+(x﹣2020)]2﹣2(2022﹣x)(x﹣2020)
=4﹣2×(﹣2021)
=4+4042
=4046.
故选:C.
二.填空题(共7小题,满分35分)
7.解:∵(x+y)2=8,
∴x2+2xy+y2=8,
∵xy=3,
∴x2+6+y2=8,
∴x2+y2=2,
故答案为:2.
8.解:∵a+b=10,ab=﹣5,
∴a2+b2=(a+b)2﹣2ab=102﹣2×(﹣5)=100+10=110.
故答案为:110.
9.解:设x﹣2020=a,则x﹣2019=a+1,x﹣2021=a﹣1,
∵(x﹣2019)2+(x﹣2021)2=48,
∴(a+1)2+(a﹣1)2=48,
∴a2+2a+1+a2﹣2a+1=48,
∴2a2+2=48,
∴2a2=46,
∴a2=23,
即(x﹣2020)2=23.
故答案是:23.
10.解:因为x2﹣2(a﹣1)x+25=x2﹣2(a﹣1)x+52是完全平方式,
属于﹣2(a﹣1)x=±2 x 5,
解得:a=﹣4或6.
故答案为:﹣4或6.
11.解:由题意得,a2+b2﹣a2﹣(a+b)b=a2+b2﹣a2﹣ab﹣b2==,
∴当a+b=10,ab=8时,该阴影部分的面积为:===38,
故答案为:38.
12.解:设长方形ABCD的长为x,宽为y,
由题意得:,
∴x+y=6,
∴(x+y)2=36,
∴x2+2xy+y2=36,
∴x2+y2=36﹣2xy=36﹣6=30,
∴图中阴影部分的面积为30,
故答案为:30.
13.解:∵x2+y2+z2﹣2x+4y﹣6z+14=0,
∴x2﹣2x+1+y2+4y+4+z2﹣6z+9=0,
∴(x﹣1)2+(y+2)2+(z﹣3)2=0,
∴x﹣1=0,y+2=0,z﹣3=0,
∴x=1,y=﹣2,z=3,
故x+y+z=1﹣2+3=2.
故答案为:2.
三.解答题(共7小题,满分55分)
14.解:(3x﹣5)2﹣(2x+7)2
=(3x﹣5+2x+7)(3x﹣5﹣2x﹣7)
=(5x+2)(x﹣12)
=5x2﹣60x+2x﹣24
=5x2﹣58x﹣24.
15.解:原式=4x2+12xy+9y2﹣(4x2﹣y2)
=4x2+12xy+9y2﹣4x2+y2
=12xy+10y2.
16.解:(1))982=(100﹣2)2
=1002﹣2×100×2+22
=10000﹣400+4
=9604
(2)20202﹣4040×2019+20192
=20202﹣2×2020×2019+20192
=(2020﹣2019)2
=12
=1.
17.解:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2]
=(2a+b)2(a2﹣2ab+b2+2a2﹣2ab+a2)
=(2a+b)2(4a2﹣4ab+b2)
=(2a+b)2(2a﹣b)2
=(4a2﹣b2)2
=16a4﹣8a2b2+b4.
18.解:(1)由图2可得,阴影正方形边长为b﹣a,
故答案为:b﹣a;
(2)由图2面积的不同表示可得,
(a+b)2=(b﹣a)2+4ab,
故答案为:(a+b)2=(b﹣a)2+4ab;
(3)由(2)题中的结论(a+b)2=(b﹣a)2+4ab可得,
(b﹣a)2=(a+b)2﹣4ab,
∴当x+y=8,xy=2时,
(x﹣y)2=(x+y)2﹣4xy=82﹣4×2=64﹣8=56.
19.解:(1)阴影部分面积为两个正方形面积的和,即a2+b2;阴影部分面积为大正方形面积减去两个矩形面积,即(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)阴影部分面积相等,即得:a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)∵阴影部分的面积=S正方形ABCD+S正方形CGFE﹣S△ABD﹣S△BGF=m2+n2﹣m2﹣(m+n)n,
∴阴影部分的面积=m2+n2﹣mn=(m2+n2)﹣mn=[(m+n)2﹣2mn]﹣mn,
∵m+n=mn=4,
∴阴影部分的面积=[(m+n)2﹣2mn]﹣mn=×[42﹣2×4]﹣×4=2,
答:阴影部分面积为2.
20.解:(1)设30﹣x=m,x﹣20=n,
则(30﹣x)(x﹣20)=mn=﹣10,m+n=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=m2+n2=(m+n)2﹣2mn=100﹣2×(﹣10)=120;
(2)设2021﹣x=c,2019﹣x=d,
则(2021﹣x)﹣(2019﹣x)=c﹣d=2,
∵(2021﹣x)2+(2019﹣x)2=c2+d2=4048,
∴c2+d2=(c﹣d)2+2cd=4048,
∴4+2cd=4048,
∴2cd=4044,
∴cd=2022,
∴(2021﹣x)(2019﹣x)=2022.
