2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)同步达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)同步达标测试(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 20:09:34 | ||
图片预览



文档简介
2021-2022学年苏科版七年级数学下册《第7章平面图形的认识(二)》
同步达标测试(附答案)
一.选择题(共8小题,满分40分)
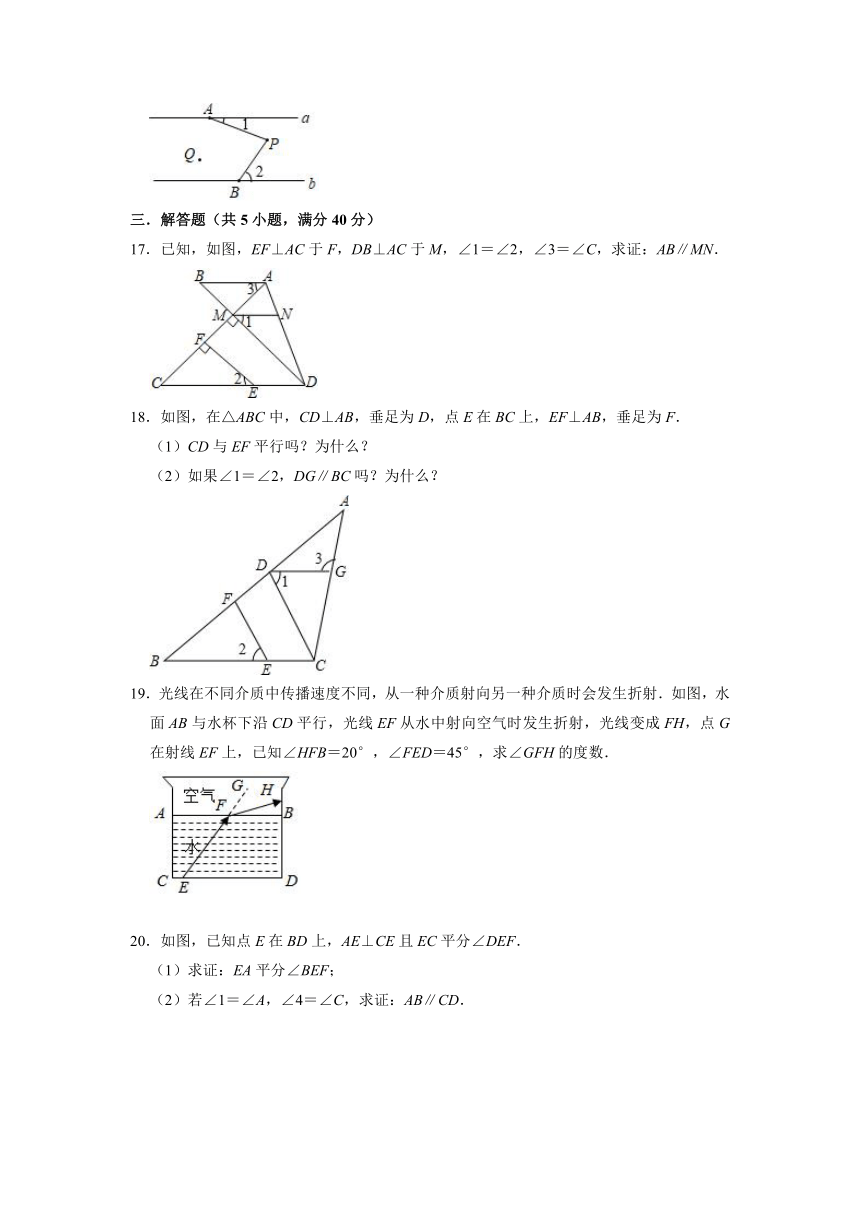
1.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2; ②∠1=∠3; ③∠2=∠4;
④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
2.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
3.如图,已知AD⊥BC,FG⊥BC,∠BAC=90°,DE∥AC.则结论:①FG∥AD;②DE平分∠ADB;③∠B=∠ADE;④∠CFG+∠BDE=90°.正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
4.如图,BD是四边形ABCD的对角线.若∠1=∠2,∠A=80°,则∠ADC等于( )
A.60° B.80° C.90° D.100°
5.如图所示,△ABC的边AC上的高是( )
A.线段AE B.线段BA C.线段BD D.线段DA
6.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4 B.5 C.12 D.13
7.如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A.14° B.24° C.19° D.9°
8.已知直线l1∥l2,将一块直角三角板ABC(其中∠A是30°,∠C是60°)按如图所示方式放置,若∠1=84°,则∠2等于( )
A.56° B.64° C.66° D.76°
二.填空题(共8小题,满分40分)
9.如图,共有 个三角形.
10.盖房子的时候,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条的根据是 .
11.如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为 .
12.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
13.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=83°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 度.
14.已知直线a∥b,用一块含30°角的直角三角板按图中所示的方式放置,若∠1=25°,则∠2= .
15.如图,将一张长方形纸片如图所示折叠后,如果∠1=130°,那么∠2等于 .
16.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折线段,且50°<∠APB<90°,Q是a,b之间且在折线段APB左侧的一点,如图.若∠AQC的一边与PA的夹角为40°,另一边与PB平行,请直接写出∠AQC,∠1,∠2之间满足的数量关系是 .
三.解答题(共5小题,满分40分)
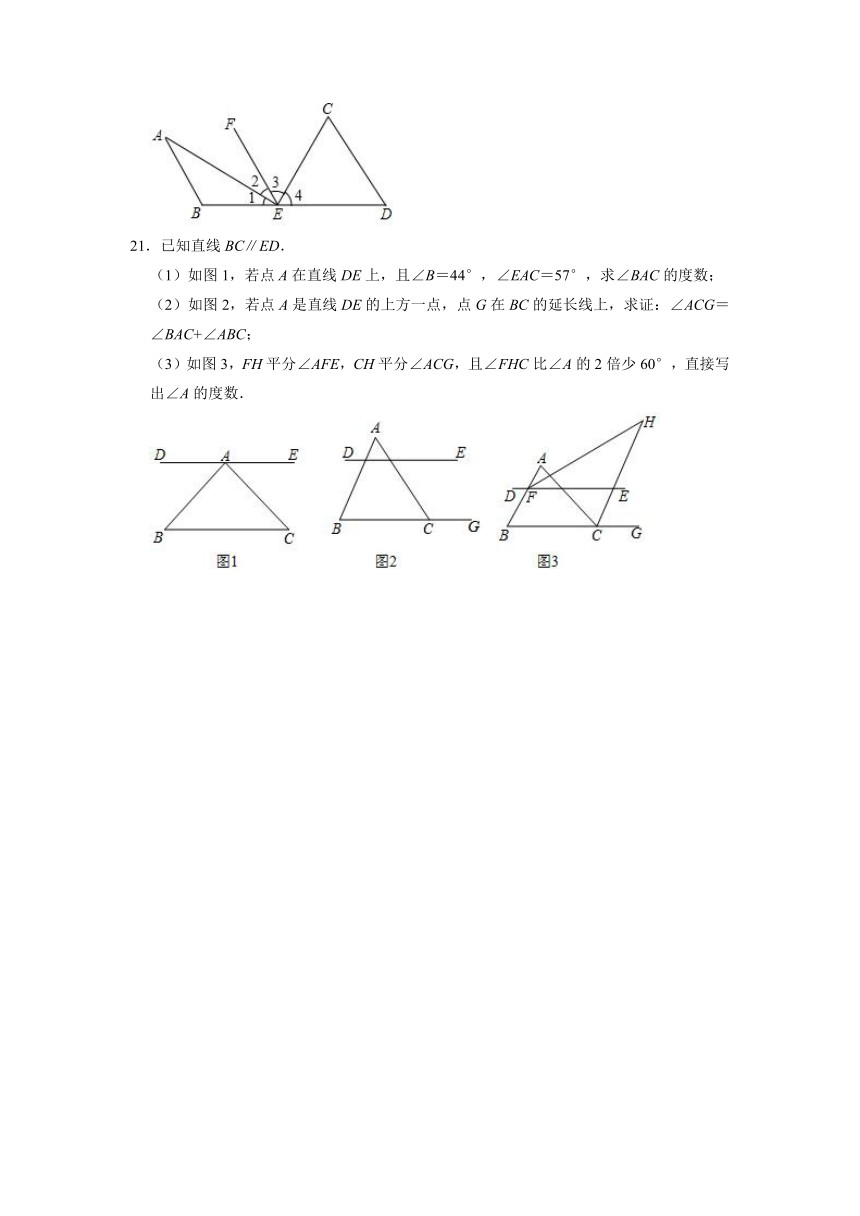
17.已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
18.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,DG∥BC吗?为什么?
19.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
20.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
21.已知直线BC∥ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上,求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.
参考答案
一.选择题(共8小题,满分40分)
1.解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
2.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
3.解:∵AD⊥BC,FG⊥BC,
∴∠FGD=∠ADB=90°,
∴FG∥AD,
故①正确;
∵DE∥AC,∠BAC=90°,
∴DE⊥AB,
不能证明DE为∠ADB的平分线,
故②错误;
∵AD⊥BC,
∴∠B+∠BAD=90°,
∵DE⊥AB,
∴∠BAD+∠ADE=90°,
∴∠B=∠ADE,
故③正确;
∵∠BAC=90°,DE⊥AB,
∴∠CFG+∠C=90°,∠BDE+∠B=90°,∠C+∠B=90°,
∴∠CFG+∠BDE=90°,
故④正确,
综上所述,正确的选项①③④,
故选:C.
4.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=80°,
∴∠ADC=180°﹣80°=100°,
故选:D.
5.解:由题意可知,△ABC的边AC上的高是线段BD.
故选:C.
6.解:设第三边的长为x,
∵三角形两边的长分别是4和8,
∴8﹣4<x<8+4,即4<x<12,
只有5有可能,
故选:B.
7.解:在△ABC中,∠B=45°,∠C=73°,
∴∠BAC=180°﹣∠B﹣∠C=62°.
∵AE平分∠BAC,
∴∠CAE=∠BAC=31°.
∵AD是BC边上的高,
∴AD⊥BC,
∴∠CAD=90°﹣∠C=17°,
∴∠DAE=∠CAE﹣∠CAD=31°﹣17°=14°.
故选:A.
8.解:∵∠3+∠4+∠A=180°,∠A=30°,∠4=∠1=84°,
∴∠3=180°﹣∠A﹣∠4=180°﹣30°﹣84°=66°.
又∵直线l1∥l2,
∴∠2=∠3=66°.
故选:C.
二.填空题(共8小题,满分40分)
9.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
10.解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性;
故答案为:三角形具有稳定性.
11.解:在△ABC中,∠B=36°,∠C=76°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣36°﹣76°=68°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=×68°=34°.
∵AE是△ABC的高,
∴∠AEC=90°.
在△ACE中,∠AEC=90°,∠C=76°,
∴∠CAE=180°﹣∠AEC﹣∠C=180°﹣90°﹣76°=14°.
∴∠DAE=∠CAD﹣∠CAE=34°﹣14°=20°.
故答案为:20°.
12.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
13.解:∵OD'∥AC,
∴∠BOD'=∠A=70°,
∴∠DOD'=83°﹣70°=13°.
故答案为:13.
14.解:过点B作EF∥a.
∵a∥b,
∴EF∥a∥b.
∴∠1=∠ABF,∠2=∠FBC.
∵△ABC是含30°角的直角三角形,
∴∠ABC=60°.
∵∠ABF+∠CBF=60°,
∴∠2=60°﹣25=35°.
故答案为:35°.
15.解:由折叠得,∠4=∠5,由平行线的性质得,∠5=∠3,
∴∠4=∠3=180°﹣∠1=50°,
∴∠2=180°﹣∠4﹣∠5=180°﹣50°﹣50°=80°,
故答案为:80°.
16.解:①作QC∥BP交AP于点C,PD∥a,连接AQ,
如图1所示:
∵PD∥a,b∥a,
∴PD∥b,
∴∠2=∠BPD,
又∵PD∥a,
∴∠1=∠APD,
又∵∠APB=∠APD+∠BPD,
∴∠APB=∠1+∠2,
又∵QC∥PD,
∴∠APB=∠ACQ,
∴∠ACQ=∠1+∠2,
又∵∠AQC+∠ACQ+∠QAC=180°,
∠QAC=40°,
∴∠AQC+∠ACQ=140°,
∴∠AQC+∠1+∠2=140°;
②作QC∥BP交AP于点D,直线b于点C,PH∥a,连接AQ,
如图2所示:
同理可得:∠ADQ=∠1+∠2,
∵∠AQC+∠AQD=180°,∠QAP+∠ADQ+∠AQD=180°,
∠AQC=∠QAP+∠ADQ,
∠QAP=40°,
∴∠AQC﹣∠1﹣∠2=40°.
如图3中,同法可得∠AQC=∠1+∠2+40°或∠AQC=220°﹣∠1﹣∠2.
综合所述:∠AQC,∠1,∠2之间满足的数量关系:
∠AQC+∠1+∠2=140°或∠AQC﹣∠1﹣∠2=40°或∠AQC=∠1+∠2+40°或∠AQC=220°﹣∠1﹣∠2.
三.解答题(共5小题,满分40分)
17.证明:∵EF⊥AC,DB⊥AC,
∴EF∥DM,
∴∠2=∠CDM,
∵∠1=∠2,
∴∠1=∠CDM,
∴MN∥CD,
∴∠C=∠AMN,
∵∠3=∠C,
∴∠3=∠AMN,
∴AB∥MN.
18.解:(1)CD∥EF,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF.
(2)DG∥BC,
理由是:∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
19.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB﹣∠HFB=45°﹣20°=25°.
20.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF;
(2)∵∠1=∠A,∠4=∠C,
∴∠1+∠A+∠4+∠C=2(∠1+∠4)=180°,
∴∠B+∠D=(180°﹣2∠1)+(180°﹣2∠4)=360°﹣2(∠1+∠4)=180°,
∴AB∥CD.
21.解:(1)∵BC∥ED,∠B=44°,
∴∠DAB=∠B=44°,
∵∠BAC=180°﹣∠DAB﹣∠EAC
∴∠BAC=180°﹣44°﹣57°=79°.
(2)过点A作MN∥BG,
∴∠ACG=∠MAC,∠ABC=∠MAB
而∠MAC=∠MAB+∠BAC
∴∠ACG=∠MAB+∠BAC=∠ABC+∠BAC.
(3)如图,设AC与FH交于点P
∵FH平分∠AFE,CH平分∠ACG
∴∠AFH=∠EFH=∠AFE,∠ACH=∠HCG=∠ACG
∵BC∥ED
∴∠AFE=∠B
∴∠AFH=∠B
∵∠A+∠B=∠ACG
∴∠ACH=∠ACG=∠A+∠B
在△APF和△CPH中
∵∠APF=∠CPH
∴∠A+∠B=∠A+∠B+∠FHC
∴∠FHC=∠A
∵∠FCH=2∠A﹣60°
∴∠A=2∠A﹣60°
∴∠A=40°.
同步达标测试(附答案)
一.选择题(共8小题,满分40分)
1.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2; ②∠1=∠3; ③∠2=∠4;
④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
2.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
3.如图,已知AD⊥BC,FG⊥BC,∠BAC=90°,DE∥AC.则结论:①FG∥AD;②DE平分∠ADB;③∠B=∠ADE;④∠CFG+∠BDE=90°.正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
4.如图,BD是四边形ABCD的对角线.若∠1=∠2,∠A=80°,则∠ADC等于( )
A.60° B.80° C.90° D.100°
5.如图所示,△ABC的边AC上的高是( )
A.线段AE B.线段BA C.线段BD D.线段DA
6.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4 B.5 C.12 D.13
7.如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A.14° B.24° C.19° D.9°
8.已知直线l1∥l2,将一块直角三角板ABC(其中∠A是30°,∠C是60°)按如图所示方式放置,若∠1=84°,则∠2等于( )
A.56° B.64° C.66° D.76°
二.填空题(共8小题,满分40分)
9.如图,共有 个三角形.
10.盖房子的时候,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条的根据是 .
11.如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为 .
12.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
13.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=83°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 度.
14.已知直线a∥b,用一块含30°角的直角三角板按图中所示的方式放置,若∠1=25°,则∠2= .
15.如图,将一张长方形纸片如图所示折叠后,如果∠1=130°,那么∠2等于 .
16.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折线段,且50°<∠APB<90°,Q是a,b之间且在折线段APB左侧的一点,如图.若∠AQC的一边与PA的夹角为40°,另一边与PB平行,请直接写出∠AQC,∠1,∠2之间满足的数量关系是 .
三.解答题(共5小题,满分40分)
17.已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
18.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,DG∥BC吗?为什么?
19.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
20.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
21.已知直线BC∥ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上,求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.
参考答案
一.选择题(共8小题,满分40分)
1.解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
2.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
3.解:∵AD⊥BC,FG⊥BC,
∴∠FGD=∠ADB=90°,
∴FG∥AD,
故①正确;
∵DE∥AC,∠BAC=90°,
∴DE⊥AB,
不能证明DE为∠ADB的平分线,
故②错误;
∵AD⊥BC,
∴∠B+∠BAD=90°,
∵DE⊥AB,
∴∠BAD+∠ADE=90°,
∴∠B=∠ADE,
故③正确;
∵∠BAC=90°,DE⊥AB,
∴∠CFG+∠C=90°,∠BDE+∠B=90°,∠C+∠B=90°,
∴∠CFG+∠BDE=90°,
故④正确,
综上所述,正确的选项①③④,
故选:C.
4.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=80°,
∴∠ADC=180°﹣80°=100°,
故选:D.
5.解:由题意可知,△ABC的边AC上的高是线段BD.
故选:C.
6.解:设第三边的长为x,
∵三角形两边的长分别是4和8,
∴8﹣4<x<8+4,即4<x<12,
只有5有可能,
故选:B.
7.解:在△ABC中,∠B=45°,∠C=73°,
∴∠BAC=180°﹣∠B﹣∠C=62°.
∵AE平分∠BAC,
∴∠CAE=∠BAC=31°.
∵AD是BC边上的高,
∴AD⊥BC,
∴∠CAD=90°﹣∠C=17°,
∴∠DAE=∠CAE﹣∠CAD=31°﹣17°=14°.
故选:A.
8.解:∵∠3+∠4+∠A=180°,∠A=30°,∠4=∠1=84°,
∴∠3=180°﹣∠A﹣∠4=180°﹣30°﹣84°=66°.
又∵直线l1∥l2,
∴∠2=∠3=66°.
故选:C.
二.填空题(共8小题,满分40分)
9.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
10.解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性;
故答案为:三角形具有稳定性.
11.解:在△ABC中,∠B=36°,∠C=76°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣36°﹣76°=68°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=×68°=34°.
∵AE是△ABC的高,
∴∠AEC=90°.
在△ACE中,∠AEC=90°,∠C=76°,
∴∠CAE=180°﹣∠AEC﹣∠C=180°﹣90°﹣76°=14°.
∴∠DAE=∠CAD﹣∠CAE=34°﹣14°=20°.
故答案为:20°.
12.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
13.解:∵OD'∥AC,
∴∠BOD'=∠A=70°,
∴∠DOD'=83°﹣70°=13°.
故答案为:13.
14.解:过点B作EF∥a.
∵a∥b,
∴EF∥a∥b.
∴∠1=∠ABF,∠2=∠FBC.
∵△ABC是含30°角的直角三角形,
∴∠ABC=60°.
∵∠ABF+∠CBF=60°,
∴∠2=60°﹣25=35°.
故答案为:35°.
15.解:由折叠得,∠4=∠5,由平行线的性质得,∠5=∠3,
∴∠4=∠3=180°﹣∠1=50°,
∴∠2=180°﹣∠4﹣∠5=180°﹣50°﹣50°=80°,
故答案为:80°.
16.解:①作QC∥BP交AP于点C,PD∥a,连接AQ,
如图1所示:
∵PD∥a,b∥a,
∴PD∥b,
∴∠2=∠BPD,
又∵PD∥a,
∴∠1=∠APD,
又∵∠APB=∠APD+∠BPD,
∴∠APB=∠1+∠2,
又∵QC∥PD,
∴∠APB=∠ACQ,
∴∠ACQ=∠1+∠2,
又∵∠AQC+∠ACQ+∠QAC=180°,
∠QAC=40°,
∴∠AQC+∠ACQ=140°,
∴∠AQC+∠1+∠2=140°;
②作QC∥BP交AP于点D,直线b于点C,PH∥a,连接AQ,
如图2所示:
同理可得:∠ADQ=∠1+∠2,
∵∠AQC+∠AQD=180°,∠QAP+∠ADQ+∠AQD=180°,
∠AQC=∠QAP+∠ADQ,
∠QAP=40°,
∴∠AQC﹣∠1﹣∠2=40°.
如图3中,同法可得∠AQC=∠1+∠2+40°或∠AQC=220°﹣∠1﹣∠2.
综合所述:∠AQC,∠1,∠2之间满足的数量关系:
∠AQC+∠1+∠2=140°或∠AQC﹣∠1﹣∠2=40°或∠AQC=∠1+∠2+40°或∠AQC=220°﹣∠1﹣∠2.
三.解答题(共5小题,满分40分)
17.证明:∵EF⊥AC,DB⊥AC,
∴EF∥DM,
∴∠2=∠CDM,
∵∠1=∠2,
∴∠1=∠CDM,
∴MN∥CD,
∴∠C=∠AMN,
∵∠3=∠C,
∴∠3=∠AMN,
∴AB∥MN.
18.解:(1)CD∥EF,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF.
(2)DG∥BC,
理由是:∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
19.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB﹣∠HFB=45°﹣20°=25°.
20.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF;
(2)∵∠1=∠A,∠4=∠C,
∴∠1+∠A+∠4+∠C=2(∠1+∠4)=180°,
∴∠B+∠D=(180°﹣2∠1)+(180°﹣2∠4)=360°﹣2(∠1+∠4)=180°,
∴AB∥CD.
21.解:(1)∵BC∥ED,∠B=44°,
∴∠DAB=∠B=44°,
∵∠BAC=180°﹣∠DAB﹣∠EAC
∴∠BAC=180°﹣44°﹣57°=79°.
(2)过点A作MN∥BG,
∴∠ACG=∠MAC,∠ABC=∠MAB
而∠MAC=∠MAB+∠BAC
∴∠ACG=∠MAB+∠BAC=∠ABC+∠BAC.
(3)如图,设AC与FH交于点P
∵FH平分∠AFE,CH平分∠ACG
∴∠AFH=∠EFH=∠AFE,∠ACH=∠HCG=∠ACG
∵BC∥ED
∴∠AFE=∠B
∴∠AFH=∠B
∵∠A+∠B=∠ACG
∴∠ACH=∠ACG=∠A+∠B
在△APF和△CPH中
∵∠APF=∠CPH
∴∠A+∠B=∠A+∠B+∠FHC
∴∠FHC=∠A
∵∠FCH=2∠A﹣60°
∴∠A=2∠A﹣60°
∴∠A=40°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
