2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质与判定同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质与判定同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 20:15:35 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》同步练习题(附答案)
1.下列关于四边形的说法,正确的是( )
A.四个角相等的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.有两边相等的平行四边形是菱形
D.两条对角线相等的平行四边形是矩形
2.已知 ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
3.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,AC=3、AB=4、BC=5,P为BC上一动点,PG⊥AC于点G,PH⊥AB于点H,M是GH的中点,P在运动过程中PM的最小值为( )
A.2.4 B.1.4 C.1.3 D.1.2
5.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
6.矩形ABCD的对角线AC和BD相交于点O,∠ACB=40°,则∠AOB= °.
7.如图,在矩形ABCD中,AD=13,AB=5,E为BC上一点,DE平分∠AEC,则CE的长为 .
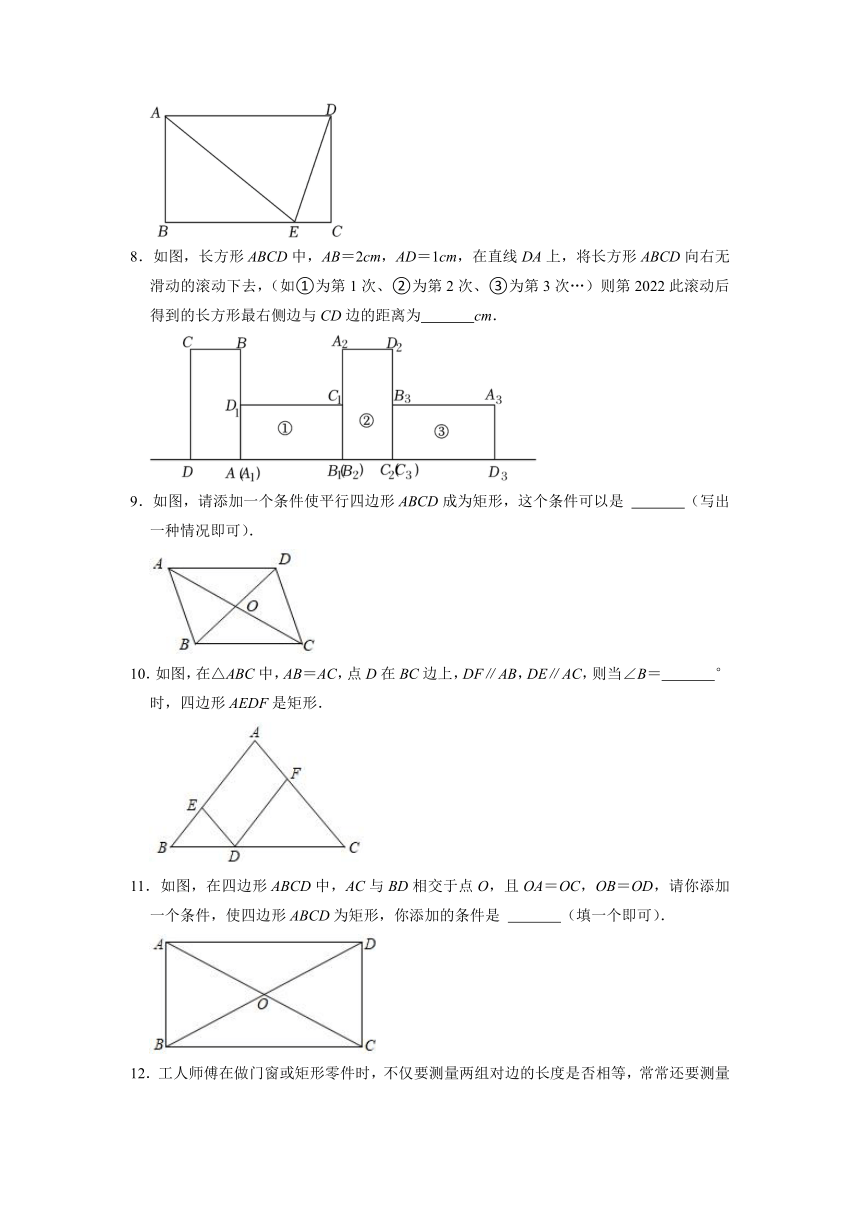
8.如图,长方形ABCD中,AB=2cm,AD=1cm,在直线DA上,将长方形ABCD向右无滑动的滚动下去,(如①为第1次、②为第2次、③为第3次…)则第2022此滚动后得到的长方形最右侧边与CD边的距离为 cm.
9.如图,请添加一个条件使平行四边形ABCD成为矩形,这个条件可以是 (写出一种情况即可).
10.如图,在△ABC中,AB=AC,点D在BC边上,DF∥AB,DE∥AC,则当∠B= °时,四边形AEDF是矩形.
11.如图,在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD,请你添加一个条件,使四边形ABCD为矩形,你添加的条件是 (填一个即可).
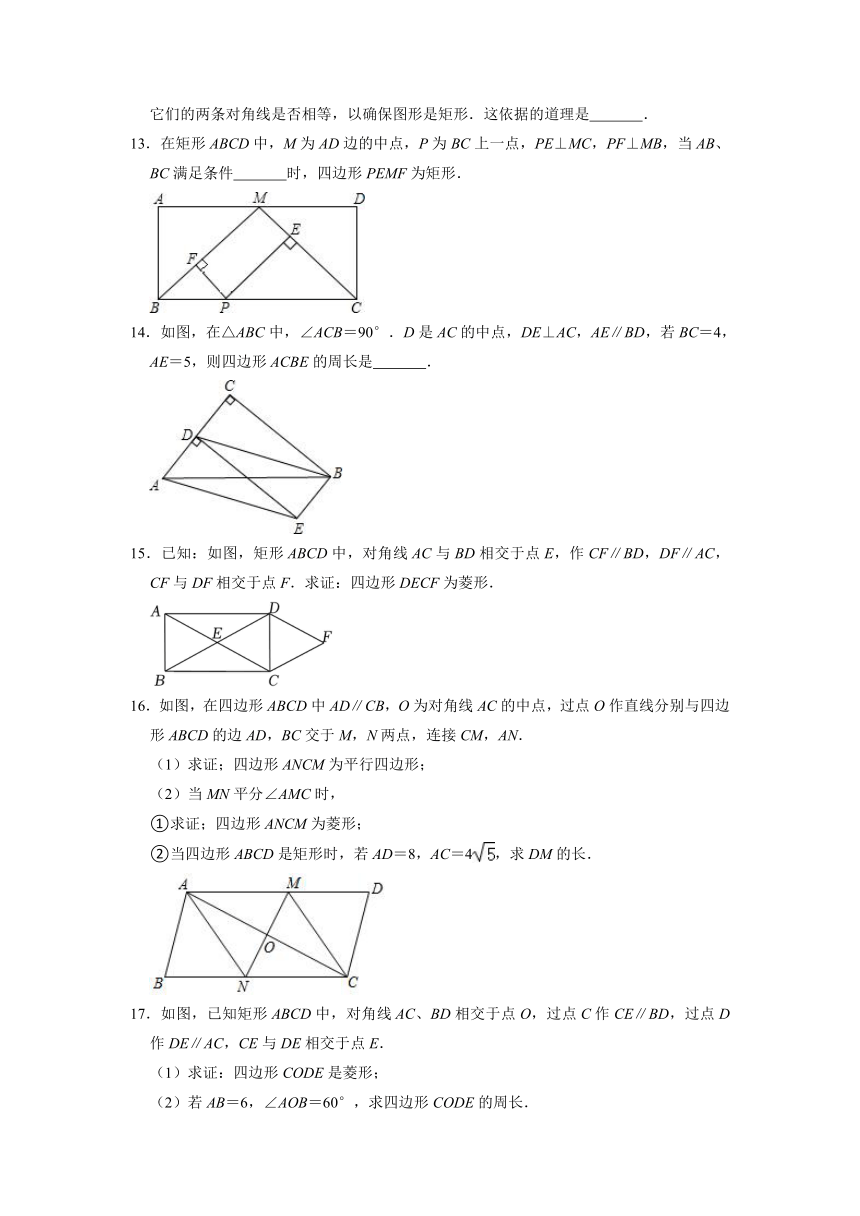
12.工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.这依据的道理是 .
13.在矩形ABCD中,M为AD边的中点,P为BC上一点,PE⊥MC,PF⊥MB,当AB、BC满足条件 时,四边形PEMF为矩形.
14.如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是 .
15.已知:如图,矩形ABCD中,对角线AC与BD相交于点E,作CF∥BD,DF∥AC,CF与DF相交于点F.求证:四边形DECF为菱形.
16.如图,在四边形ABCD中AD∥CB,O为对角线AC的中点,过点O作直线分别与四边形ABCD的边AD,BC交于M,N两点,连接CM,AN.
(1)求证;四边形ANCM为平行四边形;
(2)当MN平分∠AMC时,
①求证;四边形ANCM为菱形;
②当四边形ABCD是矩形时,若AD=8,AC=4,求DM的长.
17.如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是菱形;
(2)若AB=6,∠AOB=60°,求四边形CODE的周长.
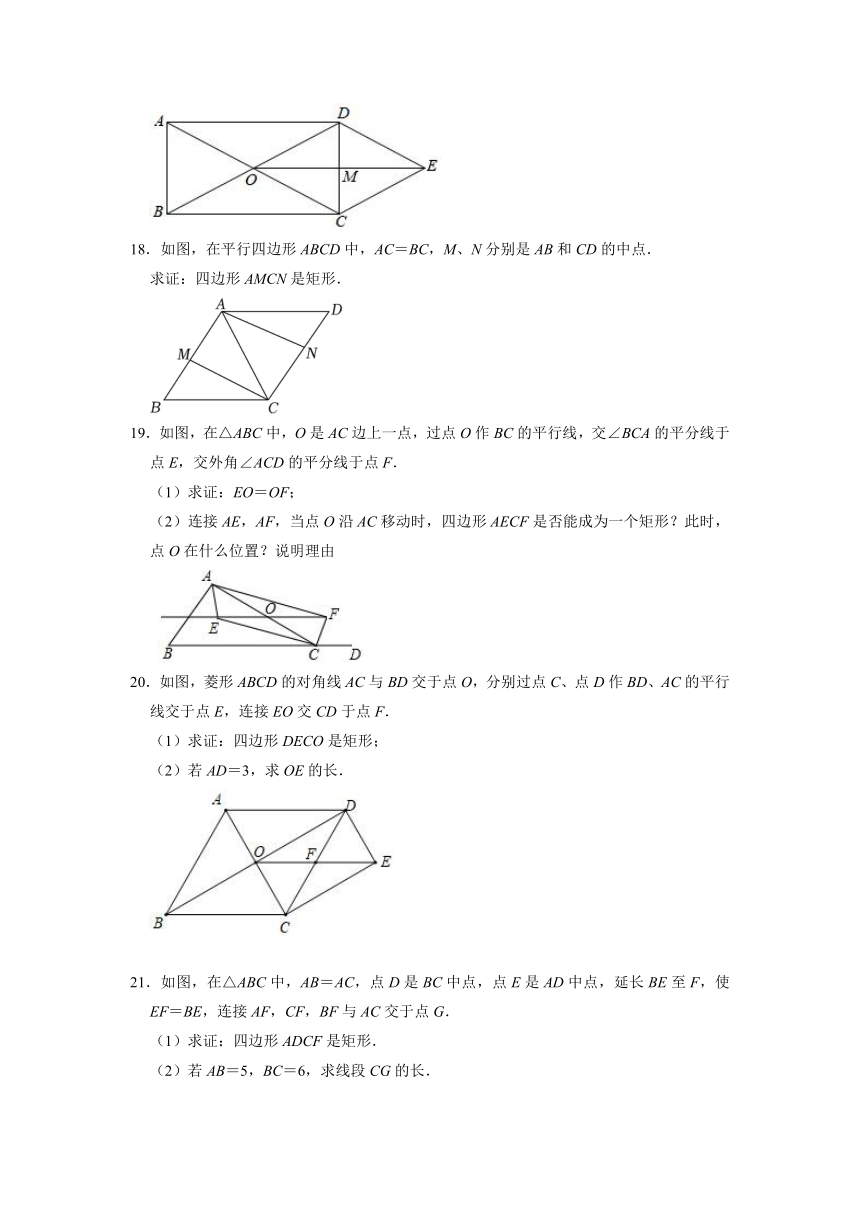
18.如图,在平行四边形ABCD中,AC=BC,M、N分别是AB和CD的中点.
求证:四边形AMCN是矩形.
19.如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E,交外角∠ACD的平分线于点F.
(1)求证:EO=OF;
(2)连接AE,AF,当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由
20.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
21.如图,在△ABC中,AB=AC,点D是BC中点,点E是AD中点,延长BE至F,使EF=BE,连接AF,CF,BF与AC交于点G.
(1)求证:四边形ADCF是矩形.
(2)若AB=5,BC=6,求线段CG的长.
参考答案
1.解:A、四个角相等的四边形是矩形,说法错误,不符合题意;
B、对角线互相平分且相等的四边形是矩形,说法错误,不符合题意;
C、有两邻边相等的平行四边形是菱形,说法错误,不符合题意;
D、两条对角线相等的平行四边形是矩形,说法正确,符合题意;
故选:D.
2.解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD为矩形,故选项A不符合题意;
B、∠A=∠C不能判定 ABCD为矩形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD是矩形,故选项C不符合题意;
D、∵AB⊥BC,
∴∠B=90°,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
3.解:①∵∠1+∠3=90°,
∴∠ABC=90°,
∴ ABCD是矩形,故①正确;
②∵四边形ABCD是平行四边形,
∴AB=CD,
∵BC2+CD2=AC2,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∴ ABCD是矩形,故②正确;
③∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵∠1=∠2,
∴OA=OB,
∴AC=BD,
∴ ABCD是矩形,故③正确;
④∵四边形ABCD是平行四边形,AC⊥BD,
∴ ABCD是菱形,故④错误;
能判定四边形ABCD是矩形的个数有3个,
故选:C.
4.解:连接PA,如图所示:
∵AC=3、AB=4、BC=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∵PG⊥AC于点G,PH⊥AB于点H,
∴∠PGA=∠PHA=90°,
∴四边形AGPH为矩形,
∴AP与GH互相平分且相等,
∵M是GH的中点,
∴M是AP的中点,
当AP⊥BC时,AP最小,
此时,△ABC的面积BC×AP=AC×AB,
则AP===2.4,
∴PM=AP=1.2,
即PM的最小值为1.2,
故选:D.
5.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
6.解:∵矩形ABCD的对角线AC,BD相交于点O,
∴OB=OC,
∴∠OBC=∠ACB=40°,
∴∠AOB=∠OBC+∠ACB=40°+40°=80°.
故答案为:80.
7.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
∵DE平分∠AEC,
∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=13,
在直角△ABE中,BE===12,
∴CE=BC﹣BE=AD﹣BE=13﹣12=1.
故答案为1.
8.解:∵四边形ABCD是矩形,
∴AB=CD=2(cm),BC=AD=1(cm),
第1次滚动后得到的长方形最右侧边与CD边的距离=1+2=3(cm),
第2次滚动后得到的长方形最右侧边与CD边的距离=1+2+1=4(cm),
第3次滚动后得到的长方形最右侧边与CD边的距离=1+2+1+2=6(cm),
第4次滚动后得到的长方形最右侧边与CD边的距离=1+2+1+2+1=7(cm),
第2022次滚动后得到的长方形最右侧边与CD边的距离=1+3×=3034(cm),
故答案为:3034.
9.解:若使平行四边形ABCD变为矩形,可添加的条件是:
AC=BD;(对角线相等的平行四边形是矩形)
∠ABC=90°.(有一个角是直角的平行四边形是矩形)
故答案为:AC=BD或∠ABC=90°.
10.解:当∠B=45°时,四边形AEDF是矩形.
∵DF∥AB,DE∥AC,
∴四边形AEDF是平行四边形,
∵AB=AC,
∴∠B=∠C=45°,
∴∠A=90°,
∴四边形AEDF是矩形.
故答案为45.
11.解:添加条件:OA=OB,理由如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵OA=OB,
∴OA=OC=OB=OD,
∴OA+OC=OB+OD,
即AC=BD,
∴平行四边形ABCD是矩形,
故答案为:OA=OB(答案不唯一).
12.解:因为门窗所构成的形状是矩形,
所以根据矩形的判定(对角线相等的平行四边形为矩形)可得出.
故答案为:对角线相等的平行四边形是矩形.
13.解:AB=BC时,四边形PEMF是矩形.
∵在矩形ABCD中,M为AD边的中点,AB=BC,
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
14.解:∵AE∥BD,
∴∠CDB=∠DAE,
∵∠ACB=90°,DE⊥AC,
∴∠C=∠ADE=90°,
∴DE∥BC,
∵D为AC中点,
∴AD=CD,
在△ADE和△DCB中
∵,
∴△ADE≌△DCB(ASA),
∴DE=BC=4,
在Rt△DCB中,BC=4,BD=5,由勾股定理得:DC=3,
∴AD=DC=3,
∵ED=BC,DE∥BC,
∴四边形DEBC是平行四边形,
∴CD=BE=3,
∴四边形ACBE的周长是AC+BC+BE+AE=3+3+4+3+5=18,
故答案为:18.
15.证明:∵CF∥BD,DF∥AC,
∴四边形DECF是平行四边形,
∵四边形ABCD是矩形,
∴CE=AC,DE=BD,AC=BD,
∴CE=DE,
∴平行四边形DECF为菱形.
16.(1)证明:∵AD∥BC,O为对角线AC的中点,
∴AO=CO,∠OAM=∠OCN,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴AM=CN,
∵AM∥CN,
∴四边形ANCM为平行四边形;
(2)解:①∵MN平分∠AMC,
∴∠AMN=∠CMN,
∵AD∥BC,
∴∠AMN=∠CNM,
∴∠CMN=∠CNM,
∴CM=CN,
∴平行四边形ANCM为菱形;
②∵四边形ABCD是矩形,
∴∠ABN=90°,BC=AD=8,
∴AB===4,AM=AN=NC=AD﹣DM,
在Rt△ABN中,根据勾股定理,得
AN2=AB2+BN2,
∴(8﹣DM)2=42+DM2,
解得DM=3.
故DM的长为3.
17.(1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∴OD=OC=OA=OB,
∴四边形CODE是菱形;
(2)解:∵∠AOB=60°,AO=BO,
∴△AOB是等边三角形,
∴OA=OB=AB=6=OC,
∵四边形CODE是菱形,
∴OC=OD=DE=CE=6,
∴四边形CODE的周长=6×4=24.
18.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AM∥CN,
∵M、N分别是AB和CD的中点,
∴AM=AB,CN=CD,
∴AM=CN,
∴四边形AMCN是平行四边形,
∵AC=BC,
∴△ACB是等腰三角形,
∵M是AB的中点,
∴CM是△ACB的边AB上的高,
∴∠AMC=90°,
∴平行四边形AMCN是矩形.
19.(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形;理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,
即AC=EF,
∴平行四边形AECF是矩形,
即当点O沿AC移动时,四边形AECF能成为一个矩形,此时,点O在AC的中点.
20.(1)证明:∵CE∥BD,DE∥AC,
∴四边形DECO是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形DECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AD=3,
由(1)得:四边形DECO是矩形,
∴OE=CD=3.
21.(1)证明:∵点E是AD中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(SAS),
∴AF=DB,∠AFE=∠DBE,
∴AF∥DB,
∵AB=AC,点D是BC中点,
∴DB=DC,AD⊥BC,
∴AF=DC,∠ADC=90°,
∴四边形ADCF是平行四边形,
∵∠ADC=90°,
∴平行四边形ADCF是矩形;
(2)解:过G作GH⊥CD于H,如图所示:
则GH∥AD,
∵AB=AC=5,点D是BC中点,
∴AD⊥BC,BD=CD=BC=3,
∴AD===4,
由(1)得:AF=DC=BD=3=BC,AF∥BC,
∴AG=CG,
∴AG=AC=,
∴CG=AC﹣AG=5﹣=,
故答案为:.
1.下列关于四边形的说法,正确的是( )
A.四个角相等的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.有两边相等的平行四边形是菱形
D.两条对角线相等的平行四边形是矩形
2.已知 ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
3.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,AC=3、AB=4、BC=5,P为BC上一动点,PG⊥AC于点G,PH⊥AB于点H,M是GH的中点,P在运动过程中PM的最小值为( )
A.2.4 B.1.4 C.1.3 D.1.2
5.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
6.矩形ABCD的对角线AC和BD相交于点O,∠ACB=40°,则∠AOB= °.
7.如图,在矩形ABCD中,AD=13,AB=5,E为BC上一点,DE平分∠AEC,则CE的长为 .
8.如图,长方形ABCD中,AB=2cm,AD=1cm,在直线DA上,将长方形ABCD向右无滑动的滚动下去,(如①为第1次、②为第2次、③为第3次…)则第2022此滚动后得到的长方形最右侧边与CD边的距离为 cm.
9.如图,请添加一个条件使平行四边形ABCD成为矩形,这个条件可以是 (写出一种情况即可).
10.如图,在△ABC中,AB=AC,点D在BC边上,DF∥AB,DE∥AC,则当∠B= °时,四边形AEDF是矩形.
11.如图,在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD,请你添加一个条件,使四边形ABCD为矩形,你添加的条件是 (填一个即可).
12.工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.这依据的道理是 .
13.在矩形ABCD中,M为AD边的中点,P为BC上一点,PE⊥MC,PF⊥MB,当AB、BC满足条件 时,四边形PEMF为矩形.
14.如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是 .
15.已知:如图,矩形ABCD中,对角线AC与BD相交于点E,作CF∥BD,DF∥AC,CF与DF相交于点F.求证:四边形DECF为菱形.
16.如图,在四边形ABCD中AD∥CB,O为对角线AC的中点,过点O作直线分别与四边形ABCD的边AD,BC交于M,N两点,连接CM,AN.
(1)求证;四边形ANCM为平行四边形;
(2)当MN平分∠AMC时,
①求证;四边形ANCM为菱形;
②当四边形ABCD是矩形时,若AD=8,AC=4,求DM的长.
17.如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是菱形;
(2)若AB=6,∠AOB=60°,求四边形CODE的周长.
18.如图,在平行四边形ABCD中,AC=BC,M、N分别是AB和CD的中点.
求证:四边形AMCN是矩形.
19.如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E,交外角∠ACD的平分线于点F.
(1)求证:EO=OF;
(2)连接AE,AF,当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由
20.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
21.如图,在△ABC中,AB=AC,点D是BC中点,点E是AD中点,延长BE至F,使EF=BE,连接AF,CF,BF与AC交于点G.
(1)求证:四边形ADCF是矩形.
(2)若AB=5,BC=6,求线段CG的长.
参考答案
1.解:A、四个角相等的四边形是矩形,说法错误,不符合题意;
B、对角线互相平分且相等的四边形是矩形,说法错误,不符合题意;
C、有两邻边相等的平行四边形是菱形,说法错误,不符合题意;
D、两条对角线相等的平行四边形是矩形,说法正确,符合题意;
故选:D.
2.解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD为矩形,故选项A不符合题意;
B、∠A=∠C不能判定 ABCD为矩形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD是矩形,故选项C不符合题意;
D、∵AB⊥BC,
∴∠B=90°,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
3.解:①∵∠1+∠3=90°,
∴∠ABC=90°,
∴ ABCD是矩形,故①正确;
②∵四边形ABCD是平行四边形,
∴AB=CD,
∵BC2+CD2=AC2,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∴ ABCD是矩形,故②正确;
③∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵∠1=∠2,
∴OA=OB,
∴AC=BD,
∴ ABCD是矩形,故③正确;
④∵四边形ABCD是平行四边形,AC⊥BD,
∴ ABCD是菱形,故④错误;
能判定四边形ABCD是矩形的个数有3个,
故选:C.
4.解:连接PA,如图所示:
∵AC=3、AB=4、BC=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∵PG⊥AC于点G,PH⊥AB于点H,
∴∠PGA=∠PHA=90°,
∴四边形AGPH为矩形,
∴AP与GH互相平分且相等,
∵M是GH的中点,
∴M是AP的中点,
当AP⊥BC时,AP最小,
此时,△ABC的面积BC×AP=AC×AB,
则AP===2.4,
∴PM=AP=1.2,
即PM的最小值为1.2,
故选:D.
5.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
6.解:∵矩形ABCD的对角线AC,BD相交于点O,
∴OB=OC,
∴∠OBC=∠ACB=40°,
∴∠AOB=∠OBC+∠ACB=40°+40°=80°.
故答案为:80.
7.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
∵DE平分∠AEC,
∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=13,
在直角△ABE中,BE===12,
∴CE=BC﹣BE=AD﹣BE=13﹣12=1.
故答案为1.
8.解:∵四边形ABCD是矩形,
∴AB=CD=2(cm),BC=AD=1(cm),
第1次滚动后得到的长方形最右侧边与CD边的距离=1+2=3(cm),
第2次滚动后得到的长方形最右侧边与CD边的距离=1+2+1=4(cm),
第3次滚动后得到的长方形最右侧边与CD边的距离=1+2+1+2=6(cm),
第4次滚动后得到的长方形最右侧边与CD边的距离=1+2+1+2+1=7(cm),
第2022次滚动后得到的长方形最右侧边与CD边的距离=1+3×=3034(cm),
故答案为:3034.
9.解:若使平行四边形ABCD变为矩形,可添加的条件是:
AC=BD;(对角线相等的平行四边形是矩形)
∠ABC=90°.(有一个角是直角的平行四边形是矩形)
故答案为:AC=BD或∠ABC=90°.
10.解:当∠B=45°时,四边形AEDF是矩形.
∵DF∥AB,DE∥AC,
∴四边形AEDF是平行四边形,
∵AB=AC,
∴∠B=∠C=45°,
∴∠A=90°,
∴四边形AEDF是矩形.
故答案为45.
11.解:添加条件:OA=OB,理由如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵OA=OB,
∴OA=OC=OB=OD,
∴OA+OC=OB+OD,
即AC=BD,
∴平行四边形ABCD是矩形,
故答案为:OA=OB(答案不唯一).
12.解:因为门窗所构成的形状是矩形,
所以根据矩形的判定(对角线相等的平行四边形为矩形)可得出.
故答案为:对角线相等的平行四边形是矩形.
13.解:AB=BC时,四边形PEMF是矩形.
∵在矩形ABCD中,M为AD边的中点,AB=BC,
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
14.解:∵AE∥BD,
∴∠CDB=∠DAE,
∵∠ACB=90°,DE⊥AC,
∴∠C=∠ADE=90°,
∴DE∥BC,
∵D为AC中点,
∴AD=CD,
在△ADE和△DCB中
∵,
∴△ADE≌△DCB(ASA),
∴DE=BC=4,
在Rt△DCB中,BC=4,BD=5,由勾股定理得:DC=3,
∴AD=DC=3,
∵ED=BC,DE∥BC,
∴四边形DEBC是平行四边形,
∴CD=BE=3,
∴四边形ACBE的周长是AC+BC+BE+AE=3+3+4+3+5=18,
故答案为:18.
15.证明:∵CF∥BD,DF∥AC,
∴四边形DECF是平行四边形,
∵四边形ABCD是矩形,
∴CE=AC,DE=BD,AC=BD,
∴CE=DE,
∴平行四边形DECF为菱形.
16.(1)证明:∵AD∥BC,O为对角线AC的中点,
∴AO=CO,∠OAM=∠OCN,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴AM=CN,
∵AM∥CN,
∴四边形ANCM为平行四边形;
(2)解:①∵MN平分∠AMC,
∴∠AMN=∠CMN,
∵AD∥BC,
∴∠AMN=∠CNM,
∴∠CMN=∠CNM,
∴CM=CN,
∴平行四边形ANCM为菱形;
②∵四边形ABCD是矩形,
∴∠ABN=90°,BC=AD=8,
∴AB===4,AM=AN=NC=AD﹣DM,
在Rt△ABN中,根据勾股定理,得
AN2=AB2+BN2,
∴(8﹣DM)2=42+DM2,
解得DM=3.
故DM的长为3.
17.(1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∴OD=OC=OA=OB,
∴四边形CODE是菱形;
(2)解:∵∠AOB=60°,AO=BO,
∴△AOB是等边三角形,
∴OA=OB=AB=6=OC,
∵四边形CODE是菱形,
∴OC=OD=DE=CE=6,
∴四边形CODE的周长=6×4=24.
18.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AM∥CN,
∵M、N分别是AB和CD的中点,
∴AM=AB,CN=CD,
∴AM=CN,
∴四边形AMCN是平行四边形,
∵AC=BC,
∴△ACB是等腰三角形,
∵M是AB的中点,
∴CM是△ACB的边AB上的高,
∴∠AMC=90°,
∴平行四边形AMCN是矩形.
19.(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形;理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,
即AC=EF,
∴平行四边形AECF是矩形,
即当点O沿AC移动时,四边形AECF能成为一个矩形,此时,点O在AC的中点.
20.(1)证明:∵CE∥BD,DE∥AC,
∴四边形DECO是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形DECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AD=3,
由(1)得:四边形DECO是矩形,
∴OE=CD=3.
21.(1)证明:∵点E是AD中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(SAS),
∴AF=DB,∠AFE=∠DBE,
∴AF∥DB,
∵AB=AC,点D是BC中点,
∴DB=DC,AD⊥BC,
∴AF=DC,∠ADC=90°,
∴四边形ADCF是平行四边形,
∵∠ADC=90°,
∴平行四边形ADCF是矩形;
(2)解:过G作GH⊥CD于H,如图所示:
则GH∥AD,
∵AB=AC=5,点D是BC中点,
∴AD⊥BC,BD=CD=BC=3,
∴AD===4,
由(1)得:AF=DC=BD=3=BC,AF∥BC,
∴AG=CG,
∴AG=AC=,
∴CG=AC﹣AG=5﹣=,
故答案为:.
