2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定同步练习题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步达标测试(附答案)
一.选择题(共6小题,满分24分)
1.如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当AC=BD时,它是矩形
D.当∠ABC=90°时,它是正方形
2.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=( )
A. B. C.6 D.
3.如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
4.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣2,0),B(2,b),则正方形ABCD的面积是( )
A.34 B.25 C.20 D.16
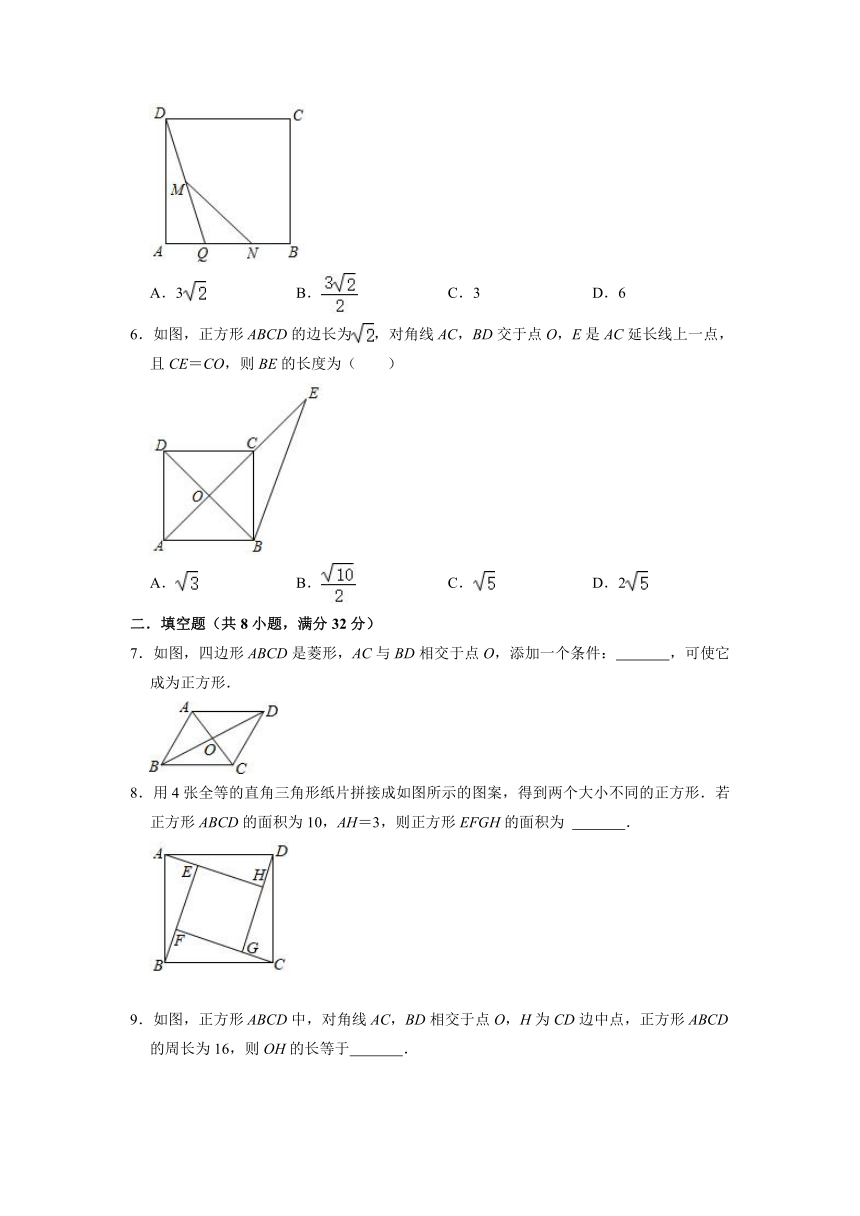
5.如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=( )
A.3 B. C.3 D.6
6.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为( )
A. B. C. D.2
二.填空题(共8小题,满分32分)
7.如图,四边形ABCD是菱形,AC与BD相交于点O,添加一个条件: ,可使它成为正方形.
8.用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形.若正方形ABCD的面积为10,AH=3,则正方形EFGH的面积为 .
9.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为16,则OH的长等于 .
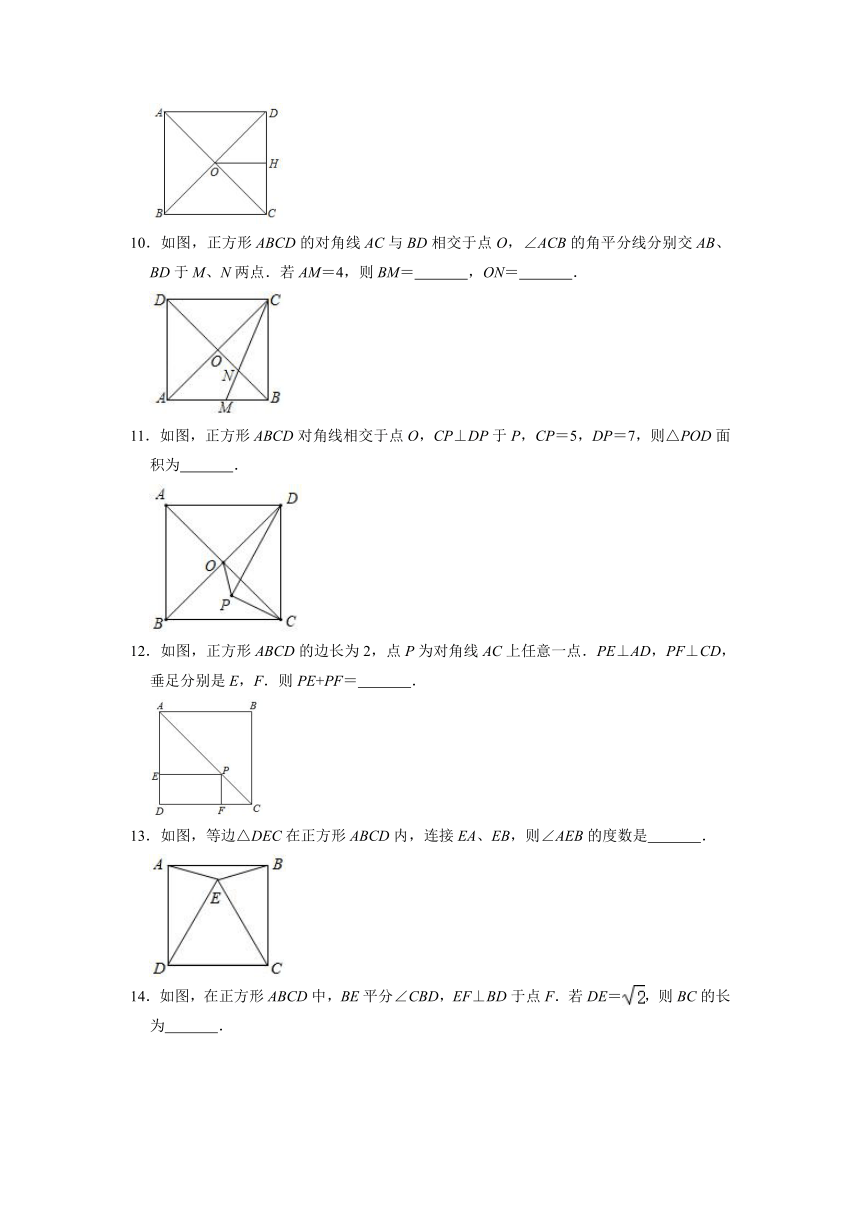
10.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点.若AM=4,则BM= ,ON= .
11.如图,正方形ABCD对角线相交于点O,CP⊥DP于P,CP=5,DP=7,则△POD面积为 .
12.如图,正方形ABCD的边长为2,点P为对角线AC上任意一点.PE⊥AD,PF⊥CD,垂足分别是E,F.则PE+PF= .
13.如图,等边△DEC在正方形ABCD内,连接EA、EB,则∠AEB的度数是 .
14.如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F.若DE=,则BC的长为 .
三.解答题(共8小题,满分64分)
15.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
16.如图,菱形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,连接OE.
(1)求证:OE=CD;
(2)探究:当∠ABC等于多少度时,四边形OCED是正方形?并证明你的结论.
17.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
18.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
19.如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC的中点,延长DE到F,使得EF=DE,连接AF,CF.
(1)求证:四边形ADCF是菱形;
(2)请给△ABC添加一个条件,使得四边形ADCF是正方形,则添加的条件为 .
20.已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN.求证:MN=AM+CN.
21.如图,在△ABC中,∠BAC=90°,以BC为边,向外作正方形BCDE,对角线BD,CE交于点O.
(1)求证:∠ABO+∠ACO=180°;
(2)连接AO,用等式表示线段AB,AC,AO之间的数量关系,并证明你的结论.
22.如图,在正方形ABCD中,E为AB边上一点(不与点A,B重合),CF⊥DE于点G,交AD于点F,连接BG.
(1)求证:AE=DF;
(2)是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.
参考答案
一.选择题(共6小题,满分24分)
1.解:A、∵四边形ABCD是平行四边形,
又∵AB=BC,
∴四边形ABCD是菱形,故本选项不符合题意;
B、∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,故本选项不符合题意;
C、∵四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,故本选项不符合题意;
D、∵四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴四边形ABCD是矩形,不一定是正方形,故本选项符合题意;
故选:D.
2.解:连接CF,
∵正方形ABCD和正方形BEFG中,AB=7,BE=5,
∴GF=GB=5,BC=7,
∴GC=GB+BC=5+7=12,
∴CF===13,
∵M,N分别是DC,DF的中点,
∴MN=CF=,
故选:B.
3.解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°.
故选:A.
4.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣2,0),B(2,b),
∴OA=2,OM=2,
∴OD=AM=4,
∴AD===2,
∴正方形ABCD的面积=2×2=20,
故选:C.
5.解:连接DB,
∵四边形ABCD是正方形,AB=6,
∴∠A=90°,AD=AB=6,
∴DB===6,
∵点M,N分别是DQ,BQ的中点,
∴MN是△DQB的中位线,
∴MN=DB=3,
故选:A.
6.解:∵正方形ABCD的边长为,
∴OB=OC=BC=×=1,OB⊥OC,
∵CE=OC,
∴OE=2,
在Rt△OBE中,BE==.
故选:C.
二.填空题(共8小题,满分32分)
7.解:由于四边形ABCD是菱形,
如果∠BAD=90°,
那么四边形ABCD是正方形.
故答案为:∠BAD=90°.
8.解:∵正方形ABCD的面积为10,
∴AD2=10,
∴DH===1,
∵△AHD≌△DGC,
∴AH=DG=3,
∴HG=DG﹣DH=2,
∴正方形EFGH的面积=4,故答案为:4.
9.解:∵正方形ABCD的周长为16,
∴BC=4,
又∵O是正方形对角线的交点,
∴O是BD的中点,
∵H是CD边的中点,
∴OH是△DBC的中位线,
∴OH=BC=2.故答案为:2.
10.解:作MH⊥AC于H,如图,
∵四边形ABCD为正方形,
∴∠MAH=45°,
∴△AMH为等腰直角三角形,
∴AH=MH=AM=×4=2,
∵CM平分∠ACB,
∴BM=MH=2,
∴AB=4+2,
∴AC=AB=4+4,
∴OC=AC=2+2,CH=AC﹣AH=4+4﹣2=2+4,
∵BD⊥AC,
∴ON∥MH,
∴ON=2,故答案为:2;2.
11.解:作OE⊥OP交PD于点E,OF⊥PD于点F,设OC、PD交于点M,如图:
∵四边形ABCD是正方形,
∴OD=OC,∠DOC=90°,
∵CP⊥DP,
∴∠DPC=90°,
∴∠DOC=∠DPC,
又∵∠OMD=∠PMC,
∴∠ODE=∠OCP,
∵∠DOE+∠COE=90°,∠COP+∠COE=90°,
∴∠DOE=∠COP,
∴在△ODE和△OCP中,
,
∴△ODE≌△OCP(ASA).
∴OE=OP,DE=CP=5,
∴△OPE为等腰直角三角形,PE=DP﹣DE=7﹣5=2,
∵OF⊥PD,
∴EF=PF,
∴OF=PE=1,
∴△POD面积为:PD OF=.
故答案为:.
12.解:延长EP交BC于点G,
∵PE⊥AD,PF⊥CD,四边形ABCD是正方形,AC是对角线,
∴四边形EPFD是矩形,△PFC是等腰直角三角形,
∴EP=DF,PF=FC,
∴EP+PF=DF+FC=DC,
∵DC=2,
∴PE+PF=2,
故答案为:2.
13.解:由题意可知:AD=CD=DE=CE=CB,
∴∠EDC=60°,∠ADE=30°,
∴∠AED=∠BEC=75°,
∴∠AEB=360°﹣2∠AED﹣∠DEC=150°,
故答案为:150°
14.解:∵四边形ABCD为正方形,
∴∠C=90°,∠CDB=45°,BC=CD.
∴EC⊥CB.
又∵BE平分∠CBD,EF⊥BD,
∴EC=EF.
∵∠CDB=45°,EF⊥BD,
∴△DEF为等腰直角三角形.
∵DE=,
∴EF=1.
∴EC=1.
∴BC=CD=DE+EC=+1.
故答案为:+1.
三.解答题(共8小题,满分64分)
15.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)解:当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AE=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
故答案是:90°.
16.解:(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴∠COD=90°,AB=BC=CD=AD,
∴四边形OCED是矩形,
∴OE=DC;
(2)当∠ABC=90°时,四边形OCED是正方形,理由如下:
∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴DO=CO,
又∵四边形OCED是矩形,
∴四边形OCED是正方形.
17.(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8﹣6=2,CF=8+6=14,
在Rt△FCE中,EF===10.
18.解:(1)证明:∵四边形ABCD为正方形,
∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,
∴∠BFE=90°,∠BGE=90°.
又∵∠B=90°,
∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,
∴AB=40÷4=10cm.
∵四边形ABCD为正方形,
∴△AEF为等腰直角三角形,
∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,
∴当AF=5cm时,四边形BFEG是正方形.
19.(1)证明:
∵E为线段AC的中点,
∴AE=EC.
∵EF=DE
∴四边形ADCF是平行四边形.
又∵D为线段AB的中点,
∴DE∥BC,
∵∠AED=∠ACB=90°,
∴AC⊥FD.
∴平行四边形ADCF是菱形.
(2)CA=CB或∠B=45°,
∵CA=CB,AD=DB,
∴CD⊥AB,
∴∠CDA=90°,
∵ADCF是菱形,
∴ADCF是正方形.
故答案为:CA=CB或∠B=45°
20.证明:如图,
延长DC到E使CE=AM,连接BE,
∵正方形ABCD
∴AB=BC
∠A=∠ABC=∠BCD=90.
∴∠BCE=∠A=90°.
∴△ABM≌△CBE,
∴∠ABM=∠CBE,BM=BE
∵∠MBN=45°.
∴∠ABM+∠CBN=45°.
∴∠CBE+∠CBN=45°.
即∠EBN=∠MBN
∴△MBN≌△EBN,
∴MN=EN
∴MN=AM+CN.
21.(1)证明:∵四边形BCDE是正方形,
∴∠BOC=90°,
∵∠BAC=90°,
∴∠ABO+∠ACO=360°﹣∠BOC﹣∠BAC=360°﹣90°﹣90°=180°;
(2)解:线段AB,AC,AO之间的数量关系是:AC+AB=OA,证明如下:
延长AC到F,使CF=AB,连接OF、OA,如图:
由(1)知:∠ABO+∠ACO=180°,
而∠ACO+∠OCF=180°,
∴∠ABO=∠OCF,
∵四边形BCDE是正方形,
∴OB=OC,
在△AOB和△FOC中,
,
∴△AOB≌△FOC(SAS),
∴OA=OF,∠AOB=∠COF,
∵∠AOB+∠AOC=90°,
∴∠COF+∠AOC=90°,即∠AOF=90°,
∴△AOF是等腰直角三角形,
∴AF=OA,即AC+CF=OA,
∴AC+AB=OA.
22.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°,
∴∠ADE+∠AED=90°,
∵CF⊥DE于点G,
∴∠ADE+∠DFC=90°,
∴∠AED=∠DFC,
在△AED和△DFC中,
,
∴△AED≌△DFC(AAS),
∴AE=DF;
(2)解:存在,当点E为AB的中点时,△BCG为等腰三角形,
理由:如图,延长CB交DE的延长线于点P,
∵E为AB的中点,
∴AE=BE,
在△AED和△BEP中,
,
∴△AED≌△BEP(ASA),
∴AD=BP=BC,
∵∠PGC=90°,
∴BG=CP=BC,
即△BCG为等腰三角形.
一.选择题(共6小题,满分24分)
1.如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当AC=BD时,它是矩形
D.当∠ABC=90°时,它是正方形
2.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=( )
A. B. C.6 D.
3.如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
4.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣2,0),B(2,b),则正方形ABCD的面积是( )
A.34 B.25 C.20 D.16
5.如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=( )
A.3 B. C.3 D.6
6.如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为( )
A. B. C. D.2
二.填空题(共8小题,满分32分)
7.如图,四边形ABCD是菱形,AC与BD相交于点O,添加一个条件: ,可使它成为正方形.
8.用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形.若正方形ABCD的面积为10,AH=3,则正方形EFGH的面积为 .
9.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为16,则OH的长等于 .
10.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点.若AM=4,则BM= ,ON= .
11.如图,正方形ABCD对角线相交于点O,CP⊥DP于P,CP=5,DP=7,则△POD面积为 .
12.如图,正方形ABCD的边长为2,点P为对角线AC上任意一点.PE⊥AD,PF⊥CD,垂足分别是E,F.则PE+PF= .
13.如图,等边△DEC在正方形ABCD内,连接EA、EB,则∠AEB的度数是 .
14.如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F.若DE=,则BC的长为 .
三.解答题(共8小题,满分64分)
15.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
16.如图,菱形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,连接OE.
(1)求证:OE=CD;
(2)探究:当∠ABC等于多少度时,四边形OCED是正方形?并证明你的结论.
17.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
18.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
19.如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC的中点,延长DE到F,使得EF=DE,连接AF,CF.
(1)求证:四边形ADCF是菱形;
(2)请给△ABC添加一个条件,使得四边形ADCF是正方形,则添加的条件为 .
20.已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN.求证:MN=AM+CN.
21.如图,在△ABC中,∠BAC=90°,以BC为边,向外作正方形BCDE,对角线BD,CE交于点O.
(1)求证:∠ABO+∠ACO=180°;
(2)连接AO,用等式表示线段AB,AC,AO之间的数量关系,并证明你的结论.
22.如图,在正方形ABCD中,E为AB边上一点(不与点A,B重合),CF⊥DE于点G,交AD于点F,连接BG.
(1)求证:AE=DF;
(2)是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.
参考答案
一.选择题(共6小题,满分24分)
1.解:A、∵四边形ABCD是平行四边形,
又∵AB=BC,
∴四边形ABCD是菱形,故本选项不符合题意;
B、∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,故本选项不符合题意;
C、∵四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,故本选项不符合题意;
D、∵四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴四边形ABCD是矩形,不一定是正方形,故本选项符合题意;
故选:D.
2.解:连接CF,
∵正方形ABCD和正方形BEFG中,AB=7,BE=5,
∴GF=GB=5,BC=7,
∴GC=GB+BC=5+7=12,
∴CF===13,
∵M,N分别是DC,DF的中点,
∴MN=CF=,
故选:B.
3.解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°.
故选:A.
4.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣2,0),B(2,b),
∴OA=2,OM=2,
∴OD=AM=4,
∴AD===2,
∴正方形ABCD的面积=2×2=20,
故选:C.
5.解:连接DB,
∵四边形ABCD是正方形,AB=6,
∴∠A=90°,AD=AB=6,
∴DB===6,
∵点M,N分别是DQ,BQ的中点,
∴MN是△DQB的中位线,
∴MN=DB=3,
故选:A.
6.解:∵正方形ABCD的边长为,
∴OB=OC=BC=×=1,OB⊥OC,
∵CE=OC,
∴OE=2,
在Rt△OBE中,BE==.
故选:C.
二.填空题(共8小题,满分32分)
7.解:由于四边形ABCD是菱形,
如果∠BAD=90°,
那么四边形ABCD是正方形.
故答案为:∠BAD=90°.
8.解:∵正方形ABCD的面积为10,
∴AD2=10,
∴DH===1,
∵△AHD≌△DGC,
∴AH=DG=3,
∴HG=DG﹣DH=2,
∴正方形EFGH的面积=4,故答案为:4.
9.解:∵正方形ABCD的周长为16,
∴BC=4,
又∵O是正方形对角线的交点,
∴O是BD的中点,
∵H是CD边的中点,
∴OH是△DBC的中位线,
∴OH=BC=2.故答案为:2.
10.解:作MH⊥AC于H,如图,
∵四边形ABCD为正方形,
∴∠MAH=45°,
∴△AMH为等腰直角三角形,
∴AH=MH=AM=×4=2,
∵CM平分∠ACB,
∴BM=MH=2,
∴AB=4+2,
∴AC=AB=4+4,
∴OC=AC=2+2,CH=AC﹣AH=4+4﹣2=2+4,
∵BD⊥AC,
∴ON∥MH,
∴ON=2,故答案为:2;2.
11.解:作OE⊥OP交PD于点E,OF⊥PD于点F,设OC、PD交于点M,如图:
∵四边形ABCD是正方形,
∴OD=OC,∠DOC=90°,
∵CP⊥DP,
∴∠DPC=90°,
∴∠DOC=∠DPC,
又∵∠OMD=∠PMC,
∴∠ODE=∠OCP,
∵∠DOE+∠COE=90°,∠COP+∠COE=90°,
∴∠DOE=∠COP,
∴在△ODE和△OCP中,
,
∴△ODE≌△OCP(ASA).
∴OE=OP,DE=CP=5,
∴△OPE为等腰直角三角形,PE=DP﹣DE=7﹣5=2,
∵OF⊥PD,
∴EF=PF,
∴OF=PE=1,
∴△POD面积为:PD OF=.
故答案为:.
12.解:延长EP交BC于点G,
∵PE⊥AD,PF⊥CD,四边形ABCD是正方形,AC是对角线,
∴四边形EPFD是矩形,△PFC是等腰直角三角形,
∴EP=DF,PF=FC,
∴EP+PF=DF+FC=DC,
∵DC=2,
∴PE+PF=2,
故答案为:2.
13.解:由题意可知:AD=CD=DE=CE=CB,
∴∠EDC=60°,∠ADE=30°,
∴∠AED=∠BEC=75°,
∴∠AEB=360°﹣2∠AED﹣∠DEC=150°,
故答案为:150°
14.解:∵四边形ABCD为正方形,
∴∠C=90°,∠CDB=45°,BC=CD.
∴EC⊥CB.
又∵BE平分∠CBD,EF⊥BD,
∴EC=EF.
∵∠CDB=45°,EF⊥BD,
∴△DEF为等腰直角三角形.
∵DE=,
∴EF=1.
∴EC=1.
∴BC=CD=DE+EC=+1.
故答案为:+1.
三.解答题(共8小题,满分64分)
15.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)解:当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AE=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
故答案是:90°.
16.解:(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴∠COD=90°,AB=BC=CD=AD,
∴四边形OCED是矩形,
∴OE=DC;
(2)当∠ABC=90°时,四边形OCED是正方形,理由如下:
∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴DO=CO,
又∵四边形OCED是矩形,
∴四边形OCED是正方形.
17.(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8﹣6=2,CF=8+6=14,
在Rt△FCE中,EF===10.
18.解:(1)证明:∵四边形ABCD为正方形,
∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,
∴∠BFE=90°,∠BGE=90°.
又∵∠B=90°,
∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,
∴AB=40÷4=10cm.
∵四边形ABCD为正方形,
∴△AEF为等腰直角三角形,
∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,
∴当AF=5cm时,四边形BFEG是正方形.
19.(1)证明:
∵E为线段AC的中点,
∴AE=EC.
∵EF=DE
∴四边形ADCF是平行四边形.
又∵D为线段AB的中点,
∴DE∥BC,
∵∠AED=∠ACB=90°,
∴AC⊥FD.
∴平行四边形ADCF是菱形.
(2)CA=CB或∠B=45°,
∵CA=CB,AD=DB,
∴CD⊥AB,
∴∠CDA=90°,
∵ADCF是菱形,
∴ADCF是正方形.
故答案为:CA=CB或∠B=45°
20.证明:如图,
延长DC到E使CE=AM,连接BE,
∵正方形ABCD
∴AB=BC
∠A=∠ABC=∠BCD=90.
∴∠BCE=∠A=90°.
∴△ABM≌△CBE,
∴∠ABM=∠CBE,BM=BE
∵∠MBN=45°.
∴∠ABM+∠CBN=45°.
∴∠CBE+∠CBN=45°.
即∠EBN=∠MBN
∴△MBN≌△EBN,
∴MN=EN
∴MN=AM+CN.
21.(1)证明:∵四边形BCDE是正方形,
∴∠BOC=90°,
∵∠BAC=90°,
∴∠ABO+∠ACO=360°﹣∠BOC﹣∠BAC=360°﹣90°﹣90°=180°;
(2)解:线段AB,AC,AO之间的数量关系是:AC+AB=OA,证明如下:
延长AC到F,使CF=AB,连接OF、OA,如图:
由(1)知:∠ABO+∠ACO=180°,
而∠ACO+∠OCF=180°,
∴∠ABO=∠OCF,
∵四边形BCDE是正方形,
∴OB=OC,
在△AOB和△FOC中,
,
∴△AOB≌△FOC(SAS),
∴OA=OF,∠AOB=∠COF,
∵∠AOB+∠AOC=90°,
∴∠COF+∠AOC=90°,即∠AOF=90°,
∴△AOF是等腰直角三角形,
∴AF=OA,即AC+CF=OA,
∴AC+AB=OA.
22.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°,
∴∠ADE+∠AED=90°,
∵CF⊥DE于点G,
∴∠ADE+∠DFC=90°,
∴∠AED=∠DFC,
在△AED和△DFC中,
,
∴△AED≌△DFC(AAS),
∴AE=DF;
(2)解:存在,当点E为AB的中点时,△BCG为等腰三角形,
理由:如图,延长CB交DE的延长线于点P,
∵E为AB的中点,
∴AE=BE,
在△AED和△BEP中,
,
∴△AED≌△BEP(ASA),
∴AD=BP=BC,
∵∠PGC=90°,
∴BG=CP=BC,
即△BCG为等腰三角形.
