第18章平行四边形练习题2020-2021年黑龙江各地八年级下学期期末数学(人教版)试题选编(Word版含解析)
文档属性
| 名称 | 第18章平行四边形练习题2020-2021年黑龙江各地八年级下学期期末数学(人教版)试题选编(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 20:19:58 | ||
图片预览



文档简介
第18章:平行四边形练习题
一、单选题
1.(2021·黑龙江龙凤·八年级期末)如图,在平行四边形ABCD中,下列各式不一定正确的是( )
A. B.
C. D.
2.(2021·黑龙江碾子山·八年级期末)如图,在平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
3.(2021·黑龙江萝北·八年级期末)如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.3和2 B.2和3 C.4和1 D.1和4
4.(2021·黑龙江绥滨·八年级期末)如图,在中,平分,则的长是( )
A. B.
C. D.
5.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)在平行四边形ABCD中,若∠A∶∠B=5∶4,则∠C的度数为( )
A.80° B.120° C.100° D.110°
6.(2021·黑龙江南岗·八年级期末)若中,,则的度数为( ).A. B. C. D.
7.(2021·黑龙江巴彦·八年级期末)如的对角线与相较于,,若,,则长( )
A.6 B.10 C.12 D.18
8.(2021·黑龙江勃利·八年级期末)如图,平行四边形ABCD中,AD=5,AB=3,BE 平分∠ABC交AD边于点E,则线段AE、ED的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
9.(2021·黑龙江林口·八年级期末)下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠C,∠B=∠D
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
10.(2021·黑龙江龙凤·八年级期末)下列说法中,不正确是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行另一组对边相等的四边形是平行四边形
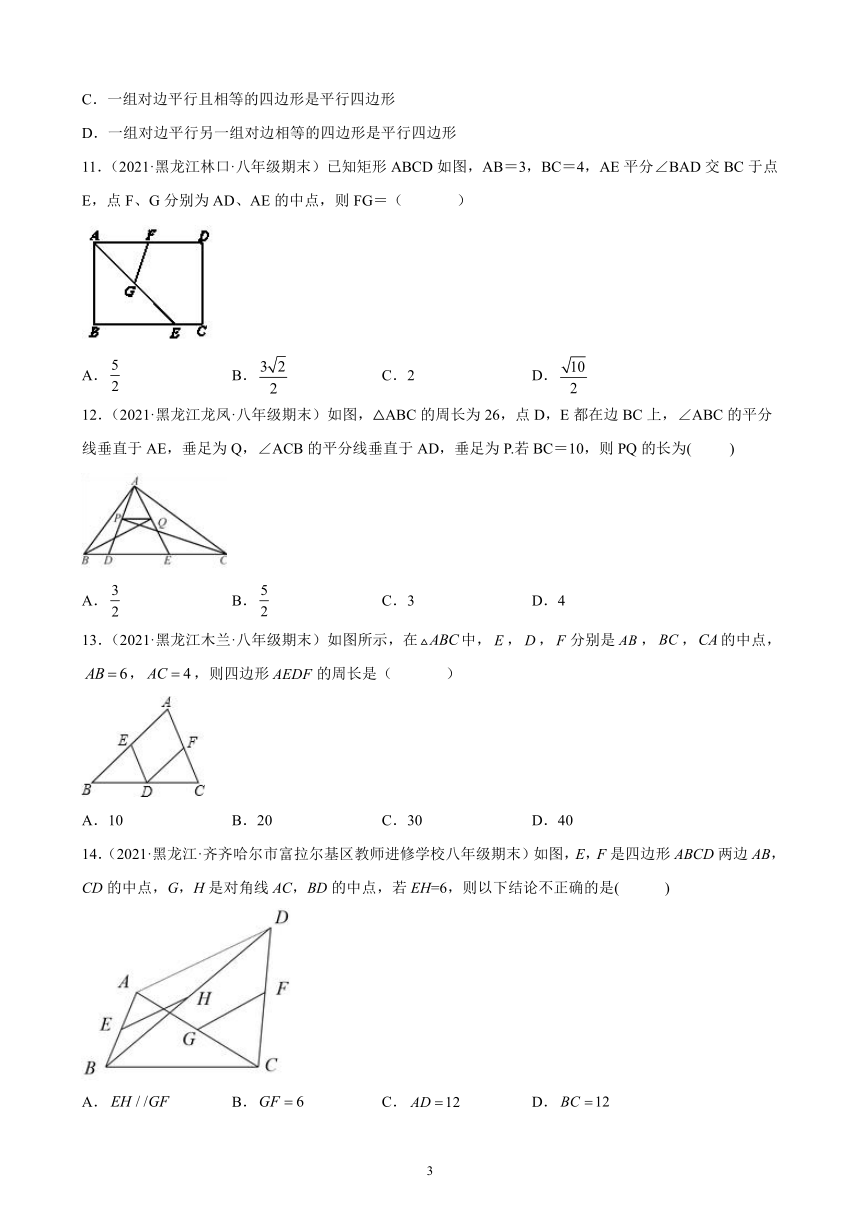
11.(2021·黑龙江林口·八年级期末)已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A. B. C.2 D.
12.(2021·黑龙江龙凤·八年级期末)如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长为( )
A. B. C.3 D.4
13.(2021·黑龙江木兰·八年级期末)如图所示,在中,,,分别是,,的中点,,,则四边形的周长是( )
A.10 B.20 C.30 D.40
14.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)如图,E,F是四边形ABCD两边AB,CD的中点,G,H是对角线AC,BD的中点,若EH=6,则以下结论不正确的是( )
A. B. C. D.
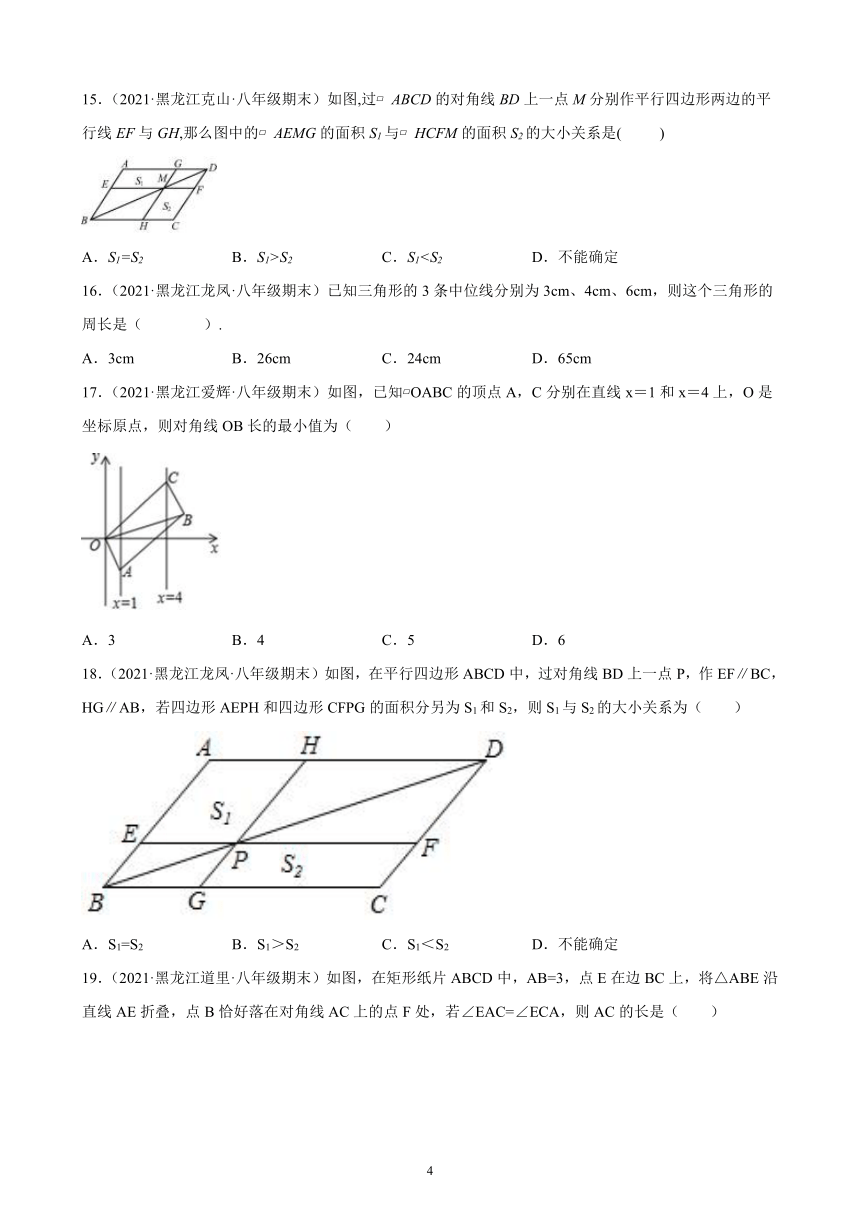
15.(2021·黑龙江克山·八年级期末)如图,过 ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG的面积S1与 HCFM的面积S2的大小关系是( )
A.S1=S2 B.S1>S2 C.S116.(2021·黑龙江龙凤·八年级期末)已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( ).
A.3cm B.26cm C.24cm D.65cm
17.(2021·黑龙江爱辉·八年级期末)如图,已知 OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A.3 B.4 C.5 D.6
18.(2021·黑龙江龙凤·八年级期末)如图,在平行四边形ABCD中,过对角线BD上一点P,作EF∥BC,HG∥AB,若四边形AEPH和四边形CFPG的面积分另为S1和S2,则S1与S2的大小关系为( )
A.S1=S2 B.S1>S2 C.S1<S2 D.不能确定
19.(2021·黑龙江道里·八年级期末)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A. B.6 C.4 D.5
20.(2021·黑龙江道外·八年级期末)如图,在矩形纸片ABCD中,AB=6,AD=8,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则线段EF的长为( )
A.3 B.4 C.5 D.6
21.(2021·黑龙江绥棱·八年级期末)如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF,其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
22.(2021·黑龙江克山·八年级期末)如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A.30° B.45° C.60° D.75°
23.(2021·黑龙江林口·八年级期末)如图,将一张矩形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是( )
A.112° B.136° C.144° D.158°
24.(2021·黑龙江勃利·八年级期末)如图,矩形中,,,在数轴上,若以点A为圆心,对角线的长为半径作弧交数轴于点M,则点M表示的数为( )
A.2 B. C. D.
25.(2021·黑龙江铁锋·八年级期末)如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
A.下滑时,OP增大 B.上升时,OP减小
C.无论怎样滑动,OP不变 D.只要滑动,OP就变化
26.(2021·黑龙江铁锋·八年级期末)在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
27.(2021·黑龙江集贤·八年级期末)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
A.20° B.25° C.30° D.40°
28.(2021·黑龙江讷河·八年级期末)如图,在菱形中,P是对角线上一动点,过点P作于点E.于点F.若菱形的周长为20,面积为24,则的值为( )
A.4 B. C.6 D.
29.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)矩形具有而菱形不具有的性质是【 】
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
30.(2021·黑龙江绥棱·八年级期末)已知四边形是平行四边形,下列结论中不正确的是( )
A.当时,它是菱形 B.当时,它是正方形
C.当时,它是矩形 D.当时,它是菱形
31.(2021·黑龙江昂昂溪·八年级期末)如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法判断
32.(2021·黑龙江昂昂溪·八年级期末)如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是( )
A.3 B.2 C.3 D.6
33.(2021·黑龙江绥滨·八年级期末)如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①②③
34.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)如图,在中,点E为边DC上一点,连接AE,将沿AE翻折,点D的对应点落在边AB上,,,则边BC的长是( )
A.5 B.6 C.7 D.8
35.(2021·黑龙江木兰·八年级期末)如图.正方形和正方形中,点在上,,,是的中点,那么的长是( ).
A. B. C. D.2
36.(2021·黑龙江爱辉·八年级期末)正方形具有而菱形不一定具有的性质是( )
A.四条边都相等 B.对角线互相垂直且平分
C.对角线相等 D.对角线平分一组对角
37.(2021·黑龙江道里·八年级期末)下列命题错误的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.对角线互相垂直的矩形是正方形
38.(2021·黑龙江牡丹江·八年级期末)如图,四边形是正方形,线段交于点,连接,,点在线段上,,于.下列结论:①;②;③平分;④;⑤若,则,其中正确结论的个数是( )
A. B. C. D.
39.(2021·黑龙江铁锋·八年级期末)如图,已知在正方形ABCD中,厘米,,点E在边AB上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动时间为t秒.若存在a与t的值,使与全等时,则t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
40.(2021·黑龙江南岗·八年级期末)下列命题中,假命题的是( )
A.四个角都相等的四边形是矩形
B.对角线互相平分且垂直的四边形是菱形
C.对角线互相垂直且相等的四边形是正方形
D.对角线相等的平行四边形是矩形
41.(2021·黑龙江昂昂溪·八年级期末)如图,正方形的面积为,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( ).
A. B. C. D.
二、填空题
42.(2021·黑龙江龙凤·八年级期末)如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
43.(2021·黑龙江集贤·八年级期末)如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________(只添一个即可),使四边形ABCD是平行四边形.
44.(2021·黑龙江林口·八年级期末)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线交于点.若,则__________.
45.(2021·黑龙江南岗·八年级期末)如图,,是正方形的对角线上的两点,,,则四边形的周长是_____.
46.(2021·黑龙江集贤·八年级期末)矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为_____________.
47.(2021·黑龙江讷河·八年级期末)如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件:___,使得平行四边形ABCD为菱形.
48.(2021·黑龙江绥棱·八年级期末)已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=___.
49.(2021·黑龙江绥滨·八年级期末)如图,将菱形纸片ABCD折迭,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2 cm,∠A=120°,则EF=_______cm.
50.(2021·黑龙江绥滨·八年级期末)如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为_____.
51.(2021·黑龙江·肇州县教师进修学校八年级期末)如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是__.
52.(2021·黑龙江南岗·八年级期末)若菱形的两条对角线长分别是6㎝和8㎝,则该菱形的面积是____㎝2.
53.(2021·黑龙江绥棱·八年级期末)如图, ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为______cm.
三、解答题
54.(2021·黑龙江林口·八年级期末)△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF,
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB=2,CD=BC,请求出GE的长.
55.(2021·黑龙江昂昂溪·八年级期末)如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D.
求证:(1)AE=CD.(2)若AC=12cm,求BD的长.
56.(2021·黑龙江绥滨·八年级期末)如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AMBE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AMBE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗.如果成立,请给出证明;如果不成立,请说明理由.
57.(2021·黑龙江绥棱·八年级期末)如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
58.(2021·黑龙江·五常市教师进修学校八年级期末)如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为__________°.
59.(2021·黑龙江龙凤·八年级期末)已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.
(1)求证:△BAD≌△CAE;
(2)若∠ABC=30°,求∠MEC的度数;
(3)求证:四边形MBDE是平行四边形.
60.(2021·黑龙江昂昂溪·八年级期末)综合与实践
(1)问题发现:正方形ABCD和等腰直角△BEF按如图①所示的方式放置,点F在AB上,连接AE、CF,则AE、CF的数量关系为 ,位置关系为 .
(2)类比探究:正方形ABCD保持固定,等腰直角△BEF绕点B顺时针旋转,旋转角为α(0°<α ≤360°),请问(1)中的结论还成立吗?请就图②说明你的理由:
(3)拓展延伸:在(2)的条件下,若AB= 2 BF= 4,在等腰直角△BEF旋转的过程中,当CF为最大值时,请直接写出DE的长.
61.(2021·黑龙江绥棱·八年级期末)已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:;
(2)连接AC,DE,当 四边形ACED是正方形?请说明理由.
62.(2021·黑龙江·五常市教师进修学校八年级期末)在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC,
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
63.(2021·黑龙江龙凤·八年级期末)如图,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形.
(2)求四边形ABCE的面积.
64.(2021·黑龙江铁锋·八年级期末)如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.
(1)求证:四边形CFBD是菱形;
(2)连接AE,若CF=,DF=2,求AE的长.
65.(2021·黑龙江萝北·八年级期末)如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.
(1)求证:△ADE≌△CBF;
(2)判定四边形DEBF是否是平行四边形?
66.(2021·黑龙江集贤·八年级期末)如图,在中,,,,点从点出发沿方向以4cm/s的是速度向点匀速运动,同时点从出发沿方向以2cm/s的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点、运动的时间是s.过点作于点,连接、.
(1)求证:;
(2)四边形能够成为菱形吗?如果能,求出相应的值;如果不能,请说明理由;
(3)当为何值时,为直角三角形?请说明理由.
67.(2021·黑龙江木兰·八年级期末)如图,在中,,点在对角线上,,于点,的延长线交于点.点在的延长线上,且,连接.
(1)若,,求的长;
(2)求证:.
68.(2021·黑龙江牡丹江·八年级期末)如图,已知等腰,,平分,为上一动点,作平行,交于F,在上取一点,使得,连接.
(1)根据题意补全图形;
(2)求证四边形是平行四边形;
(3)若,写出一个的度数,使得四边形是菱形.
试卷第1页,共3页
参考答案:
1.D
【详解】
由 ABCD的性质及图形可知:
A、∠1和∠2是邻补角,故∠1+∠2=180°,正确;
B、因为AD∥BC,所以∠2+∠3=180°,正确;
C、因为AB∥CD,所以∠3+∠4=180°,正确;
D、根据平行四边形的对角相等,∠2=∠4,∠2+∠4=180°不一定正确;
故选D.
2.B
【分析】
由AC的垂直平分线交AD于E,易证得AE=CE,又由四边形ABCD是平行四边形,即可求得AD与DC的长,继而求得答案.
【详解】
解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,
∴△CDE的周长是:DC+DE+CE=DC+DE+AE=DC+AD=3+5=8,
故选B.
【点睛】
此题考查线段垂直平分线的性质,平行四边形的性质,解题关键在于得到AE=CE.
3.A
【分析】
利用平行四边形的性质、角平分线的性质和等腰三角形的性质可得AD=BC,BE= AB,然后根据EC=BC-BE即可.
【详解】
解:∵AE平分∠BAD
∴∠BAE=∠DAE
∵四边形ABCD是平行四边形
∴AD//BC,AD=BC
∴∠DAE=∠AEB
∴∠BAE=∠BEA
∴AB=BE=3
∴EC=AD-BE=2
故答案为A.
【点睛】
本题主要考查了平行四边形性质及等腰三角形的性质,根据题意说明△ABE是解答本题的关键.
4.C
【分析】
根据平行四边形的性质得出AB=CD,AD=BC=6,AD∥BC,根据平行线性质求出∠ADE=∠DEC,根据角平分线定义求出∠ADE=∠CDE,推出∠CDE=∠DEC,推出CE=DC,求出CD即可.
【详解】
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=6,AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴CE=DC,
∵BC=6,BE=2,
∴CD=CE=6-2=4,
故选:C.
【点睛】
本题考查了平行四边形的性质,角平分线定义,平行线的性质,等腰三角形的性质和判定的应用,解题的关键是求出CD的长,注意:平行四边形的对边平行且相等,难度适中.
5.C
【分析】
根据平行四边形的性质可知∠A,∠B互补,再根据已知可以求出∠A,∠B的度数,而∠C是∠A的对角,所以相等即可得出答案.
【详解】
解:∵四边形ABCD是平行四边形
∴AD//BC,∠A=∠C
∴∠A+∠B=180°,
∵∠A:∠B=5:4
∴∠A=100°,∠B=80°
∴∠C=∠A=100°.
故选:C.
【点睛】
本题主要考查了平行四边形的性质;①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.
6.A
【分析】
根据平行四边形对角相等即可求解.
【详解】
解:∵平行四边形ABCD中,∠A=38°,
∴∠C=∠A=38°,
故选A.
【点睛】
本题考查了平行四边形的应用,熟练掌握平行四边形对角相等的性质是解题关键.
7.C
【分析】
利用平行四边形的性质和勾股定理易求AO的长,进而可求出AC的长.
【详解】
解:∵ ABCD的对角线AC与BD相交于点O,
∴,,
∵AB⊥AC,
∴∠BAO=90°,
∴,
∴AC=2AO=12,
故选C.
【点睛】
本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.
8.B
【分析】
根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得DE的长度.
【详解】
解:∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC=5,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3,
∴DE=AD﹣AE=5﹣3=2
故选B.
【点睛】
本题主要考查了平行四边形的性质,角平分线的性质,解题的关键在于能够熟练掌握相关性质进行求解.
9.A
【分析】
直接根据平行四边形的判定定理判断即可.
【详解】
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断;
平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴B能判断;
平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴D能判定;
平行四边形判定定理3,对角线互相平分的四边形是平行四边形;
平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;
故选A.
【点睛】
此题是平行四边形的判定,解本题的关键是掌握和灵活运用平行四边形的5个判断方法.
10.D
【分析】
由平行四边形的判定方法得出A、B、C正确;即可得出结论.
【详解】
解:∵对角线互相平分的四边形是平行四边形,
∴A正确;
∵两组对角分别相等的四边形是平行四边形,
∴B正确;
∵一组对边且相等的四边形是平行四边形,
∴C正确;
∵一组对边平行另一组对边相等的四边形是等腰梯形,不一定是平行四边形,
∴D不正确.
故选D.
【点睛】
本题考查了平行四边形的判定方法:熟练掌握平行四边形的判定方法,并能进行推理论证是解决问题的关键.
11.D
【分析】
由AE平分∠BAD得∠BAE=∠DAE,根据矩形ABCD可得△ABE是等腰直角三角形,所以BE=AB=3,从而可求EC=1,连接DE,由勾股定理得DE的长,再根据三角形中位线定理可求FG的长.
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE=3,
∵BC=AD=4,
∴EC=1,
连接DE,如图,
∴DE=,
∵点F、G分别为AD、AE的中点,
∴FG=.
故选D.
【点睛】
本题考查了矩形的性质以及三角形中位线定理,熟记性质与定理是解题关键.
12.C
【详解】
首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为26,及BC=10,可得DE=6,利用中位线定理可求出PQ.
13.A
【分析】
根据三角形的中位线平行于第三边,并且等于第三边的一半,以及中点的定义可得,,再根据四边形的周长的定义计算即可得解
【详解】
解:在中,、、分别是、、的中点,
,,
四边形的周长是.
故选:.
【点睛】
本题考查了三角形中位线定理,中点的定义以及四边形周长的定义,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.
14.D
【分析】
由三角形中位线定理可得EH∥AD,EH=AD,GF∥AD,GF=AD,可得EH∥GF,EH=GF=6,AD=2EH=12,利用排除法可求解.
【详解】
解:∵E、F是AB、CD的中点,G、H是AC、BD的中点,
∴EH∥AD,EH=AD,GF∥AD,GF=AD,
∴EH∥GF,EH=GF=6,
∴AD=2EH=12,
故选:D.
【点睛】
本题考查了三角形中位线定理,掌握三角形的中位线定理是本题的关键.
15.A
【分析】
根据平行四边形的性质和判定得出平行四边形GBEP、GPFD,证△ABD≌△CDB,得出△ABD和△CDB的面积相等;同理得出△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,相减即可求出答案.
【详解】
∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
∵
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故选A.
【点睛】
本题考查了平行四边形的性质和判定,全等三角形的性质和判定的应用,解此题的关键是求出△ABD和△CDB的面积相等,△BEP和△PGB的面积相等,△HPD和△FDP的面积相等,注意:如果两三角形全等,那么这两个三角形的面积相等
16.B
【详解】
如图所示:
∵D,E,F分别是△ABC的三边的中点,
∴DE= AC,DF=BC,EF=AB,
∴AC+BC+AB=2(DE+DF+EF)=2×(3+4+6)=26(cm).
故选B.
17.C
【分析】
过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E.则OB=.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.
【详解】
解:过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,
,
∴△OAF≌△BCD.
∴BD=OF=1,
∴OE=4+1=5,
∴OB=.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=5.
故选:C.
【点睛】
本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
18.A
【详解】
试题分析:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形GBEP、HPFD是平行四边形,
∵在△ABD和△CDB中,AB=CD,BD=BD,AD=BC,
∴△ABD≌△CDB,
即△ABD和△CDB的面积相等;
同理△BEP和△PGB的面积相等,△HPD和△FDP的面积相等,
∴四边形AEPH和四边形CFPG的面积相等,即S1=S2.
故选A.
考点:1.平行四边形的判定与性质2.全等三角形的判定与性质.
19.B
【详解】
∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,
∴AF=AB,∠AFE=∠B=90°,
∴EF⊥AC,
∵∠EAC=∠ECA,
∴AE=CE,
∴AF=CF,
∴AC=2AB=6,
故选B.
【点睛】本题考查了翻折变换的性质、矩形的性质等,得到EF垂直平分AC是解题的关键.
20.A
【分析】
根据矩形的性质可得BC=AD,∠B=90°,利用勾股定理可求出AC的长,根据折叠的性质可得AF=AB,∠B=∠AFE=90°,BE=EF,在Rt△CEF中利用勾股定理列方程求出EF的长即可得答案.
【详解】
∵四边形ABCD是矩形,AD=8,
∴∠B=90°,BC=AD=8,
∴AC==10,
∵折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,
∴BE=EF,AF=AB=6,∠AFE=∠B=90°,
∴CF=AC-AF=10﹣6=4,
在Rt△CEF中,由勾股定理得,EF2+CF2=CE2,
∴EF2+CF2=(BC-EF)2,即EF2+42=(8-EF)2,
解得:EF=3,
故选:A.
【点睛】
本题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.
21.B
【详解】
试题分析:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF.
由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC.
∵BF平分∠EBC,∴CF=MF.∴DF=CF.故①正确.
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC.
∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN.
∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN.故②正确.
∵在△DEF和△CNF中,易由ASA得△DEF≌△CNF,∴EF=FN.∴BE=BN.
但无法求得△BEN各角的度数,
∴△BEN不一定是等边三角形.故③错误.
∵∠BEM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM.∴BM=3EM.
∴S△BEF=3S△EMF=3S△DEF.故④正确.
综上所述,正确的结论是①②④.故选B.
22.C
【详解】
如图所示:
由题意可得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=AM,故AN=NG,
则∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=×90°=30°,
∴∠DAG=60°.
故选C.
23.B
【分析】
由AD//BC,∠EFG=68°,根据两直线平行,内错角相等,可求得∠DEF的度数,然后由折叠的性质,求得∠DEG的度数,继而求得答案.
【详解】
解:∵AD//BC,∠EFG=68°,
∴∠DEF=∠EFG=68°,
由折叠的性质可得:∠FEG=∠DEF=68°,
∴∠DEG=∠DEF+∠FEG=136°,
∵AD//BC,
∴∠1=∠DEG=136°.
故选:B.
【点睛】
此题考查了平行线的性质以及折叠的性质.注意掌握折叠前后图形的对应关系是解此题的关键.
24.C
【分析】
首先根据勾股定理计算出AC的长,进而得到AM的长,再根据A点表示-1,可得M点表示的数.
【详解】
解:∵矩形中,,,
∴,,
∴,
∴,
∵A点表示-1,
∴M点表示的数为:
故选:C.
【点睛】
此题主要考查了勾股定理和数轴的应用,矩形的性质,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
25.C
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得OP=AB.
【详解】
解:∵AO⊥BO,点P是AB的中点,
∴OP=AB,
∴在滑动的过程中OP的长度不变.
故选:C.
【点睛】
本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.
26.C
【分析】
根据矩形的判定条件逐项进行分析判断即可;
【详解】
解:A、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项B符合题意;
C、∵AD∥BC,
∴∠A+∠B=∠C+∠D=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,AB=CD,故选项C不符合题意;
D、∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴AB⊥AD,AB⊥BC,AB的长为AD、BC间的距离,
又∵AB=CD,
∴CD⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形,
∴选项D不符合题意;
故选:C.
【点睛】
本题主要考查了矩形的判定,准确分析判断是解题的关键.
27.A
【分析】
先根据菱形的性质得OD=OB,AB∥CD,BD⊥AC,则利用DH⊥AB得到DH⊥CD,∠DHB=90°,所以OH为Rt△DHB的斜边DB上的中线,得到OH=OD=OB,利用等腰三角形的性质得∠1=∠DHO,然后利用等角的余角相等即可求出∠DHO的度数.
【详解】
解:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠1=∠DHO,
∵DH⊥CD,
∴∠1+∠2=90°,
∵BD⊥AC,
∴∠2+∠DCO=90°,
∴∠1=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=20°,
∴∠DHO=20°,
故选A.
【点睛】
本题考查菱形的性质,直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
28.B
【分析】
连接BP,通过菱形的周长为20,求出边长,菱形面积为24,求出SABC的面积,然后利用面积法,SABP+SCBP=SABC,即可求出的值.
【详解】
解:连接BP,
∵菱形ABCD的周长为20,
∴AB=BC=20÷4=5,
又∵菱形ABCD的面积为24,
∴SABC=24÷2=12,
又SABC= SABP+SCBP
∴SABP+SCBP=12,
∴ ,
∵AB=BC,
∴
∵AB=5,
∴PE+PF=12×=.
故选:B.
【点睛】
本题主要考查菱形的性质,解题关键在于添加辅助线,通过面积法得出等量关系,求出PF+PE的值.
29.B
【详解】
根据矩形与菱形的性质对各选项解析判断后利用排除法求解:
A.矩形与菱形的两组对边都分别平行,故本选项错误;
B.矩形的对角线相等,菱形的对角线不相等,故本选项正确;
C.矩形与菱形的对角线都互相平分,故本选项错误;
D.矩形与菱形的两组对角都分别相等,故本选项错误.
故选B.
30.B
【分析】
根据菱形、正方形、矩形的判定方法一一判断即可.
【详解】
解:A、正确.根据邻边相等的平行四边形是菱形;
B、错误.对角线相等的四边形是矩形,不一定是正方形.
C、正确.有一个角是直角的平行四边形是矩形.
D、正确.对角线垂直的平行四边形是菱形.
故选:B.
【点睛】
此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,属于基础题.
31.B
【分析】
作DF⊥BC,BE⊥CD,先证四边形ABCD是平行四边形.再证Rt△BEC≌Rt△DFC,得,BC=DC,所以,四边形ABCD是菱形.
【详解】
如图,作DF⊥BC,BE⊥CD,
由已知可得,AD∥BC,AB∥CD
∴四边形ABCD是平行四边形.
在Rt△BEC和Rt△DFC中
∴Rt△BEC≌Rt△DFC,
∴BC=DC
∴四边形ABCD是菱形.
故选B
【点睛】
本题考核知识点:菱形的判定.解题关键点:通过全等三角形证一组邻边相等.
32.C
【分析】
首先连接AC,交BD于点O,连接CM,则CM与BD交于点P,此时PA+PM的值最小,由在菱形ABCD中,AB=6,∠ABC=60°,易得△ACD是等边三角形,BD垂直平分AC,继而可得CM⊥AD,则可求得CM的值,继而求得PA+PM的最小值.
【详解】
解:连接AC,交BD于点O,连接CM,则CM与BD交于点P,此时PA+PM的值最小,
∵在菱形ABCD中,AB=6,∠ABC=60°,
∴∠ADC=∠ABC=60°,AD=CD=6,BD垂直平分AC,
∴△ACD是等边三角形,PA=PC,
∵M为AD中点,
∴DM=AD=3,CM⊥AD,
∴CM==3,
∴PA+PM=PC+PM=CM=3.
故选C.
【点睛】
此题考查了最短路径问题、等边三角形的判定与性质、勾股定理以及菱形的性质.注意准确找到点P的位置是解此题的关键.
33.A
【分析】
菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形.据此判断即可.
【详解】
解:① ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定 ABCD是菱形;故①正确;
② ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故②错误;
③ ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定 ABCD是菱形;故③正确;
D、 ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故④错误.
故选:A.
【点睛】
此题考查了菱形的判定与矩形的判定定理.此题难度不大,注意掌握菱形的判定定理是解此题的关键.
34.A
【分析】
通过证明四边形ADED'是菱形,可得AE⊥DD',AO=EO=4,DO=D'O=3,由勾股定理可求AD的长,即可求BC的长.
【详解】
如图,设AE与的交点为.
∵四边形ABCD是平行四边形,
∴,.
∵将沿AE翻折,
,,.
∵,
∴,
∴,
∴,
∴
∴四边形是菱形,
则,,,
∴,
∴.
故选:A.
【点睛】
本题考查了翻折变换,平行四边形的性质,菱形的判定和性质,勾股定理,证明四边形ADED'是菱形是本题的关键.
35.B
【分析】
连接AC、CF,如图,根据正方形的性质得∠ACD=45°,∠FCG=45°,AC=,CF=3,则∠ACF=90°,再利用勾股定理计算出AF=2,然后根据直角三角形斜边上的中线求CH的长.
【详解】
解:连接AC、CF,如图,
∵四边形ABCD和四边形CEFG都是正方形,
∴∠ACD=45°,∠FCG=45°,AC=BC=,CF=CE=3,
∴∠ACF=45°+45°=90°,
在Rt△ACF中,AF=,
∵H是AF的中点,
∴CH=AF=.
故选:B.
【点睛】
本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.两条对角线将正方形分成四个全等的等腰直角三角形.也考查了直角三角形斜边上的中线性质.
36.C
【分析】
根据正方形和菱形的性质逐项判断即可得.
【详解】
A、正方形和菱形的四条边都相等,则此项不符题意;
B、正方形和菱形的对角线都互相垂直且平分,则此项不符题意;
C、正方形的对角线相等,而菱形的对角线不一定相等,则此项符合题意;
D、正方形和菱形的对角线都平分一组对角,则此项不符题意;
故选:C.
【点睛】
本题考查了正方形和菱形的性质,熟练掌握正方形和菱形的性质是解题关键.
37.C
【详解】
解:A、对角线互相平分的四边形是平行四边形,正确,不符合题意;
B、对角线相等的平行四边形是矩形,正确,不符合题意;
C、一条对角线平分一组对角的四边形可能是菱形或者正方形,错误,符合题意;
D、对角线互相垂直的矩形是正方形,正确,不符合题意,
故选C.
【点睛】
本题考查命题与定理.
38.A
【分析】
①根据正方形的性质可得AD=AB,由AD=DE可求出AB=DE;过点D作DH⊥AE,根据等腰三角形的性质可得AH=,②再利用全等三角形的判定可得,由全等三角形的性质可得AH=BN,继而可得BN=;由∠AFD=45°可得∠FDH=45°,③∠FDE+∠EDH=45°,∠CDF+∠ADH=45°,从而可得∠CDF=∠FDE,继而求出DF平分∠CDE;④根据,即可得,根据,即可证明;⑤由条件可得为的角平分线,根据角平分线的性质,以及三角形的面积之比可得与的比,进而求解.
【详解】
解:①∵正方形ABCD,
∴AD=AB,
∵AD=DE,
∴AB=DE,故①正确;
②过点D作DH⊥AE,
∵AD=DE,
∴AH=,
∵∠DAH+∠BAE=90°,∠DAH+∠ADH=90°,
∴∠BAE=∠ADH,
在和中,
∵∠ANB=∠DHA=90°,∠BAN=∠ADH,AB=AD,
∴,
∴AH=BN,
∴BN=,故②正确;
③过点D作DH⊥AE,
∵AD=DE,
∴AH平分∠ADE,
∴∠EDH=∠ADH,
∵∠AFD=45°,∠DHF=90°,
∴∠FDH=45°,
∴∠FDE+∠EDH=45°,
又∵∠ADC=90°,
∴∠CDF+∠ADH=45°,
∴∠CDF=∠FDE,
∴DF平分∠CDE,故③正确;
④
,
即
故④正确
⑤若,
则
四边形是正方形
即为的角平分线
如图,过点作
.
故⑤正确.
故正确的有①②③④⑤,共5个
故选A
【点睛】
本题主要考查正方形的性质和全等三角形的判定与性质,等腰三角形的性质,角平分线性质,解决本题的关键是要熟练掌握正方形的性质和全等三角形的判定.
39.D
【分析】
根据题意分两种情况讨论若△BPE≌△CQP,则BP=CQ,BE=CP;若△BPE≌△CPQ,则BP=CP=5厘米,BE=CQ=6厘米进行求解即可.
【详解】
解:当,即点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∴BP=10-6=4厘米,
∴运动时间t=4÷2=2(秒);
当,即点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t=(秒).
综上t的值为2.5或2.
故选:D.
【点睛】
本题主要考查正方形的性质以及全等三角形的判定,解决问题的关键是掌握正方形的四条边都相等,四个角都是直角;两边及其夹角分别对应相等的两个三角形全等.同时要注意分类思想的运用.
40.C
【分析】
根据平行四边形,矩形,菱形和正方形的判定进行判断即可.
【详解】
解:A、四边形的内角和为360°,
∵四个角都相等,
∴四边形的每个角都等于90°,
∴此四边形是矩形,
故该命题是真命题;
B、对角线互相平分的四边形是平行四边形,
对角线垂直的平行四边形是菱形,
故该命题是真命题;
C、对角线互相平分、互相垂直且相等的四边形才是正方形,
故该命题是假命题;
D、对角线相等的平行四边形是矩形,是真命题.
故选C.
【点睛】
本题考查了从对角线来判断特殊四边形的方法:对角线互相平分的四边形为平行四边形;对角线互相垂直平分的四边形为菱形;对角线互相平分且相等的四边形为矩形;对角线互相垂直平分且相等的四边形为正方形.
41.C
【详解】
连接、、关于对称.
∴.
∴,当、、三点共线得最小.
∴,选.
点睛:本题考查的是正方的性质和轴对称-最短线题,熟知“两点之间,线段最短”是解答此的关键.
42.48
【分析】
首先根据平行四边形的性质可得AB=CD,AD=BC,可得AB+BC=20,再利用其面积的求法S=BC×AE=CD×AF,可得4AE=6CD,列出方程组,求出平行四边形的各边长,再求其面积.
【详解】
解:设BC=x,CD=y,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵ ABCD的周长为40,
∴x+y=20,
∵AE=4,AF=6,S=BC×AE=CD×AF,
∴4x=6y,
得方程组:,
解得:
∴S平行四边形ABCD=BC×AE=12×4=48.
故答案为:48.
【点睛】
此题主要考查了平行四边形的性质与其面积公式,解题的关键是根据性质得到邻边的和,根据面积公式得到方程,再解方程组即可.
43.BO=DO.
【详解】
解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
故答案为BO=DO.
44.20
【分析】
由垂美四边形的定义可得AC⊥BD,再利用勾股定理得到AD2+BC2=AB2+CD2,从而求解.
【详解】
∵四边形ABCD是垂美四边形,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2,
∵AD=2,BC=4,
∴AD2+BC2=22+42=20,
故答案为:20.
【点睛】
本题主要考查四边形的应用,解题的关键是理解新定义,并熟练运用勾股定理.
45.
【分析】
连接交于点,则可证得,,可证四边形为平行四边形,且,可证得四边形为菱形;根据勾股定理计算的长,可得结论.
【详解】
如图,连接交于点,
∵四边形为正方形,
∴,,
∵,
∴,即,
∴四边形为平行四边形,且,
∴四边形为菱形,
∴,
∵,,
由勾股定理得:,
∴四边形的周长,
故答案为.
【点睛】
本题考查了正方形的性质、菱形的判定和性质及勾股定理,掌握对角线互相垂直平分的四边形为菱形是解题的关键.
46.2.5
【分析】
首先根据折叠的性质与矩形的性质,得到AF=AB=5,EF=BE,AD=BC=4;然后在Rt△ADF中,利用勾股定理,求得DF的长,进而得到CF的长;再设CE=x,则EF=BE=4-x,在Rt△CEF中,利用勾股定理列出关于x的方程,求得x的值,最后由BE=BC-CE,即可得到结果.
【详解】
解:由题意可得AF=AB=5,AD=BC=4,EF=BE,
在Rt△ADF中,由勾股定理,得DF===3.
在矩形ABCD中,DC=AB=5,
∴CF=DC-DF=2.
设CE=x,则EF=BE=4-x,
在Rt△CEF中,CE2+CF2=EF2,即x2+22=(4-x)2,
解得x=1.5,
则BE=4-x=2.5.
故答案为2.5.
点睛:本题考查翻折变换、矩形的性质,找出线段间的关系,利用勾股定理列出等量关系式是解题的关键.
47.AD=DC(答案不唯一)
【详解】
试题分析:由四边形ABCD是平行四边形,
添加AD=DC,根据邻边相等的平行四边形是菱形的判定,可使得平行四边形ABCD为菱形;
添加AC⊥BD,根据对角线互相垂直的平行四边形是菱形的判定,可使得平行四边形ABCD为菱形.
答案不唯一.
48.5.
【分析】
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【详解】
解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为5
【点睛】
本题考查轴对称-最短路线问题;菱形的性质.
49.
【详解】
如图,连接AO交EF于点P,
由菱形和折叠对称的性质,知四边形AEOF是菱形,且AP=OP.
∵点A恰好落在菱形的对称中心O处,∴AE=BE.
∵AB=2,∠A=120°,
∴Rt△AEF中,AE=1,∠AEP=30°.
∴EP=.
∴EF=.
50.()n﹣1
【详解】
解:∵四边形ABCD为正方形,
∴AB=BC=1,∠B=90°,∴AC=;
同理可求:AE=,HE=,…,
∴第n个正方形的边长an=.
故答案为.
51.16
【详解】
试题分析:先利用三角形中位线性质得到AB=4,然后根据菱形的性质计算菱形ABCD的周长.
∵E,F分别是AD,BD的中点, ∴EF为△ABD的中位线, ∴AB=2EF=4,
∵四边形ABCD为菱形, ∴AB=BC=CD=DA=4, ∴菱形ABCD的周长=4×4=16.
考点:(1)菱形的性质;(2)三角形中位线定理.
52.24
【详解】
已知对角线的长度,根据菱形的面积计算公式即可计算菱形的面积.
解:根据对角线的长可以求得菱形的面积,
根据S=ab=×6×8=24cm2,
故答案为24.
53.4
【详解】
分析:由□ABCD的周长为26cm,对角线AC、BD相交于点O,若△AOD的周长比△AOB的周长多3cm,可得AB+AD=13cm,AD-AB=3cm,求出AB和AD的长,得出BC的长,再由直角三角形斜边上的中线性质即可求得答案.
详解:∵□ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OD+AD)-(OA+OB+AB)=AD-AB=3cm,
∴AB=5cm,AD=8cm.
∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4cm;
故答案为4.
点睛: 此题考查了平行四边形的性质、直角三角形斜边上的中线性质.熟练掌握平行四边形的性质,由直角三角形斜边上的中线性质求出AE是解决问题的关键.
54.(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3).
【详解】
试题分析:(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论(3)根据等腰直角三角形的性质得到BC=AB=4,AH=BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
试题解析:解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
(2)成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD;
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=AB=4,AH=BC=2,
∴CD=BC=1,CH=BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG==.
考点:四边形综合题.
55.(1)见解析;(2)6
【分析】
(1)根据DB⊥BC,CF⊥AE,得出∠D=∠AEC,再结合∠DBC=∠ECA=90°,且BC=CA,证明△DBC≌△ECA,即可得证;
(2) 由(1)可得△DBC≌△ECA,可得CE=BD,根据BC=AC=12cm AE是BC的中线,即可得出,即可得出答案.
【详解】
证明:(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,且BC=CA,
在△DBC和△ECA中,
∴△DBC≌△ECA(AAS).
∴AE=CD;
(2) 由(1)可得△DBC≌△ECA
∴CE=BD,
∵BC=AC=12cm AE是BC的中线,
∴,
∴BD=6cm.
【点睛】
本题考查了全等三角形的判定和性质,直角三角形斜边上的中线,证明△DBC≌△ECA解题关键.
56.(1)证明见解析;(2)成立,证明见解析.
【详解】
解:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA,
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE
∴∠MEA=∠AFO,
∴Rt△BOE≌ Rt△AOF
∴OE=OF
(2)OE=OF成立
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA
又∵AM⊥BE,
∴∠F+∠MBF=90°=∠E+∠OBE
又∵∠MBF=∠OBE
∴∠F=∠E
∴Rt△BOE≌Rt△AOF
∴OE=OF
57.(1)PB=PQ.证明见解析;(2)PB=PQ.证明见解析.
【详解】
试题分析:(1)过P作PE⊥BC,PF⊥CD,证明Rt△PQF≌Rt△PBE,即可;
(2)证明思路同(1).
试题解析:(1)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
考点: 正方形的判定与性质;全等三角形的判定与性质.
58.60°
【详解】
试题分析:根据正方形和等边三角形的性质可得:∠BAD=90°,∠DAE=60°,根据△BAE为等腰三角形可得:∠ABE=∠AEB=15°,根据正方形的性质可得:∠BCF=45°,∠CBF=90°-15°=75°,根据△BCF的内角和定理可得:∠BFC=180°-45°-75°=60°.
考点:(1)、等腰三角形的性质;(2)、三角形内角和定理;(3)、等边三角形的性质
59.(1)见解析;(2)120°;;(3)见解析
【分析】
(1)证明∠BAC=∠DAE,得出∠BAD=∠CAE,由SAS即可得出结论;
(2)求出∠ACB=∠ACE=30°,由平行线的性质得出∠MEC+∠ECD=180°,即可得出结果;
(3)由△BAD≌△CAE,得出DB=CE,再证明∠ACE=∠EMC,得出ME=EC,推出DB=ME,即可得出结论.
【详解】
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠BAC=180°-2∠ABC,
∵以AD、AE为腰做等腰三角形ADE,
∴AD=AE,
∴∠ADE=∠AED,
∴∠DAE=180°-2∠ADE,
∵∠ADE=∠ABC,
∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS);
(2)解:∵AB=AC,
∴∠ACB=∠ABC=30°,
∵△BAD≌△CAE,
∴∠ABD=∠ACE=30°,
∴∠ACB=∠ACE=30°,
∴∠ECB=∠ACB+∠ACE=60°,
∵EM∥BC,
∴∠MEC+∠ECD=180°,
∴∠MEC=180°﹣60°=120°;
(3)证明:∵△BAD≌△CAE,
∴DB=CE,∠ABD=∠ACE,
∵AB=AC,
∴∠ABD=∠ACB,
∴∠ACB=∠ACE,
∵EM∥BC,
∴∠EMC=∠ACB,
∴∠ACE=∠EMC,
∴ME=EC,
∴DB=ME,
又∵EM∥BD,
∴四边形MBDE是平行四边形.
【点睛】
本题考查了平行四边形的判定、等腰三角形的判定与性质、平行线的性质、全等三角形的判定与性质等知识;熟练掌握全等三角形的判定与性质是解题的关键.
60.(1)相等,垂直;(2)成立,见解析;(3)2.
【分析】
(1)利用SAS证明△ABE≌△CBF,延长CF交AB于点M,证明∠AMC=90°即可;
(2)仿照(1)的证明方法求解即可;
(3)根据题意,得点F在以B为圆心,BF为半径的圆上运动,根据直径最大原理,知道当C,B,F三点一线时,CF最大,此时点E恰好在AB的延长线上,连接DE,利用勾股定理求值即可.
【详解】
(1)如图①,∵正方形ABCD和等腰直角△BEF,
∴BA=BC,∠EBA=∠FBC=90° ,BE=BF,
∴△ABE≌△CBF,
∴AE=CF,
延长CF交AE于点M,
∵△ABE≌△CBF,
∴∠EAB=∠FCB ,
∵∠AFM=∠BFC ,
∴∠AMF=∠FBC=90° ,
∴AE⊥CF,
故答案为:相等,垂直;
(2)结论还成立.理由如下:
如图②,∵正方形ABCD和等腰直角△BEF,
∴BA=BC,∠EBF=∠ABC=90° ,BE=BF,
∴∠EBF-∠ABF =∠ABC-∠ABF,
∴∠EBA =∠FBC,
∴△ABE≌△CBF,
∴AE=CF,
延长CF交AE于点N,交AB于点G,
∵△ABE≌△CBF,
∴∠EAB=∠FCB ,
∵∠AGN=∠BGC ,
∴∠ANG=∠GBC=90° ,
∴AE⊥CF,
故结论成立;
(3)如图③,根据题意,得点F在以B为圆心,BF为半径的圆上运动,根据直径最大原理,知道当C,B,F三点一线时,CF最大,此时点E恰好在AB的延长线上,连接DE,∵AB= 2BF = 4,
∴AE=AB+BE=6,
在直角三角形ADE中,
DE==2.
【点睛】
本题考查了正方形的性质,等腰直角三角形的性质,三角形的全等,勾股定理,直径是圆中的最大的弦,垂直的定义,熟练掌握三角形全等,垂直的证明是解题的关键.
61.(1)见解析
(2)45°,理由见解析
【分析】
(1)根据平行线的性质可得∠ADO=∠ECO,再根据中点定义可得DO=CO,然后可利用ASA证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,由(1)得四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
【详解】
解:(1)∵四边形ABCD是平行四边形
∴AD∥BE
∴∠ADO=∠ECO
又∵O是CD的中点
∴OD=OC
在△AOD和△EOC中
∴△AOD ≌ △EOC (ASA)
(2)45°
由(1)知,OA=OE,OC=OD
∴四边形ACED是平行四边形
∴AD=CE
又∵四边形ABCD是平行四边形
∴AD=BC
∴BC =CE
当∠B=∠AEB=45°时,
且
∴四边形ACED是正方形.
【点睛】
本题考查了全等三角形的判定与性质,以及正方形的判定,关键是掌握对角线互相垂直且相等的平行四边形是正方形.
62.(1)证明见解析;(2)
【详解】
(1)如图1中,结论:△BCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠CBE=∠AEB,
∵EB平分∠AEC,
∴∠AEB=∠BEC,
∴∠CBE=∠BEC,
∴CB=CE,
∴△CBE是等腰三角形;
(2)如图2中,∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠D=90°,BC=AD=5,
在Rt△ECD中,∵∠D=90°,ED=AD-AE=4,EC=BC=5,
在中,∵∠A=90°,AB=3.AE=1,
63.(1)见详解;(2)
【分析】
(1)先证明AB∥CE,再推出∠ADB=∠OBC=60°,从而得AD∥BC,进而得到结论;
(2)根据勾股定理求出AO的长,再根据平行四边形的面积公式,即可求解.
【详解】
(1)证明:∵∠OAB=90°,
∴AB⊥x轴,
∵y轴⊥x轴,
∴AB∥y轴,即AB∥CE,
∵∠AOB=30°,
∴∠OBA=60°,
∵∠OAB=90°,D是OB的中点,
∴DB=DO= =4,
∵∠AOB=30°,
∴AB= =4,
∵DB=DO=AB =4,
∴∠BDA=∠BAD=(180°-60°)÷2=60°,
∵△OBC是等边三角形,
∴∠OBC=60°,
∴∠ADB=∠OBC,
即AD∥BC,
∴四边形ABCE是平行四边形;
(2)在直角△OAB中,AB=4,BO=8,
∴AO=,
∴平行四边形ABCE的面积=AB AO=.
【点睛】
本题主要考查直角三角形的性质,等边三角形的性质,勾股定理以及平行四边形的判定定理,熟练掌握平行四边形的判定定理是解题的关键.
64.(1)见解析;(2)
【分析】
(1)证明四边形CFBD是平行四边形,再证明∠1=90°,即可判定四边形CFBD是菱形.
(2)根据菱形的性质求得EF=1,再由勾股定理求得CE=3,由三角形的中位线定理可得AC=2,再由勾股定理即可求得.
【详解】
(1)证明:∵E是边BC的中点,
∴BE=EC,
∵ DE=EF,BE=EC,
∴四边形CFBD是平行四边形,
∵D是AB边中点,E是BC中点,
∴DE∥AC,
∴∠1=∠ACB=90°,
∴四边形CFBD是菱形.
(2)∵四边形CFBD是菱形,
∴∠CEF=90°.
∵DF=2,
∴EF=1,
∵,
∴由勾股定理得,CE=3,
∵D,E分别是边AB,BC的中点,DE=1,
∴AC=2,
∵∠ACB=90°,
由勾股定理得.
【点睛】
本题考查了菱形的判定与性质、勾股定理等知识,熟练运用相关知识是解决问题的关键.
65.(1)证明见解析;(2)四边形DEBF是平行四边形,理由见解析.
【详解】
分析:(1)利用平行四边形ABCD的对角相等,对边相等的性质推知∠A=∠C,AD=BC;然后根据全等三角形的判定定理AAS证得结论;
(2)由“对边平行且相等的四边形是平行四边形”推知四边形DEBF是平行四边形.
详解:(1)证明:∵四边形ABCD为平行四边形,
∴∠A=∠C,AD=BC,
在△ADE与△CBF中,
∴△ADE≌△CBF(ASA);
(2)四边形DEBF是平行四边形.理由如下:
∵DF∥EB,又由△ADE≌△CBF,知AE=CF,
∴AB﹣AE=CD﹣CF,即DF=EB.
∴四边形DEBF是平行四边形
点睛:本题考查了全等三角形的判定与性质、平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
66.(1)见解析;(2)能,;(3)或,理由见解析
【分析】
(1)由已知条件可得Rt△CDF中∠C=30°,即可知DF=CD=AE=2t;
(2)由DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;
(3)分∠EDF=90°、∠DEF=90°两种情况,根据直角三角形的性质列出算式,计算即可.
【详解】
(1)证明:∵在中,,
,,
∴.
∵,,
在直角中,,
∴,
∴;
(2)∵,,
∴四边形是平行四边形,
当时,四边形是菱形,
即,
解得:,
即当时,平行四边形是菱形;
(3)当时是直角三角形();
当时,是直角三角形().
理由如下:
当时,
∴
∴
∵,
∴,
∴,
∴,
∴时,.
当时,,
∵四边形是平行四边形,
∴,
∴,
∴是直角三角形,,
∵,
∴,
∴,,
,
∴,
解得.
综上所述,当时是直角三角形();当时,是直角三角形().
【点睛】
本题是四边形综合题,考查了直角三角形的性质、平行四边形的判定与性质、菱形的性质、含角的直角三角形的性质等知识点,熟练掌握平行四边形、菱形的判定是解题的关键.
67.(1)5;(2)见解析
【分析】
(1)依据,,可得是等腰直角三角形,结合求出,再根据勾股定理,即可求解的长;
(2)连接GE,过A作,交BG于P,连接PE,利用正方形的判定方法可证得四边形是正方形,即可得到,,进而得出,依据,,即可得到.
【详解】
(1)解:∵,,
∴,
∴,
∴是等腰直角三角形,
∴.
∵,
∴,
∵,
∴.
(2)如图,连接GE,过A作,交BG于P,连接PE,
∵,,
∴,
∴BG是AE的垂直平分线,
∴,
∵,
∴是等腰直角三角形,即,
是等腰直角三角形,即,
∴,
∵,
∴四边形是正方形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
又∵,
∴.
【点睛】
本题考查了平行四边形的性质、正方形的判定与性质以及全等三角形的判定与性质等知识,掌握特殊四边形的判定与性质并能灵活运用所学知识是解题的关键.
68.(1)见解析;(2)见解析;(3),理由见解析.
【分析】
(1)根据题意按步骤画图即可;
(2)根据平行线的性质和角平分线的定义得出,则,进而有,然后利用一组对边平行且相等的四边形是平行四边形即可证明;
(3)根据菱形的性质有,然后利用等腰三角形的性质和平行线的性质即可求解.
【详解】
(1)补全图形如下:
(2) ,
.
,
.
∵AD平分,
,
,
,
.
,
∴四边形BEFG是平行四边形;
(3),理由如下:
若四边形BEFG是菱形,则有,
,
,
.
∵四边形BEFG是平行四边形,
,
.
【点睛】
本题主要考查平行四边形的判定及性质,菱形的性质,掌握平行四边形的判定及性质和菱形的性质是解题的关键.
答案第1页,共2页
一、单选题
1.(2021·黑龙江龙凤·八年级期末)如图,在平行四边形ABCD中,下列各式不一定正确的是( )
A. B.
C. D.
2.(2021·黑龙江碾子山·八年级期末)如图,在平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
3.(2021·黑龙江萝北·八年级期末)如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.3和2 B.2和3 C.4和1 D.1和4
4.(2021·黑龙江绥滨·八年级期末)如图,在中,平分,则的长是( )
A. B.
C. D.
5.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)在平行四边形ABCD中,若∠A∶∠B=5∶4,则∠C的度数为( )
A.80° B.120° C.100° D.110°
6.(2021·黑龙江南岗·八年级期末)若中,,则的度数为( ).A. B. C. D.
7.(2021·黑龙江巴彦·八年级期末)如的对角线与相较于,,若,,则长( )
A.6 B.10 C.12 D.18
8.(2021·黑龙江勃利·八年级期末)如图,平行四边形ABCD中,AD=5,AB=3,BE 平分∠ABC交AD边于点E,则线段AE、ED的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
9.(2021·黑龙江林口·八年级期末)下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠C,∠B=∠D
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
10.(2021·黑龙江龙凤·八年级期末)下列说法中,不正确是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行另一组对边相等的四边形是平行四边形
11.(2021·黑龙江林口·八年级期末)已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A. B. C.2 D.
12.(2021·黑龙江龙凤·八年级期末)如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长为( )
A. B. C.3 D.4
13.(2021·黑龙江木兰·八年级期末)如图所示,在中,,,分别是,,的中点,,,则四边形的周长是( )
A.10 B.20 C.30 D.40
14.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)如图,E,F是四边形ABCD两边AB,CD的中点,G,H是对角线AC,BD的中点,若EH=6,则以下结论不正确的是( )
A. B. C. D.
15.(2021·黑龙江克山·八年级期末)如图,过 ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG的面积S1与 HCFM的面积S2的大小关系是( )
A.S1=S2 B.S1>S2 C.S1
A.3cm B.26cm C.24cm D.65cm
17.(2021·黑龙江爱辉·八年级期末)如图,已知 OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A.3 B.4 C.5 D.6
18.(2021·黑龙江龙凤·八年级期末)如图,在平行四边形ABCD中,过对角线BD上一点P,作EF∥BC,HG∥AB,若四边形AEPH和四边形CFPG的面积分另为S1和S2,则S1与S2的大小关系为( )
A.S1=S2 B.S1>S2 C.S1<S2 D.不能确定
19.(2021·黑龙江道里·八年级期末)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A. B.6 C.4 D.5
20.(2021·黑龙江道外·八年级期末)如图,在矩形纸片ABCD中,AB=6,AD=8,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则线段EF的长为( )
A.3 B.4 C.5 D.6
21.(2021·黑龙江绥棱·八年级期末)如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF,其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
22.(2021·黑龙江克山·八年级期末)如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A.30° B.45° C.60° D.75°
23.(2021·黑龙江林口·八年级期末)如图,将一张矩形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是( )
A.112° B.136° C.144° D.158°
24.(2021·黑龙江勃利·八年级期末)如图,矩形中,,,在数轴上,若以点A为圆心,对角线的长为半径作弧交数轴于点M,则点M表示的数为( )
A.2 B. C. D.
25.(2021·黑龙江铁锋·八年级期末)如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
A.下滑时,OP增大 B.上升时,OP减小
C.无论怎样滑动,OP不变 D.只要滑动,OP就变化
26.(2021·黑龙江铁锋·八年级期末)在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
27.(2021·黑龙江集贤·八年级期末)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
A.20° B.25° C.30° D.40°
28.(2021·黑龙江讷河·八年级期末)如图,在菱形中,P是对角线上一动点,过点P作于点E.于点F.若菱形的周长为20,面积为24,则的值为( )
A.4 B. C.6 D.
29.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)矩形具有而菱形不具有的性质是【 】
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
30.(2021·黑龙江绥棱·八年级期末)已知四边形是平行四边形,下列结论中不正确的是( )
A.当时,它是菱形 B.当时,它是正方形
C.当时,它是矩形 D.当时,它是菱形
31.(2021·黑龙江昂昂溪·八年级期末)如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法判断
32.(2021·黑龙江昂昂溪·八年级期末)如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是( )
A.3 B.2 C.3 D.6
33.(2021·黑龙江绥滨·八年级期末)如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①②③
34.(2021·黑龙江·齐齐哈尔市富拉尔基区教师进修学校八年级期末)如图,在中,点E为边DC上一点,连接AE,将沿AE翻折,点D的对应点落在边AB上,,,则边BC的长是( )
A.5 B.6 C.7 D.8
35.(2021·黑龙江木兰·八年级期末)如图.正方形和正方形中,点在上,,,是的中点,那么的长是( ).
A. B. C. D.2
36.(2021·黑龙江爱辉·八年级期末)正方形具有而菱形不一定具有的性质是( )
A.四条边都相等 B.对角线互相垂直且平分
C.对角线相等 D.对角线平分一组对角
37.(2021·黑龙江道里·八年级期末)下列命题错误的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.对角线互相垂直的矩形是正方形
38.(2021·黑龙江牡丹江·八年级期末)如图,四边形是正方形,线段交于点,连接,,点在线段上,,于.下列结论:①;②;③平分;④;⑤若,则,其中正确结论的个数是( )
A. B. C. D.
39.(2021·黑龙江铁锋·八年级期末)如图,已知在正方形ABCD中,厘米,,点E在边AB上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动时间为t秒.若存在a与t的值,使与全等时,则t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
40.(2021·黑龙江南岗·八年级期末)下列命题中,假命题的是( )
A.四个角都相等的四边形是矩形
B.对角线互相平分且垂直的四边形是菱形
C.对角线互相垂直且相等的四边形是正方形
D.对角线相等的平行四边形是矩形
41.(2021·黑龙江昂昂溪·八年级期末)如图,正方形的面积为,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( ).
A. B. C. D.
二、填空题
42.(2021·黑龙江龙凤·八年级期末)如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
43.(2021·黑龙江集贤·八年级期末)如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________(只添一个即可),使四边形ABCD是平行四边形.
44.(2021·黑龙江林口·八年级期末)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线交于点.若,则__________.
45.(2021·黑龙江南岗·八年级期末)如图,,是正方形的对角线上的两点,,,则四边形的周长是_____.
46.(2021·黑龙江集贤·八年级期末)矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为_____________.
47.(2021·黑龙江讷河·八年级期末)如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件:___,使得平行四边形ABCD为菱形.
48.(2021·黑龙江绥棱·八年级期末)已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=___.
49.(2021·黑龙江绥滨·八年级期末)如图,将菱形纸片ABCD折迭,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2 cm,∠A=120°,则EF=_______cm.
50.(2021·黑龙江绥滨·八年级期末)如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为_____.
51.(2021·黑龙江·肇州县教师进修学校八年级期末)如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是__.
52.(2021·黑龙江南岗·八年级期末)若菱形的两条对角线长分别是6㎝和8㎝,则该菱形的面积是____㎝2.
53.(2021·黑龙江绥棱·八年级期末)如图, ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为______cm.
三、解答题
54.(2021·黑龙江林口·八年级期末)△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF,
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB=2,CD=BC,请求出GE的长.
55.(2021·黑龙江昂昂溪·八年级期末)如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D.
求证:(1)AE=CD.(2)若AC=12cm,求BD的长.
56.(2021·黑龙江绥滨·八年级期末)如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AMBE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AMBE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗.如果成立,请给出证明;如果不成立,请说明理由.
57.(2021·黑龙江绥棱·八年级期末)如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
58.(2021·黑龙江·五常市教师进修学校八年级期末)如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为__________°.
59.(2021·黑龙江龙凤·八年级期末)已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.
(1)求证:△BAD≌△CAE;
(2)若∠ABC=30°,求∠MEC的度数;
(3)求证:四边形MBDE是平行四边形.
60.(2021·黑龙江昂昂溪·八年级期末)综合与实践
(1)问题发现:正方形ABCD和等腰直角△BEF按如图①所示的方式放置,点F在AB上,连接AE、CF,则AE、CF的数量关系为 ,位置关系为 .
(2)类比探究:正方形ABCD保持固定,等腰直角△BEF绕点B顺时针旋转,旋转角为α(0°<α ≤360°),请问(1)中的结论还成立吗?请就图②说明你的理由:
(3)拓展延伸:在(2)的条件下,若AB= 2 BF= 4,在等腰直角△BEF旋转的过程中,当CF为最大值时,请直接写出DE的长.
61.(2021·黑龙江绥棱·八年级期末)已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:;
(2)连接AC,DE,当 四边形ACED是正方形?请说明理由.
62.(2021·黑龙江·五常市教师进修学校八年级期末)在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC,
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
63.(2021·黑龙江龙凤·八年级期末)如图,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形.
(2)求四边形ABCE的面积.
64.(2021·黑龙江铁锋·八年级期末)如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.
(1)求证:四边形CFBD是菱形;
(2)连接AE,若CF=,DF=2,求AE的长.
65.(2021·黑龙江萝北·八年级期末)如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.
(1)求证:△ADE≌△CBF;
(2)判定四边形DEBF是否是平行四边形?
66.(2021·黑龙江集贤·八年级期末)如图,在中,,,,点从点出发沿方向以4cm/s的是速度向点匀速运动,同时点从出发沿方向以2cm/s的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点、运动的时间是s.过点作于点,连接、.
(1)求证:;
(2)四边形能够成为菱形吗?如果能,求出相应的值;如果不能,请说明理由;
(3)当为何值时,为直角三角形?请说明理由.
67.(2021·黑龙江木兰·八年级期末)如图,在中,,点在对角线上,,于点,的延长线交于点.点在的延长线上,且,连接.
(1)若,,求的长;
(2)求证:.
68.(2021·黑龙江牡丹江·八年级期末)如图,已知等腰,,平分,为上一动点,作平行,交于F,在上取一点,使得,连接.
(1)根据题意补全图形;
(2)求证四边形是平行四边形;
(3)若,写出一个的度数,使得四边形是菱形.
试卷第1页,共3页
参考答案:
1.D
【详解】
由 ABCD的性质及图形可知:
A、∠1和∠2是邻补角,故∠1+∠2=180°,正确;
B、因为AD∥BC,所以∠2+∠3=180°,正确;
C、因为AB∥CD,所以∠3+∠4=180°,正确;
D、根据平行四边形的对角相等,∠2=∠4,∠2+∠4=180°不一定正确;
故选D.
2.B
【分析】
由AC的垂直平分线交AD于E,易证得AE=CE,又由四边形ABCD是平行四边形,即可求得AD与DC的长,继而求得答案.
【详解】
解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,
∴△CDE的周长是:DC+DE+CE=DC+DE+AE=DC+AD=3+5=8,
故选B.
【点睛】
此题考查线段垂直平分线的性质,平行四边形的性质,解题关键在于得到AE=CE.
3.A
【分析】
利用平行四边形的性质、角平分线的性质和等腰三角形的性质可得AD=BC,BE= AB,然后根据EC=BC-BE即可.
【详解】
解:∵AE平分∠BAD
∴∠BAE=∠DAE
∵四边形ABCD是平行四边形
∴AD//BC,AD=BC
∴∠DAE=∠AEB
∴∠BAE=∠BEA
∴AB=BE=3
∴EC=AD-BE=2
故答案为A.
【点睛】
本题主要考查了平行四边形性质及等腰三角形的性质,根据题意说明△ABE是解答本题的关键.
4.C
【分析】
根据平行四边形的性质得出AB=CD,AD=BC=6,AD∥BC,根据平行线性质求出∠ADE=∠DEC,根据角平分线定义求出∠ADE=∠CDE,推出∠CDE=∠DEC,推出CE=DC,求出CD即可.
【详解】
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=6,AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴CE=DC,
∵BC=6,BE=2,
∴CD=CE=6-2=4,
故选:C.
【点睛】
本题考查了平行四边形的性质,角平分线定义,平行线的性质,等腰三角形的性质和判定的应用,解题的关键是求出CD的长,注意:平行四边形的对边平行且相等,难度适中.
5.C
【分析】
根据平行四边形的性质可知∠A,∠B互补,再根据已知可以求出∠A,∠B的度数,而∠C是∠A的对角,所以相等即可得出答案.
【详解】
解:∵四边形ABCD是平行四边形
∴AD//BC,∠A=∠C
∴∠A+∠B=180°,
∵∠A:∠B=5:4
∴∠A=100°,∠B=80°
∴∠C=∠A=100°.
故选:C.
【点睛】
本题主要考查了平行四边形的性质;①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.
6.A
【分析】
根据平行四边形对角相等即可求解.
【详解】
解:∵平行四边形ABCD中,∠A=38°,
∴∠C=∠A=38°,
故选A.
【点睛】
本题考查了平行四边形的应用,熟练掌握平行四边形对角相等的性质是解题关键.
7.C
【分析】
利用平行四边形的性质和勾股定理易求AO的长,进而可求出AC的长.
【详解】
解:∵ ABCD的对角线AC与BD相交于点O,
∴,,
∵AB⊥AC,
∴∠BAO=90°,
∴,
∴AC=2AO=12,
故选C.
【点睛】
本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.
8.B
【分析】
根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得DE的长度.
【详解】
解:∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC=5,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3,
∴DE=AD﹣AE=5﹣3=2
故选B.
【点睛】
本题主要考查了平行四边形的性质,角平分线的性质,解题的关键在于能够熟练掌握相关性质进行求解.
9.A
【分析】
直接根据平行四边形的判定定理判断即可.
【详解】
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断;
平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴B能判断;
平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴D能判定;
平行四边形判定定理3,对角线互相平分的四边形是平行四边形;
平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;
故选A.
【点睛】
此题是平行四边形的判定,解本题的关键是掌握和灵活运用平行四边形的5个判断方法.
10.D
【分析】
由平行四边形的判定方法得出A、B、C正确;即可得出结论.
【详解】
解:∵对角线互相平分的四边形是平行四边形,
∴A正确;
∵两组对角分别相等的四边形是平行四边形,
∴B正确;
∵一组对边且相等的四边形是平行四边形,
∴C正确;
∵一组对边平行另一组对边相等的四边形是等腰梯形,不一定是平行四边形,
∴D不正确.
故选D.
【点睛】
本题考查了平行四边形的判定方法:熟练掌握平行四边形的判定方法,并能进行推理论证是解决问题的关键.
11.D
【分析】
由AE平分∠BAD得∠BAE=∠DAE,根据矩形ABCD可得△ABE是等腰直角三角形,所以BE=AB=3,从而可求EC=1,连接DE,由勾股定理得DE的长,再根据三角形中位线定理可求FG的长.
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE=3,
∵BC=AD=4,
∴EC=1,
连接DE,如图,
∴DE=,
∵点F、G分别为AD、AE的中点,
∴FG=.
故选D.
【点睛】
本题考查了矩形的性质以及三角形中位线定理,熟记性质与定理是解题关键.
12.C
【详解】
首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为26,及BC=10,可得DE=6,利用中位线定理可求出PQ.
13.A
【分析】
根据三角形的中位线平行于第三边,并且等于第三边的一半,以及中点的定义可得,,再根据四边形的周长的定义计算即可得解
【详解】
解:在中,、、分别是、、的中点,
,,
四边形的周长是.
故选:.
【点睛】
本题考查了三角形中位线定理,中点的定义以及四边形周长的定义,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.
14.D
【分析】
由三角形中位线定理可得EH∥AD,EH=AD,GF∥AD,GF=AD,可得EH∥GF,EH=GF=6,AD=2EH=12,利用排除法可求解.
【详解】
解:∵E、F是AB、CD的中点,G、H是AC、BD的中点,
∴EH∥AD,EH=AD,GF∥AD,GF=AD,
∴EH∥GF,EH=GF=6,
∴AD=2EH=12,
故选:D.
【点睛】
本题考查了三角形中位线定理,掌握三角形的中位线定理是本题的关键.
15.A
【分析】
根据平行四边形的性质和判定得出平行四边形GBEP、GPFD,证△ABD≌△CDB,得出△ABD和△CDB的面积相等;同理得出△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,相减即可求出答案.
【详解】
∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
∵
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故选A.
【点睛】
本题考查了平行四边形的性质和判定,全等三角形的性质和判定的应用,解此题的关键是求出△ABD和△CDB的面积相等,△BEP和△PGB的面积相等,△HPD和△FDP的面积相等,注意:如果两三角形全等,那么这两个三角形的面积相等
16.B
【详解】
如图所示:
∵D,E,F分别是△ABC的三边的中点,
∴DE= AC,DF=BC,EF=AB,
∴AC+BC+AB=2(DE+DF+EF)=2×(3+4+6)=26(cm).
故选B.
17.C
【分析】
过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E.则OB=.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.
【详解】
解:过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,
,
∴△OAF≌△BCD.
∴BD=OF=1,
∴OE=4+1=5,
∴OB=.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=5.
故选:C.
【点睛】
本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
18.A
【详解】
试题分析:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形GBEP、HPFD是平行四边形,
∵在△ABD和△CDB中,AB=CD,BD=BD,AD=BC,
∴△ABD≌△CDB,
即△ABD和△CDB的面积相等;
同理△BEP和△PGB的面积相等,△HPD和△FDP的面积相等,
∴四边形AEPH和四边形CFPG的面积相等,即S1=S2.
故选A.
考点:1.平行四边形的判定与性质2.全等三角形的判定与性质.
19.B
【详解】
∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,
∴AF=AB,∠AFE=∠B=90°,
∴EF⊥AC,
∵∠EAC=∠ECA,
∴AE=CE,
∴AF=CF,
∴AC=2AB=6,
故选B.
【点睛】本题考查了翻折变换的性质、矩形的性质等,得到EF垂直平分AC是解题的关键.
20.A
【分析】
根据矩形的性质可得BC=AD,∠B=90°,利用勾股定理可求出AC的长,根据折叠的性质可得AF=AB,∠B=∠AFE=90°,BE=EF,在Rt△CEF中利用勾股定理列方程求出EF的长即可得答案.
【详解】
∵四边形ABCD是矩形,AD=8,
∴∠B=90°,BC=AD=8,
∴AC==10,
∵折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,
∴BE=EF,AF=AB=6,∠AFE=∠B=90°,
∴CF=AC-AF=10﹣6=4,
在Rt△CEF中,由勾股定理得,EF2+CF2=CE2,
∴EF2+CF2=(BC-EF)2,即EF2+42=(8-EF)2,
解得:EF=3,
故选:A.
【点睛】
本题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.
21.B
【详解】
试题分析:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF.
由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC.
∵BF平分∠EBC,∴CF=MF.∴DF=CF.故①正确.
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC.
∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN.
∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN.故②正确.
∵在△DEF和△CNF中,易由ASA得△DEF≌△CNF,∴EF=FN.∴BE=BN.
但无法求得△BEN各角的度数,
∴△BEN不一定是等边三角形.故③错误.
∵∠BEM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM.∴BM=3EM.
∴S△BEF=3S△EMF=3S△DEF.故④正确.
综上所述,正确的结论是①②④.故选B.
22.C
【详解】
如图所示:
由题意可得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=AM,故AN=NG,
则∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=×90°=30°,
∴∠DAG=60°.
故选C.
23.B
【分析】
由AD//BC,∠EFG=68°,根据两直线平行,内错角相等,可求得∠DEF的度数,然后由折叠的性质,求得∠DEG的度数,继而求得答案.
【详解】
解:∵AD//BC,∠EFG=68°,
∴∠DEF=∠EFG=68°,
由折叠的性质可得:∠FEG=∠DEF=68°,
∴∠DEG=∠DEF+∠FEG=136°,
∵AD//BC,
∴∠1=∠DEG=136°.
故选:B.
【点睛】
此题考查了平行线的性质以及折叠的性质.注意掌握折叠前后图形的对应关系是解此题的关键.
24.C
【分析】
首先根据勾股定理计算出AC的长,进而得到AM的长,再根据A点表示-1,可得M点表示的数.
【详解】
解:∵矩形中,,,
∴,,
∴,
∴,
∵A点表示-1,
∴M点表示的数为:
故选:C.
【点睛】
此题主要考查了勾股定理和数轴的应用,矩形的性质,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
25.C
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得OP=AB.
【详解】
解:∵AO⊥BO,点P是AB的中点,
∴OP=AB,
∴在滑动的过程中OP的长度不变.
故选:C.
【点睛】
本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.
26.C
【分析】
根据矩形的判定条件逐项进行分析判断即可;
【详解】
解:A、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项B符合题意;
C、∵AD∥BC,
∴∠A+∠B=∠C+∠D=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,AB=CD,故选项C不符合题意;
D、∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴AB⊥AD,AB⊥BC,AB的长为AD、BC间的距离,
又∵AB=CD,
∴CD⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形,
∴选项D不符合题意;
故选:C.
【点睛】
本题主要考查了矩形的判定,准确分析判断是解题的关键.
27.A
【分析】
先根据菱形的性质得OD=OB,AB∥CD,BD⊥AC,则利用DH⊥AB得到DH⊥CD,∠DHB=90°,所以OH为Rt△DHB的斜边DB上的中线,得到OH=OD=OB,利用等腰三角形的性质得∠1=∠DHO,然后利用等角的余角相等即可求出∠DHO的度数.
【详解】
解:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠1=∠DHO,
∵DH⊥CD,
∴∠1+∠2=90°,
∵BD⊥AC,
∴∠2+∠DCO=90°,
∴∠1=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=20°,
∴∠DHO=20°,
故选A.
【点睛】
本题考查菱形的性质,直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
28.B
【分析】
连接BP,通过菱形的周长为20,求出边长,菱形面积为24,求出SABC的面积,然后利用面积法,SABP+SCBP=SABC,即可求出的值.
【详解】
解:连接BP,
∵菱形ABCD的周长为20,
∴AB=BC=20÷4=5,
又∵菱形ABCD的面积为24,
∴SABC=24÷2=12,
又SABC= SABP+SCBP
∴SABP+SCBP=12,
∴ ,
∵AB=BC,
∴
∵AB=5,
∴PE+PF=12×=.
故选:B.
【点睛】
本题主要考查菱形的性质,解题关键在于添加辅助线,通过面积法得出等量关系,求出PF+PE的值.
29.B
【详解】
根据矩形与菱形的性质对各选项解析判断后利用排除法求解:
A.矩形与菱形的两组对边都分别平行,故本选项错误;
B.矩形的对角线相等,菱形的对角线不相等,故本选项正确;
C.矩形与菱形的对角线都互相平分,故本选项错误;
D.矩形与菱形的两组对角都分别相等,故本选项错误.
故选B.
30.B
【分析】
根据菱形、正方形、矩形的判定方法一一判断即可.
【详解】
解:A、正确.根据邻边相等的平行四边形是菱形;
B、错误.对角线相等的四边形是矩形,不一定是正方形.
C、正确.有一个角是直角的平行四边形是矩形.
D、正确.对角线垂直的平行四边形是菱形.
故选:B.
【点睛】
此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,属于基础题.
31.B
【分析】
作DF⊥BC,BE⊥CD,先证四边形ABCD是平行四边形.再证Rt△BEC≌Rt△DFC,得,BC=DC,所以,四边形ABCD是菱形.
【详解】
如图,作DF⊥BC,BE⊥CD,
由已知可得,AD∥BC,AB∥CD
∴四边形ABCD是平行四边形.
在Rt△BEC和Rt△DFC中
∴Rt△BEC≌Rt△DFC,
∴BC=DC
∴四边形ABCD是菱形.
故选B
【点睛】
本题考核知识点:菱形的判定.解题关键点:通过全等三角形证一组邻边相等.
32.C
【分析】
首先连接AC,交BD于点O,连接CM,则CM与BD交于点P,此时PA+PM的值最小,由在菱形ABCD中,AB=6,∠ABC=60°,易得△ACD是等边三角形,BD垂直平分AC,继而可得CM⊥AD,则可求得CM的值,继而求得PA+PM的最小值.
【详解】
解:连接AC,交BD于点O,连接CM,则CM与BD交于点P,此时PA+PM的值最小,
∵在菱形ABCD中,AB=6,∠ABC=60°,
∴∠ADC=∠ABC=60°,AD=CD=6,BD垂直平分AC,
∴△ACD是等边三角形,PA=PC,
∵M为AD中点,
∴DM=AD=3,CM⊥AD,
∴CM==3,
∴PA+PM=PC+PM=CM=3.
故选C.
【点睛】
此题考查了最短路径问题、等边三角形的判定与性质、勾股定理以及菱形的性质.注意准确找到点P的位置是解此题的关键.
33.A
【分析】
菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形.据此判断即可.
【详解】
解:① ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定 ABCD是菱形;故①正确;
② ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故②错误;
③ ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定 ABCD是菱形;故③正确;
D、 ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故④错误.
故选:A.
【点睛】
此题考查了菱形的判定与矩形的判定定理.此题难度不大,注意掌握菱形的判定定理是解此题的关键.
34.A
【分析】
通过证明四边形ADED'是菱形,可得AE⊥DD',AO=EO=4,DO=D'O=3,由勾股定理可求AD的长,即可求BC的长.
【详解】
如图,设AE与的交点为.
∵四边形ABCD是平行四边形,
∴,.
∵将沿AE翻折,
,,.
∵,
∴,
∴,
∴,
∴
∴四边形是菱形,
则,,,
∴,
∴.
故选:A.
【点睛】
本题考查了翻折变换,平行四边形的性质,菱形的判定和性质,勾股定理,证明四边形ADED'是菱形是本题的关键.
35.B
【分析】
连接AC、CF,如图,根据正方形的性质得∠ACD=45°,∠FCG=45°,AC=,CF=3,则∠ACF=90°,再利用勾股定理计算出AF=2,然后根据直角三角形斜边上的中线求CH的长.
【详解】
解:连接AC、CF,如图,
∵四边形ABCD和四边形CEFG都是正方形,
∴∠ACD=45°,∠FCG=45°,AC=BC=,CF=CE=3,
∴∠ACF=45°+45°=90°,
在Rt△ACF中,AF=,
∵H是AF的中点,
∴CH=AF=.
故选:B.
【点睛】
本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.两条对角线将正方形分成四个全等的等腰直角三角形.也考查了直角三角形斜边上的中线性质.
36.C
【分析】
根据正方形和菱形的性质逐项判断即可得.
【详解】
A、正方形和菱形的四条边都相等,则此项不符题意;
B、正方形和菱形的对角线都互相垂直且平分,则此项不符题意;
C、正方形的对角线相等,而菱形的对角线不一定相等,则此项符合题意;
D、正方形和菱形的对角线都平分一组对角,则此项不符题意;
故选:C.
【点睛】
本题考查了正方形和菱形的性质,熟练掌握正方形和菱形的性质是解题关键.
37.C
【详解】
解:A、对角线互相平分的四边形是平行四边形,正确,不符合题意;
B、对角线相等的平行四边形是矩形,正确,不符合题意;
C、一条对角线平分一组对角的四边形可能是菱形或者正方形,错误,符合题意;
D、对角线互相垂直的矩形是正方形,正确,不符合题意,
故选C.
【点睛】
本题考查命题与定理.
38.A
【分析】
①根据正方形的性质可得AD=AB,由AD=DE可求出AB=DE;过点D作DH⊥AE,根据等腰三角形的性质可得AH=,②再利用全等三角形的判定可得,由全等三角形的性质可得AH=BN,继而可得BN=;由∠AFD=45°可得∠FDH=45°,③∠FDE+∠EDH=45°,∠CDF+∠ADH=45°,从而可得∠CDF=∠FDE,继而求出DF平分∠CDE;④根据,即可得,根据,即可证明;⑤由条件可得为的角平分线,根据角平分线的性质,以及三角形的面积之比可得与的比,进而求解.
【详解】
解:①∵正方形ABCD,
∴AD=AB,
∵AD=DE,
∴AB=DE,故①正确;
②过点D作DH⊥AE,
∵AD=DE,
∴AH=,
∵∠DAH+∠BAE=90°,∠DAH+∠ADH=90°,
∴∠BAE=∠ADH,
在和中,
∵∠ANB=∠DHA=90°,∠BAN=∠ADH,AB=AD,
∴,
∴AH=BN,
∴BN=,故②正确;
③过点D作DH⊥AE,
∵AD=DE,
∴AH平分∠ADE,
∴∠EDH=∠ADH,
∵∠AFD=45°,∠DHF=90°,
∴∠FDH=45°,
∴∠FDE+∠EDH=45°,
又∵∠ADC=90°,
∴∠CDF+∠ADH=45°,
∴∠CDF=∠FDE,
∴DF平分∠CDE,故③正确;
④
,
即
故④正确
⑤若,
则
四边形是正方形
即为的角平分线
如图,过点作
.
故⑤正确.
故正确的有①②③④⑤,共5个
故选A
【点睛】
本题主要考查正方形的性质和全等三角形的判定与性质,等腰三角形的性质,角平分线性质,解决本题的关键是要熟练掌握正方形的性质和全等三角形的判定.
39.D
【分析】
根据题意分两种情况讨论若△BPE≌△CQP,则BP=CQ,BE=CP;若△BPE≌△CPQ,则BP=CP=5厘米,BE=CQ=6厘米进行求解即可.
【详解】
解:当,即点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∴BP=10-6=4厘米,
∴运动时间t=4÷2=2(秒);
当,即点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t=(秒).
综上t的值为2.5或2.
故选:D.
【点睛】
本题主要考查正方形的性质以及全等三角形的判定,解决问题的关键是掌握正方形的四条边都相等,四个角都是直角;两边及其夹角分别对应相等的两个三角形全等.同时要注意分类思想的运用.
40.C
【分析】
根据平行四边形,矩形,菱形和正方形的判定进行判断即可.
【详解】
解:A、四边形的内角和为360°,
∵四个角都相等,
∴四边形的每个角都等于90°,
∴此四边形是矩形,
故该命题是真命题;
B、对角线互相平分的四边形是平行四边形,
对角线垂直的平行四边形是菱形,
故该命题是真命题;
C、对角线互相平分、互相垂直且相等的四边形才是正方形,
故该命题是假命题;
D、对角线相等的平行四边形是矩形,是真命题.
故选C.
【点睛】
本题考查了从对角线来判断特殊四边形的方法:对角线互相平分的四边形为平行四边形;对角线互相垂直平分的四边形为菱形;对角线互相平分且相等的四边形为矩形;对角线互相垂直平分且相等的四边形为正方形.
41.C
【详解】
连接、、关于对称.
∴.
∴,当、、三点共线得最小.
∴,选.
点睛:本题考查的是正方的性质和轴对称-最短线题,熟知“两点之间,线段最短”是解答此的关键.
42.48
【分析】
首先根据平行四边形的性质可得AB=CD,AD=BC,可得AB+BC=20,再利用其面积的求法S=BC×AE=CD×AF,可得4AE=6CD,列出方程组,求出平行四边形的各边长,再求其面积.
【详解】
解:设BC=x,CD=y,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵ ABCD的周长为40,
∴x+y=20,
∵AE=4,AF=6,S=BC×AE=CD×AF,
∴4x=6y,
得方程组:,
解得:
∴S平行四边形ABCD=BC×AE=12×4=48.
故答案为:48.
【点睛】
此题主要考查了平行四边形的性质与其面积公式,解题的关键是根据性质得到邻边的和,根据面积公式得到方程,再解方程组即可.
43.BO=DO.
【详解】
解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
故答案为BO=DO.
44.20
【分析】
由垂美四边形的定义可得AC⊥BD,再利用勾股定理得到AD2+BC2=AB2+CD2,从而求解.
【详解】
∵四边形ABCD是垂美四边形,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2,
∵AD=2,BC=4,
∴AD2+BC2=22+42=20,
故答案为:20.
【点睛】
本题主要考查四边形的应用,解题的关键是理解新定义,并熟练运用勾股定理.
45.
【分析】
连接交于点,则可证得,,可证四边形为平行四边形,且,可证得四边形为菱形;根据勾股定理计算的长,可得结论.
【详解】
如图,连接交于点,
∵四边形为正方形,
∴,,
∵,
∴,即,
∴四边形为平行四边形,且,
∴四边形为菱形,
∴,
∵,,
由勾股定理得:,
∴四边形的周长,
故答案为.
【点睛】
本题考查了正方形的性质、菱形的判定和性质及勾股定理,掌握对角线互相垂直平分的四边形为菱形是解题的关键.
46.2.5
【分析】
首先根据折叠的性质与矩形的性质,得到AF=AB=5,EF=BE,AD=BC=4;然后在Rt△ADF中,利用勾股定理,求得DF的长,进而得到CF的长;再设CE=x,则EF=BE=4-x,在Rt△CEF中,利用勾股定理列出关于x的方程,求得x的值,最后由BE=BC-CE,即可得到结果.
【详解】
解:由题意可得AF=AB=5,AD=BC=4,EF=BE,
在Rt△ADF中,由勾股定理,得DF===3.
在矩形ABCD中,DC=AB=5,
∴CF=DC-DF=2.
设CE=x,则EF=BE=4-x,
在Rt△CEF中,CE2+CF2=EF2,即x2+22=(4-x)2,
解得x=1.5,
则BE=4-x=2.5.
故答案为2.5.
点睛:本题考查翻折变换、矩形的性质,找出线段间的关系,利用勾股定理列出等量关系式是解题的关键.
47.AD=DC(答案不唯一)
【详解】
试题分析:由四边形ABCD是平行四边形,
添加AD=DC,根据邻边相等的平行四边形是菱形的判定,可使得平行四边形ABCD为菱形;
添加AC⊥BD,根据对角线互相垂直的平行四边形是菱形的判定,可使得平行四边形ABCD为菱形.
答案不唯一.
48.5.
【分析】
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【详解】
解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为5
【点睛】
本题考查轴对称-最短路线问题;菱形的性质.
49.
【详解】
如图,连接AO交EF于点P,
由菱形和折叠对称的性质,知四边形AEOF是菱形,且AP=OP.
∵点A恰好落在菱形的对称中心O处,∴AE=BE.
∵AB=2,∠A=120°,
∴Rt△AEF中,AE=1,∠AEP=30°.
∴EP=.
∴EF=.
50.()n﹣1
【详解】
解:∵四边形ABCD为正方形,
∴AB=BC=1,∠B=90°,∴AC=;
同理可求:AE=,HE=,…,
∴第n个正方形的边长an=.
故答案为.
51.16
【详解】
试题分析:先利用三角形中位线性质得到AB=4,然后根据菱形的性质计算菱形ABCD的周长.
∵E,F分别是AD,BD的中点, ∴EF为△ABD的中位线, ∴AB=2EF=4,
∵四边形ABCD为菱形, ∴AB=BC=CD=DA=4, ∴菱形ABCD的周长=4×4=16.
考点:(1)菱形的性质;(2)三角形中位线定理.
52.24
【详解】
已知对角线的长度,根据菱形的面积计算公式即可计算菱形的面积.
解:根据对角线的长可以求得菱形的面积,
根据S=ab=×6×8=24cm2,
故答案为24.
53.4
【详解】
分析:由□ABCD的周长为26cm,对角线AC、BD相交于点O,若△AOD的周长比△AOB的周长多3cm,可得AB+AD=13cm,AD-AB=3cm,求出AB和AD的长,得出BC的长,再由直角三角形斜边上的中线性质即可求得答案.
详解:∵□ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OD+AD)-(OA+OB+AB)=AD-AB=3cm,
∴AB=5cm,AD=8cm.
∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4cm;
故答案为4.
点睛: 此题考查了平行四边形的性质、直角三角形斜边上的中线性质.熟练掌握平行四边形的性质,由直角三角形斜边上的中线性质求出AE是解决问题的关键.
54.(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3).
【详解】
试题分析:(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论(3)根据等腰直角三角形的性质得到BC=AB=4,AH=BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
试题解析:解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
(2)成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD;
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=AB=4,AH=BC=2,
∴CD=BC=1,CH=BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG==.
考点:四边形综合题.
55.(1)见解析;(2)6
【分析】
(1)根据DB⊥BC,CF⊥AE,得出∠D=∠AEC,再结合∠DBC=∠ECA=90°,且BC=CA,证明△DBC≌△ECA,即可得证;
(2) 由(1)可得△DBC≌△ECA,可得CE=BD,根据BC=AC=12cm AE是BC的中线,即可得出,即可得出答案.
【详解】
证明:(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,且BC=CA,
在△DBC和△ECA中,
∴△DBC≌△ECA(AAS).
∴AE=CD;
(2) 由(1)可得△DBC≌△ECA
∴CE=BD,
∵BC=AC=12cm AE是BC的中线,
∴,
∴BD=6cm.
【点睛】
本题考查了全等三角形的判定和性质,直角三角形斜边上的中线,证明△DBC≌△ECA解题关键.
56.(1)证明见解析;(2)成立,证明见解析.
【详解】
解:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA,
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE
∴∠MEA=∠AFO,
∴Rt△BOE≌ Rt△AOF
∴OE=OF
(2)OE=OF成立
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA
又∵AM⊥BE,
∴∠F+∠MBF=90°=∠E+∠OBE
又∵∠MBF=∠OBE
∴∠F=∠E
∴Rt△BOE≌Rt△AOF
∴OE=OF
57.(1)PB=PQ.证明见解析;(2)PB=PQ.证明见解析.
【详解】
试题分析:(1)过P作PE⊥BC,PF⊥CD,证明Rt△PQF≌Rt△PBE,即可;
(2)证明思路同(1).
试题解析:(1)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
考点: 正方形的判定与性质;全等三角形的判定与性质.
58.60°
【详解】
试题分析:根据正方形和等边三角形的性质可得:∠BAD=90°,∠DAE=60°,根据△BAE为等腰三角形可得:∠ABE=∠AEB=15°,根据正方形的性质可得:∠BCF=45°,∠CBF=90°-15°=75°,根据△BCF的内角和定理可得:∠BFC=180°-45°-75°=60°.
考点:(1)、等腰三角形的性质;(2)、三角形内角和定理;(3)、等边三角形的性质
59.(1)见解析;(2)120°;;(3)见解析
【分析】
(1)证明∠BAC=∠DAE,得出∠BAD=∠CAE,由SAS即可得出结论;
(2)求出∠ACB=∠ACE=30°,由平行线的性质得出∠MEC+∠ECD=180°,即可得出结果;
(3)由△BAD≌△CAE,得出DB=CE,再证明∠ACE=∠EMC,得出ME=EC,推出DB=ME,即可得出结论.
【详解】
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠BAC=180°-2∠ABC,
∵以AD、AE为腰做等腰三角形ADE,
∴AD=AE,
∴∠ADE=∠AED,
∴∠DAE=180°-2∠ADE,
∵∠ADE=∠ABC,
∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS);
(2)解:∵AB=AC,
∴∠ACB=∠ABC=30°,
∵△BAD≌△CAE,
∴∠ABD=∠ACE=30°,
∴∠ACB=∠ACE=30°,
∴∠ECB=∠ACB+∠ACE=60°,
∵EM∥BC,
∴∠MEC+∠ECD=180°,
∴∠MEC=180°﹣60°=120°;
(3)证明:∵△BAD≌△CAE,
∴DB=CE,∠ABD=∠ACE,
∵AB=AC,
∴∠ABD=∠ACB,
∴∠ACB=∠ACE,
∵EM∥BC,
∴∠EMC=∠ACB,
∴∠ACE=∠EMC,
∴ME=EC,
∴DB=ME,
又∵EM∥BD,
∴四边形MBDE是平行四边形.
【点睛】
本题考查了平行四边形的判定、等腰三角形的判定与性质、平行线的性质、全等三角形的判定与性质等知识;熟练掌握全等三角形的判定与性质是解题的关键.
60.(1)相等,垂直;(2)成立,见解析;(3)2.
【分析】
(1)利用SAS证明△ABE≌△CBF,延长CF交AB于点M,证明∠AMC=90°即可;
(2)仿照(1)的证明方法求解即可;
(3)根据题意,得点F在以B为圆心,BF为半径的圆上运动,根据直径最大原理,知道当C,B,F三点一线时,CF最大,此时点E恰好在AB的延长线上,连接DE,利用勾股定理求值即可.
【详解】
(1)如图①,∵正方形ABCD和等腰直角△BEF,
∴BA=BC,∠EBA=∠FBC=90° ,BE=BF,
∴△ABE≌△CBF,
∴AE=CF,
延长CF交AE于点M,
∵△ABE≌△CBF,
∴∠EAB=∠FCB ,
∵∠AFM=∠BFC ,
∴∠AMF=∠FBC=90° ,
∴AE⊥CF,
故答案为:相等,垂直;
(2)结论还成立.理由如下:
如图②,∵正方形ABCD和等腰直角△BEF,
∴BA=BC,∠EBF=∠ABC=90° ,BE=BF,
∴∠EBF-∠ABF =∠ABC-∠ABF,
∴∠EBA =∠FBC,
∴△ABE≌△CBF,
∴AE=CF,
延长CF交AE于点N,交AB于点G,
∵△ABE≌△CBF,
∴∠EAB=∠FCB ,
∵∠AGN=∠BGC ,
∴∠ANG=∠GBC=90° ,
∴AE⊥CF,
故结论成立;
(3)如图③,根据题意,得点F在以B为圆心,BF为半径的圆上运动,根据直径最大原理,知道当C,B,F三点一线时,CF最大,此时点E恰好在AB的延长线上,连接DE,∵AB= 2BF = 4,
∴AE=AB+BE=6,
在直角三角形ADE中,
DE==2.
【点睛】
本题考查了正方形的性质,等腰直角三角形的性质,三角形的全等,勾股定理,直径是圆中的最大的弦,垂直的定义,熟练掌握三角形全等,垂直的证明是解题的关键.
61.(1)见解析
(2)45°,理由见解析
【分析】
(1)根据平行线的性质可得∠ADO=∠ECO,再根据中点定义可得DO=CO,然后可利用ASA证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,由(1)得四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
【详解】
解:(1)∵四边形ABCD是平行四边形
∴AD∥BE
∴∠ADO=∠ECO
又∵O是CD的中点
∴OD=OC
在△AOD和△EOC中
∴△AOD ≌ △EOC (ASA)
(2)45°
由(1)知,OA=OE,OC=OD
∴四边形ACED是平行四边形
∴AD=CE
又∵四边形ABCD是平行四边形
∴AD=BC
∴BC =CE
当∠B=∠AEB=45°时,
且
∴四边形ACED是正方形.
【点睛】
本题考查了全等三角形的判定与性质,以及正方形的判定,关键是掌握对角线互相垂直且相等的平行四边形是正方形.
62.(1)证明见解析;(2)
【详解】
(1)如图1中,结论:△BCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠CBE=∠AEB,
∵EB平分∠AEC,
∴∠AEB=∠BEC,
∴∠CBE=∠BEC,
∴CB=CE,
∴△CBE是等腰三角形;
(2)如图2中,∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠D=90°,BC=AD=5,
在Rt△ECD中,∵∠D=90°,ED=AD-AE=4,EC=BC=5,
在中,∵∠A=90°,AB=3.AE=1,
63.(1)见详解;(2)
【分析】
(1)先证明AB∥CE,再推出∠ADB=∠OBC=60°,从而得AD∥BC,进而得到结论;
(2)根据勾股定理求出AO的长,再根据平行四边形的面积公式,即可求解.
【详解】
(1)证明:∵∠OAB=90°,
∴AB⊥x轴,
∵y轴⊥x轴,
∴AB∥y轴,即AB∥CE,
∵∠AOB=30°,
∴∠OBA=60°,
∵∠OAB=90°,D是OB的中点,
∴DB=DO= =4,
∵∠AOB=30°,
∴AB= =4,
∵DB=DO=AB =4,
∴∠BDA=∠BAD=(180°-60°)÷2=60°,
∵△OBC是等边三角形,
∴∠OBC=60°,
∴∠ADB=∠OBC,
即AD∥BC,
∴四边形ABCE是平行四边形;
(2)在直角△OAB中,AB=4,BO=8,
∴AO=,
∴平行四边形ABCE的面积=AB AO=.
【点睛】
本题主要考查直角三角形的性质,等边三角形的性质,勾股定理以及平行四边形的判定定理,熟练掌握平行四边形的判定定理是解题的关键.
64.(1)见解析;(2)
【分析】
(1)证明四边形CFBD是平行四边形,再证明∠1=90°,即可判定四边形CFBD是菱形.
(2)根据菱形的性质求得EF=1,再由勾股定理求得CE=3,由三角形的中位线定理可得AC=2,再由勾股定理即可求得.
【详解】
(1)证明:∵E是边BC的中点,
∴BE=EC,
∵ DE=EF,BE=EC,
∴四边形CFBD是平行四边形,
∵D是AB边中点,E是BC中点,
∴DE∥AC,
∴∠1=∠ACB=90°,
∴四边形CFBD是菱形.
(2)∵四边形CFBD是菱形,
∴∠CEF=90°.
∵DF=2,
∴EF=1,
∵,
∴由勾股定理得,CE=3,
∵D,E分别是边AB,BC的中点,DE=1,
∴AC=2,
∵∠ACB=90°,
由勾股定理得.
【点睛】
本题考查了菱形的判定与性质、勾股定理等知识,熟练运用相关知识是解决问题的关键.
65.(1)证明见解析;(2)四边形DEBF是平行四边形,理由见解析.
【详解】
分析:(1)利用平行四边形ABCD的对角相等,对边相等的性质推知∠A=∠C,AD=BC;然后根据全等三角形的判定定理AAS证得结论;
(2)由“对边平行且相等的四边形是平行四边形”推知四边形DEBF是平行四边形.
详解:(1)证明:∵四边形ABCD为平行四边形,
∴∠A=∠C,AD=BC,
在△ADE与△CBF中,
∴△ADE≌△CBF(ASA);
(2)四边形DEBF是平行四边形.理由如下:
∵DF∥EB,又由△ADE≌△CBF,知AE=CF,
∴AB﹣AE=CD﹣CF,即DF=EB.
∴四边形DEBF是平行四边形
点睛:本题考查了全等三角形的判定与性质、平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
66.(1)见解析;(2)能,;(3)或,理由见解析
【分析】
(1)由已知条件可得Rt△CDF中∠C=30°,即可知DF=CD=AE=2t;
(2)由DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;
(3)分∠EDF=90°、∠DEF=90°两种情况,根据直角三角形的性质列出算式,计算即可.
【详解】
(1)证明:∵在中,,
,,
∴.
∵,,
在直角中,,
∴,
∴;
(2)∵,,
∴四边形是平行四边形,
当时,四边形是菱形,
即,
解得:,
即当时,平行四边形是菱形;
(3)当时是直角三角形();
当时,是直角三角形().
理由如下:
当时,
∴
∴
∵,
∴,
∴,
∴,
∴时,.
当时,,
∵四边形是平行四边形,
∴,
∴,
∴是直角三角形,,
∵,
∴,
∴,,
,
∴,
解得.
综上所述,当时是直角三角形();当时,是直角三角形().
【点睛】
本题是四边形综合题,考查了直角三角形的性质、平行四边形的判定与性质、菱形的性质、含角的直角三角形的性质等知识点,熟练掌握平行四边形、菱形的判定是解题的关键.
67.(1)5;(2)见解析
【分析】
(1)依据,,可得是等腰直角三角形,结合求出,再根据勾股定理,即可求解的长;
(2)连接GE,过A作,交BG于P,连接PE,利用正方形的判定方法可证得四边形是正方形,即可得到,,进而得出,依据,,即可得到.
【详解】
(1)解:∵,,
∴,
∴,
∴是等腰直角三角形,
∴.
∵,
∴,
∵,
∴.
(2)如图,连接GE,过A作,交BG于P,连接PE,
∵,,
∴,
∴BG是AE的垂直平分线,
∴,
∵,
∴是等腰直角三角形,即,
是等腰直角三角形,即,
∴,
∵,
∴四边形是正方形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
又∵,
∴.
【点睛】
本题考查了平行四边形的性质、正方形的判定与性质以及全等三角形的判定与性质等知识,掌握特殊四边形的判定与性质并能灵活运用所学知识是解题的关键.
68.(1)见解析;(2)见解析;(3),理由见解析.
【分析】
(1)根据题意按步骤画图即可;
(2)根据平行线的性质和角平分线的定义得出,则,进而有,然后利用一组对边平行且相等的四边形是平行四边形即可证明;
(3)根据菱形的性质有,然后利用等腰三角形的性质和平行线的性质即可求解.
【详解】
(1)补全图形如下:
(2) ,
.
,
.
∵AD平分,
,
,
,
.
,
∴四边形BEFG是平行四边形;
(3),理由如下:
若四边形BEFG是菱形,则有,
,
,
.
∵四边形BEFG是平行四边形,
,
.
【点睛】
本题主要考查平行四边形的判定及性质,菱形的性质,掌握平行四边形的判定及性质和菱形的性质是解题的关键.
答案第1页,共2页
