华东师大版八年级下册数学 18.1 平行四边形的性质 课件(共15张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 18.1 平行四边形的性质 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
18.1 平行四边形的性质
生活中的平行四边形形象
(墙砖)
(升降机)
(停车位)
(楼梯)
你能列举生活中平行四边形形象的例子吗?
教学目标:
1.在对平行四边形原有认识的基础上,进一步理解平行四边形的概念。
2、通过实验、观察,发现平行四边形对边相等,对角相等的性质,能用演绎推理的方法加以证明,会运用这些性质进行简单的计算。
教学重点
1、理解平行四边形的概念,探索并证明平行四边形的性质。
2、能根据平行四边形的性质解决简单的数学问题。
教学难点
1、平行四边形的性质的探索与证明。
1
2
4
5
3
8
9
6
7
你能从中找到平行四边形吗?
明确概念
A
B
C
D
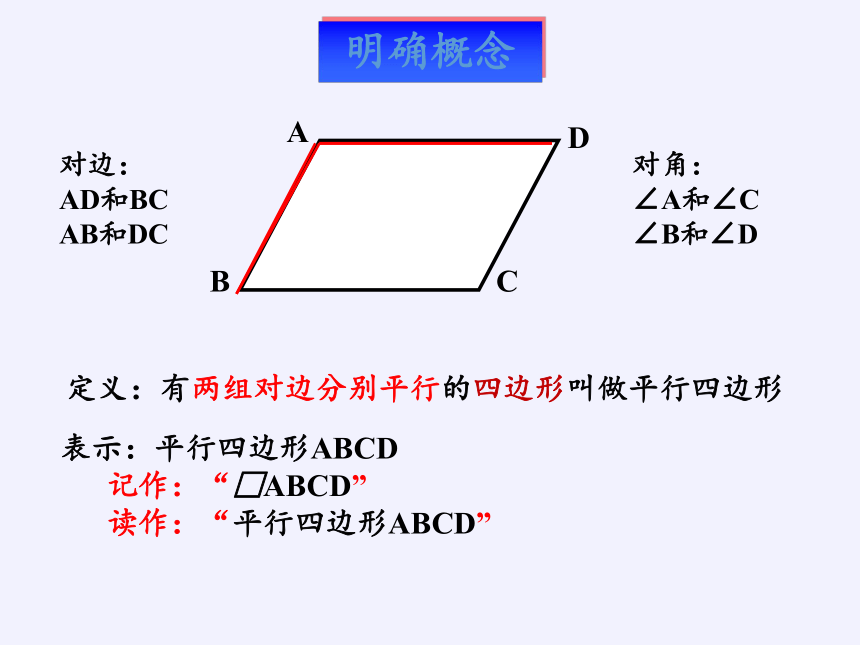
定义:有两组对边分别平行的四边形叫做平行四边形
对边:
AD和BC
AB和DC
对角:
∠A和∠C
∠B和∠D
表示:平行四边形ABCD
记作:“□ABCD”
读作:“平行四边形ABCD”
探究性质
想一想:
除此之外,平行四边形的对边之间、对角之间还有什么数量关系呢
根据定义,我们可以知道平行四边形有什么性质
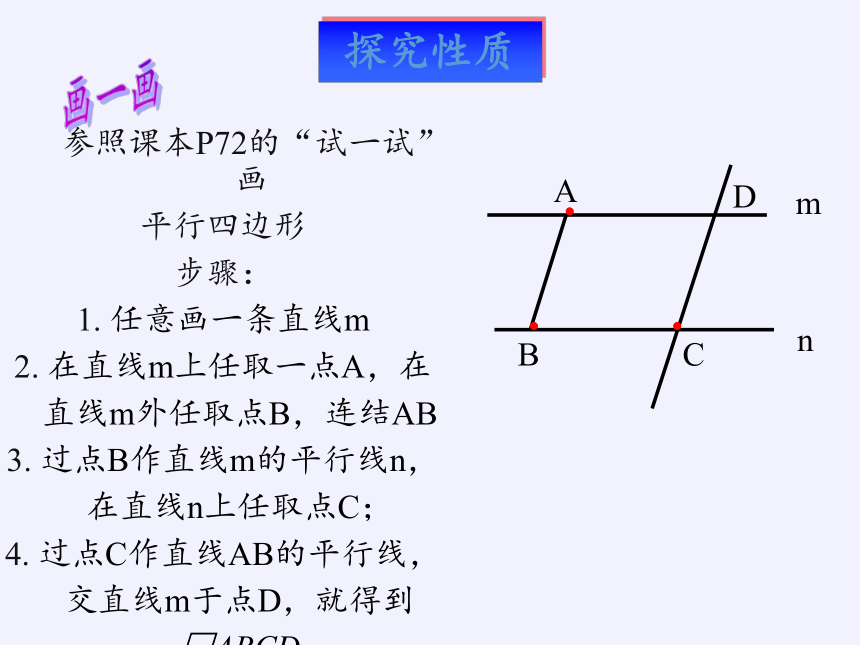
参照课本P72的“试一试”画
平行四边形
步骤:
1. 任意画一条直线m
2. 在直线m上任取一点A,在
直线m外任取点B,连结AB
3. 过点B作直线m的平行线n,
在直线n上任取点C;
4. 过点C作直线AB的平行线,
交直线m于点D,就得到
□ABCD
探究性质
m
A
B
C
D
n
画一画
请同学们把□ABCD剪下来,放在学案的空白处,并沿着□ABCD的边沿,画出一个四边形,记为EFGH.
剪一剪:
探究性质
B
A
D
C
F
E
H
G
各小组按下列步骤操作:
(1)在□ABCD中,连结AC、BD,
他们的交点记为点O.
(2)用图钉穿过点O,将□ABCD绕点O旋转180°.
(3)观察并思考以下问题:
①旋转后的平行四边形与另一个平行四边形是否重合?由此可知平行四边形具有什么样的对称性?
②由此你们能发现平行四边形的对边、对角之间有什么数量关系?
做一做:
探究性质
E
F
H
G
O
A
B
C
D
1.证明: 平行四边形的对边相等.
D
A
B
C
已知: 如图,□ABCD .
求证:AB=CD,AD=CB.
想一想:证明边相等有哪些方法
2.证明: 平行四边形的对角相等.
证明:连结BD.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.(平行四边形的两组对边分别平行),
∴ ∠ABD= ∠CDB, ∠ADB= ∠CBD.
∵ BD=DB,
∴ △ABD≌△CDB(A.S.A.) .
∴ AB=CD,AD=CB.
证明性质
平行四边形问题可以转化为三角形问题来解决
例:如图,用一根56cm长的铁丝围成一个□ABCD.
(1)如果AB=18cm,求其余三条边的长;
(2)如果已知一个内角的度数,能否求出其他各内
角的大小?
若能,请你写出一个内角的度数,然后求出其他各内角的大小.
平行四边形的邻角有什么关系
A
B
C
D
应用性质
平行四边形的邻角互补.
已知: □ABCD.
1. 若AB+BC=10,则□ABCD的周长为 .
2. 若∠A+∠C=100°,则∠B=____,∠C=____.
3. 若AD∶CD =3∶4,周长是42,则AB=____,BC=____.
4. ∠A∶∠B∶∠C∶∠D的值可以是( )
A. 1∶2∶3∶4 B. 1∶2∶2∶1
C. 1∶1∶2∶2 D. 2∶1∶2∶1
5. ∠A:∠B=5:4,则∠C、∠D的度数分别为( )
A. 100°和80° B. 100°和50°
C. 120°和60° D. 135°和45°
巩固性质
20
130°
50°
12
9
D
A
1. 这节课我们主要学行四边形的什么性质?
总结反思
1. 书面作业:课本第75页练习第1、3题
作业布置
谢 谢
18.1 平行四边形的性质
生活中的平行四边形形象
(墙砖)
(升降机)
(停车位)
(楼梯)
你能列举生活中平行四边形形象的例子吗?
教学目标:
1.在对平行四边形原有认识的基础上,进一步理解平行四边形的概念。
2、通过实验、观察,发现平行四边形对边相等,对角相等的性质,能用演绎推理的方法加以证明,会运用这些性质进行简单的计算。
教学重点
1、理解平行四边形的概念,探索并证明平行四边形的性质。
2、能根据平行四边形的性质解决简单的数学问题。
教学难点
1、平行四边形的性质的探索与证明。
1
2
4
5
3
8
9
6
7
你能从中找到平行四边形吗?
明确概念
A
B
C
D
定义:有两组对边分别平行的四边形叫做平行四边形
对边:
AD和BC
AB和DC
对角:
∠A和∠C
∠B和∠D
表示:平行四边形ABCD
记作:“□ABCD”
读作:“平行四边形ABCD”
探究性质
想一想:
除此之外,平行四边形的对边之间、对角之间还有什么数量关系呢
根据定义,我们可以知道平行四边形有什么性质
参照课本P72的“试一试”画
平行四边形
步骤:
1. 任意画一条直线m
2. 在直线m上任取一点A,在
直线m外任取点B,连结AB
3. 过点B作直线m的平行线n,
在直线n上任取点C;
4. 过点C作直线AB的平行线,
交直线m于点D,就得到
□ABCD
探究性质
m
A
B
C
D
n
画一画
请同学们把□ABCD剪下来,放在学案的空白处,并沿着□ABCD的边沿,画出一个四边形,记为EFGH.
剪一剪:
探究性质
B
A
D
C
F
E
H
G
各小组按下列步骤操作:
(1)在□ABCD中,连结AC、BD,
他们的交点记为点O.
(2)用图钉穿过点O,将□ABCD绕点O旋转180°.
(3)观察并思考以下问题:
①旋转后的平行四边形与另一个平行四边形是否重合?由此可知平行四边形具有什么样的对称性?
②由此你们能发现平行四边形的对边、对角之间有什么数量关系?
做一做:
探究性质
E
F
H
G
O
A
B
C
D
1.证明: 平行四边形的对边相等.
D
A
B
C
已知: 如图,□ABCD .
求证:AB=CD,AD=CB.
想一想:证明边相等有哪些方法
2.证明: 平行四边形的对角相等.
证明:连结BD.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.(平行四边形的两组对边分别平行),
∴ ∠ABD= ∠CDB, ∠ADB= ∠CBD.
∵ BD=DB,
∴ △ABD≌△CDB(A.S.A.) .
∴ AB=CD,AD=CB.
证明性质
平行四边形问题可以转化为三角形问题来解决
例:如图,用一根56cm长的铁丝围成一个□ABCD.
(1)如果AB=18cm,求其余三条边的长;
(2)如果已知一个内角的度数,能否求出其他各内
角的大小?
若能,请你写出一个内角的度数,然后求出其他各内角的大小.
平行四边形的邻角有什么关系
A
B
C
D
应用性质
平行四边形的邻角互补.
已知: □ABCD.
1. 若AB+BC=10,则□ABCD的周长为 .
2. 若∠A+∠C=100°,则∠B=____,∠C=____.
3. 若AD∶CD =3∶4,周长是42,则AB=____,BC=____.
4. ∠A∶∠B∶∠C∶∠D的值可以是( )
A. 1∶2∶3∶4 B. 1∶2∶2∶1
C. 1∶1∶2∶2 D. 2∶1∶2∶1
5. ∠A:∠B=5:4,则∠C、∠D的度数分别为( )
A. 100°和80° B. 100°和50°
C. 120°和60° D. 135°和45°
巩固性质
20
130°
50°
12
9
D
A
1. 这节课我们主要学行四边形的什么性质?
总结反思
1. 书面作业:课本第75页练习第1、3题
作业布置
谢 谢
