2021-2022学年(下)高二年级开学考数学试卷word版含答案
文档属性
| 名称 | 2021-2022学年(下)高二年级开学考数学试卷word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 704.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 16:36:25 | ||
图片预览




文档简介
高二年级开学考
姓名:___________班级:___________成绩:____
一、单选题
1.设集合,则等于( )
A. B. C. D.
2.已知复数满足,则复数( )
A. B. C. D.
3.已知等差数列中,,,则( )
A. B. C. D.
4.等比数列的公比为q,设甲:,乙:数列是递增数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
5.2021年10月16日0时23分,搭载神舟十三号载人飞船的长征二号F遥十三运载火箭,在酒泉卫星发射中心按照预定时间精准点火发射,顺利将翟志刚、王亚平、叶光富3名航天员送入太空,飞行乘组状态良好,发射取得圆满成功.火箭在发射时会产生巨大的噪音,若所有声音的声强级d(x)(单位:)与声强x(单位:)满足.火箭发射时的声强级约为140,人交谈时的声强级约为50,那么火箭发射时的声强与人交谈时的声强的比值约为( )
A. B. C. D.
6.2021年7月20日郑州特大暴雨引发洪灾,各地志愿者积极赴郑州救灾.某志愿小组共6人,随机派两人去执行某次抢救任务,则甲乙两人没有同去的概率为( )
A. B. C. D.
7.已知是双曲线C的两个焦点,P为C上一点,且,则C的离心率为( )
A. B. C. D.
8.若,则( )
A. B. C. D.
9.如图,塔底部为点,若两点相距为100并且与点在同一水平线上,现从两点测得塔顶的仰角分别为和,则塔的高约为(精确到0.1,,)
A.36.5 B.115.6 C.120.5 D.136.5
10.已知,,,若不等式恒成立,则实数的取值范围是( )
A. B. C. D.
11.已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
12.定义在上的偶函数的图象关于直线对称,当时,.若方程且根的个数大于3,则实数的取值范围为( )
A. B. C. D.
二、填空题
13.已知直线x-y-1=0和圆交于A,B两点,则|AB|=________.
14.已知向量,,且,则___________.
15.已知直线与椭圆相交于两点,椭圆的两个焦点分别是,线段的中点为,则的面积为________.
16.已知是定义在(0,3)上的函数,的图象如图所示,则不等式的解集是______.
三、解答题
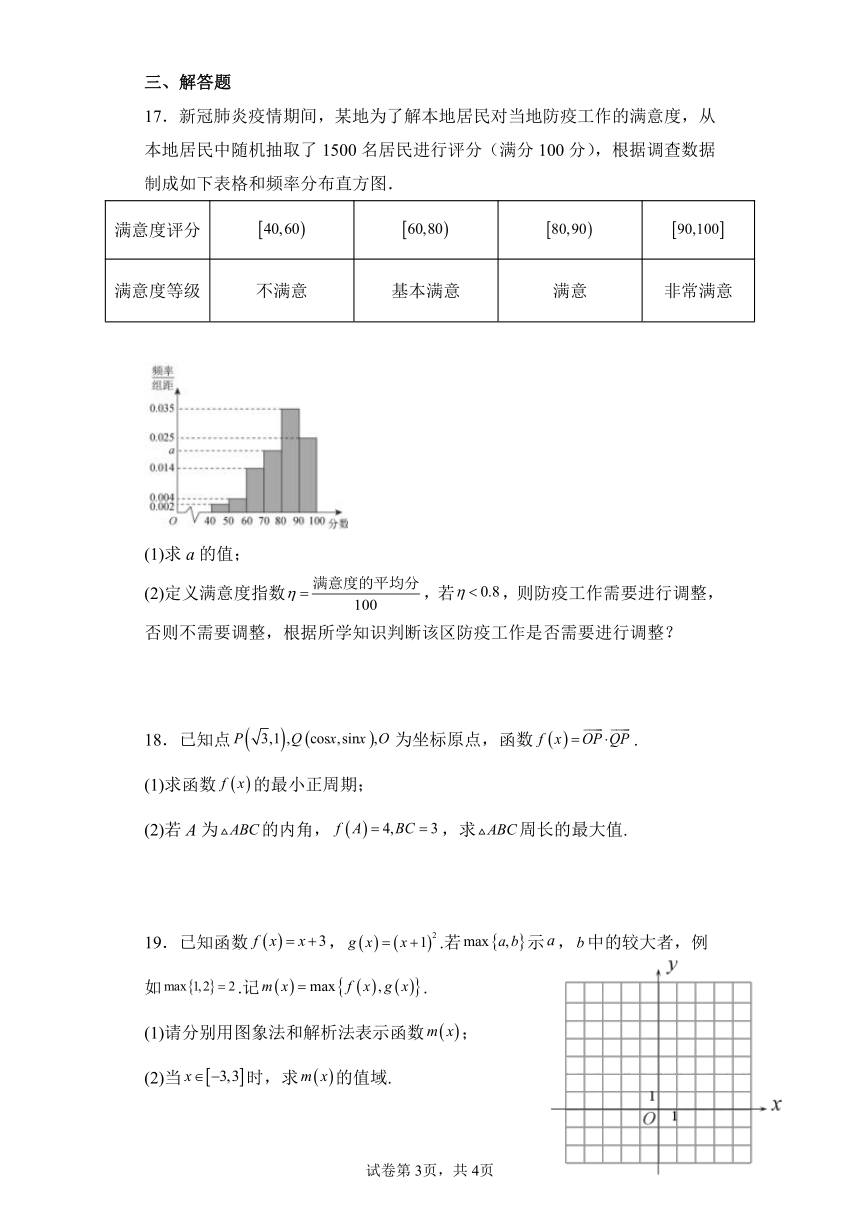
17.新冠肺炎疫情期间,某地为了解本地居民对当地防疫工作的满意度,从本地居民中随机抽取了1500名居民进行评分(满分100分),根据调查数据制成如下表格和频率分布直方图.
满意度评分
满意度等级 不满意 基本满意 满意 非常满意
(1)求a的值;
(2)定义满意度指数,若,则防疫工作需要进行调整,否则不需要调整,根据所学知识判断该区防疫工作是否需要进行调整?
18.已知点为坐标原点,函数.
(1)求函数的最小正周期;
(2)若A为的内角,,求周长的最大值.
19.已知函数,.若示,中的较大者,例如.记.
(1)请分别用图象法和解析法表示函数;
(2)当时,求的值域.
20.如图,直三棱柱中,四边形是正方形,..、分别是、的中点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
21.已知数列{}的前n项和满足:.
(1)求数列{}的前3项;
(2)求证:数列是等比数列;
(3)求数列的前n项和.
22.已知抛物线y2=2px(p>0)的焦点F到准线的距离为2.
(1)求抛物线的方程;
(2)过点P(1,1)作两条动直线l1,l2分别交抛物线于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,试判断直线m是否经过定点,并说明理由.试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
因为,
又,故可得.
2.B
由,得,所以.
3.A
由等差中项的性质可得.
4.B
由题,当数列为时,满足,
但是数列不是递增数列,所以甲不是乙的充分条件.
若数列是递增数列,则必有成立,若不成立,则会出现一正一负的情况,是矛盾的,则成立,所以甲是乙的必要条件.
5.A
由题意,,则
火箭发射时的声强级约为140,人交谈时的声强级约为50,
则火箭发射时的声强约为,人交谈时的声强约为,
所以火箭发射时的声强与人交谈时的声强的比值约为
6.C
6个人即为1,2,3,4,5,6代表,派遣的可能情形有:
,,,,,,,,,,,,,,,共15种情形,甲乙同去占一种情形,
则不同去的概率为..
7.D
因为,由双曲线的定义可得,
所以,;
因为,由余弦定理可得,
整理可得,所以,即.
8.C
由题设,,
又.
9.D
试题分析:在中,在,
10.A
∵,,,
∴,
当且仅当,即,时取等号.
∵不等式恒成立,
∴,解得.
11.C
,为等腰直角三角形,,
则外接圆的半径为,又球的半径为1,
设到平面的距离为,
则,
所以.
12.D
由题设,,即,
所以是周期为4的函数,
若,则,故,
所以,
要使且根的个数大于3,即与交点个数大于3个,又恒过,
当时,在上,在上且在上递减,此时与只有一个交点,所以.
综上,、的图象如下所示,
要使交点个数大于3个,则,
可得.
13.2
圆(x-1)2+y2=1的半径r=1,圆心(1,0)
圆心到直线的距离,则直线经过圆的圆心,
所以弦长|AB|=2r=2.
14.(或)
由题意可得,
因为,所以,即,解得.
15.
设,,则两式相减,得,
因为直线的斜率为,则,线段的中点为
所以,解得.
因为,所以,
故的面积为.
16.
由图象可知:时,;当时,.
又余弦函数在时,时,
当时,,
17.(1)
(2)不需要
【解析】(1),解得.
(2).
故不需要进行调整.
18.(1)
(2)
【解析】(1)故的最小正周期,
(2)
,解得:,而,故,故,所以;
又,设角A,B,C所对的边分别为a,b,c,由余弦定理得:,所以,又,故,
解得:,当且仅当时等号成立,
故,即周长的最大值为.
19.(1)图像法如图所示:
解析式为
(2)
【解析】
(1)
在同一直角坐标系中,作出函数,图象如下:
则的图象如下图实线部分:
由图知,.
(2)
由图知,在上单调递诚,在上单调递增,
且,,,
所以当时,的值域为.
20.(1)证明见解析
(2)
【解析】
(1)
取的中点,连接、,
∵四边形为正方形,则且,
为的中点,且,
分别为、的中点,则且,
且,故四边形为平行四边形,从而.
而平面,平面,平面;
(2)
以点为原点,为轴,为轴,为轴建立如图所示的空间直角坐标系.
则、、、.
从而,,.
设平面的法向量为,由得,
取,则,
,
∴直线与平面所成角的正弦值为.
21.(1)
(2)
【解析】
(1)当时,,
得
即,即
所以数列是首项为2,公比为2的等比数列,故.
(2)由(1)知,则
(1)
(2)
(1)-(2)得
所以
22.(1)y2=4x;
(2)直线m恒过定点(,),理由见解析.
【解析】
(1)由题意得该抛物线焦点到准线的距离为-(-)=p=2,
所以该抛物线的方程为y2=4x.
(2)
①当直线l1, l2的斜率都存在时,设直线l1:,直线l2:y-1=k2(x-1),
由,消去y得,显然,
设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=,
,,
则以AB为直径的圆的方程为:,
,
即++=0,
同理,以CD为直径的圆的方程为:++=0,
∴两圆公共弦所在的直线m的方程为:.
令,解得,所以直线恒过定点(,).
②当直线l1,l2的斜率中有一个不存在时,由对称性不妨设l1的斜率不存在,l2的斜率为k2,
则以AB为直径的圆的方程为:,
以CD为直径的圆的方程为:++=0,
所以两圆公共弦所在的直线m的方程为:,
此时直线m恒过定点(,),综上得:直线m恒过定点(,).
答案第1页,共2页
答案第1页,共2页
姓名:___________班级:___________成绩:____
一、单选题
1.设集合,则等于( )
A. B. C. D.
2.已知复数满足,则复数( )
A. B. C. D.
3.已知等差数列中,,,则( )
A. B. C. D.
4.等比数列的公比为q,设甲:,乙:数列是递增数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
5.2021年10月16日0时23分,搭载神舟十三号载人飞船的长征二号F遥十三运载火箭,在酒泉卫星发射中心按照预定时间精准点火发射,顺利将翟志刚、王亚平、叶光富3名航天员送入太空,飞行乘组状态良好,发射取得圆满成功.火箭在发射时会产生巨大的噪音,若所有声音的声强级d(x)(单位:)与声强x(单位:)满足.火箭发射时的声强级约为140,人交谈时的声强级约为50,那么火箭发射时的声强与人交谈时的声强的比值约为( )
A. B. C. D.
6.2021年7月20日郑州特大暴雨引发洪灾,各地志愿者积极赴郑州救灾.某志愿小组共6人,随机派两人去执行某次抢救任务,则甲乙两人没有同去的概率为( )
A. B. C. D.
7.已知是双曲线C的两个焦点,P为C上一点,且,则C的离心率为( )
A. B. C. D.
8.若,则( )
A. B. C. D.
9.如图,塔底部为点,若两点相距为100并且与点在同一水平线上,现从两点测得塔顶的仰角分别为和,则塔的高约为(精确到0.1,,)
A.36.5 B.115.6 C.120.5 D.136.5
10.已知,,,若不等式恒成立,则实数的取值范围是( )
A. B. C. D.
11.已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
12.定义在上的偶函数的图象关于直线对称,当时,.若方程且根的个数大于3,则实数的取值范围为( )
A. B. C. D.
二、填空题
13.已知直线x-y-1=0和圆交于A,B两点,则|AB|=________.
14.已知向量,,且,则___________.
15.已知直线与椭圆相交于两点,椭圆的两个焦点分别是,线段的中点为,则的面积为________.
16.已知是定义在(0,3)上的函数,的图象如图所示,则不等式的解集是______.
三、解答题
17.新冠肺炎疫情期间,某地为了解本地居民对当地防疫工作的满意度,从本地居民中随机抽取了1500名居民进行评分(满分100分),根据调查数据制成如下表格和频率分布直方图.
满意度评分
满意度等级 不满意 基本满意 满意 非常满意
(1)求a的值;
(2)定义满意度指数,若,则防疫工作需要进行调整,否则不需要调整,根据所学知识判断该区防疫工作是否需要进行调整?
18.已知点为坐标原点,函数.
(1)求函数的最小正周期;
(2)若A为的内角,,求周长的最大值.
19.已知函数,.若示,中的较大者,例如.记.
(1)请分别用图象法和解析法表示函数;
(2)当时,求的值域.
20.如图,直三棱柱中,四边形是正方形,..、分别是、的中点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
21.已知数列{}的前n项和满足:.
(1)求数列{}的前3项;
(2)求证:数列是等比数列;
(3)求数列的前n项和.
22.已知抛物线y2=2px(p>0)的焦点F到准线的距离为2.
(1)求抛物线的方程;
(2)过点P(1,1)作两条动直线l1,l2分别交抛物线于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,试判断直线m是否经过定点,并说明理由.试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
因为,
又,故可得.
2.B
由,得,所以.
3.A
由等差中项的性质可得.
4.B
由题,当数列为时,满足,
但是数列不是递增数列,所以甲不是乙的充分条件.
若数列是递增数列,则必有成立,若不成立,则会出现一正一负的情况,是矛盾的,则成立,所以甲是乙的必要条件.
5.A
由题意,,则
火箭发射时的声强级约为140,人交谈时的声强级约为50,
则火箭发射时的声强约为,人交谈时的声强约为,
所以火箭发射时的声强与人交谈时的声强的比值约为
6.C
6个人即为1,2,3,4,5,6代表,派遣的可能情形有:
,,,,,,,,,,,,,,,共15种情形,甲乙同去占一种情形,
则不同去的概率为..
7.D
因为,由双曲线的定义可得,
所以,;
因为,由余弦定理可得,
整理可得,所以,即.
8.C
由题设,,
又.
9.D
试题分析:在中,在,
10.A
∵,,,
∴,
当且仅当,即,时取等号.
∵不等式恒成立,
∴,解得.
11.C
,为等腰直角三角形,,
则外接圆的半径为,又球的半径为1,
设到平面的距离为,
则,
所以.
12.D
由题设,,即,
所以是周期为4的函数,
若,则,故,
所以,
要使且根的个数大于3,即与交点个数大于3个,又恒过,
当时,在上,在上且在上递减,此时与只有一个交点,所以.
综上,、的图象如下所示,
要使交点个数大于3个,则,
可得.
13.2
圆(x-1)2+y2=1的半径r=1,圆心(1,0)
圆心到直线的距离,则直线经过圆的圆心,
所以弦长|AB|=2r=2.
14.(或)
由题意可得,
因为,所以,即,解得.
15.
设,,则两式相减,得,
因为直线的斜率为,则,线段的中点为
所以,解得.
因为,所以,
故的面积为.
16.
由图象可知:时,;当时,.
又余弦函数在时,时,
当时,,
17.(1)
(2)不需要
【解析】(1),解得.
(2).
故不需要进行调整.
18.(1)
(2)
【解析】(1)故的最小正周期,
(2)
,解得:,而,故,故,所以;
又,设角A,B,C所对的边分别为a,b,c,由余弦定理得:,所以,又,故,
解得:,当且仅当时等号成立,
故,即周长的最大值为.
19.(1)图像法如图所示:
解析式为
(2)
【解析】
(1)
在同一直角坐标系中,作出函数,图象如下:
则的图象如下图实线部分:
由图知,.
(2)
由图知,在上单调递诚,在上单调递增,
且,,,
所以当时,的值域为.
20.(1)证明见解析
(2)
【解析】
(1)
取的中点,连接、,
∵四边形为正方形,则且,
为的中点,且,
分别为、的中点,则且,
且,故四边形为平行四边形,从而.
而平面,平面,平面;
(2)
以点为原点,为轴,为轴,为轴建立如图所示的空间直角坐标系.
则、、、.
从而,,.
设平面的法向量为,由得,
取,则,
,
∴直线与平面所成角的正弦值为.
21.(1)
(2)
【解析】
(1)当时,,
得
即,即
所以数列是首项为2,公比为2的等比数列,故.
(2)由(1)知,则
(1)
(2)
(1)-(2)得
所以
22.(1)y2=4x;
(2)直线m恒过定点(,),理由见解析.
【解析】
(1)由题意得该抛物线焦点到准线的距离为-(-)=p=2,
所以该抛物线的方程为y2=4x.
(2)
①当直线l1, l2的斜率都存在时,设直线l1:,直线l2:y-1=k2(x-1),
由,消去y得,显然,
设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=,
,,
则以AB为直径的圆的方程为:,
,
即++=0,
同理,以CD为直径的圆的方程为:++=0,
∴两圆公共弦所在的直线m的方程为:.
令,解得,所以直线恒过定点(,).
②当直线l1,l2的斜率中有一个不存在时,由对称性不妨设l1的斜率不存在,l2的斜率为k2,
则以AB为直径的圆的方程为:,
以CD为直径的圆的方程为:++=0,
所以两圆公共弦所在的直线m的方程为:,
此时直线m恒过定点(,),综上得:直线m恒过定点(,).
答案第1页,共2页
答案第1页,共2页
同课章节目录
