广东省梅县东山中学2012-2013学年高二上学期期中数学理试题
文档属性
| 名称 | 广东省梅县东山中学2012-2013学年高二上学期期中数学理试题 |  | |
| 格式 | zip | ||
| 文件大小 | 249.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-12 17:22:19 | ||
图片预览




文档简介
广东梅县东山中学2012-2013学年度第一学期期中考试
高二理科数学试题
一、选择题:(8×5分=40分)
1.下列说法正确的是( )
A. 平行于同一平面的两条直线平行 B.与某一平面成等角的两条直线平行
C. 垂直于同一平面的两条直线平行 D.垂直于同一直线的两条直线平行
2.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( ).
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1
D.异面直线AD与CB1角为60°
3. 一个长方体,其正视图面积为,侧视图面积为,俯视图面积为,则长方体的对角线长为( )
A. B. C.6 D.
4.直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则( )
A.a=2,b=5; B.a=2,b=; C.a=,b=5; D.a=,b=
5.直线与直线3x+4y-15=0垂直,与圆相切,则直线的方程是( )
A.4x-3y-6=0 B.4x-3y-66=0
C.4x-3y-6=0或4x-3y-66=0 D.4x-3y-15=0
6. 已知,若三向量共面,则实数λ等于 ( )
A B C D
7.线段AB与x轴平行,且|AB|=5 , 若点A的坐标为(2,1) , 则点B的坐标为(??? )
A. (2,-3)或(2,7)?????? B. (2,-3)或(2,5)?????
C.(-3,1)或(7,1)?????? ? D.(-3,1)或(5,1)
8.异面直线a,b所成的角60°,直线a⊥c,则直线b与c所成的角的范围为( ).
A.[30°,90°] B.[60°,90°]
C.[30°,60°] D.[30°,120°]
二、填空题(6×5分=30分)
9. 若一个球的体积为,则它的表面积为________________
10. 直线被圆截得弦长为__________
11.过圆x2+y2-6x+4y-3=0的圆心,且平行于x+2y+11=0的直线方程是___________
?
12. 已知向量,满足,, 与的夹角为60°,则= __
13.如图2,在正三棱柱中,已知在棱上,且,若与平面所成的角为,则 .
14.在平面直角坐标系中,设三角形ABC 的顶点分别为A(0,a),B(b,0),C (c,0) ,点P(0,p)在线段AO 上(异于端点),设a,b,c, p 均为非零实数,直线BP,CP 分别交AC , AB 于点E ,F ,一同学已正确算的OE的方程:,请你求OF的方程: ____________________。
三、解答题:解答须写出文字说明、证明过程和演算步骤。
15.
16.已知直线经过直线与直线的交点,且垂直于直线.(1)求直线的方程;(2)求直线与两坐标轴围成的三角形的面积.
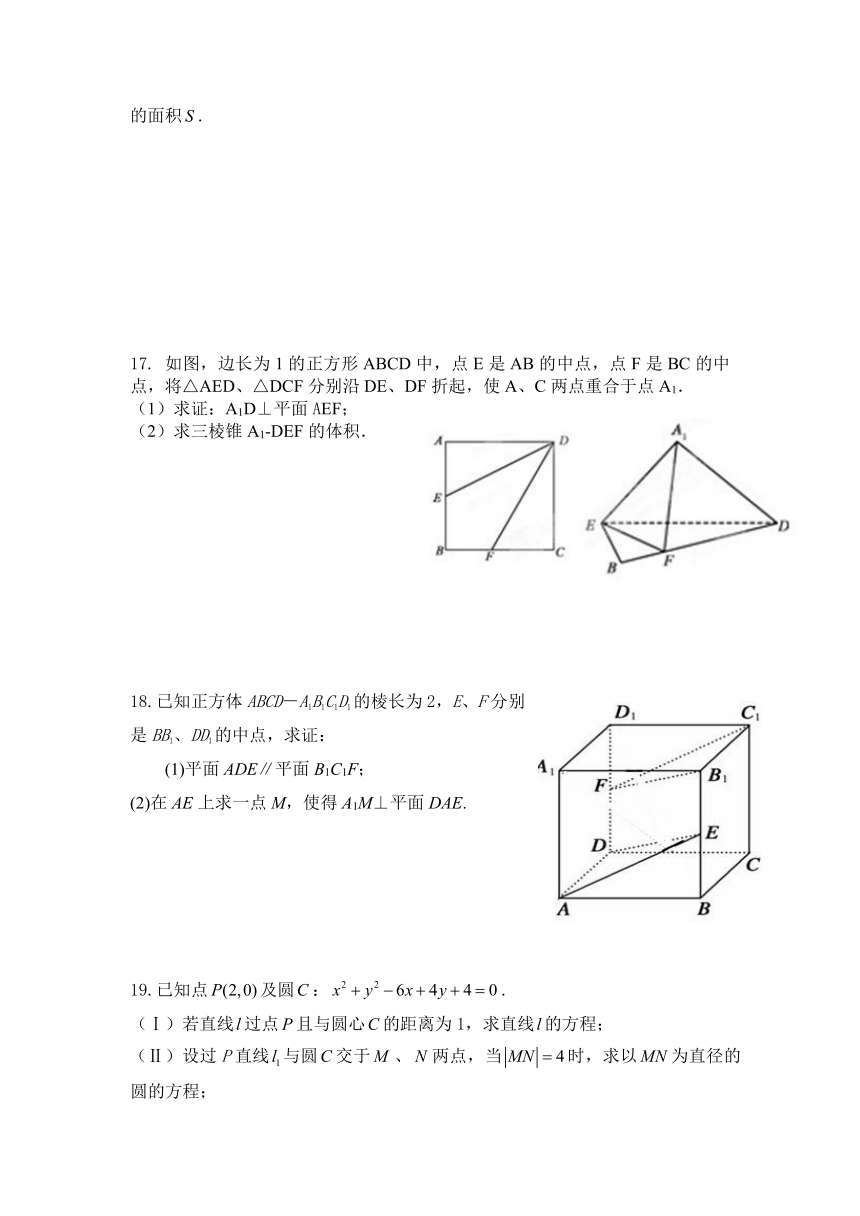
17. 如图,边长为1的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1. (1)求证:A1D⊥平面AEF; (2)求三棱锥A1-DEF的体积.
18.已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:
(1)平面ADE∥平面B1C1F;
(2)在AE上求一点M,使得A1M⊥平面DAE.
19.已知点及圆:.
(Ⅰ)若直线过点且与圆心的距离为1,求直线的方程;
(Ⅱ)设过P直线与圆交于、两点,当时,求以为直径的圆的方程;
(Ⅲ)设直线与圆交于,两点,是否存在实数,使得过点的直线垂直平分弦?若存在,求出实数的值;若不存在,请说明理由.
20.如图,已知四棱锥P-ABCD,PB⊥AD,△PAD是边长2的正三角形,底面ABCD为菱形,二面角P-AD-B为120°. (1)求点P到平面ABCD的距离, (2)求二面角A-PB-C的余弦值
广东梅县东山中学高二理科数学中段考试答案
选择题:(本大题共8个小题,每小题5分,共40分)。
题号
1
2
3
4
5
6
7
8
答案
C
D
B
B
C
D
C
A
二、填空题:(本大题共6个小题,每小题5分,共30分)。
9、 12π 10、 11、___ x+2y+1=0_______
12、 1 13、 14、________________
三、解答题:
15.(本小题满分13分)21世纪教育网
(1)由题有所求直线与垂直,则可设直线的方程为 . ………3分
把点P(-2,2)的坐标代入得 ,即C=4. …………6分
∴所求直线的方程为. …………7分
(2)∵直线为
∴令,令;
则直线的方程知它在轴、轴上的截距分别是, ………11分
所以直线与两坐标轴围成三角形的面积. ………13分
16.(本小题满分13分)
…………2分
…………4分
(1)∵
∴ …………7分
解得 …………8分
(2)∵
∴ …………11分
解得 …………13分
17.(本小题满分14分)
解:(1)由正方形ABCD知,∠DCF=∠DAE=90°, …………2分 ∴ , …………4分 ∵ ∴. …………6分
∵,EF= ∴ ∴△A1EF的面积为 …………9分 ∵
∴A1D是三棱锥D-A1EF的底面A1EF上的高线, …………11分 因此,三棱锥A1-DEF的体积为:
…………14分
18.(本小题满分14分)
解法一:(向量法)
(1)建立以D为坐标原点的,DA,DC,DP分别为x轴,y轴,z轴的空间直角坐标系,如图所示。 …………1分
则P(0,0,1) , A(1,0,0) , C(0,1,0) , E(1,,0) , F(,1,0) , D(0,0,0)
=(,,)
=(1,,-1) …………2分
设平面PEF的法向量
则
令x=2,则y=2,z=3,所以, …………4分
又因为
所以点D到平面PEF的距离为
…………6分
因为,所以是平面EFB的法向量,
由(1)知,平面PEF的法向量为 …………7分
…………10分
(3)假设存在点M,当DM=(0<<1)时满足条件,则M(0,0,)
=(1,, -) 设=(x,y ,1)是平面MEF的一个法向量
∴
∴x=y= ∴ =(, ,1) …………12分
则 解得 =……13分
故存在点M,使DM=时,满足条件. …………14分
法二:(等体积法)连接DE,DF,EF=
因为,所以,且点P到平面DEF的距离为PD
因为ABCD是正方形,E,F是AB,BC的中点,所以DE=DF=
所以PE=PF=,
取EF的中点H,连接PH,DH,因为PE=PF,DE=DF所以PHEF;DHEF
……3分
…………5分
设点D到平面PEF的距离为h
………6分
因为PHEF;DHEF,所以为平面PEF与平面DEF所成的二面角…7分
…………9分
由题可知二面角P-EF-D与P-EF-B互补
所以二面角P-EH-B的余弦值为 …………10分
(3)过点D作DH⊥EF于H,连接MH
∵PD⊥平面ABCD ∴MH⊥EF
∴ ∠MHD就是二面角M-EF-D的平面角 …………11分
若∠MHD=30° 设DM=x(0在Rt△ADE中, ,
在Rt△MEH中,
在Rt△MDE中,
∴
∵0故存在点M,使DM=时,满足条件. …………14分
19.(本小题满分14分)
解:(1)设直线的斜率为(存在)则方程为. …………1分
又圆C的圆心为,半径,
由 , 解得. …………2分
所以直线方程为, 即 . …………3分
当的斜率不存在时,的方程为,经验证也满足条件. …………4分
综上:直线方程为:, …………5分
(2)由于,而弦心距,
所以. …………7分
所以为的中点.
故以为直径的圆的方程为. …………8分
(3)把直线即.代入圆的方程,
消去,整理得. …………9分
由于直线交圆于两点,
故,即,解得.
则实数的取值范围是. …………10分
设符合条件的实数存在,
由于垂直平分弦,故圆心必在上.
所以的斜率,而,所以. ………12分
由于,
故不存在实数,使得过点的直线垂直平分弦. ………14分
20.(本小题满分12分)21世纪教育网
解(1) ①当时,此时A点与D点重合, 折痕所在的直线方程 ……1分
②当时,将矩形折叠后A点落在线段CD上的点为G(a,1),
所以A与G关于折痕所在的直线对称,有……2分
故G点坐标为
从而折痕所在的直线与OG的交点坐标(线段OG的中点)为
折痕所在的直线方程,即 ……4分
由①、②得折痕所在的直线方程为:
k=0时,;时 …………5分
(2)⑴当时,折痕的长为2; …………6分
⑵当时,
①如下图,折痕所在的直线与
边AD、BC的交点坐标为
这时,, ……7分
②如下图,折痕所在的直线与边AD、AB的交点坐标为
这时,,
…………9分
③如下图,折痕所在的直线与边CD、AB的交点坐标为
这时,, ………11分
综上述,当时,折痕的长为2;
当时,折痕长
当时,折痕长
当时,折痕长 …………12分
高二理科数学试题
一、选择题:(8×5分=40分)
1.下列说法正确的是( )
A. 平行于同一平面的两条直线平行 B.与某一平面成等角的两条直线平行
C. 垂直于同一平面的两条直线平行 D.垂直于同一直线的两条直线平行
2.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( ).
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1
D.异面直线AD与CB1角为60°
3. 一个长方体,其正视图面积为,侧视图面积为,俯视图面积为,则长方体的对角线长为( )
A. B. C.6 D.
4.直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则( )
A.a=2,b=5; B.a=2,b=; C.a=,b=5; D.a=,b=
5.直线与直线3x+4y-15=0垂直,与圆相切,则直线的方程是( )
A.4x-3y-6=0 B.4x-3y-66=0
C.4x-3y-6=0或4x-3y-66=0 D.4x-3y-15=0
6. 已知,若三向量共面,则实数λ等于 ( )
A B C D
7.线段AB与x轴平行,且|AB|=5 , 若点A的坐标为(2,1) , 则点B的坐标为(??? )
A. (2,-3)或(2,7)?????? B. (2,-3)或(2,5)?????
C.(-3,1)或(7,1)?????? ? D.(-3,1)或(5,1)
8.异面直线a,b所成的角60°,直线a⊥c,则直线b与c所成的角的范围为( ).
A.[30°,90°] B.[60°,90°]
C.[30°,60°] D.[30°,120°]
二、填空题(6×5分=30分)
9. 若一个球的体积为,则它的表面积为________________
10. 直线被圆截得弦长为__________
11.过圆x2+y2-6x+4y-3=0的圆心,且平行于x+2y+11=0的直线方程是___________
?
12. 已知向量,满足,, 与的夹角为60°,则= __
13.如图2,在正三棱柱中,已知在棱上,且,若与平面所成的角为,则 .
14.在平面直角坐标系中,设三角形ABC 的顶点分别为A(0,a),B(b,0),C (c,0) ,点P(0,p)在线段AO 上(异于端点),设a,b,c, p 均为非零实数,直线BP,CP 分别交AC , AB 于点E ,F ,一同学已正确算的OE的方程:,请你求OF的方程: ____________________。
三、解答题:解答须写出文字说明、证明过程和演算步骤。
15.
16.已知直线经过直线与直线的交点,且垂直于直线.(1)求直线的方程;(2)求直线与两坐标轴围成的三角形的面积.
17. 如图,边长为1的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1. (1)求证:A1D⊥平面AEF; (2)求三棱锥A1-DEF的体积.
18.已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:
(1)平面ADE∥平面B1C1F;
(2)在AE上求一点M,使得A1M⊥平面DAE.
19.已知点及圆:.
(Ⅰ)若直线过点且与圆心的距离为1,求直线的方程;
(Ⅱ)设过P直线与圆交于、两点,当时,求以为直径的圆的方程;
(Ⅲ)设直线与圆交于,两点,是否存在实数,使得过点的直线垂直平分弦?若存在,求出实数的值;若不存在,请说明理由.
20.如图,已知四棱锥P-ABCD,PB⊥AD,△PAD是边长2的正三角形,底面ABCD为菱形,二面角P-AD-B为120°. (1)求点P到平面ABCD的距离, (2)求二面角A-PB-C的余弦值
广东梅县东山中学高二理科数学中段考试答案
选择题:(本大题共8个小题,每小题5分,共40分)。
题号
1
2
3
4
5
6
7
8
答案
C
D
B
B
C
D
C
A
二、填空题:(本大题共6个小题,每小题5分,共30分)。
9、 12π 10、 11、___ x+2y+1=0_______
12、 1 13、 14、________________
三、解答题:
15.(本小题满分13分)21世纪教育网
(1)由题有所求直线与垂直,则可设直线的方程为 . ………3分
把点P(-2,2)的坐标代入得 ,即C=4. …………6分
∴所求直线的方程为. …………7分
(2)∵直线为
∴令,令;
则直线的方程知它在轴、轴上的截距分别是, ………11分
所以直线与两坐标轴围成三角形的面积. ………13分
16.(本小题满分13分)
…………2分
…………4分
(1)∵
∴ …………7分
解得 …………8分
(2)∵
∴ …………11分
解得 …………13分
17.(本小题满分14分)
解:(1)由正方形ABCD知,∠DCF=∠DAE=90°, …………2分 ∴ , …………4分 ∵ ∴. …………6分
∵,EF= ∴ ∴△A1EF的面积为 …………9分 ∵
∴A1D是三棱锥D-A1EF的底面A1EF上的高线, …………11分 因此,三棱锥A1-DEF的体积为:
…………14分
18.(本小题满分14分)
解法一:(向量法)
(1)建立以D为坐标原点的,DA,DC,DP分别为x轴,y轴,z轴的空间直角坐标系,如图所示。 …………1分
则P(0,0,1) , A(1,0,0) , C(0,1,0) , E(1,,0) , F(,1,0) , D(0,0,0)
=(,,)
=(1,,-1) …………2分
设平面PEF的法向量
则
令x=2,则y=2,z=3,所以, …………4分
又因为
所以点D到平面PEF的距离为
…………6分
因为,所以是平面EFB的法向量,
由(1)知,平面PEF的法向量为 …………7分
…………10分
(3)假设存在点M,当DM=(0<<1)时满足条件,则M(0,0,)
=(1,, -) 设=(x,y ,1)是平面MEF的一个法向量
∴
∴x=y= ∴ =(, ,1) …………12分
则 解得 =……13分
故存在点M,使DM=时,满足条件. …………14分
法二:(等体积法)连接DE,DF,EF=
因为,所以,且点P到平面DEF的距离为PD
因为ABCD是正方形,E,F是AB,BC的中点,所以DE=DF=
所以PE=PF=,
取EF的中点H,连接PH,DH,因为PE=PF,DE=DF所以PHEF;DHEF
……3分
…………5分
设点D到平面PEF的距离为h
………6分
因为PHEF;DHEF,所以为平面PEF与平面DEF所成的二面角…7分
…………9分
由题可知二面角P-EF-D与P-EF-B互补
所以二面角P-EH-B的余弦值为 …………10分
(3)过点D作DH⊥EF于H,连接MH
∵PD⊥平面ABCD ∴MH⊥EF
∴ ∠MHD就是二面角M-EF-D的平面角 …………11分
若∠MHD=30° 设DM=x(0
在Rt△MEH中,
在Rt△MDE中,
∴
∵0
19.(本小题满分14分)
解:(1)设直线的斜率为(存在)则方程为. …………1分
又圆C的圆心为,半径,
由 , 解得. …………2分
所以直线方程为, 即 . …………3分
当的斜率不存在时,的方程为,经验证也满足条件. …………4分
综上:直线方程为:, …………5分
(2)由于,而弦心距,
所以. …………7分
所以为的中点.
故以为直径的圆的方程为. …………8分
(3)把直线即.代入圆的方程,
消去,整理得. …………9分
由于直线交圆于两点,
故,即,解得.
则实数的取值范围是. …………10分
设符合条件的实数存在,
由于垂直平分弦,故圆心必在上.
所以的斜率,而,所以. ………12分
由于,
故不存在实数,使得过点的直线垂直平分弦. ………14分
20.(本小题满分12分)21世纪教育网
解(1) ①当时,此时A点与D点重合, 折痕所在的直线方程 ……1分
②当时,将矩形折叠后A点落在线段CD上的点为G(a,1),
所以A与G关于折痕所在的直线对称,有……2分
故G点坐标为
从而折痕所在的直线与OG的交点坐标(线段OG的中点)为
折痕所在的直线方程,即 ……4分
由①、②得折痕所在的直线方程为:
k=0时,;时 …………5分
(2)⑴当时,折痕的长为2; …………6分
⑵当时,
①如下图,折痕所在的直线与
边AD、BC的交点坐标为
这时,, ……7分
②如下图,折痕所在的直线与边AD、AB的交点坐标为
这时,,
…………9分
③如下图,折痕所在的直线与边CD、AB的交点坐标为
这时,, ………11分
综上述,当时,折痕的长为2;
当时,折痕长
当时,折痕长
当时,折痕长 …………12分
同课章节目录
