2021-2022学年人教版数学八年级下册17.1勾股定理课件 (共13张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.1勾股定理课件 (共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 676.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:39:07 | ||
图片预览



文档简介
(共13张PPT)
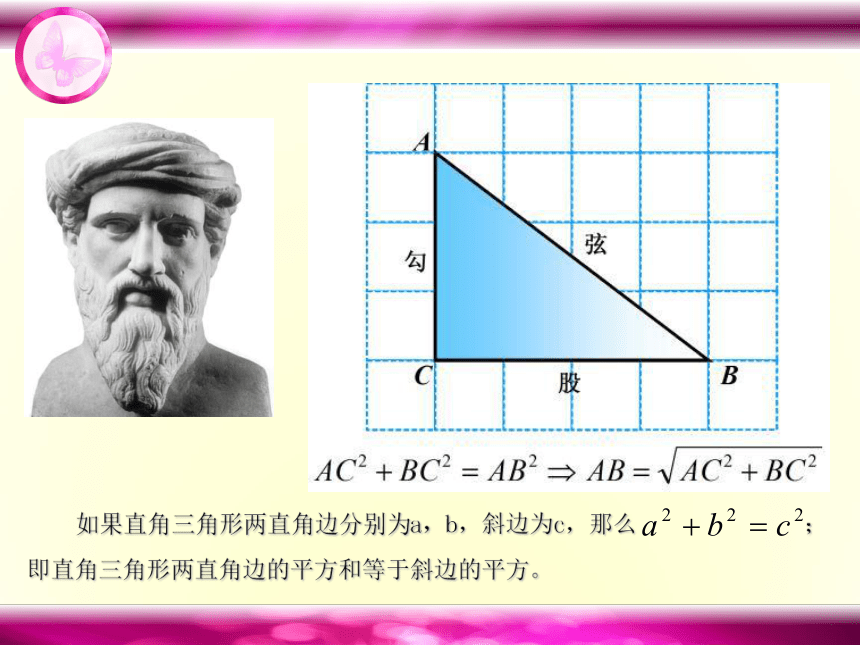
第十七章 勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么 ; 即直角三角形两直角边的平方和等于斜边的平方。
学习目标:
1、掌握勾股定理,理解勾股定理的证明过程。
2、能用勾股定理解决有关直角三角形的边的计算问题。
重难点:
通过勾股定理的探究过程,加深对数形 结合思想的认识。
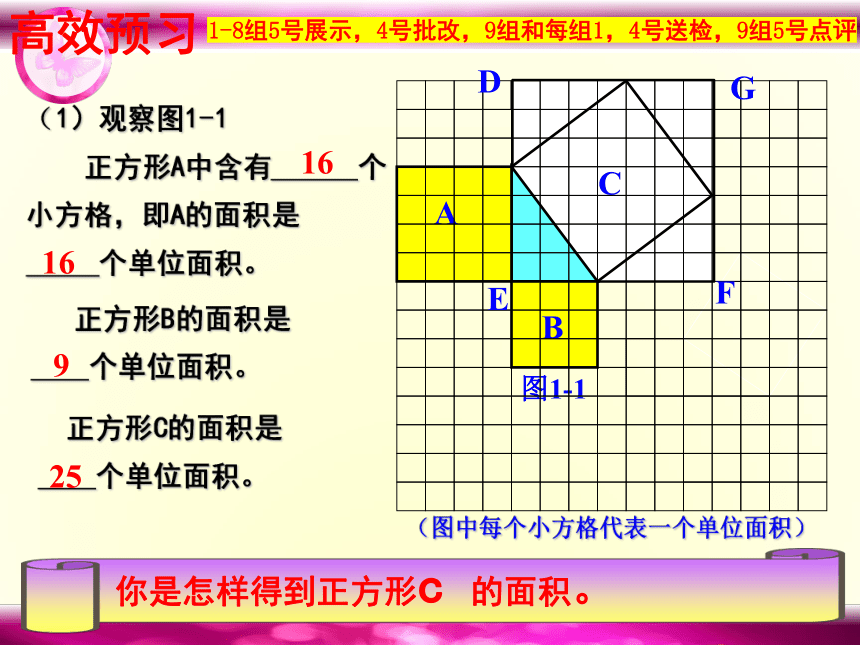
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
16
16
9
25
你是怎样得到正方形c 的面积。
A
B
C
图1-1
(图中每个小方格代表一个单位面积)
高效预习
D
G
E
F
1-8组5号展示,4号批改,9组和每组1,4号送检,9组5号点评
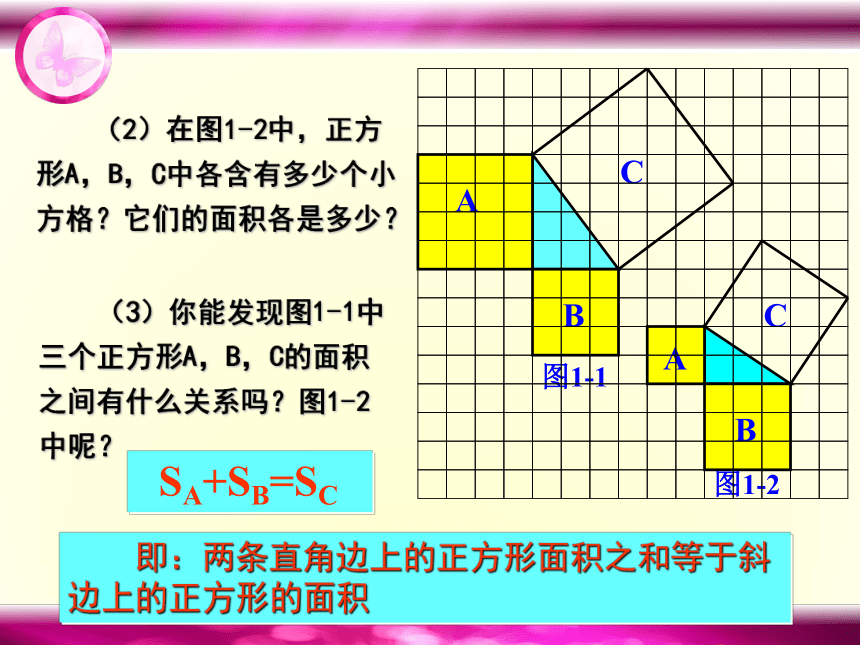
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
A
B
C
图1-1
A
B
C
图1-2
归纳:
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么____
c
a
b
c
a
b
c
a
b
c
a
b
证明:∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
如图,将4个全等的直角三角形拼成一个大的正方形,利用此图验证勾股定理。
小组研习1:勾股定理的证明
思路探究:
(1)拼得的大正方形的边长为
____ ,则它的面积是___ 。
(2)因为图形是拼接的,所以大正方形的面积还可以表示为
__+4 ×__ = __
1-8组3号展示,2号批改,9组和每组1,2号送检,9组3号点评
小组研习2:运用勾股定理计算求值
1-8组2号展示,1号批改,9组和每组1,3号送检,9组2号点评
1、《课时练》第16页例1、
规律方法
利用勾股定理可以解决两类问题:
(1)已知直角三角形的两边长,求第三边的长,
(2)已知直角三角形的一边长和另外两边的数量关系,求另外两边的长,
应用勾股定理需注意两点:
(1)只有在直角三角形中,才能应用勾股定理;
(2)直角三角形中已知的两边没有明确是直角边还是斜边时,必须分类讨论.
小组研习2:运用勾股定理计算求值
A
B
C
D
E
选做:如图,在△ABC中,CA=CB,AD ⊥BC,BE ⊥AC,AB=5,AD=4,则AE=___.
思路探究:(1)要求AE 的长,在Rt△ABE中,已知AB=5,只需求出___即可。
(2)BE与AD有什么样的数量关系?请给出证明。
1-8组1号展示,2号批改,9组和每组2,3号送检,9组2号点评
2、《课时练》第17页例2、
规律方法
斜三角形作高的“三准则”
在非直角三角形中求有关线段的长时,常需添加辅助线构造直角三角形,而构造直角三角形最常用的方法就是作三角形的某条高.作高时,有三个准则可以参考:
(1)求三角形的面积尽量作已知边上的高:
(2)如果已知角度,要利用30,45°,60°这三个特殊角构造直角三角形;
(3)如果已知边长,应把 3,4,5;6,8,10;5,12,13等这些常作为直角三角形的边长出现的整数值构造进直角三角形中,而不是分割“破坏”这些边长.
c
a
b
c
a
b
反馈练习
1、变式训练1、2、3、
3、若直角三角形的两直角边长分别为a,b,且满足 , 则该直角三角形斜边长为___。
选做4、.如图所示,用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理。
C
A
B
D
1-8组4号展示,3号批改,9组和每组1,3号送检,9组4号点评
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AEBC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
选做
第十七章 勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么 ; 即直角三角形两直角边的平方和等于斜边的平方。
学习目标:
1、掌握勾股定理,理解勾股定理的证明过程。
2、能用勾股定理解决有关直角三角形的边的计算问题。
重难点:
通过勾股定理的探究过程,加深对数形 结合思想的认识。
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
16
16
9
25
你是怎样得到正方形c 的面积。
A
B
C
图1-1
(图中每个小方格代表一个单位面积)
高效预习
D
G
E
F
1-8组5号展示,4号批改,9组和每组1,4号送检,9组5号点评
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
A
B
C
图1-1
A
B
C
图1-2
归纳:
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么____
c
a
b
c
a
b
c
a
b
c
a
b
证明:∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
如图,将4个全等的直角三角形拼成一个大的正方形,利用此图验证勾股定理。
小组研习1:勾股定理的证明
思路探究:
(1)拼得的大正方形的边长为
____ ,则它的面积是___ 。
(2)因为图形是拼接的,所以大正方形的面积还可以表示为
__+4 ×__ = __
1-8组3号展示,2号批改,9组和每组1,2号送检,9组3号点评
小组研习2:运用勾股定理计算求值
1-8组2号展示,1号批改,9组和每组1,3号送检,9组2号点评
1、《课时练》第16页例1、
规律方法
利用勾股定理可以解决两类问题:
(1)已知直角三角形的两边长,求第三边的长,
(2)已知直角三角形的一边长和另外两边的数量关系,求另外两边的长,
应用勾股定理需注意两点:
(1)只有在直角三角形中,才能应用勾股定理;
(2)直角三角形中已知的两边没有明确是直角边还是斜边时,必须分类讨论.
小组研习2:运用勾股定理计算求值
A
B
C
D
E
选做:如图,在△ABC中,CA=CB,AD ⊥BC,BE ⊥AC,AB=5,AD=4,则AE=___.
思路探究:(1)要求AE 的长,在Rt△ABE中,已知AB=5,只需求出___即可。
(2)BE与AD有什么样的数量关系?请给出证明。
1-8组1号展示,2号批改,9组和每组2,3号送检,9组2号点评
2、《课时练》第17页例2、
规律方法
斜三角形作高的“三准则”
在非直角三角形中求有关线段的长时,常需添加辅助线构造直角三角形,而构造直角三角形最常用的方法就是作三角形的某条高.作高时,有三个准则可以参考:
(1)求三角形的面积尽量作已知边上的高:
(2)如果已知角度,要利用30,45°,60°这三个特殊角构造直角三角形;
(3)如果已知边长,应把 3,4,5;6,8,10;5,12,13等这些常作为直角三角形的边长出现的整数值构造进直角三角形中,而不是分割“破坏”这些边长.
c
a
b
c
a
b
反馈练习
1、变式训练1、2、3、
3、若直角三角形的两直角边长分别为a,b,且满足 , 则该直角三角形斜边长为___。
选做4、.如图所示,用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理。
C
A
B
D
1-8组4号展示,3号批改,9组和每组1,3号送检,9组4号点评
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AEBC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
选做
