浙江省金华市义乌市绣湖中学2021-2022学年八年级下学期寒假作业监测(开学)数学试题(word版,含答案)
文档属性
| 名称 | 浙江省金华市义乌市绣湖中学2021-2022学年八年级下学期寒假作业监测(开学)数学试题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 332.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:02:33 | ||
图片预览


文档简介
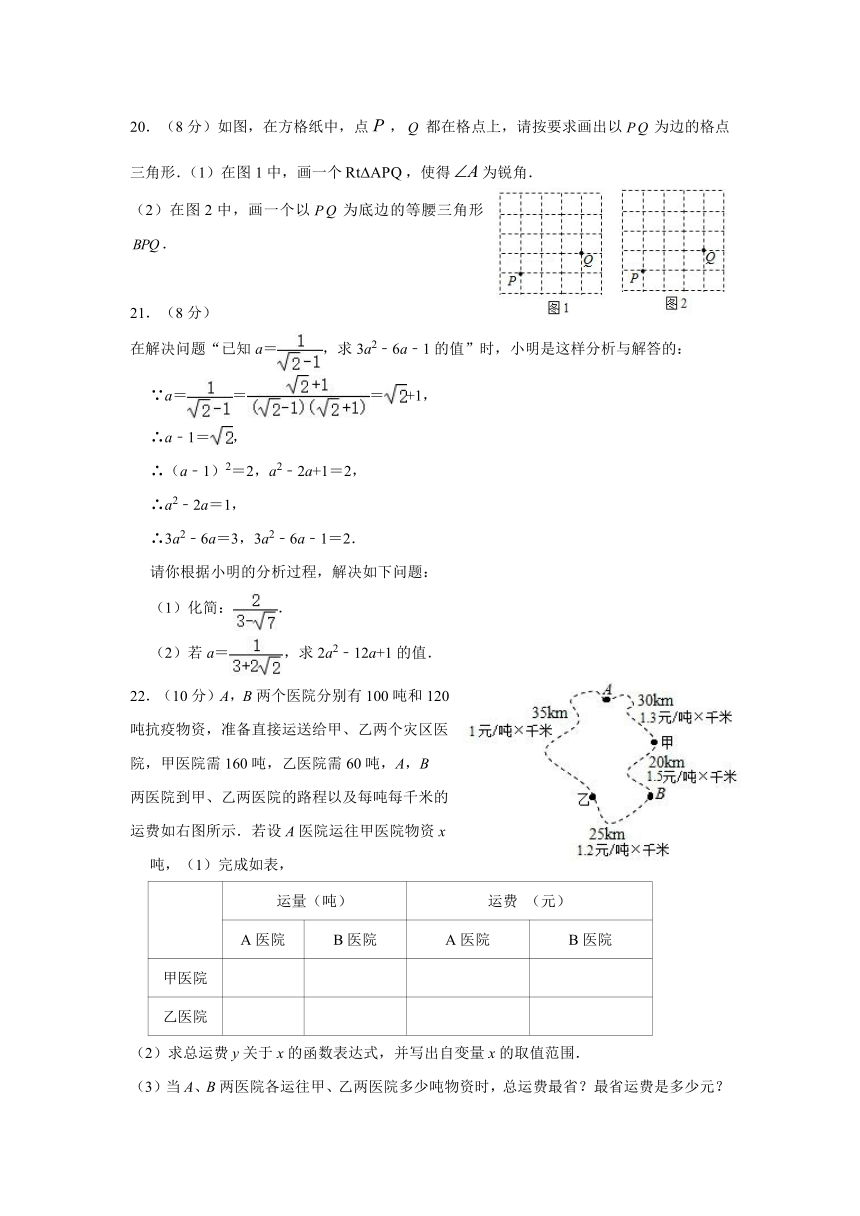
绣湖中学八年级数学学情调研卷2022.2.16
一、选择题(每小题3分,共30分)
1.下列长度的三条线段,能组成三角形的是( )
A.3,5,7 B.3,6,10 C.5,5,11 D.5,6,11
2.下列垃圾分类的图标(不含文字与字母部分)中,是轴对称图形的是
A. B. C. D.
3.如图,小明家相对于学校的位置,下列描述最正确的是( )
A.在距离学校300米处 B.在学校的北偏东320方向
C.在北偏东580方向300米处 D.在学校北偏东580方向300米处
4.若函数y=kx(k≠0)的图象过点P(﹣1,3),则该图象必过点( )
A.(1,3) B.(1,﹣3) C.(﹣3,1) D.(3,﹣1)
5.下列计算结果正确的是( )
A. B. C. D.
6.已知点P(2a+1,1﹣a)在第一象限,则a的取值范围在数轴上表示正确的是( )
A. B. C. D.
7. 对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )
A.∠1=50°,∠2=40° B.∠1=50°,∠2=50°
C.∠1=∠2=45° D.∠1=40°,∠2=40°
8.已知直线经过第一、二、三象限,且点在该直线上,设,则的取值范围是
A. B. C. D.
9.如图,某自动感应门的正上方处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生正对门,缓慢走到离门1.2米的地方时米),感应门自动打开,则人头顶离感应器的距离等于
A.1.2米 B.1.5米 C.2.0米 D.2.5米
10.在平面直角坐标系中,已知直线l1:y=-2x+4交y轴于点A,若l1关于y轴的对称直线为l2,
直线l2的有一个点M ,当M 点到直线l1的距离小于,则点M 的横坐标m取值范
围是( )
A.-2二、填空题(每小题3分,共18分)
11.若点P(2,-3)向左平移5个单位后点Q的坐标为 .
12.命题“若a,b互为倒数,则ab=1”的逆命题是 .
13.若分式有意义,则x的取值范围是 .
14.已知一次函数y=kx+k﹣1(其中k为常数且k≠0)的图像不经
过第二象限,则k的取值范围是 .
15.如图,在一张直角三角形纸片ABC中,∠ACB=90°,BC=1,AC=,
P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP,CA1交AB于点D.当△A1PD为直角三角形时,则AP的长度为____________。
16.如图,在平面直角坐标系xoy中,直线l:y= - x-2 交x轴于
点A,交y轴于点B,作点A关于y轴的对称点C,D是直线l
上的动点,连CD,将CD绕C点逆时针旋转900至CE。
则(1)点C的坐标是_______(2)OE+AE的最小值是_______.
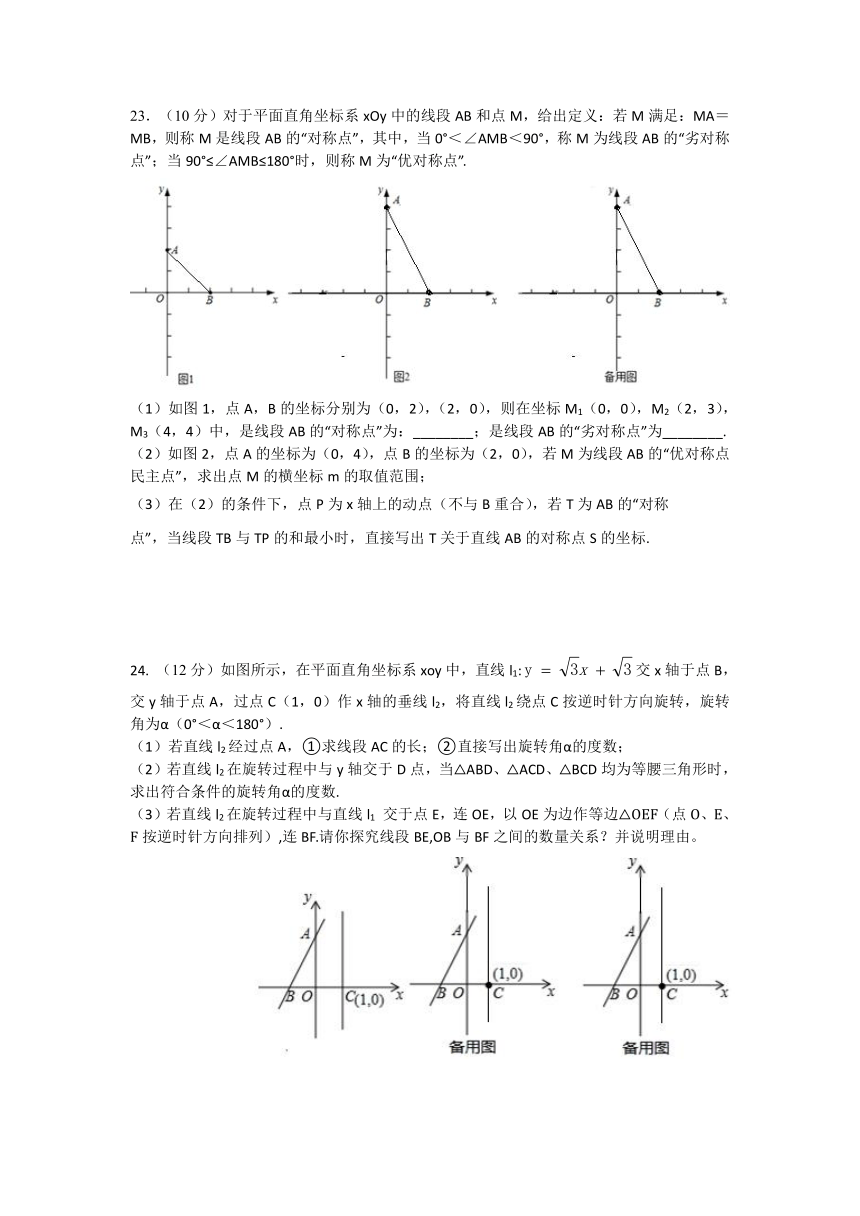
三、解答题(8大题,共66分)
17.(6分)解下列一元二次方程:
(1)(x﹣4)(x﹣5)=20; (2)x2﹣6x﹣1=0.
18.(6分)如图,DF∥AC,DF=AC,DA=EB.
求证:∠F=∠C.
19.(6分)已知点P(4-m,m-1).(1)若点在轴上,求的值.
(2)若点到x轴的距离是到y轴距离的2倍相等,求点的坐标.
20.(8分)如图,在方格纸中,点,都在格点上,请按要求画出以为边的格点三角形.(1)在图1中,画一个,使得为锐角.
(2)在图2中,画一个以为底边的等腰三角形.
21.(8分)
在解决问题“已知a=,求3a2﹣6a﹣1的值”时,小明是这样分析与解答的:
∵a===+1,
∴a﹣1=,
∴(a﹣1)2=2,a2﹣2a+1=2,
∴a2﹣2a=1,
∴3a2﹣6a=3,3a2﹣6a﹣1=2.
请你根据小明的分析过程,解决如下问题:
(1)化简:.
(2)若a=,求2a2﹣12a+1的值.
22.(10分)A,B两个医院分别有100吨和120
吨抗疫物资,准备直接运送给甲、乙两个灾区医
院,甲医院需160吨,乙医院需60吨,A,B
两医院到甲、乙两医院的路程以及每吨每千米的
运费如右图所示.若设A医院运往甲医院物资x吨,(1)完成如表,
运量(吨) 运费 (元)
A医院 B医院 A医院 B医院
甲医院
乙医院
(2)求总运费y关于x的函数表达式,并写出自变量x的取值范围.
(3)当A、B两医院各运往甲、乙两医院多少吨物资时,总运费最省?最省运费是多少元?
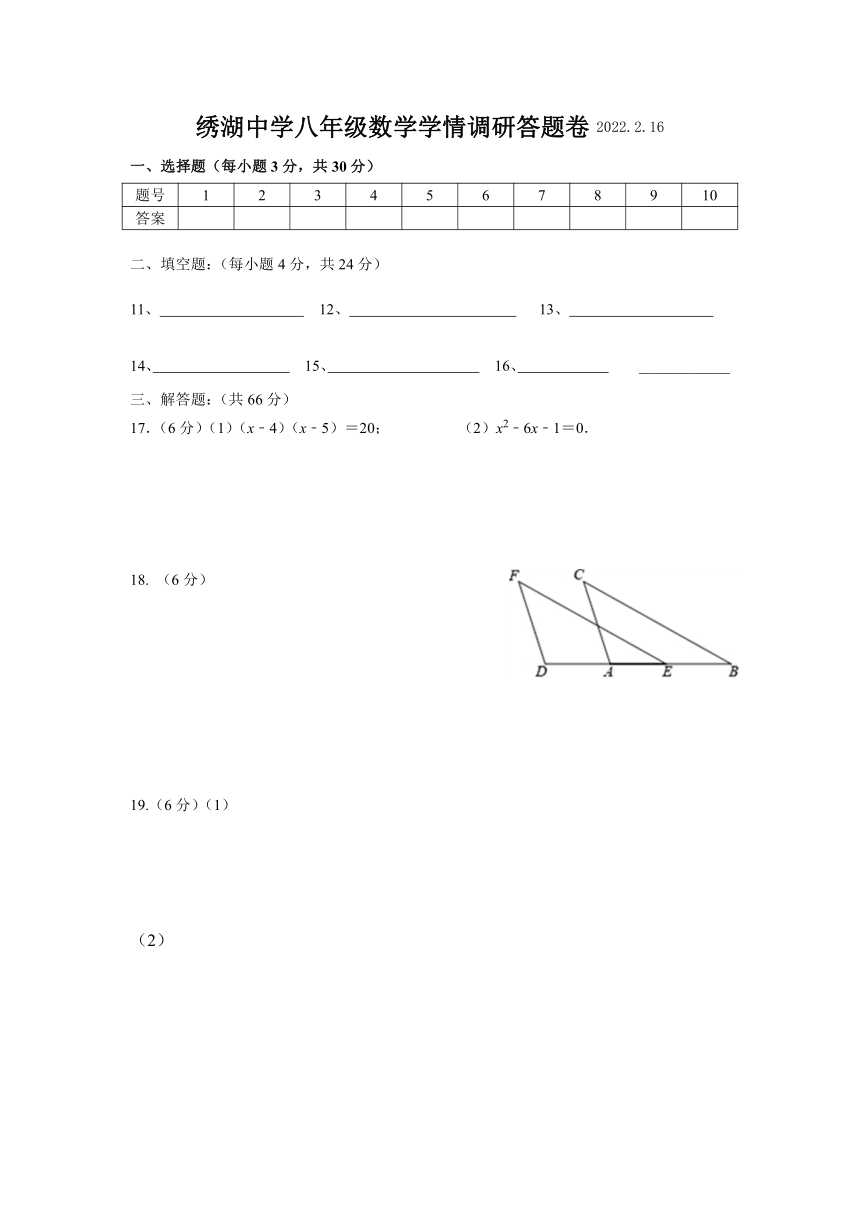
23.(10分)对于平面直角坐标系xOy中的线段AB和点M,给出定义:若M满足:MA=MB,则称M是线段AB的“对称点”,其中,当0°<∠AMB<90°,称M为线段AB的“劣对称点”;当90°≤∠AMB≤180°时,则称M为“优对称点”.
(1)如图1,点A,B的坐标分别为(0,2),(2,0),则在坐标M1(0,0),M2(2,3),M3(4,4)中,是线段AB的“对称点”为:________;是线段AB的“劣对称点”为________.
(2)如图2,点A的坐标为(0,4),点B的坐标为(2,0),若M为线段AB的“优对称点民主点”,求出点M的横坐标m的取值范围;
(3)在(2)的条件下,点P为x轴上的动点(不与B重合),若T为AB的“对称
点”,当线段TB与TP的和最小时,直接写出T关于直线AB的对称点S的坐标.
24. (12分)如图所示,在平面直角坐标系xoy中,直线l1:交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l2,将直线l2绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
(1)若直线l2经过点A,①求线段AC的长;②直接写出旋转角α的度数;
(2)若直线l2在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,求出符合条件的旋转角α的度数.
(3)若直线l2在旋转过程中与直线l1 交于点E,连OE,以OE为边作等边△OEF(点O、E、F按逆时针方向排列),连BF.请你探究线段BE,OB与BF之间的数量关系?并说明理由。
绣湖中学八年级数学学情调研答题卷2022.2.16
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:(每小题4分,共24分)
11、 12、 13、
14、 15、 16、 ____________
三、解答题:(共66分)
17.(6分)(1)(x﹣4)(x﹣5)=20; (2)x2﹣6x﹣1=0.
18. (6分)
19.(6分)(1)
(2)
20.(8分)(1)
(2)
(8分)(1)
(2)
22.(10分)(1)
运量(吨) 运费 (元)
A医院 B医院 A医院 B医院
甲医院
乙医院
(2)
(3)
23.(10分)
(1)①________________,___________________
(2)
(3)
24.(12分)
(1) ①
②
(2)
参考答案与评分标准
1、A 2、B 3、D 4、B 5、D 6、C 7、A 8、C 9、B 10、D
11、(-3,-3) 12、若ab=1,则a,b互为倒数。 13、x≥﹣3且x≠2 14、015、1或 16、(1)(2,0)(2)10
17、(1)x1=0,x2=9;(2)x1=3+,x2=3﹣.
18、略
19、(1)m=1(2分)(2)(1,2)和(-3,6)(4分) 20、略
21、(1)3+;(4分)(2)﹣1(4分)
22、(1)略 (4分)(2)y=4x+7100(2分)40x100(1分)(3)A运往甲40吨,运往乙60吨;B运往甲120吨,运往乙0吨;(2分)最省7260吨(1分)23、(1)M1 , M3;M3 (4分)(2)-1m3(4分)(3)S(2,2.5)(2分)
24、(1) ①AC= ,② α=30°(4分)
(2) (4分)∵OD垂直平分BC,∴DB=DC,
∴△DBC总是等腰三角形;
①当AD=AC=AB且D在A点上方时(图2),
∴∠ACD=∠ADC=15° ∵CE∥OD,
∴α=∠ODC=15°
②当DA=DC=DB时(图3),易知∠DAC=∠DCA=30°,
∴α=60°,
③当AD=AC=AB且D在A点下方时(图4),
易知∠ABD=∠ADB=∠ADC=∠ACD=75°,
∠DBC=∠DCB=15°,
∴α=105°;
④当AB=BD=DC=AC(图5)易知△BDC是等边三角形,
∴α=150°
综上所述:当α=15°或60°或105°或150°时,△ABD、△ACD、△BCD均为等腰三角形.
(2)当E在x轴上方时,BE=BO+BF
当E在x轴下方时,BE=BF-BO(4分)
一、选择题(每小题3分,共30分)
1.下列长度的三条线段,能组成三角形的是( )
A.3,5,7 B.3,6,10 C.5,5,11 D.5,6,11
2.下列垃圾分类的图标(不含文字与字母部分)中,是轴对称图形的是
A. B. C. D.
3.如图,小明家相对于学校的位置,下列描述最正确的是( )
A.在距离学校300米处 B.在学校的北偏东320方向
C.在北偏东580方向300米处 D.在学校北偏东580方向300米处
4.若函数y=kx(k≠0)的图象过点P(﹣1,3),则该图象必过点( )
A.(1,3) B.(1,﹣3) C.(﹣3,1) D.(3,﹣1)
5.下列计算结果正确的是( )
A. B. C. D.
6.已知点P(2a+1,1﹣a)在第一象限,则a的取值范围在数轴上表示正确的是( )
A. B. C. D.
7. 对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )
A.∠1=50°,∠2=40° B.∠1=50°,∠2=50°
C.∠1=∠2=45° D.∠1=40°,∠2=40°
8.已知直线经过第一、二、三象限,且点在该直线上,设,则的取值范围是
A. B. C. D.
9.如图,某自动感应门的正上方处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生正对门,缓慢走到离门1.2米的地方时米),感应门自动打开,则人头顶离感应器的距离等于
A.1.2米 B.1.5米 C.2.0米 D.2.5米
10.在平面直角坐标系中,已知直线l1:y=-2x+4交y轴于点A,若l1关于y轴的对称直线为l2,
直线l2的有一个点M ,当M 点到直线l1的距离小于,则点M 的横坐标m取值范
围是( )
A.-2
11.若点P(2,-3)向左平移5个单位后点Q的坐标为 .
12.命题“若a,b互为倒数,则ab=1”的逆命题是 .
13.若分式有意义,则x的取值范围是 .
14.已知一次函数y=kx+k﹣1(其中k为常数且k≠0)的图像不经
过第二象限,则k的取值范围是 .
15.如图,在一张直角三角形纸片ABC中,∠ACB=90°,BC=1,AC=,
P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP,CA1交AB于点D.当△A1PD为直角三角形时,则AP的长度为____________。
16.如图,在平面直角坐标系xoy中,直线l:y= - x-2 交x轴于
点A,交y轴于点B,作点A关于y轴的对称点C,D是直线l
上的动点,连CD,将CD绕C点逆时针旋转900至CE。
则(1)点C的坐标是_______(2)OE+AE的最小值是_______.
三、解答题(8大题,共66分)
17.(6分)解下列一元二次方程:
(1)(x﹣4)(x﹣5)=20; (2)x2﹣6x﹣1=0.
18.(6分)如图,DF∥AC,DF=AC,DA=EB.
求证:∠F=∠C.
19.(6分)已知点P(4-m,m-1).(1)若点在轴上,求的值.
(2)若点到x轴的距离是到y轴距离的2倍相等,求点的坐标.
20.(8分)如图,在方格纸中,点,都在格点上,请按要求画出以为边的格点三角形.(1)在图1中,画一个,使得为锐角.
(2)在图2中,画一个以为底边的等腰三角形.
21.(8分)
在解决问题“已知a=,求3a2﹣6a﹣1的值”时,小明是这样分析与解答的:
∵a===+1,
∴a﹣1=,
∴(a﹣1)2=2,a2﹣2a+1=2,
∴a2﹣2a=1,
∴3a2﹣6a=3,3a2﹣6a﹣1=2.
请你根据小明的分析过程,解决如下问题:
(1)化简:.
(2)若a=,求2a2﹣12a+1的值.
22.(10分)A,B两个医院分别有100吨和120
吨抗疫物资,准备直接运送给甲、乙两个灾区医
院,甲医院需160吨,乙医院需60吨,A,B
两医院到甲、乙两医院的路程以及每吨每千米的
运费如右图所示.若设A医院运往甲医院物资x吨,(1)完成如表,
运量(吨) 运费 (元)
A医院 B医院 A医院 B医院
甲医院
乙医院
(2)求总运费y关于x的函数表达式,并写出自变量x的取值范围.
(3)当A、B两医院各运往甲、乙两医院多少吨物资时,总运费最省?最省运费是多少元?
23.(10分)对于平面直角坐标系xOy中的线段AB和点M,给出定义:若M满足:MA=MB,则称M是线段AB的“对称点”,其中,当0°<∠AMB<90°,称M为线段AB的“劣对称点”;当90°≤∠AMB≤180°时,则称M为“优对称点”.
(1)如图1,点A,B的坐标分别为(0,2),(2,0),则在坐标M1(0,0),M2(2,3),M3(4,4)中,是线段AB的“对称点”为:________;是线段AB的“劣对称点”为________.
(2)如图2,点A的坐标为(0,4),点B的坐标为(2,0),若M为线段AB的“优对称点民主点”,求出点M的横坐标m的取值范围;
(3)在(2)的条件下,点P为x轴上的动点(不与B重合),若T为AB的“对称
点”,当线段TB与TP的和最小时,直接写出T关于直线AB的对称点S的坐标.
24. (12分)如图所示,在平面直角坐标系xoy中,直线l1:交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l2,将直线l2绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
(1)若直线l2经过点A,①求线段AC的长;②直接写出旋转角α的度数;
(2)若直线l2在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,求出符合条件的旋转角α的度数.
(3)若直线l2在旋转过程中与直线l1 交于点E,连OE,以OE为边作等边△OEF(点O、E、F按逆时针方向排列),连BF.请你探究线段BE,OB与BF之间的数量关系?并说明理由。
绣湖中学八年级数学学情调研答题卷2022.2.16
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:(每小题4分,共24分)
11、 12、 13、
14、 15、 16、 ____________
三、解答题:(共66分)
17.(6分)(1)(x﹣4)(x﹣5)=20; (2)x2﹣6x﹣1=0.
18. (6分)
19.(6分)(1)
(2)
20.(8分)(1)
(2)
(8分)(1)
(2)
22.(10分)(1)
运量(吨) 运费 (元)
A医院 B医院 A医院 B医院
甲医院
乙医院
(2)
(3)
23.(10分)
(1)①________________,___________________
(2)
(3)
24.(12分)
(1) ①
②
(2)
参考答案与评分标准
1、A 2、B 3、D 4、B 5、D 6、C 7、A 8、C 9、B 10、D
11、(-3,-3) 12、若ab=1,则a,b互为倒数。 13、x≥﹣3且x≠2 14、0
17、(1)x1=0,x2=9;(2)x1=3+,x2=3﹣.
18、略
19、(1)m=1(2分)(2)(1,2)和(-3,6)(4分) 20、略
21、(1)3+;(4分)(2)﹣1(4分)
22、(1)略 (4分)(2)y=4x+7100(2分)40x100(1分)(3)A运往甲40吨,运往乙60吨;B运往甲120吨,运往乙0吨;(2分)最省7260吨(1分)23、(1)M1 , M3;M3 (4分)(2)-1m3(4分)(3)S(2,2.5)(2分)
24、(1) ①AC= ,② α=30°(4分)
(2) (4分)∵OD垂直平分BC,∴DB=DC,
∴△DBC总是等腰三角形;
①当AD=AC=AB且D在A点上方时(图2),
∴∠ACD=∠ADC=15° ∵CE∥OD,
∴α=∠ODC=15°
②当DA=DC=DB时(图3),易知∠DAC=∠DCA=30°,
∴α=60°,
③当AD=AC=AB且D在A点下方时(图4),
易知∠ABD=∠ADB=∠ADC=∠ACD=75°,
∠DBC=∠DCB=15°,
∴α=105°;
④当AB=BD=DC=AC(图5)易知△BDC是等边三角形,
∴α=150°
综上所述:当α=15°或60°或105°或150°时,△ABD、△ACD、△BCD均为等腰三角形.
(2)当E在x轴上方时,BE=BO+BF
当E在x轴下方时,BE=BF-BO(4分)
同课章节目录
