2021—2022学年人教版八年级数学下册18.2.1矩形练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.1矩形练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 179.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:17:29 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学下册 第十八章平行四边形 18.2.1矩形 练习题
一、选择题
1.平行四边形和矩形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
2.下列说法不正确的是( )
A.有一个角为直角的平行四边形是矩形 B.有三个角为直角的四边形是矩形
C.对角线相等的平行四边形是矩形 D.对角线互相垂直的平行四边形是矩形
3.在平行四边形ABCD中,对角线AC、BD交于O点,下列条件中不能判定平行四边形ABCD是矩形的是( )
A.AC=BD B.AB⊥BC
C.OA=OB=OC=OD D.AC⊥BD
4.如图,矩形ABCD中,连接AC,延长BC至点E,使BE=AC,连接DE.若∠E=65°,则∠BAC的度数是( )
A.40° B.50° C.60° D.65°
5.如图,O是矩形ABCD的对角线的交点,M是AD的中点.若BC=8,OB=5,则OM的长为( )
A.2 B.2.5 C.3 D.4
6.四边形不具有稳定性,如图,矩形ABCD当改变内角大小就变成平行四边形ABC'D',若∠D'AB=30°,则平行四边形ABC'D'的面积与矩形ABCD的面积之比是( )
A. B. C. D.1
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( )
A.75° B.63° C.55° D.45°
9.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A、C的坐标分别是,,点B在第一象限,则点B的坐标是( )
A. B. C. D.
10.如图,□ABCD中,O是对角线AC、BD的交点,△ABO是等边三角形,若AC=8cm,则平行四边形ABCD的面积是( )cm2 .
A.16 B.4 C.8 D.16
二、填空题
11.矩形ABCD的对角线AC和BD相交于点O,∠ACB=40°,则∠AOB=_________°.
12.若矩形ABCD的周长为26cm,对角线的长是cm,则它的面积是_________.
13.如图,在四边形中,,,若再添加一个条件,就能推出四边形是矩形,你所添加的条件是______.(写出一种情况即可).
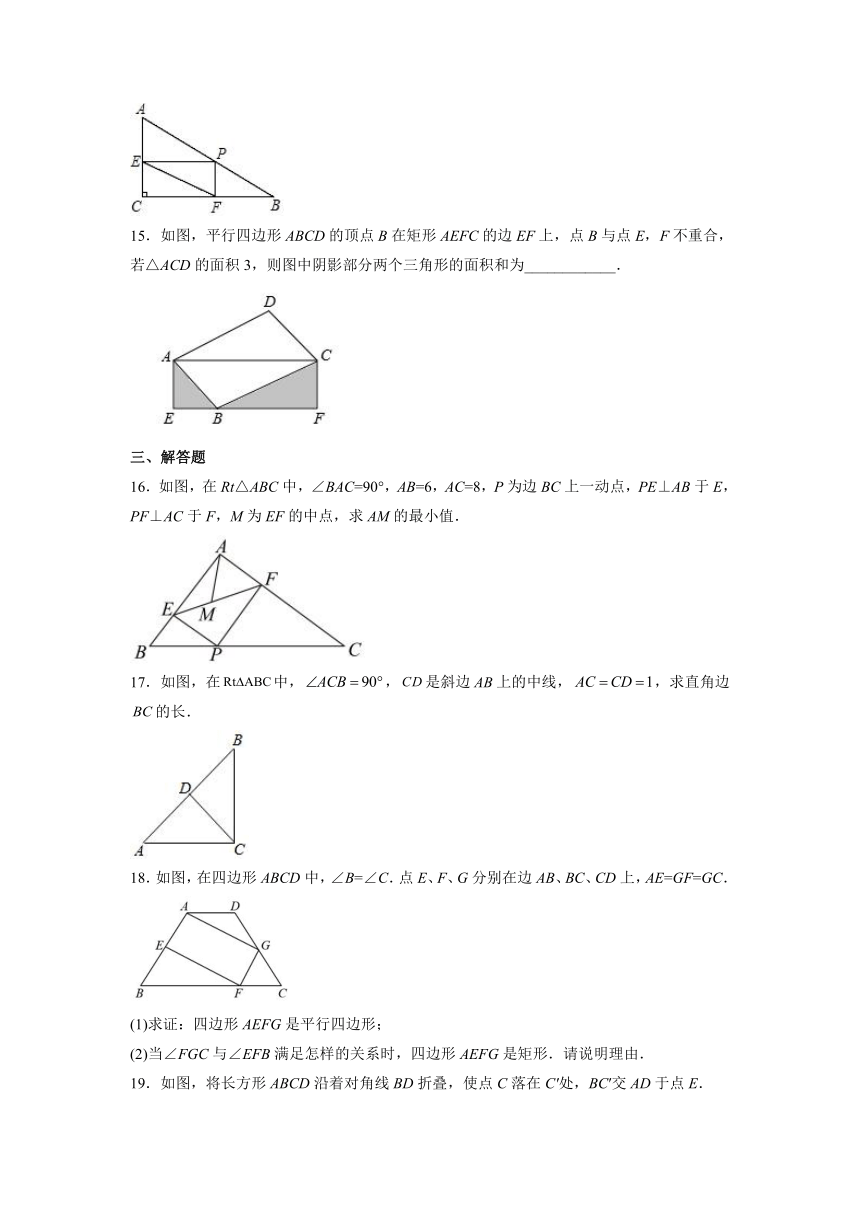
14.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是_________________.
15.如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积3,则图中阴影部分两个三角形的面积和为____________.
三、解答题
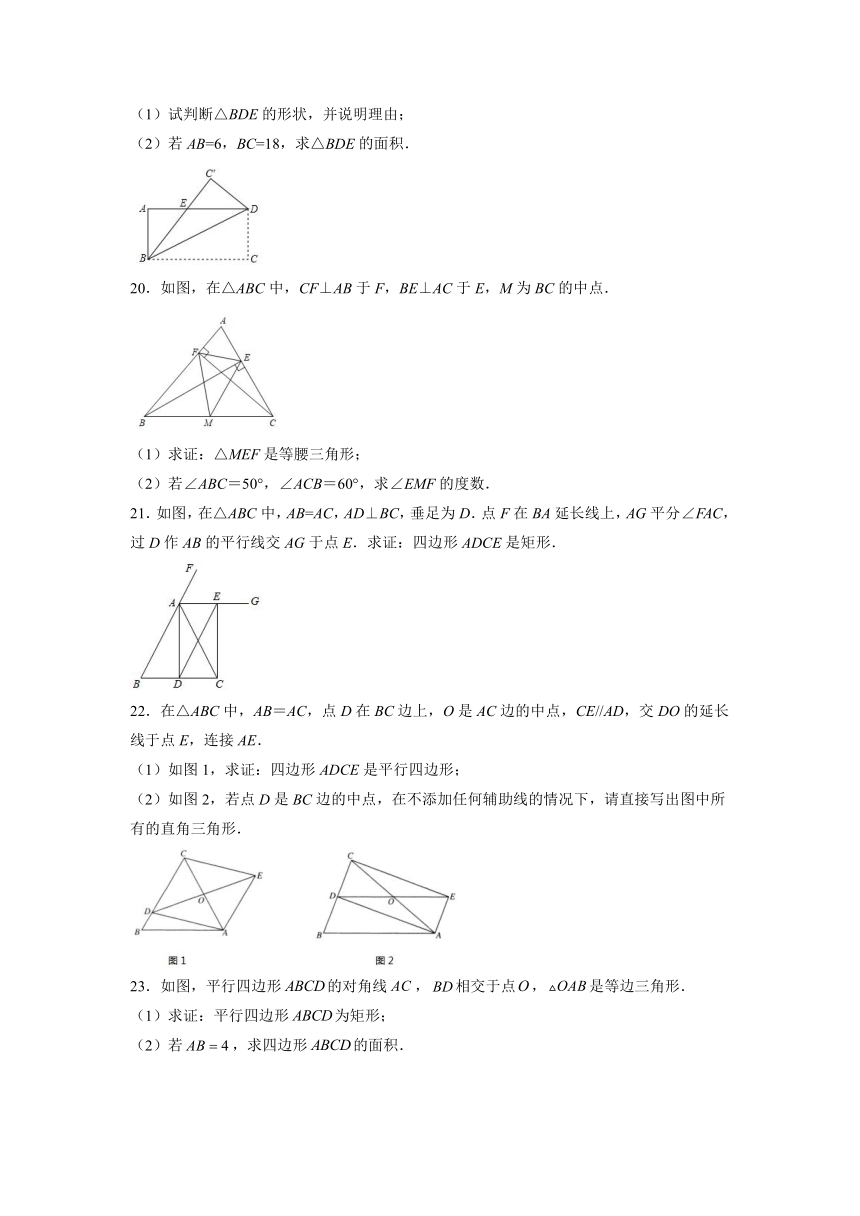
16.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,求AM的最小值.
17.如图,在中,,是斜边上的中线,,求直角边的长.
18.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.
19.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,BC=18,求△BDE的面积.
20.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)求证:△MEF是等腰三角形;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
21.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.点F在BA延长线上,AG平分∠FAC,过D作AB的平行线交AG于点E.求证:四边形ADCE是矩形.
22.在△ABC中,AB=AC,点D在BC边上,O是AC边的中点,CE//AD,交DO的延长线于点E,连接AE.
(1)如图1,求证:四边形ADCE是平行四边形;
(2)如图2,若点D是BC边的中点,在不添加任何辅助线的情况下,请直接写出图中所有的直角三角形.
23.如图,平行四边形的对角线,相交于点,是等边三角形.
(1)求证:平行四边形为矩形;
(2)若,求四边形的面积.
【参考答案】
1.A 2.D 3.D 4.A 5.C 6.A 7.A 8.A 9.B 10.D
11.80
12.20cm
13.或或(写出一种情况即可)
14.
15.3
16.解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP,EF与AP互相平分,
∵M是EF的中点,
∴M为AP的中点,
∴AM=AP,
∵AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,AP==4.8,
∴AP最短时,AP=4.8,
∴当AM最短时,AM=AP=2.4.
即AM的最小值为2.4.
17.解:在Rt△ABC中,CD是斜边AB上的中线,
∴AB=2CD=2,
由勾股定理得,BC= .
18(1)证明:在四边形ABCD中,∠B=∠C,
∵GF=GC,
∴∠C=∠GFC,∠B=∠GFC,
∴AB∥GF,即AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形.
(2)
解:当∠FGC=2∠EFB时,四边形AEFG是矩形;
∵∠FGC+∠GFC+∠C=180°,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
19.解:(1)△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形;
(2)设DE=x,则BE=x,AE=18﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即62+(18﹣x)2=x2,
解得:x=10,
所以S△BDE=DE×AB=×10×6=30.
20.(1)证明:∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=BC,FM=BC,
∴BM=FM,
∴△MEF是等腰三角形;
(2)∵BM=FM,∠ABC=50°,
∴∠MBF=∠MFB=50°,
∴∠BMF=180°﹣2×50°=80°,
∵CM=EM,∠ACB=60°,
∴∠MCE=∠MEC=60°,
∴∠CME=180°﹣2×60°=60°,
∴∠EMF=180°﹣∠BMF﹣∠CME=40°.
21.证明:∵AB=AC,
∴∠B=∠ACB,
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AEBD,AE=BD,
∵AD⊥BC,AB=AC,
∴BD=DC,
∴AEDC,AE=DC,
故四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
即四边形ADCE是矩形.
22.解:(1)∵CE//AD,
∴∠CED=∠ADE,
∵O是AC边的中点,
∴OA=OC,
∴在△COE和△AOD中,
,
∴△COE≌△AOD(AAS),
∴CE=AD,
又∵CE//AD,
∴四边形ADCE是平行四边形;
(2)∵点D是BC边的中点,
∴DC=DB,
又由(1)可知四边形ADCE是平行四边形,
∴DC=AE,DCAE,
∴DB=AE,
又∵DBAE,
∴四边形DBAE是平行四边形,
∴AB=DE,
又∵AB=AC,
∴DE=AC,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形,
∴∠DCE=∠CEA=∠EAD=∠ADC=90°,
∴∠BDA=90°,
∴直接三角形有:.
23.解:(1)证明: 为等边三角形,∴OA=OB
四边形是平行四边形
∴OA=OC,OB=OD
∴OA=OB=OC=OD
∴BD=AC
平行四边形为矩形
(2)由(1)知中,,
矩形的面积
一、选择题
1.平行四边形和矩形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
2.下列说法不正确的是( )
A.有一个角为直角的平行四边形是矩形 B.有三个角为直角的四边形是矩形
C.对角线相等的平行四边形是矩形 D.对角线互相垂直的平行四边形是矩形
3.在平行四边形ABCD中,对角线AC、BD交于O点,下列条件中不能判定平行四边形ABCD是矩形的是( )
A.AC=BD B.AB⊥BC
C.OA=OB=OC=OD D.AC⊥BD
4.如图,矩形ABCD中,连接AC,延长BC至点E,使BE=AC,连接DE.若∠E=65°,则∠BAC的度数是( )
A.40° B.50° C.60° D.65°
5.如图,O是矩形ABCD的对角线的交点,M是AD的中点.若BC=8,OB=5,则OM的长为( )
A.2 B.2.5 C.3 D.4
6.四边形不具有稳定性,如图,矩形ABCD当改变内角大小就变成平行四边形ABC'D',若∠D'AB=30°,则平行四边形ABC'D'的面积与矩形ABCD的面积之比是( )
A. B. C. D.1
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( )
A.75° B.63° C.55° D.45°
9.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A、C的坐标分别是,,点B在第一象限,则点B的坐标是( )
A. B. C. D.
10.如图,□ABCD中,O是对角线AC、BD的交点,△ABO是等边三角形,若AC=8cm,则平行四边形ABCD的面积是( )cm2 .
A.16 B.4 C.8 D.16
二、填空题
11.矩形ABCD的对角线AC和BD相交于点O,∠ACB=40°,则∠AOB=_________°.
12.若矩形ABCD的周长为26cm,对角线的长是cm,则它的面积是_________.
13.如图,在四边形中,,,若再添加一个条件,就能推出四边形是矩形,你所添加的条件是______.(写出一种情况即可).
14.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是_________________.
15.如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积3,则图中阴影部分两个三角形的面积和为____________.
三、解答题
16.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,求AM的最小值.
17.如图,在中,,是斜边上的中线,,求直角边的长.
18.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.
19.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,BC=18,求△BDE的面积.
20.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)求证:△MEF是等腰三角形;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
21.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.点F在BA延长线上,AG平分∠FAC,过D作AB的平行线交AG于点E.求证:四边形ADCE是矩形.
22.在△ABC中,AB=AC,点D在BC边上,O是AC边的中点,CE//AD,交DO的延长线于点E,连接AE.
(1)如图1,求证:四边形ADCE是平行四边形;
(2)如图2,若点D是BC边的中点,在不添加任何辅助线的情况下,请直接写出图中所有的直角三角形.
23.如图,平行四边形的对角线,相交于点,是等边三角形.
(1)求证:平行四边形为矩形;
(2)若,求四边形的面积.
【参考答案】
1.A 2.D 3.D 4.A 5.C 6.A 7.A 8.A 9.B 10.D
11.80
12.20cm
13.或或(写出一种情况即可)
14.
15.3
16.解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP,EF与AP互相平分,
∵M是EF的中点,
∴M为AP的中点,
∴AM=AP,
∵AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,AP==4.8,
∴AP最短时,AP=4.8,
∴当AM最短时,AM=AP=2.4.
即AM的最小值为2.4.
17.解:在Rt△ABC中,CD是斜边AB上的中线,
∴AB=2CD=2,
由勾股定理得,BC= .
18(1)证明:在四边形ABCD中,∠B=∠C,
∵GF=GC,
∴∠C=∠GFC,∠B=∠GFC,
∴AB∥GF,即AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形.
(2)
解:当∠FGC=2∠EFB时,四边形AEFG是矩形;
∵∠FGC+∠GFC+∠C=180°,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
19.解:(1)△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形;
(2)设DE=x,则BE=x,AE=18﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即62+(18﹣x)2=x2,
解得:x=10,
所以S△BDE=DE×AB=×10×6=30.
20.(1)证明:∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=BC,FM=BC,
∴BM=FM,
∴△MEF是等腰三角形;
(2)∵BM=FM,∠ABC=50°,
∴∠MBF=∠MFB=50°,
∴∠BMF=180°﹣2×50°=80°,
∵CM=EM,∠ACB=60°,
∴∠MCE=∠MEC=60°,
∴∠CME=180°﹣2×60°=60°,
∴∠EMF=180°﹣∠BMF﹣∠CME=40°.
21.证明:∵AB=AC,
∴∠B=∠ACB,
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AEBD,AE=BD,
∵AD⊥BC,AB=AC,
∴BD=DC,
∴AEDC,AE=DC,
故四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
即四边形ADCE是矩形.
22.解:(1)∵CE//AD,
∴∠CED=∠ADE,
∵O是AC边的中点,
∴OA=OC,
∴在△COE和△AOD中,
,
∴△COE≌△AOD(AAS),
∴CE=AD,
又∵CE//AD,
∴四边形ADCE是平行四边形;
(2)∵点D是BC边的中点,
∴DC=DB,
又由(1)可知四边形ADCE是平行四边形,
∴DC=AE,DCAE,
∴DB=AE,
又∵DBAE,
∴四边形DBAE是平行四边形,
∴AB=DE,
又∵AB=AC,
∴DE=AC,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形,
∴∠DCE=∠CEA=∠EAD=∠ADC=90°,
∴∠BDA=90°,
∴直接三角形有:.
23.解:(1)证明: 为等边三角形,∴OA=OB
四边形是平行四边形
∴OA=OC,OB=OD
∴OA=OB=OC=OD
∴BD=AC
平行四边形为矩形
(2)由(1)知中,,
矩形的面积
