2021-2022学年苏科版七年级数学下册7.2探索平行线的性质同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.2探索平行线的性质同步达标测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:21:12 | ||
图片预览


文档简介
2021-2022学年苏科版七年级数学下册《7-2探索平行线的性质》同步达标测试题(附答案)
一.选择题(共9小题,满分45分)
1.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于( )
A.116° B.118° C.120° D.124°
2.一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FD∥AB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
3.如图,AB∥CD,AD⊥CE于点A,∠1=60°,则∠2的度数是( )
A.30° B.40° C.45° D.60°
4.如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2 B.∠2=2∠1 C.180°﹣∠1﹣∠2 D.180°﹣∠2+∠1
5.如图,AB∥EF,∠C=90°,则α、β和γ的关系是( )
A.β=α+γ B.α+β+γ=180° C.α+β﹣γ=90° D.β+γ﹣α=180°
6.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.42°、138° B.都是10°
C.42°、138°或10°、10° D.以上都不对
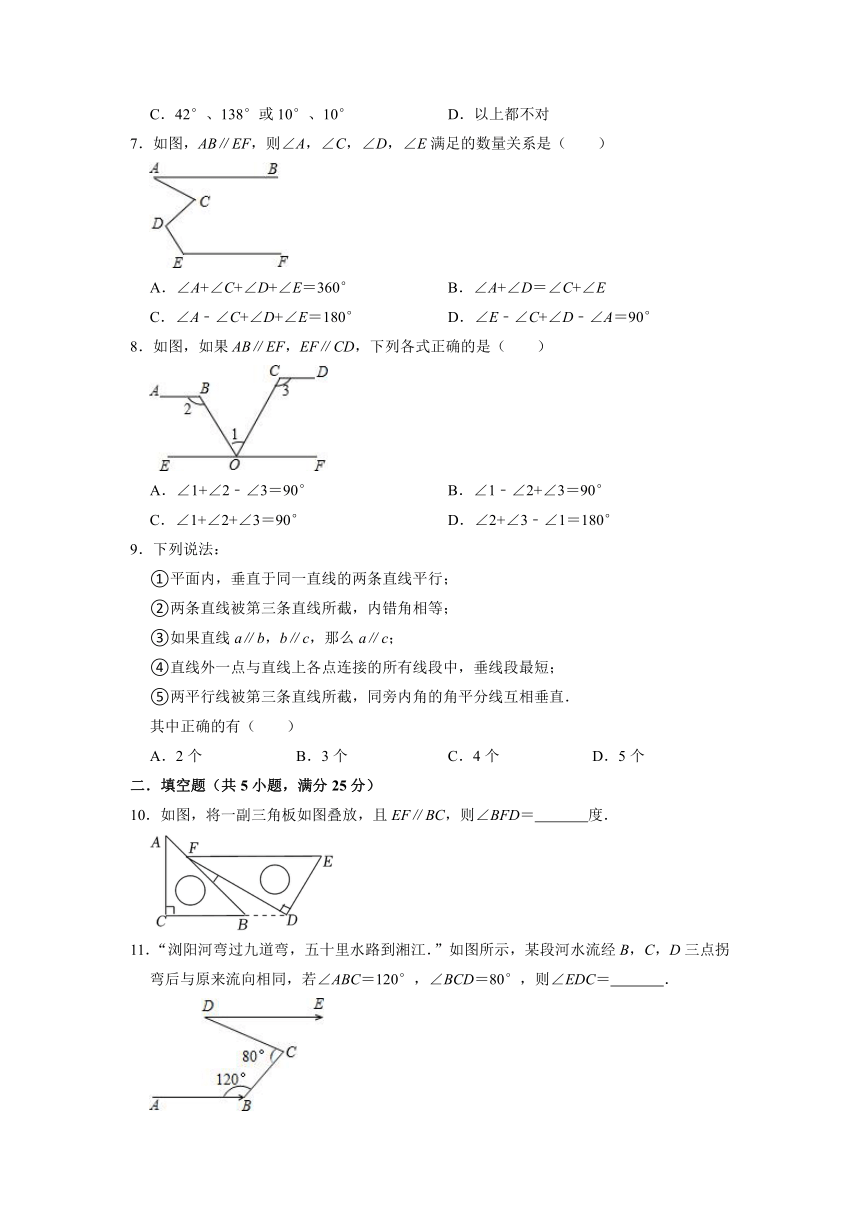
7.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
8.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2﹣∠3=90° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3﹣∠1=180°
9.下列说法:
①平面内,垂直于同一直线的两条直线平行;
②两条直线被第三条直线所截,内错角相等;
③如果直线a∥b,b∥c,那么a∥c;
④直线外一点与直线上各点连接的所有线段中,垂线段最短;
⑤两平行线被第三条直线所截,同旁内角的角平分线互相垂直.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共5小题,满分25分)
10.如图,将一副三角板如图叠放,且EF∥BC,则∠BFD= 度.
11.“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经B,C,D三点拐弯后与原来流向相同,若∠ABC=120°,∠BCD=80°,则∠EDC= .
12.把一张对边互相平行的纸条折成如图那样,EF是折痕,若∠EFB=32°,则∠D′FD的度数为 .
13.如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC= °.
14.如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
三.解答题(共6小题,满分50分)
15.如图,已知射线AM∥BN,连结AB,点C是射线BN上的一个动点(与点B不重合),AD,AE分别平分∠BAC和∠CAM,交射线BN于点D,E.
(1)试说明:∠ACB=2∠AEB;
(2)若∠ADB﹣∠BAD=45°,求∠AEB的度数.
16.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,那么EF平分∠DEB吗?
解:∵CD平分∠ACB(已知),
∴∠1=∠2( ),
∵AC∥DE(已知),
∴∠1=∠ ,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3( ),∠2=∠5( ),
∴∠4=∠5(等量代换).
∴EF平分∠DEB.
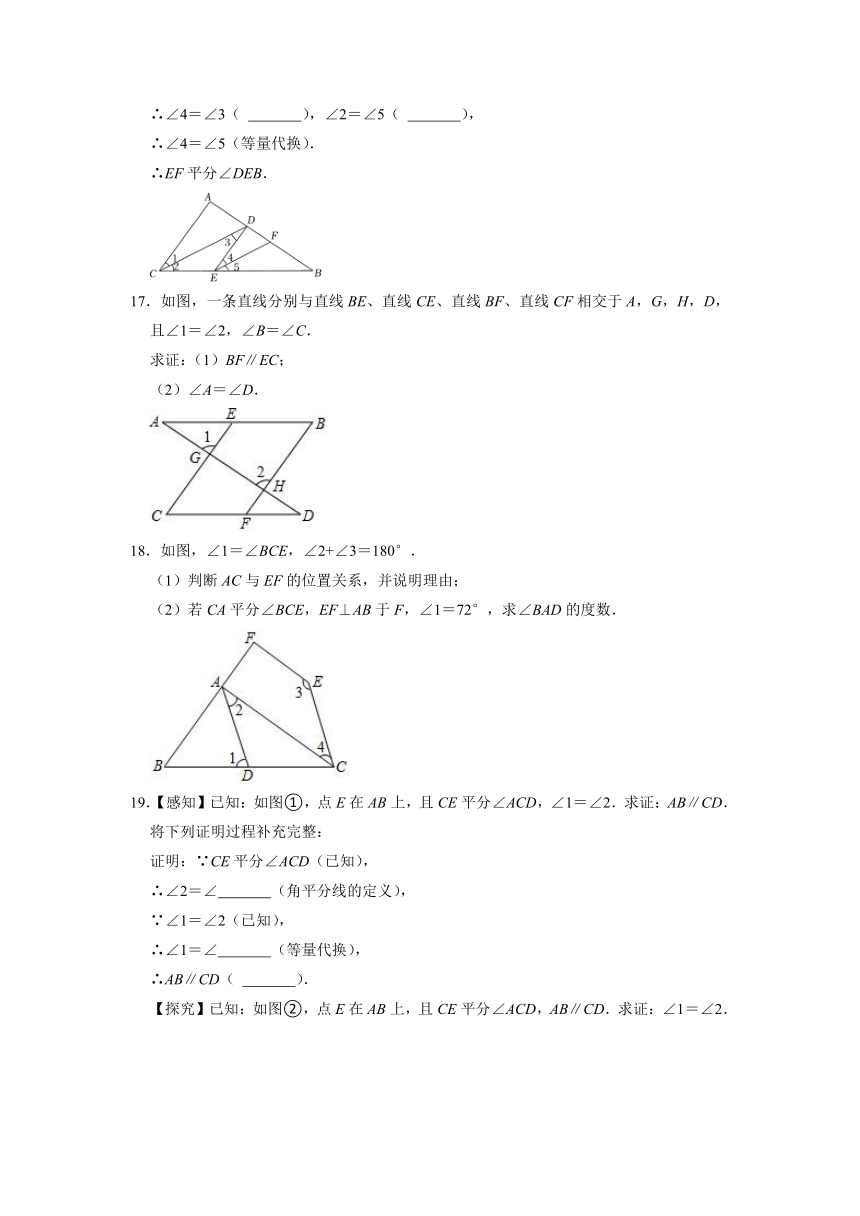
17.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A,G,H,D,且∠1=∠2,∠B=∠C.
求证:(1)BF∥EC;
(2)∠A=∠D.
18.如图,∠1=∠BCE,∠2+∠3=180°.
(1)判断AC与EF的位置关系,并说明理由;
(2)若CA平分∠BCE,EF⊥AB于F,∠1=72°,求∠BAD的度数.
19.【感知】已知:如图①,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
将下列证明过程补充完整:
证明:∵CE平分∠ACD(已知),
∴∠2=∠ (角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴AB∥CD( ).
【探究】已知:如图②,点E在AB上,且CE平分∠ACD,AB∥CD.求证:∠1=∠2.
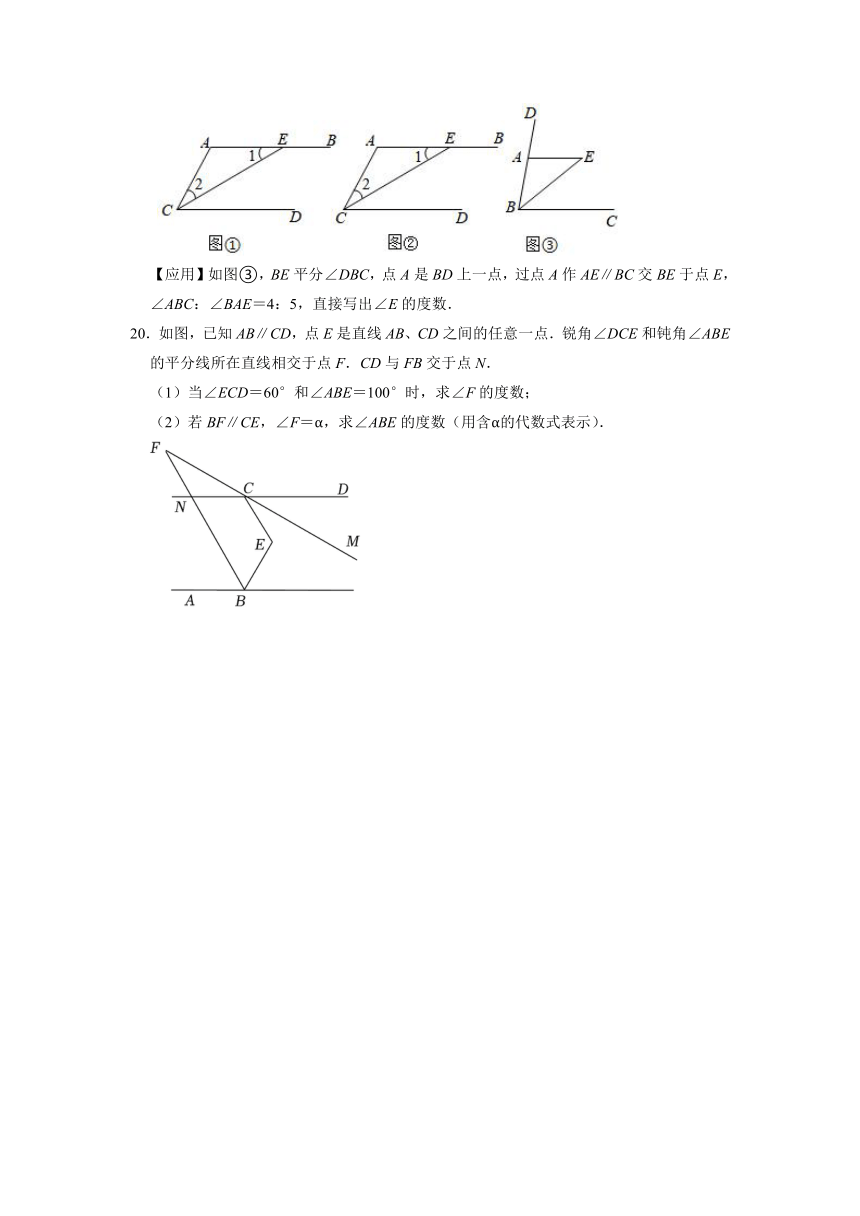
【应用】如图③,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC:∠BAE=4:5,直接写出∠E的度数.
20.如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.
(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;
(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).
参考答案
一.选择题(共9小题,满分45分)
1.解:∵AB∥CD,
∴∠1=∠3,
∵∠2+∠3=180°,
∴∠1+∠2=180°,
∵∠2=2∠1﹣6°,
∴∠1+2∠1﹣6=180°,
解得∠1=62°,
∴∠2=2×62﹣6=118°,
故选:B.
2.解:由题意得∠ADF=45°,
∵FD∥AB,∠B=30°,
∴∠B+∠BDF=180°,
∴∠BDF=180°﹣∠B=150°,
∴∠ADB=∠BDF﹣∠ADF=105°.
故选:B.
3.解:∵AD⊥CE于点A,
∴∠CAD=90°,
∵∠1=60°,
∴∠ACD=90°﹣∠1=30°,
∵AB∥CD,
∴∠2=∠ACD=30°.
故选:A.
4.解:∵AB∥CD,
∴∠BCD=∠1①.
∵CD∥EF,
∴∠DCE=180°﹣∠2②,
∴∠BCE=∠BCD+∠DCE=180°﹣∠2+∠1.
故选:D.
5.解:延长DC交AB与G,延长CD交EF于H.
在直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,即α+β﹣γ=90°.
故选:C.
6.解:如图1,∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2.
如图2,∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°
∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
设另一个角为x,则这一个角为4x﹣30°,
(1)两个角相等,则x=4x﹣30°,
解得x=10°,
4x﹣30°=4×10°﹣30°=10°;
(2)两个角互补,则x+(4x﹣30°)=180°,
解得x=42°,
4x﹣30°=4×42°﹣30°=138°.
所以这两个角是42°、138°或10°、10°.
故选:C.
7.解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠C=∠ACG+∠CDH=∠A+∠D﹣(180°﹣∠E),
∴∠A﹣∠C+∠D+∠E=180°.
故选:C.
8.解:
∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
即∠2+∠3﹣∠1=180°,
故选:D.
9.解:①平面内,垂直于同一直线的两条直线平行,原说法正确;
②两条平行线被第三条直线所截,内错角相等,原说法错误;
③如果直线a∥b,b∥c,那么a∥c,原说法正确;
④直线外一点与直线上各点连接的所有线段中,垂线段最短,原说法正确;
⑤两条平行线被第三条直线所截,同旁内角的角平分线互相垂直,原说法正确.
其中正确的是①③④⑤,共4个.
故选:C.
二.填空题(共5小题,满分25分)
10.解:由题意得,∠ABC=45°,∠DFE=30°,
∵EF∥BC,
∴∠BFE=∠ABC=45°,
∴∠BFD=45°﹣30°=15°.
故答案为:15.
11.解:由题意得,AB∥DE,
过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20°.
12.解:∵EF 是折痕,∠EFB=32°,AC′∥BD′,
∴∠C′EF=∠GEF=32°,
∴∠C′EG=64°,
∵CE∥FD,
∴∠D′FD=∠EGB=64°.
故答案为:64°.
13.解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°﹣∠ECD=180°﹣150°=30°,
∴∠BEC=∠BEF﹣∠CEF=40°;
故答案为:40.
14.解:如图所示,延长AP交直线b于C,
∵a∥b,
∴∠C=∠1=35°,
∵∠APB是△BCP的外角,PA⊥PB,
∴∠2=∠APB﹣∠C=90°﹣35°=55°,
故答案为:55°.
三.解答题(共6小题,满分50分)
15.解:(1)∵AE分别平分∠CAM,
∴∠CAM=2∠EAM.
∵AM∥BN,
∴∠CAM=∠ACB,∠EAM=∠AEB.
∴∠ACB=2∠AEB.
(2)∵AM∥BN,
∴∠CAM=∠ACB,∠ADB=∠DAM.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠ADB﹣∠BAD=45°,
∴∠DAM﹣∠CAD=45°.
∴∠CAM=∠ACB=45°.
由(1)知∠ACB=2∠AEB,
∴∠AEB=22.5°.
16.解:∵CD平分∠ACB(已知),
∴∠1=∠2(角平分线的定义),
∵AC∥DE(已知),
∴∠1=∠3,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3(两直线平行,内错角相等),∠2=∠5(两直线平行,同位角相等),
∴∠4=∠5(等量代换).
故答案为:角平分线的定义;3;两直线平行,内错角相等;两直线平行,同位角相等.
17.证明:(1)∵∠1=∠2(已知),
∴BF∥EC(同位角相等,两直线平行);
(2)∵BF∥EC(已证),
∴∠C=∠BFD(两直线平行,同位角相等),
∵∠B=∠C(已知),
∴∠B=∠BFD(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等).
18.解:(1)AC∥EF.理由:
∵∠1=∠BCE,
∴AD∥CE.
∴∠2=∠4.
∵∠2+∠3=180°,
∴∠4+∠3=180°.
∴EF∥AC.
(2)∵AD∥EC,CA平分∠BCE,
∴∠ACD=∠4=∠2.
∵∠1=72°,
∴∠2=36°.
∵EF∥AC,EF⊥AB于F,
∴∠BAC=∠F=90°.
∴∠BAD=∠BAC﹣∠2
=54°.
19.【感知】解:∵CE平分∠ACD(已知),
∴∠2=∠DCE(角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠DCE(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:DCE;DCE;内错角相等,两直线平行;
【探究】证明:∵CE平分∠ACD,
∴∠2=∠DCE,
∵AB∥CD,
∴∠1=∠DCE,
∴∠1=∠2;
【应用】∵BE平分∠DBC,
∴∠ABE=∠CBE,
∵AE∥BC,
∴∠ABC+∠BAE=180°,∠E=∠CBE,
∵∠ABC:∠BAE=4:5,
∴∠ABC=80°,
∴∠CBE=40°,
∴∠E=∠CBE=40°.
20.解:如图,过点F作FH//CD,
∵锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F,∠ECD=60°,∠ABE=100°,
∴∠DCM=∠ECM=30°,∠ABN=∠EBN=50°°,
∴∠NCF=30°,
∵AB∥CD,FH//CD,
∴FH∥AB,
∴∠HFB=∠ABN=50°,∠HFC=∠FCN=30°,
∴∠BFC=20°.
(2)如图,
∵BF∥CE,
∴∠ECM=∠BFM=α,
∴∠DCE=∠DNB=2α,
∵AB∥CD
∴∠ABN=∠BNC=2α,
∴∠ABE=4α.
一.选择题(共9小题,满分45分)
1.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于( )
A.116° B.118° C.120° D.124°
2.一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FD∥AB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
3.如图,AB∥CD,AD⊥CE于点A,∠1=60°,则∠2的度数是( )
A.30° B.40° C.45° D.60°
4.如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2 B.∠2=2∠1 C.180°﹣∠1﹣∠2 D.180°﹣∠2+∠1
5.如图,AB∥EF,∠C=90°,则α、β和γ的关系是( )
A.β=α+γ B.α+β+γ=180° C.α+β﹣γ=90° D.β+γ﹣α=180°
6.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.42°、138° B.都是10°
C.42°、138°或10°、10° D.以上都不对
7.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
8.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2﹣∠3=90° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3﹣∠1=180°
9.下列说法:
①平面内,垂直于同一直线的两条直线平行;
②两条直线被第三条直线所截,内错角相等;
③如果直线a∥b,b∥c,那么a∥c;
④直线外一点与直线上各点连接的所有线段中,垂线段最短;
⑤两平行线被第三条直线所截,同旁内角的角平分线互相垂直.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共5小题,满分25分)
10.如图,将一副三角板如图叠放,且EF∥BC,则∠BFD= 度.
11.“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经B,C,D三点拐弯后与原来流向相同,若∠ABC=120°,∠BCD=80°,则∠EDC= .
12.把一张对边互相平行的纸条折成如图那样,EF是折痕,若∠EFB=32°,则∠D′FD的度数为 .
13.如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC= °.
14.如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
三.解答题(共6小题,满分50分)
15.如图,已知射线AM∥BN,连结AB,点C是射线BN上的一个动点(与点B不重合),AD,AE分别平分∠BAC和∠CAM,交射线BN于点D,E.
(1)试说明:∠ACB=2∠AEB;
(2)若∠ADB﹣∠BAD=45°,求∠AEB的度数.
16.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,那么EF平分∠DEB吗?
解:∵CD平分∠ACB(已知),
∴∠1=∠2( ),
∵AC∥DE(已知),
∴∠1=∠ ,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3( ),∠2=∠5( ),
∴∠4=∠5(等量代换).
∴EF平分∠DEB.
17.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A,G,H,D,且∠1=∠2,∠B=∠C.
求证:(1)BF∥EC;
(2)∠A=∠D.
18.如图,∠1=∠BCE,∠2+∠3=180°.
(1)判断AC与EF的位置关系,并说明理由;
(2)若CA平分∠BCE,EF⊥AB于F,∠1=72°,求∠BAD的度数.
19.【感知】已知:如图①,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
将下列证明过程补充完整:
证明:∵CE平分∠ACD(已知),
∴∠2=∠ (角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴AB∥CD( ).
【探究】已知:如图②,点E在AB上,且CE平分∠ACD,AB∥CD.求证:∠1=∠2.
【应用】如图③,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC:∠BAE=4:5,直接写出∠E的度数.
20.如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.
(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;
(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).
参考答案
一.选择题(共9小题,满分45分)
1.解:∵AB∥CD,
∴∠1=∠3,
∵∠2+∠3=180°,
∴∠1+∠2=180°,
∵∠2=2∠1﹣6°,
∴∠1+2∠1﹣6=180°,
解得∠1=62°,
∴∠2=2×62﹣6=118°,
故选:B.
2.解:由题意得∠ADF=45°,
∵FD∥AB,∠B=30°,
∴∠B+∠BDF=180°,
∴∠BDF=180°﹣∠B=150°,
∴∠ADB=∠BDF﹣∠ADF=105°.
故选:B.
3.解:∵AD⊥CE于点A,
∴∠CAD=90°,
∵∠1=60°,
∴∠ACD=90°﹣∠1=30°,
∵AB∥CD,
∴∠2=∠ACD=30°.
故选:A.
4.解:∵AB∥CD,
∴∠BCD=∠1①.
∵CD∥EF,
∴∠DCE=180°﹣∠2②,
∴∠BCE=∠BCD+∠DCE=180°﹣∠2+∠1.
故选:D.
5.解:延长DC交AB与G,延长CD交EF于H.
在直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,即α+β﹣γ=90°.
故选:C.
6.解:如图1,∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2.
如图2,∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°
∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
设另一个角为x,则这一个角为4x﹣30°,
(1)两个角相等,则x=4x﹣30°,
解得x=10°,
4x﹣30°=4×10°﹣30°=10°;
(2)两个角互补,则x+(4x﹣30°)=180°,
解得x=42°,
4x﹣30°=4×42°﹣30°=138°.
所以这两个角是42°、138°或10°、10°.
故选:C.
7.解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠C=∠ACG+∠CDH=∠A+∠D﹣(180°﹣∠E),
∴∠A﹣∠C+∠D+∠E=180°.
故选:C.
8.解:
∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
即∠2+∠3﹣∠1=180°,
故选:D.
9.解:①平面内,垂直于同一直线的两条直线平行,原说法正确;
②两条平行线被第三条直线所截,内错角相等,原说法错误;
③如果直线a∥b,b∥c,那么a∥c,原说法正确;
④直线外一点与直线上各点连接的所有线段中,垂线段最短,原说法正确;
⑤两条平行线被第三条直线所截,同旁内角的角平分线互相垂直,原说法正确.
其中正确的是①③④⑤,共4个.
故选:C.
二.填空题(共5小题,满分25分)
10.解:由题意得,∠ABC=45°,∠DFE=30°,
∵EF∥BC,
∴∠BFE=∠ABC=45°,
∴∠BFD=45°﹣30°=15°.
故答案为:15.
11.解:由题意得,AB∥DE,
过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20°.
12.解:∵EF 是折痕,∠EFB=32°,AC′∥BD′,
∴∠C′EF=∠GEF=32°,
∴∠C′EG=64°,
∵CE∥FD,
∴∠D′FD=∠EGB=64°.
故答案为:64°.
13.解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°﹣∠ECD=180°﹣150°=30°,
∴∠BEC=∠BEF﹣∠CEF=40°;
故答案为:40.
14.解:如图所示,延长AP交直线b于C,
∵a∥b,
∴∠C=∠1=35°,
∵∠APB是△BCP的外角,PA⊥PB,
∴∠2=∠APB﹣∠C=90°﹣35°=55°,
故答案为:55°.
三.解答题(共6小题,满分50分)
15.解:(1)∵AE分别平分∠CAM,
∴∠CAM=2∠EAM.
∵AM∥BN,
∴∠CAM=∠ACB,∠EAM=∠AEB.
∴∠ACB=2∠AEB.
(2)∵AM∥BN,
∴∠CAM=∠ACB,∠ADB=∠DAM.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠ADB﹣∠BAD=45°,
∴∠DAM﹣∠CAD=45°.
∴∠CAM=∠ACB=45°.
由(1)知∠ACB=2∠AEB,
∴∠AEB=22.5°.
16.解:∵CD平分∠ACB(已知),
∴∠1=∠2(角平分线的定义),
∵AC∥DE(已知),
∴∠1=∠3,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3(两直线平行,内错角相等),∠2=∠5(两直线平行,同位角相等),
∴∠4=∠5(等量代换).
故答案为:角平分线的定义;3;两直线平行,内错角相等;两直线平行,同位角相等.
17.证明:(1)∵∠1=∠2(已知),
∴BF∥EC(同位角相等,两直线平行);
(2)∵BF∥EC(已证),
∴∠C=∠BFD(两直线平行,同位角相等),
∵∠B=∠C(已知),
∴∠B=∠BFD(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等).
18.解:(1)AC∥EF.理由:
∵∠1=∠BCE,
∴AD∥CE.
∴∠2=∠4.
∵∠2+∠3=180°,
∴∠4+∠3=180°.
∴EF∥AC.
(2)∵AD∥EC,CA平分∠BCE,
∴∠ACD=∠4=∠2.
∵∠1=72°,
∴∠2=36°.
∵EF∥AC,EF⊥AB于F,
∴∠BAC=∠F=90°.
∴∠BAD=∠BAC﹣∠2
=54°.
19.【感知】解:∵CE平分∠ACD(已知),
∴∠2=∠DCE(角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠DCE(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:DCE;DCE;内错角相等,两直线平行;
【探究】证明:∵CE平分∠ACD,
∴∠2=∠DCE,
∵AB∥CD,
∴∠1=∠DCE,
∴∠1=∠2;
【应用】∵BE平分∠DBC,
∴∠ABE=∠CBE,
∵AE∥BC,
∴∠ABC+∠BAE=180°,∠E=∠CBE,
∵∠ABC:∠BAE=4:5,
∴∠ABC=80°,
∴∠CBE=40°,
∴∠E=∠CBE=40°.
20.解:如图,过点F作FH//CD,
∵锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F,∠ECD=60°,∠ABE=100°,
∴∠DCM=∠ECM=30°,∠ABN=∠EBN=50°°,
∴∠NCF=30°,
∵AB∥CD,FH//CD,
∴FH∥AB,
∴∠HFB=∠ABN=50°,∠HFC=∠FCN=30°,
∴∠BFC=20°.
(2)如图,
∵BF∥CE,
∴∠ECM=∠BFM=α,
∴∠DCE=∠DNB=2α,
∵AB∥CD
∴∠ABN=∠BNC=2α,
∴∠ABE=4α.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
