2021-2022学年湘教版七年级数学下册2.2.1平方差公式同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版七年级数学下册2.2.1平方差公式同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:21:15 | ||
图片预览


文档简介
2021-2022学年湘教版七年级数学下册《2-2-1平方差公式》同步练习题(附答案)
1.下列运算正确的是( )
A.(5﹣m)(5+m)=m2﹣25 B.(1﹣3m)(1+3m)=1﹣3m2
C.(﹣4﹣3n)(﹣4+3n)=﹣9n2+16 D.(2ab﹣n)(2ab+n)=4ab2﹣n2
2.计算(x+1)(x﹣1)(x2+1)的结果是( )
A.x2﹣1 B.x3﹣1 C.x4+1 D.x4﹣1
3.计算(2m﹣3n)(﹣2m﹣3n)的结果是( )
A.﹣4m2+9n2 B.﹣4m2﹣9n2 C.4m2﹣9n2 D.4m2+9n2
4.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户王老汉,第二年,他对王老汉说:“我把这块地的一边增加6米,相邻的另边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得王老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
5.下列算式中不能利用平方差公式计算的是( )
A.(x+y)(x﹣y) B.(x﹣y)(﹣x﹣y)
C.(x﹣y)(﹣x+y) D.(x+y)(y﹣x)
6.(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232﹣1 B.232+1 C.232 D.216
7.已知a+b=3,a﹣b=1,则a2﹣b2= .
8.若(2m+5)(2m﹣5)=15,则m2= .
9.(2x﹣3y﹣1)(2x+3y+1)=[2x﹣( )][2x+( )].
10.计算(﹣s+t)(﹣s﹣t)= .
11.若x2﹣y2=16,x+y=8,则x﹣y= .
12.已知a2+a﹣1=0,则代数式(a+2)(a﹣2)+a(a+2)值为 .
13.若(x2+y2+1)(x2+y2﹣1)=48,则x2+y2=
14.街心花园有一块边长为a米的正方形草坪,经统一规划后,南北向要加长3米,而东西向要缩短3米,问改造后的长方形草坪的面积是 平方米.
15.计算:2022×2020﹣20212的结果为 .
16.已知m﹣n=3,则m2﹣n2﹣6n的值 .
17.计算:3(2x﹣1)﹣(﹣3x﹣4)(3x﹣4)
18.用平方差公式计算:
(1)30.8×29.2; (2)20192﹣2018×2020.
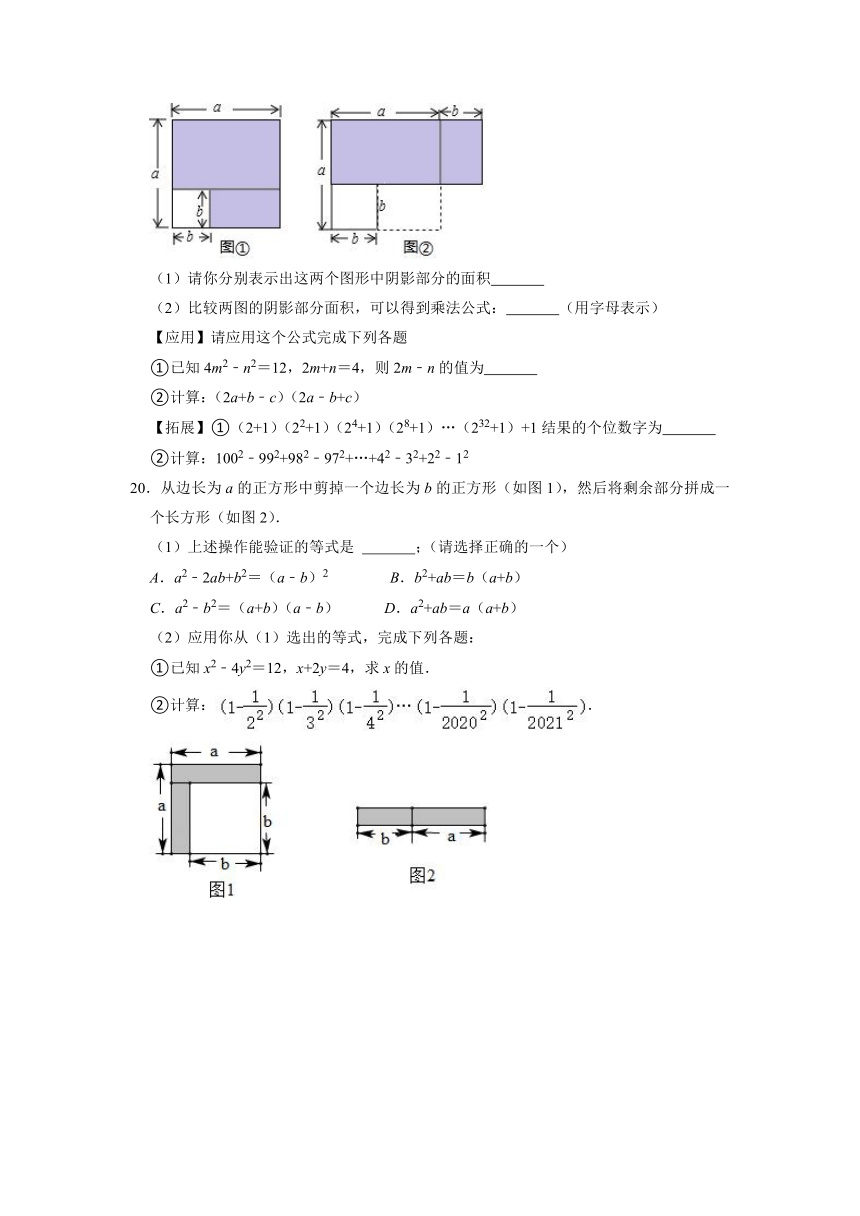
19.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
20.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2 B.b2+ab=b(a+b)
C.a2﹣b2=(a+b)(a﹣b) D.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x的值.
②计算:.
参考答案
1.解:A、(5﹣m)(5+m)=25﹣m2,错误;
B、(1﹣3m)(1+3m)=1﹣9m2,错误;
C、(﹣4﹣3n)(﹣4+3n)=﹣9n2+16,正确;
D、(2ab﹣n)(2ab+n)=4a2b2﹣n2,错误;
故选:C.
2.解:原式=(x2﹣1)(x2+1)
=x4﹣1.
故选:D.
3.解:(2m﹣3n)(﹣2m﹣3n)=(﹣3n)2﹣(2m)2=﹣4m2+9n2,
故选:A.
4.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
5.解:A、原式=x2﹣y2,不符合题意;
B、原式=y2﹣x2,不符合题意;
C、原式=﹣(x﹣y)2=﹣x2+2xy﹣y2,符合题意;
D、原式=y2﹣x2,不符合题意.
故选:C.
6.解:原式=(2﹣1)(2+1)(22+1)(24+1)…(216+1)
=(22﹣1)(22+1)(24+1)…(216+1)
=(24﹣1)(24+1)…(216+1)
=(28﹣1)…(216+1)
=232﹣1,
故选:A.
7.解:∵a+b=3,a﹣b=1,
∴a2﹣b2=(a+b)(a﹣b)=3×1=3.
故答案为:3.
8.解:由(2m+5)(2m﹣5)=15,得4m2﹣25=15.
解得m2=10.
故答案是:10.
9.解:原式=[2x﹣( 3y+1)][2x+( 3y+1)].
故答案是:3y+1.
10.解:(﹣s+t)(﹣s﹣t)
=(﹣s)2﹣t2
=s2﹣t2.
故答案为:s2﹣t2.
11.解:∵x2﹣y2=(x+y)(x﹣y)=16,x+y=8,
∴x﹣y=16÷8=2.
故答案为:2.
12.解:(a+2)(a﹣2)+a(a+2)
=a2﹣4+a2+2a
=2a2+2a﹣4
=2(a2+a)﹣4.
∵a2+a﹣1=0,
∴a2+a=1.
∴原式=2×1﹣4=﹣2.
故答案为:﹣2.
13.解:因为(x2+y2+1)(x2+y2﹣1)=48,
所以(x2+y2)2﹣12=48,
所以(x2+y2)2=49,
x2+y2=±7(负值舍去).
故答案为:7.
14.解:改造后长方形草坪的面积是:
(a+3)(a﹣3)=a2﹣9(平方米).
故改造后的长方形草坪的面积是a2﹣9平方米.
故答案为:a2﹣9.
15.解:原式=(2021+1)(2021﹣1)﹣20212=20212﹣1﹣20212=﹣1.
故答案为:﹣1.
16.解:∵m﹣n=3,
∴原式=(m﹣n)(m+n)﹣6n=3(m+n)﹣6n=3m﹣3n=3(m﹣n)=9..
故答案为:9.
17.解:原式=6x﹣3﹣(16﹣9x2)
=6x﹣3﹣16+9x2
=9x2+6x﹣19.
18.解:(1)30.8×29.2
=(30+0.8)×(30﹣0.8)
=302﹣0.82
=900﹣0.64
=899.36;
(2)20192﹣2018×2020
=20192﹣(2019﹣1)×(2019+1)
=20192﹣20192+1
=1.
19.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)
=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2
=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1
=(216﹣1)…(232+1)+1
=264﹣1+1
=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
20.解:(1)第一个图形中阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故选:C;
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),
∴12=4(x﹣2y),
得:x﹣2y=3,
联立,
①+②,得2x=7,
解得:x=;
②
=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)
=
=×
=.
1.下列运算正确的是( )
A.(5﹣m)(5+m)=m2﹣25 B.(1﹣3m)(1+3m)=1﹣3m2
C.(﹣4﹣3n)(﹣4+3n)=﹣9n2+16 D.(2ab﹣n)(2ab+n)=4ab2﹣n2
2.计算(x+1)(x﹣1)(x2+1)的结果是( )
A.x2﹣1 B.x3﹣1 C.x4+1 D.x4﹣1
3.计算(2m﹣3n)(﹣2m﹣3n)的结果是( )
A.﹣4m2+9n2 B.﹣4m2﹣9n2 C.4m2﹣9n2 D.4m2+9n2
4.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户王老汉,第二年,他对王老汉说:“我把这块地的一边增加6米,相邻的另边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得王老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
5.下列算式中不能利用平方差公式计算的是( )
A.(x+y)(x﹣y) B.(x﹣y)(﹣x﹣y)
C.(x﹣y)(﹣x+y) D.(x+y)(y﹣x)
6.(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232﹣1 B.232+1 C.232 D.216
7.已知a+b=3,a﹣b=1,则a2﹣b2= .
8.若(2m+5)(2m﹣5)=15,则m2= .
9.(2x﹣3y﹣1)(2x+3y+1)=[2x﹣( )][2x+( )].
10.计算(﹣s+t)(﹣s﹣t)= .
11.若x2﹣y2=16,x+y=8,则x﹣y= .
12.已知a2+a﹣1=0,则代数式(a+2)(a﹣2)+a(a+2)值为 .
13.若(x2+y2+1)(x2+y2﹣1)=48,则x2+y2=
14.街心花园有一块边长为a米的正方形草坪,经统一规划后,南北向要加长3米,而东西向要缩短3米,问改造后的长方形草坪的面积是 平方米.
15.计算:2022×2020﹣20212的结果为 .
16.已知m﹣n=3,则m2﹣n2﹣6n的值 .
17.计算:3(2x﹣1)﹣(﹣3x﹣4)(3x﹣4)
18.用平方差公式计算:
(1)30.8×29.2; (2)20192﹣2018×2020.
19.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
20.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2 B.b2+ab=b(a+b)
C.a2﹣b2=(a+b)(a﹣b) D.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x的值.
②计算:.
参考答案
1.解:A、(5﹣m)(5+m)=25﹣m2,错误;
B、(1﹣3m)(1+3m)=1﹣9m2,错误;
C、(﹣4﹣3n)(﹣4+3n)=﹣9n2+16,正确;
D、(2ab﹣n)(2ab+n)=4a2b2﹣n2,错误;
故选:C.
2.解:原式=(x2﹣1)(x2+1)
=x4﹣1.
故选:D.
3.解:(2m﹣3n)(﹣2m﹣3n)=(﹣3n)2﹣(2m)2=﹣4m2+9n2,
故选:A.
4.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
5.解:A、原式=x2﹣y2,不符合题意;
B、原式=y2﹣x2,不符合题意;
C、原式=﹣(x﹣y)2=﹣x2+2xy﹣y2,符合题意;
D、原式=y2﹣x2,不符合题意.
故选:C.
6.解:原式=(2﹣1)(2+1)(22+1)(24+1)…(216+1)
=(22﹣1)(22+1)(24+1)…(216+1)
=(24﹣1)(24+1)…(216+1)
=(28﹣1)…(216+1)
=232﹣1,
故选:A.
7.解:∵a+b=3,a﹣b=1,
∴a2﹣b2=(a+b)(a﹣b)=3×1=3.
故答案为:3.
8.解:由(2m+5)(2m﹣5)=15,得4m2﹣25=15.
解得m2=10.
故答案是:10.
9.解:原式=[2x﹣( 3y+1)][2x+( 3y+1)].
故答案是:3y+1.
10.解:(﹣s+t)(﹣s﹣t)
=(﹣s)2﹣t2
=s2﹣t2.
故答案为:s2﹣t2.
11.解:∵x2﹣y2=(x+y)(x﹣y)=16,x+y=8,
∴x﹣y=16÷8=2.
故答案为:2.
12.解:(a+2)(a﹣2)+a(a+2)
=a2﹣4+a2+2a
=2a2+2a﹣4
=2(a2+a)﹣4.
∵a2+a﹣1=0,
∴a2+a=1.
∴原式=2×1﹣4=﹣2.
故答案为:﹣2.
13.解:因为(x2+y2+1)(x2+y2﹣1)=48,
所以(x2+y2)2﹣12=48,
所以(x2+y2)2=49,
x2+y2=±7(负值舍去).
故答案为:7.
14.解:改造后长方形草坪的面积是:
(a+3)(a﹣3)=a2﹣9(平方米).
故改造后的长方形草坪的面积是a2﹣9平方米.
故答案为:a2﹣9.
15.解:原式=(2021+1)(2021﹣1)﹣20212=20212﹣1﹣20212=﹣1.
故答案为:﹣1.
16.解:∵m﹣n=3,
∴原式=(m﹣n)(m+n)﹣6n=3(m+n)﹣6n=3m﹣3n=3(m﹣n)=9..
故答案为:9.
17.解:原式=6x﹣3﹣(16﹣9x2)
=6x﹣3﹣16+9x2
=9x2+6x﹣19.
18.解:(1)30.8×29.2
=(30+0.8)×(30﹣0.8)
=302﹣0.82
=900﹣0.64
=899.36;
(2)20192﹣2018×2020
=20192﹣(2019﹣1)×(2019+1)
=20192﹣20192+1
=1.
19.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)
=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2
=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1
=(216﹣1)…(232+1)+1
=264﹣1+1
=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
20.解:(1)第一个图形中阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故选:C;
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),
∴12=4(x﹣2y),
得:x﹣2y=3,
联立,
①+②,得2x=7,
解得:x=;
②
=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)
=
=×
=.
