九年级数学湘教版上册3.4 相似三角形的判定与性质(一) 导学案(无答案)
文档属性
| 名称 | 九年级数学湘教版上册3.4 相似三角形的判定与性质(一) 导学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 11:14:25 | ||
图片预览

文档简介
相似三角形的判定与性质(一)
一、教学目标:
1、熟练地掌握“两角分别相等的两个三角形相似”的判定方法和相似三角形的有关性质;
2、以问题为载体,发展学生有条理地分析问题的能力,体会数学知识间的内在联系;
3、通过对图形的变化,能将复杂问题抽象并转化成常见的几何图形,运用“从特殊到一般,再从一般到特殊”的方法研究数学问题。
二、复习重、难点:
1、重点:熟练掌握“两角分别相等的两个三角形相似”的判定方法和相似三角形的有关性质;
2、难点:有条理地分析问题,将复杂问题抽象并转化成常见的几何图形,灵活运用所学知识解决数学综合性问题。
三、教学过程:
(一)问题设置 知识梳理
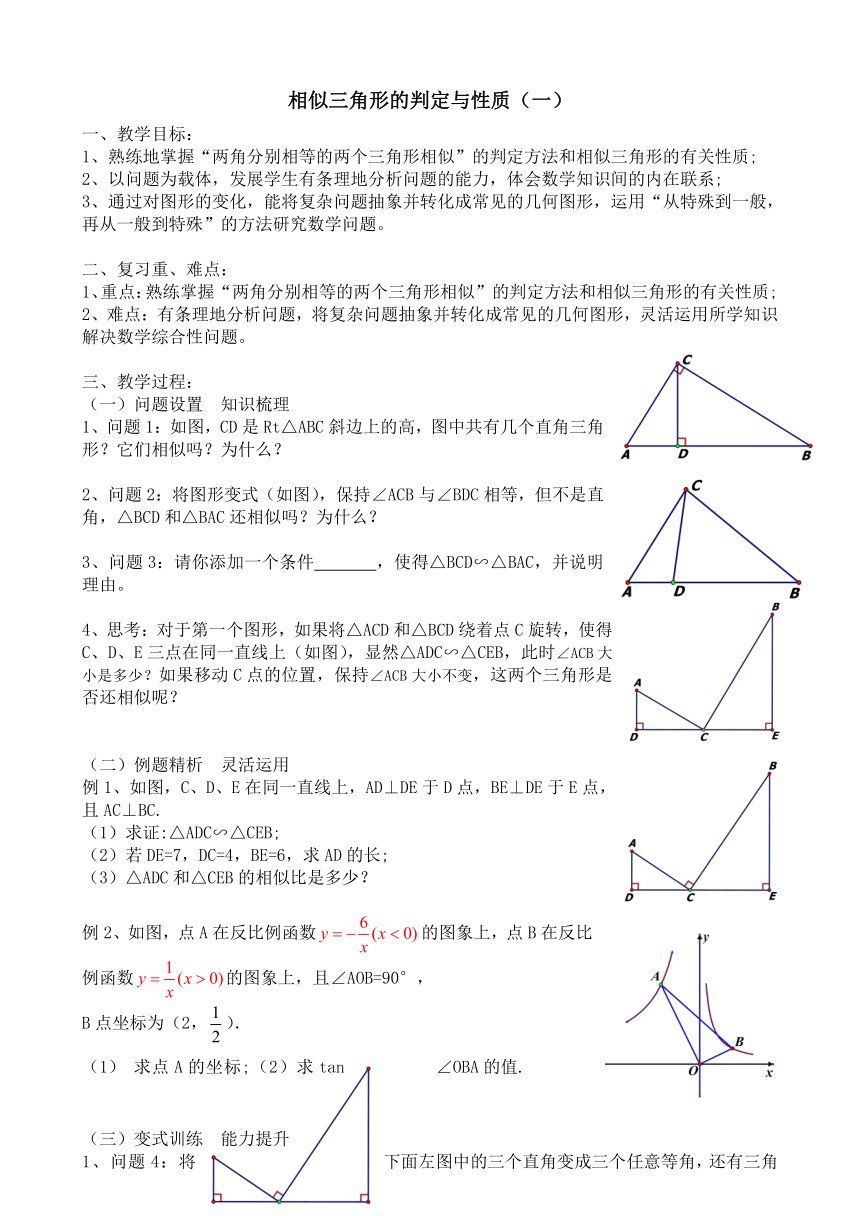
1、问题1:如图,CD是Rt△ABC斜边上的高,图中共有几个直角三角形?它们相似吗?为什么?
2、问题2:将图形变式(如图),保持∠ACB与∠BDC相等,但不是直角,△BCD和△BAC还相似吗?为什么?
3、问题3:请你添加一个条件 ,使得△BCD∽△BAC,并说明理由。
4、思考:对于第一个图形,如果将△ACD和△BCD绕着点C旋转,使得C、D、E三点在同一直线上(如图),显然△ADC∽△CEB,此时∠ACB大小是多少?如果移动C点的位置,保持∠ACB大小不变,这两个三角形是否还相似呢?
(二)例题精析 灵活运用
例1、如图,C、D、E在同一直线上,AD⊥DE于D点,BE⊥DE于E点,且AC⊥BC.
(1)求证:△ADC∽△CEB;
(2)若DE=7,DC=4,BE=6,求AD的长;
(3)△ADC和△CEB的相似比是多少?
例2、如图,点A在反比例函数的图象上,点B在反比例函数的图象上,且∠AOB=90°,
B点坐标为(2,).
求点A的坐标;(2)求tan∠OBA的值.
(三)变式训练 能力提升
1、问题4:将下面左图中的三个直角变成三个任意等角,还有三角形相似吗? 为什么?
2、变式练习:如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于F,ME交BC于G.连接FG,如果AB=,AF=3,求FG的长.
(四)总结反思 提炼升华
通过本节课的复习,谈谈你的收获,还有哪些疑惑?
(五)分层作业 共同进步
1、必做题:复习练习册第46页第1题至第6题;
2、选做题:如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF.连接AF,求AF长度的最小值.
一、教学目标:
1、熟练地掌握“两角分别相等的两个三角形相似”的判定方法和相似三角形的有关性质;
2、以问题为载体,发展学生有条理地分析问题的能力,体会数学知识间的内在联系;
3、通过对图形的变化,能将复杂问题抽象并转化成常见的几何图形,运用“从特殊到一般,再从一般到特殊”的方法研究数学问题。
二、复习重、难点:
1、重点:熟练掌握“两角分别相等的两个三角形相似”的判定方法和相似三角形的有关性质;
2、难点:有条理地分析问题,将复杂问题抽象并转化成常见的几何图形,灵活运用所学知识解决数学综合性问题。
三、教学过程:
(一)问题设置 知识梳理
1、问题1:如图,CD是Rt△ABC斜边上的高,图中共有几个直角三角形?它们相似吗?为什么?
2、问题2:将图形变式(如图),保持∠ACB与∠BDC相等,但不是直角,△BCD和△BAC还相似吗?为什么?
3、问题3:请你添加一个条件 ,使得△BCD∽△BAC,并说明理由。
4、思考:对于第一个图形,如果将△ACD和△BCD绕着点C旋转,使得C、D、E三点在同一直线上(如图),显然△ADC∽△CEB,此时∠ACB大小是多少?如果移动C点的位置,保持∠ACB大小不变,这两个三角形是否还相似呢?
(二)例题精析 灵活运用
例1、如图,C、D、E在同一直线上,AD⊥DE于D点,BE⊥DE于E点,且AC⊥BC.
(1)求证:△ADC∽△CEB;
(2)若DE=7,DC=4,BE=6,求AD的长;
(3)△ADC和△CEB的相似比是多少?
例2、如图,点A在反比例函数的图象上,点B在反比例函数的图象上,且∠AOB=90°,
B点坐标为(2,).
求点A的坐标;(2)求tan∠OBA的值.
(三)变式训练 能力提升
1、问题4:将下面左图中的三个直角变成三个任意等角,还有三角形相似吗? 为什么?
2、变式练习:如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于F,ME交BC于G.连接FG,如果AB=,AF=3,求FG的长.
(四)总结反思 提炼升华
通过本节课的复习,谈谈你的收获,还有哪些疑惑?
(五)分层作业 共同进步
1、必做题:复习练习册第46页第1题至第6题;
2、选做题:如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF.连接AF,求AF长度的最小值.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
