沪科版数学八年级下册17.5 一元二次方程的应用 教案(表格式)
文档属性
| 名称 | 沪科版数学八年级下册17.5 一元二次方程的应用 教案(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 11:21:53 | ||
图片预览

文档简介
课 题 17.5 一元二次方程的应用
教 学目 标 知识与能力:会选用合理的方法解决一元二次方程的面积问题。 2、会根据实际面积问题中的数量关系列一元二次方程解应用题。 3、能根据具体问题的实际意义,检验结果是否合理。 过程与方法: 1、体验通过移动变化分析面积问题的方法。 发展学生应用数学的意思。 情感态度与价值观: 让学生体会一元二次方程是刻画现实世界一个有效的数学模型,感悟数学来源于生活,服务于生活;同时培养学生自我探索的兴趣和能力。 教学重点:运用一元二次方程探索和解决面积问题。 教学难点:面积问题中的等量分析
教 学 程 序 与 策 略
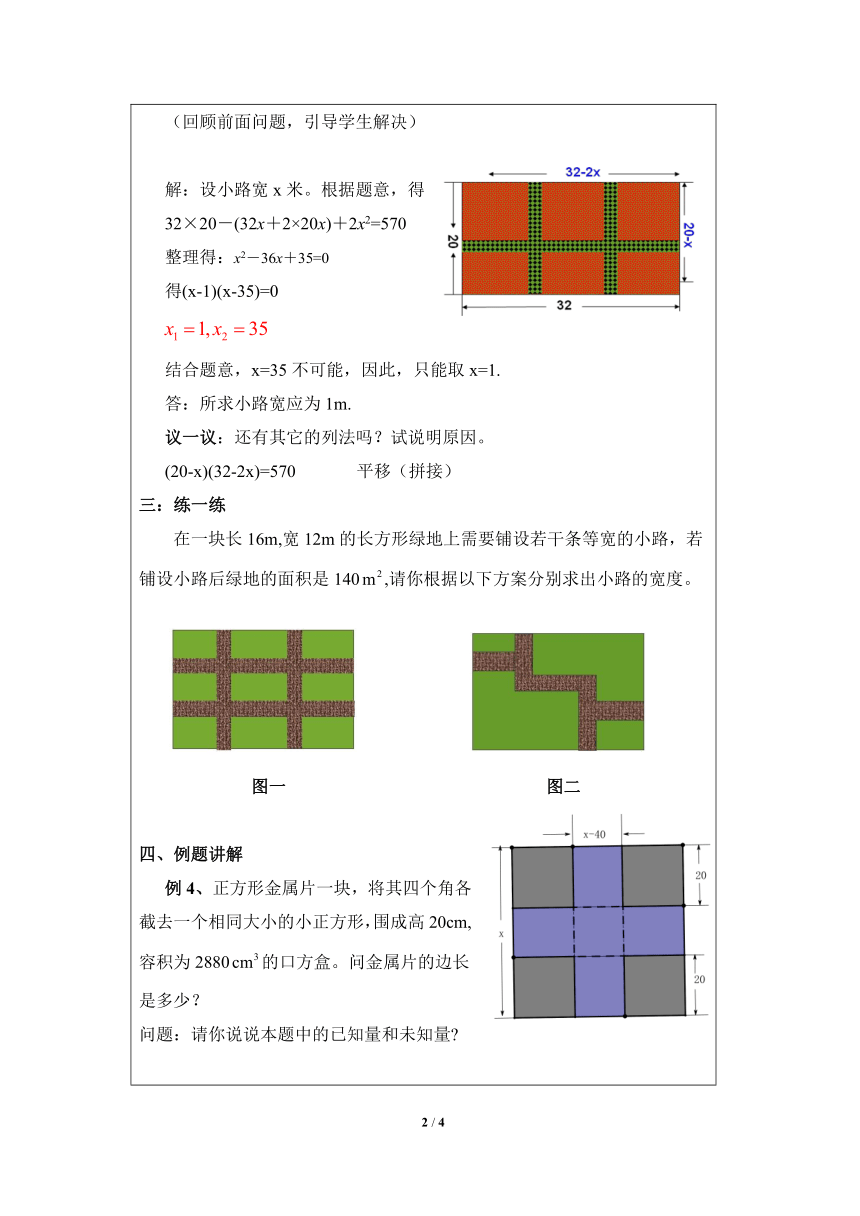
一:创设情境,引入新课提出问题:列方程解应用题的基本步骤有哪些?①审:审清题意:已知什么,求什么 已、未知之间有什么关系 ②设:设未知数,语句要完整,有单位(统一)的要注明单位;③列:列代数式,列方程;④解:解所列的方程;⑤验:是否是所列方程的根;是否符合题意;⑥答:答案也必需是完整的语句,注明单位.二:回顾问题1例1、在一块宽20m、长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把长方形空地分成大小一样的六块,建成小花坛。如图要使花坛的总面积为570 m2 ,问小路的宽应为多少?(回顾前面问题,引导学生解决)解:设小路宽x米。根据题意,得32×20-(32x+2×20x)+2x2=570整理得:x2-36x+35=0 得(x-1)(x-35)=0结合题意,x=35不可能,因此,只能取x=1.答:所求小路宽应为1m.议一议:还有其它的列法吗?试说明原因。(20-x)(32-2x)=570 平移(拼接)三:练一练在一块长16m,宽12m的长方形绿地上需要铺设若干条等宽的小路,若铺设小路后绿地的面积是140,请你根据以下方案分别求出小路的宽度。图一 图二四、例题讲解例4、正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20cm,容积为2880的口方盒。问金属片的边长是多少?问题:请你说说本题中的已知量和未知量 折叠前折叠后裁去小正方形边长20方盒的高20方盒的底面边长x-40正方形金属片的边长x方盒的底面积(x-40)2方盒的容积20(x-40)2解:设原金属片的边长为x cm。根据题意,得 20(x-40) = 2880解这个方程,得x=28不合题意,所以x=52答:原金属片的边长是52cm。五、练一练正方形金属片一块,将其四个角各截去一个边长为2cm的小正方形,围成容积为50cm3的开口方盒。问金属片的边长是多少?六、达标检测1、如图一,某小区一块长18m,宽6m的长方形空地,计划在其中修建两块相同的长方形绿地,它们的面积之和为60cm2,两块绿地之间及周边留有宽度相等的人行通道,若设人行道的宽度为x,则可以列出关于x的方程为 (不必化简)2、有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形
七、课堂小结: 提问:通过本堂课的学习,你学会了什么?列一元二次方程解应用题的一般步骤是:①审:审清题意:已知什么,求什么 已、未知之间有什么关系 ②设:设未知数,语句要完整,有单位(统一)的要注明单位;③列:列代数式,列方程;④解:解所列的方程;⑤验:是否是所列方程的根;是否符合题意;⑥答:答案也必需是完整的语句,注明单位且要贴近生活.
八、布置作业: 习题17.5第7题
九、教后反思
18m
6m
2 / 4
教 学目 标 知识与能力:会选用合理的方法解决一元二次方程的面积问题。 2、会根据实际面积问题中的数量关系列一元二次方程解应用题。 3、能根据具体问题的实际意义,检验结果是否合理。 过程与方法: 1、体验通过移动变化分析面积问题的方法。 发展学生应用数学的意思。 情感态度与价值观: 让学生体会一元二次方程是刻画现实世界一个有效的数学模型,感悟数学来源于生活,服务于生活;同时培养学生自我探索的兴趣和能力。 教学重点:运用一元二次方程探索和解决面积问题。 教学难点:面积问题中的等量分析
教 学 程 序 与 策 略
一:创设情境,引入新课提出问题:列方程解应用题的基本步骤有哪些?①审:审清题意:已知什么,求什么 已、未知之间有什么关系 ②设:设未知数,语句要完整,有单位(统一)的要注明单位;③列:列代数式,列方程;④解:解所列的方程;⑤验:是否是所列方程的根;是否符合题意;⑥答:答案也必需是完整的语句,注明单位.二:回顾问题1例1、在一块宽20m、长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把长方形空地分成大小一样的六块,建成小花坛。如图要使花坛的总面积为570 m2 ,问小路的宽应为多少?(回顾前面问题,引导学生解决)解:设小路宽x米。根据题意,得32×20-(32x+2×20x)+2x2=570整理得:x2-36x+35=0 得(x-1)(x-35)=0结合题意,x=35不可能,因此,只能取x=1.答:所求小路宽应为1m.议一议:还有其它的列法吗?试说明原因。(20-x)(32-2x)=570 平移(拼接)三:练一练在一块长16m,宽12m的长方形绿地上需要铺设若干条等宽的小路,若铺设小路后绿地的面积是140,请你根据以下方案分别求出小路的宽度。图一 图二四、例题讲解例4、正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20cm,容积为2880的口方盒。问金属片的边长是多少?问题:请你说说本题中的已知量和未知量 折叠前折叠后裁去小正方形边长20方盒的高20方盒的底面边长x-40正方形金属片的边长x方盒的底面积(x-40)2方盒的容积20(x-40)2解:设原金属片的边长为x cm。根据题意,得 20(x-40) = 2880解这个方程,得x=28不合题意,所以x=52答:原金属片的边长是52cm。五、练一练正方形金属片一块,将其四个角各截去一个边长为2cm的小正方形,围成容积为50cm3的开口方盒。问金属片的边长是多少?六、达标检测1、如图一,某小区一块长18m,宽6m的长方形空地,计划在其中修建两块相同的长方形绿地,它们的面积之和为60cm2,两块绿地之间及周边留有宽度相等的人行通道,若设人行道的宽度为x,则可以列出关于x的方程为 (不必化简)2、有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形
七、课堂小结: 提问:通过本堂课的学习,你学会了什么?列一元二次方程解应用题的一般步骤是:①审:审清题意:已知什么,求什么 已、未知之间有什么关系 ②设:设未知数,语句要完整,有单位(统一)的要注明单位;③列:列代数式,列方程;④解:解所列的方程;⑤验:是否是所列方程的根;是否符合题意;⑥答:答案也必需是完整的语句,注明单位且要贴近生活.
八、布置作业: 习题17.5第7题
九、教后反思
18m
6m
2 / 4
