2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理优生辅导测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理优生辅导测试题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 398.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:25:23 | ||
图片预览



文档简介
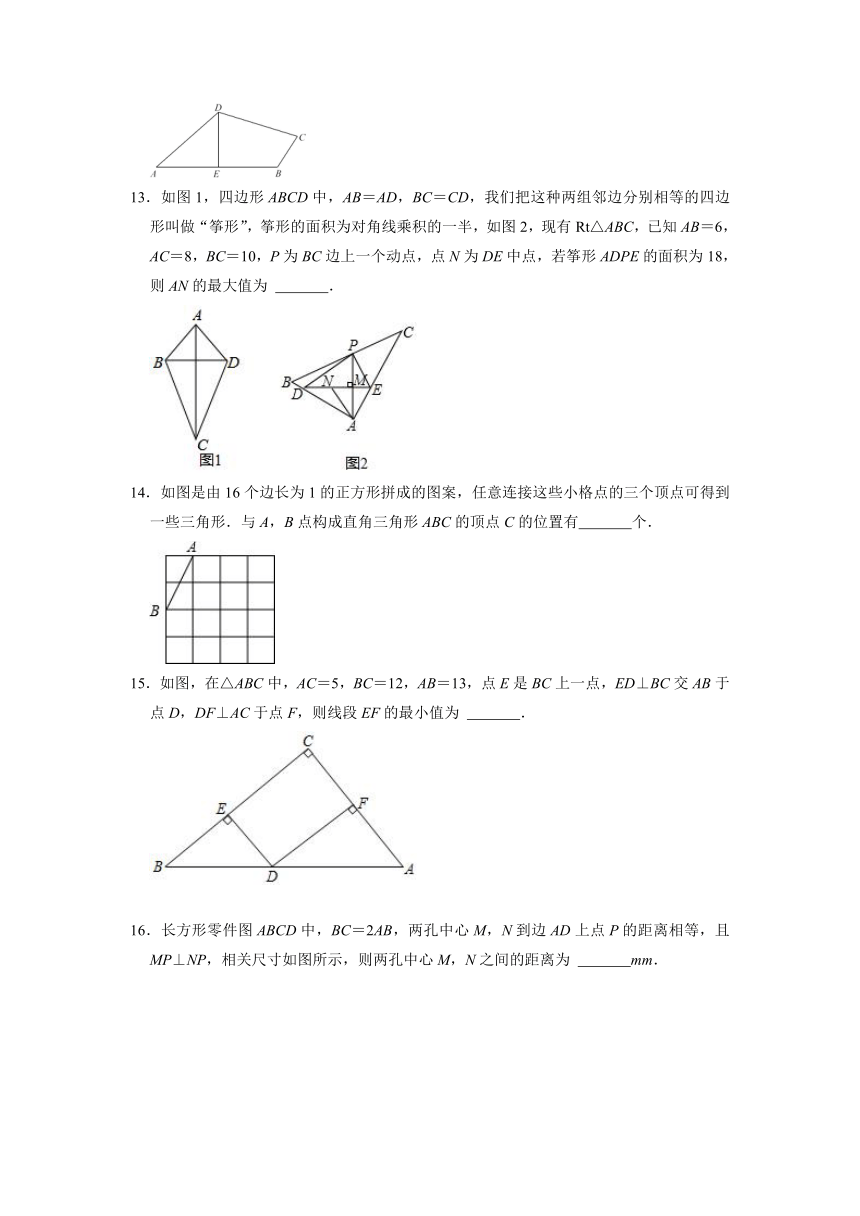
2021-2022学年人教版八年级数学下册《17-2勾股定理的逆定理》优生辅导测试题(附答案)
一.选择题(共8小题,满分32分)
1.下列条件中,不能判断△ABC为直角三角形的是( )
A.a=5,b=12,c=13 B.a:b:c=3:4:5
C.∠A+∠B=80° D.∠A:∠B:∠C=1:1:2
2.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
3.以下四组代数式作为△ABC的三边,能使△ABC为直角三角形的有( )
①3n,4n,5n(n为正整数);②n,n+1,n+2(n为正整数);③n2﹣1,2n,n2+1(n≥2,n为正整数);④m2﹣n2,2mn,m2+n2(m>n,m,n为正整数).
A.1组 B.2组 C.3组 D.4组
4.如图所示的网格是正方形网格,点A,B,C,D,E是网格线交点,则∠BAC﹣∠DAE的度数为( )
A.45° B.40° C.30° D.25°
5.如图,在单位为1的正方形网格图中有a,b,c,d四条线段,从中任取三条线段所构成的三角形中恰好是直角三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图,已知△ABC中,AB=10,AC=8,BC=6,AB的垂直平分线分别交AC,AB于D,E,连接BD,则CD的长为( )
A.1 B. C. D.
7.如图,车库宽AB的长为3米,一辆宽为1.8米(即MN=1.8米)的汽车正直停入车库(MN∥AB),车门CD长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门开至最大的宽度FG的长为( )
A.米 B.米 C.米 D.(﹣)米
8.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,∠B=90°,AB=8米,BC=6米.当正方形DEFH运动到什么位置,即当AE=( )米时,有DC2=AE2+BC2.
A.2 B.2.5 C.3.4 D.3.6
二.填空题(共8小题,满分32分)
9.探索勾股数的规律:
观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41)…可发现,4=,12=,24=…请写出第5个数组: .
10.如图,已知∠A=90°,AC=AB=3,CD=,BD=2,则点C到BD的距离为 .
11.已知在平面直角坐标系中A(﹣2,0)、B(2,0)、C(0,2).点P在x轴上运动,当点P与点A、B、C三点中任意两点构成直角三角形时,点P的坐标为 .
12.如图,在四边形ABCD中,E为AB的中点,DE⊥AB于点E,AB=8,DE=,BC=2,CD=5,则四边形ABCD的面积为 .
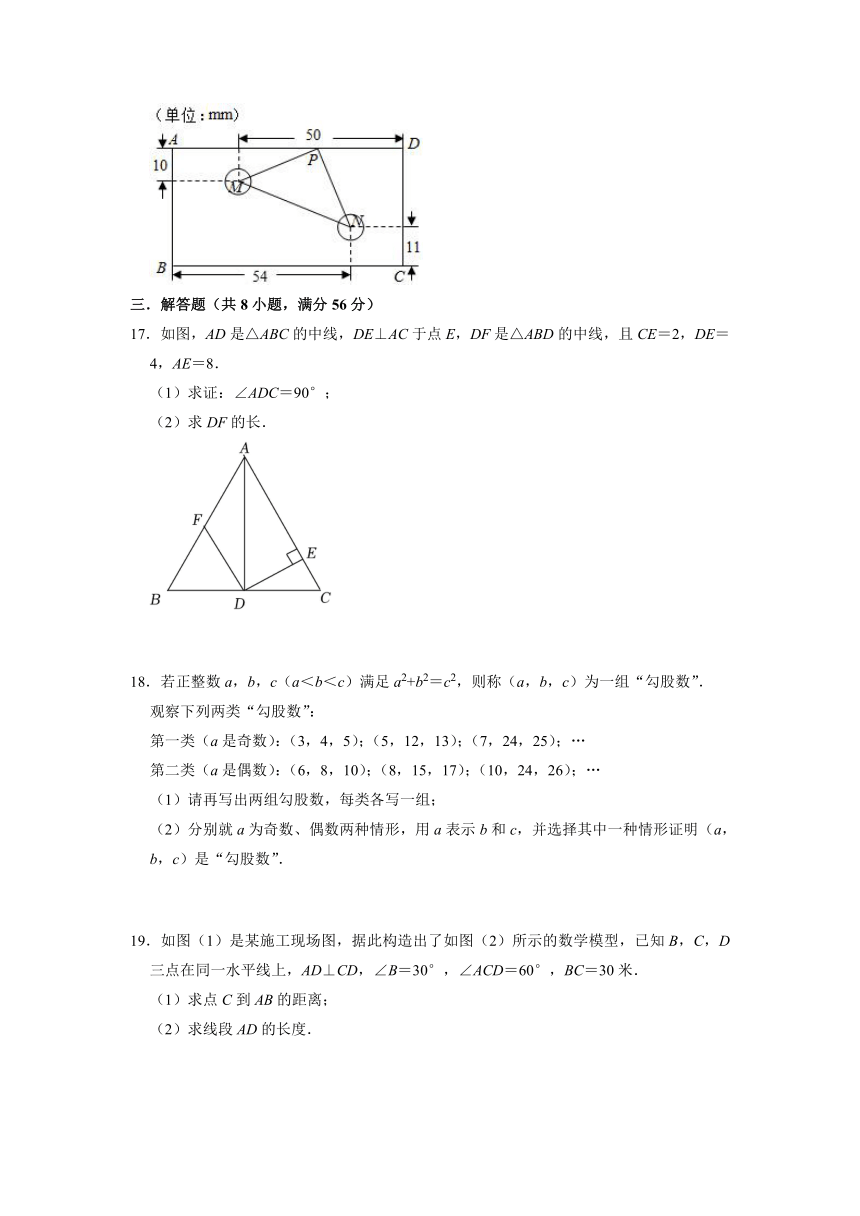
13.如图1,四边形ABCD中,AB=AD,BC=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”,筝形的面积为对角线乘积的一半,如图2,现有Rt△ABC,已知AB=6,AC=8,BC=10,P为BC边上一个动点,点N为DE中点,若筝形ADPE的面积为18,则AN的最大值为 .
14.如图是由16个边长为1的正方形拼成的图案,任意连接这些小格点的三个顶点可得到一些三角形.与A,B点构成直角三角形ABC的顶点C的位置有 个.
15.如图,在△ABC中,AC=5,BC=12,AB=13,点E是BC上一点,ED⊥BC交AB于点D,DF⊥AC于点F,则线段EF的最小值为 .
16.长方形零件图ABCD中,BC=2AB,两孔中心M,N到边AD上点P的距离相等,且MP⊥NP,相关尺寸如图所示,则两孔中心M,N之间的距离为 mm.
三.解答题(共8小题,满分56分)
17.如图,AD是△ABC的中线,DE⊥AC于点E,DF是△ABD的中线,且CE=2,DE=4,AE=8.
(1)求证:∠ADC=90°;
(2)求DF的长.
18.若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.
观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
19.如图(1)是某施工现场图,据此构造出了如图(2)所示的数学模型,已知B,C,D三点在同一水平线上,AD⊥CD,∠B=30°,∠ACD=60°,BC=30米.
(1)求点C到AB的距离;
(2)求线段AD的长度.
20.如图,小明家A和地铁口B两地恰好处在东西方向上,且相距3km,学校C在他家正北方向的4km处,公园D与地铁口和学校的距离分别5km和5km.
(1)求地铁口、公园和学校三地组成的∠BDC的大小;
(2)计算公园与小明家的距离.
21.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=8m,BC=17m,CD=9m,AD=12m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
22.如图,在四边形ABFC中,AC2=AB2+BC2,CD⊥AD,AD2=2AB2﹣CD2,连接EF.
(1)找出图中的所有直角三角形;
(2)求证:AB=BC.
23.在△ABC中,BC=a,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、10时,三角形为 三角形;当△ABC三边分别为6、8、9时,三角形为 三角形;当△ABC三边分别为6、8、11时,三角形为 三角形;
(2)猜想,当a2+b2 c2时;△ABC为锐角三角形;当a2+b2 c2时;△ABC为钝角三角形;
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
24.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形ADCG和长方形DEFC均为木质平台的横截面,点G在AB上,点C在GF上,点D在AE上,经过现场测量得知:CD=1米,AD=15米.
(1)小敏猜想立柱AB段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱AB段的正确长度;
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索BF,经测量DE=3米,请你求出要焊接的钢索BF的长.(结果不必化简成最简二次根式)
参考答案
一.选择题(共8小题,满分32分)
1.解:A.∵a=5,b=12,c=13,
∴a2+b2=52+122=25+144=169,c2=132=169,
∴a2+b2=c2,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵a:b:c=3:4:5,
∴a2+b2=c2,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵∠A+∠B=80°,
∴∠C=180°﹣(∠A+∠B)=100°>90°,
∴△ABC不是直角三角形,故本选项符合题意;
D.∵∠A:∠B:∠C=1:1:2,∠A+∠B+∠C=180°,
∴最大角∠C=180°=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:C.
2.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
3.解:①3n,4n,5n(n为正整数),(3n)2+(4n)2=(5n)2,能构成直角三角形;
②n,n+1,n+2(n为正整数),n2+(n+1)2≠(n+2)2,不能构成直角三角形;
③n2﹣1,2n,n2+1(n≥2,n为正整数),(n2﹣1)2+(n2+1)2=(2n)2,能构成直角三角形;
④m2﹣n2,2mn,m2+n2(m>n,m,n为正整数),(m2﹣n2)2+(2mn)2=(m2+n2)2,能构成直角三角形.
故选:C.
4.解:如图,连接CG、AG,
由勾股定理得:AC2=AG2=12+22=5,CG2=12+32=10,
∴AC2+AG2=CG2,
∴∠CAG=90°,
∴△CAG是等腰直角三角形,
∴∠ACG=45°,
∵CF∥AB,
∴∠ACF=∠BAC,
在△CFG和△ADE中,
,
∴△CFG≌△ADE(SAS),
∴∠FCG=∠DAE,
∴∠BAC﹣∠DAE=∠ACF﹣∠FCG=∠ACG=45°,
故选:A.
5.解:由图可得,
线段a,b,c,d的长度分别为:,3,2,,
∵()2+(2)2=()2,()2+(2)2=(3)2,
∴从a,b,c,d四条线段中任取三条线段所构成的三角形中恰好是直角三角形的个数为2,
故选:B.
6.解:∵△ABC中,AB=10,AC=8,BC=6,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∵AB的垂直平分线分别交AC,AB于D,E,
∴AD=DB,
设CD为x,AD=DB=8﹣x,
在Rt△CDB中,CD2+BC2=DB2,
即x2+62=(8﹣x)2,
解得:x=,
即CD=,
故选:C.
7.解:如图所示,过C作CO⊥DE于O,
∵∠CDE=45°,CD=,
∴CO=CD cos∠CDE=,
∵AB=MN+CO+FG,
∴FG=3﹣1.8﹣=,
故选:D.
8.解:如图,连接CD,
∵∠B=90°,AB=8,BC=6,
∴AC=10,
假设AE=x,可得EC=10﹣x.
∵正方形DEFH的边长为2,即DE=2,
∴DC2=DE2+EC2=22+(10﹣x)2,
AE2+BC2=x2+36,
∵DC2=AE2+BC2,
∴4+(10﹣x)2=x2+36,
解得:x=3.4,
所以,当AE=3.4米时,有DC2=AE2+BC2.
故选:C.
二.填空题(共8小题,满分32分)
9.解:∵①3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
②5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
③7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
④9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
⑤11=2×5+1,60=2×52+2×5,61=2×52+2×5+1,
故答案为:11,60,61.
10.解:∵∠A=90°,AC=AB=3,
∴BC===3,
∵CD=,BD=2,
()2+(3)2=(2)2,
∴△BCD是直角三角形,
∴点C到BD的距离为×3÷2×2÷2=.
故答案为:.
11.解:∵点P、A、B在x轴上,
∴P、A、B三点不能构成三角形.
设点P的坐标为(m,0).
当△PAC为直角三角形时,
①∠APC=90°,易知点P在原点处坐标为(0,0);
②∠ACP=90°时,如图,
∵∠ACP=90°
∴AC2+PC2=AP2,
,
解得,m=,
∴点P的坐标为(,0);
当△PBC为直角三角形时,
①∠BPC=90°,易知点P在原点处坐标为(0,0);
②∠BCP=90°时,
∵∠BCP=90°,CO⊥PB,
∴PO=BO=2,
∴点P的坐标为(﹣2,0).
综上所述点P的坐标为(0,0),(,0),(﹣2,0).
12.解:连接BD,
∵E为AB的中点,DE⊥AB,AB=8,
∴AE=BE=4,∠DEB=90°,
∵DE=,
∴BD===,
∵BC=2,CD=5,
∴BD2+BC2=CD2,
∴△DBC是直角三角形(∠DBC=90°),
∴四边形ABCD的面积S=S△DAB+S△DBC
=+
=+×2
=4+,
故答案为:4+.
13.解:如图,
∵ADPE是筝形,
∴S四边形ADPE==18,
∴AP DE=18,
当AP取最小值时,DE有最大值,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=100,BC2=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∵P为BC边上的一个动点,
∴当AP⊥BC时,AP取到最小值,
∴AP的最小值为:===,
∴=36,
∴DE=,
在Rt△ADE中,点N为DE的中点,
∴AN=,
∴当DE取最大值时,AN有最大值,
∴AN的最大值为,
故答案为.
14.解:如图所示:
当∠C为直角顶点时,有C1,C2两点;
当∠A为直角顶点时,有C3一点;
当∠B为直角顶点时,有C4,C5两点,
综上所述,共有5个点.
故答案为:5.
15.解:连接CD,EF,
∵AC=5,BC=12,AB=13,
∴AC2+BC2=52+122=169,AB2=132=169,
∴BC2+AC2=AB2,
∴∠BCA=90°,
∵DE⊥CB,DF⊥AC,
∴四边形DECF是矩形,
∴EF=CD,
∴当CD值最小时,EF的值最小,
∴根据垂线段最短,则当CD⊥BA时,CD的值最小,
此时,∵S△ABC=BC AC=AB CD,
∴CD===,
∴EF的最小值为,
故答案为.
16.解:如图,过M作ME⊥AD于E,过N作NF⊥AD于F,
则∠MEP=∠NFP=90°,
∵MP⊥NP,
∴∠MPN=90°,
∴∠PME+∠MPE=∠MPE+∠NPF=90°,
∴∠EMP=∠NPF,
∵PM=PN,
∴△PEM≌△NFP(AAS),
∴PF=EM=10mm,PE=FN,
设PE=FN=x,
∴CD=(11+x)mm,DF=(50﹣x﹣10)mm,
∴BC=(54+50﹣x﹣10)=94﹣x (mm),
∵四边形ABCD是矩形,
∴CD=AB,
∵BC=2AB,
∴54+50﹣x﹣10=2(11+x),
解得:x=24,
∴PE=FN=24mm,
∵EM=10mm,
∴PM===26(mm),
∴MN===26(mm),
答:两孔中心M,N之间的距离为26mm,
故答案为:26.
三.解答题(共8小题,满分56分)
17.证明:(1)∵DE⊥AC于点E,
∴∠AED=∠CED=90°,
在Rt△ADE中,∠AED=90°,
∴AD2=AE2+DE2=82+42=80,
同理:CD2=20,
∴AD2+CD2=100,
∵AC=AE+CE=8+2=10,
∴AC2=100,
∴AD2+CD2=AC2,
∴△ADC是直角三角形,
∴∠ADC=90°;
(2)∵AD是△ABC的中线,∠ADC=90°,
∴AD垂直平分BC,
∴AB=AC=10,
在Rt△ADB中,∠ADB=90°,
∵点F是边AB的中点,
∴DF=.
18.解:(1)第一组(a是奇数):9,40,41(答案不唯一);
第二组(a是偶数):12,35,37(答案不唯一);
(2)当a为奇数时,,;
当a为偶数时,,;
证明:当a为奇数时,a2+b2=,
∴(a,b,c)是“勾股数”.
当a为偶数时,a2+b2=
∴(a,b,c)是“勾股数”.
19.解:(1)过点C作CE⊥AB于点E,
∴∠CEB=90°,
∵∠B=30°,BC=30米,
∴CE=BC=15(米)
∴点C到AB的距离是15米;
(2)∵AD⊥CD,
∴∠ADC=90°,
∵∠ACD=60°,∠B=30°,
∴∠CAD=90°﹣∠ACD=30°,∠BAC=∠ACD﹣∠B=30°,
∴∠CAD=∠BAC,
∵CE⊥AB,
∴CD=CE=15米,
在Rt△ACD中,∠CAD=30°,CD=15米,
∴CD=AC,
∴AC=CD=2×15=30(米),
由勾股定理得:AD===15(米),
答:线段AD的长度是15米.
20.解:(1)由题意得:BD=5km,CD=5km,∠BAC=90°,AB=3km,CA=4km,
∴BC===5(km),
∴BC=BD,
∵BC2+BD2=52+52=50,CD2=(5)2=50,
∴BC2+BD2=CD2,
∴△BCD是等腰直角三角形,∠CBD=90°,
∴∠BDC=45°;
(2)过D作DE⊥AB,交AB的延长线于E,如图所示:
则∠DEB=90°,
∴∠BDE+∠DBE=90°,
由(1)得:∠CBD=90°,
∴∠DBE+∠CBA=90°,
∴∠BDE=∠CBA,
在△BDE和△CBA中,
,
∴△BDE≌△CBA(AAS),
∴DE=BA=3km,BE=CA=4km,
∴AE=BE+AB=7(km),
∴AD===(km).
21.解:(1)∵AB⊥AC,
∴∠BAC=90°,
∴AC===15(m),
∵CD=9m,AD=12m,
∴AD2+CD2=122+92=225=AC2,
∴△ACD是直角三角形,∠D=90°,
∴需要绿化的空地ABCD的面积=S△ABC+S△ACD=AB×AC+AD×CD=×8×15+×12×9=114(m2);
(2)∵∠BAC=90°,AE⊥BC,
∴S△ABC=BC×AE=AB AC,
∴17×AE=8×15,
解得:AE=(m),
即小路AE的长为m.
22.解:(1)∵AC2=AB2+BC2,
∴△ABC是直角三角形,
∵CD⊥AD,
∴△ADC,△EDC,△EDF,△ABC,△ABE是直角三角形;
(2)∵AC2=AB2+BC2,AD2=2AB2﹣CD2,
∵△ADC是直角三角形,
∴AC2=AD2+DC2,
∴AB2+BC2=AD2+DC2,
∴AB2+BC2=2AB2﹣DC2+DC2
即AB2=BC2,
∴AB=BC.
23.解:(1)当△ABC三边分别为6、8、10时,62+82=102,△ABC为直角三角形;
当△ABC三边分别为6、8、9时,△ABC为锐角三角形;
当△ABC三边分别为6、8、11时,△ABC为钝角三角形;
故答案为:直角;锐角;钝角;
(2)当a2+b2>c2时,△ABC为锐角三角形;
当a2+b2<c2时,△ABC为钝角三角形;
故答案为:>;<;
(3)∵c为最长边,2+4=6,
∴4≤c<6,
a2+b2=22+42=20,
①a2+b2>c2,即c2<20,0<c<2,
∴当4≤c<2时,这个三角形是锐角三角形;
②a2+b2=c2,即c2=20,c=2,
∴当c=2时,这个三角形是直角三角形;
③a2+b2<c2,即c2>20,c>2,
∴当2<c<6时,这个三角形是钝角三角形.
24.解:(1)不正确,理由如下:
由题意得:AG=CD=1米,GC=AD=15米,
设BG=x米,则BC=(26﹣1﹣x)米,
在Rt△BGC中,由勾股定理得:BG2+CG2=CB2,
即x2+152=(26﹣1﹣x)2,
解得:x=8,
∴BG=8米,
∴AB=BG+GA=9(米),
∴小敏的猜想不正确,立柱AB段的正确长度长为9米.
(2)由题意得:CF=DE=3米,
∴GF=GC+CF=18(米),
在Rt△BGF中,由勾股定理得:BF===(米).
一.选择题(共8小题,满分32分)
1.下列条件中,不能判断△ABC为直角三角形的是( )
A.a=5,b=12,c=13 B.a:b:c=3:4:5
C.∠A+∠B=80° D.∠A:∠B:∠C=1:1:2
2.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
3.以下四组代数式作为△ABC的三边,能使△ABC为直角三角形的有( )
①3n,4n,5n(n为正整数);②n,n+1,n+2(n为正整数);③n2﹣1,2n,n2+1(n≥2,n为正整数);④m2﹣n2,2mn,m2+n2(m>n,m,n为正整数).
A.1组 B.2组 C.3组 D.4组
4.如图所示的网格是正方形网格,点A,B,C,D,E是网格线交点,则∠BAC﹣∠DAE的度数为( )
A.45° B.40° C.30° D.25°
5.如图,在单位为1的正方形网格图中有a,b,c,d四条线段,从中任取三条线段所构成的三角形中恰好是直角三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图,已知△ABC中,AB=10,AC=8,BC=6,AB的垂直平分线分别交AC,AB于D,E,连接BD,则CD的长为( )
A.1 B. C. D.
7.如图,车库宽AB的长为3米,一辆宽为1.8米(即MN=1.8米)的汽车正直停入车库(MN∥AB),车门CD长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门开至最大的宽度FG的长为( )
A.米 B.米 C.米 D.(﹣)米
8.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,∠B=90°,AB=8米,BC=6米.当正方形DEFH运动到什么位置,即当AE=( )米时,有DC2=AE2+BC2.
A.2 B.2.5 C.3.4 D.3.6
二.填空题(共8小题,满分32分)
9.探索勾股数的规律:
观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41)…可发现,4=,12=,24=…请写出第5个数组: .
10.如图,已知∠A=90°,AC=AB=3,CD=,BD=2,则点C到BD的距离为 .
11.已知在平面直角坐标系中A(﹣2,0)、B(2,0)、C(0,2).点P在x轴上运动,当点P与点A、B、C三点中任意两点构成直角三角形时,点P的坐标为 .
12.如图,在四边形ABCD中,E为AB的中点,DE⊥AB于点E,AB=8,DE=,BC=2,CD=5,则四边形ABCD的面积为 .
13.如图1,四边形ABCD中,AB=AD,BC=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”,筝形的面积为对角线乘积的一半,如图2,现有Rt△ABC,已知AB=6,AC=8,BC=10,P为BC边上一个动点,点N为DE中点,若筝形ADPE的面积为18,则AN的最大值为 .
14.如图是由16个边长为1的正方形拼成的图案,任意连接这些小格点的三个顶点可得到一些三角形.与A,B点构成直角三角形ABC的顶点C的位置有 个.
15.如图,在△ABC中,AC=5,BC=12,AB=13,点E是BC上一点,ED⊥BC交AB于点D,DF⊥AC于点F,则线段EF的最小值为 .
16.长方形零件图ABCD中,BC=2AB,两孔中心M,N到边AD上点P的距离相等,且MP⊥NP,相关尺寸如图所示,则两孔中心M,N之间的距离为 mm.
三.解答题(共8小题,满分56分)
17.如图,AD是△ABC的中线,DE⊥AC于点E,DF是△ABD的中线,且CE=2,DE=4,AE=8.
(1)求证:∠ADC=90°;
(2)求DF的长.
18.若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.
观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
19.如图(1)是某施工现场图,据此构造出了如图(2)所示的数学模型,已知B,C,D三点在同一水平线上,AD⊥CD,∠B=30°,∠ACD=60°,BC=30米.
(1)求点C到AB的距离;
(2)求线段AD的长度.
20.如图,小明家A和地铁口B两地恰好处在东西方向上,且相距3km,学校C在他家正北方向的4km处,公园D与地铁口和学校的距离分别5km和5km.
(1)求地铁口、公园和学校三地组成的∠BDC的大小;
(2)计算公园与小明家的距离.
21.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=8m,BC=17m,CD=9m,AD=12m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
22.如图,在四边形ABFC中,AC2=AB2+BC2,CD⊥AD,AD2=2AB2﹣CD2,连接EF.
(1)找出图中的所有直角三角形;
(2)求证:AB=BC.
23.在△ABC中,BC=a,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、10时,三角形为 三角形;当△ABC三边分别为6、8、9时,三角形为 三角形;当△ABC三边分别为6、8、11时,三角形为 三角形;
(2)猜想,当a2+b2 c2时;△ABC为锐角三角形;当a2+b2 c2时;△ABC为钝角三角形;
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
24.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形ADCG和长方形DEFC均为木质平台的横截面,点G在AB上,点C在GF上,点D在AE上,经过现场测量得知:CD=1米,AD=15米.
(1)小敏猜想立柱AB段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱AB段的正确长度;
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索BF,经测量DE=3米,请你求出要焊接的钢索BF的长.(结果不必化简成最简二次根式)
参考答案
一.选择题(共8小题,满分32分)
1.解:A.∵a=5,b=12,c=13,
∴a2+b2=52+122=25+144=169,c2=132=169,
∴a2+b2=c2,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵a:b:c=3:4:5,
∴a2+b2=c2,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵∠A+∠B=80°,
∴∠C=180°﹣(∠A+∠B)=100°>90°,
∴△ABC不是直角三角形,故本选项符合题意;
D.∵∠A:∠B:∠C=1:1:2,∠A+∠B+∠C=180°,
∴最大角∠C=180°=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:C.
2.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
3.解:①3n,4n,5n(n为正整数),(3n)2+(4n)2=(5n)2,能构成直角三角形;
②n,n+1,n+2(n为正整数),n2+(n+1)2≠(n+2)2,不能构成直角三角形;
③n2﹣1,2n,n2+1(n≥2,n为正整数),(n2﹣1)2+(n2+1)2=(2n)2,能构成直角三角形;
④m2﹣n2,2mn,m2+n2(m>n,m,n为正整数),(m2﹣n2)2+(2mn)2=(m2+n2)2,能构成直角三角形.
故选:C.
4.解:如图,连接CG、AG,
由勾股定理得:AC2=AG2=12+22=5,CG2=12+32=10,
∴AC2+AG2=CG2,
∴∠CAG=90°,
∴△CAG是等腰直角三角形,
∴∠ACG=45°,
∵CF∥AB,
∴∠ACF=∠BAC,
在△CFG和△ADE中,
,
∴△CFG≌△ADE(SAS),
∴∠FCG=∠DAE,
∴∠BAC﹣∠DAE=∠ACF﹣∠FCG=∠ACG=45°,
故选:A.
5.解:由图可得,
线段a,b,c,d的长度分别为:,3,2,,
∵()2+(2)2=()2,()2+(2)2=(3)2,
∴从a,b,c,d四条线段中任取三条线段所构成的三角形中恰好是直角三角形的个数为2,
故选:B.
6.解:∵△ABC中,AB=10,AC=8,BC=6,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∵AB的垂直平分线分别交AC,AB于D,E,
∴AD=DB,
设CD为x,AD=DB=8﹣x,
在Rt△CDB中,CD2+BC2=DB2,
即x2+62=(8﹣x)2,
解得:x=,
即CD=,
故选:C.
7.解:如图所示,过C作CO⊥DE于O,
∵∠CDE=45°,CD=,
∴CO=CD cos∠CDE=,
∵AB=MN+CO+FG,
∴FG=3﹣1.8﹣=,
故选:D.
8.解:如图,连接CD,
∵∠B=90°,AB=8,BC=6,
∴AC=10,
假设AE=x,可得EC=10﹣x.
∵正方形DEFH的边长为2,即DE=2,
∴DC2=DE2+EC2=22+(10﹣x)2,
AE2+BC2=x2+36,
∵DC2=AE2+BC2,
∴4+(10﹣x)2=x2+36,
解得:x=3.4,
所以,当AE=3.4米时,有DC2=AE2+BC2.
故选:C.
二.填空题(共8小题,满分32分)
9.解:∵①3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
②5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
③7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
④9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
⑤11=2×5+1,60=2×52+2×5,61=2×52+2×5+1,
故答案为:11,60,61.
10.解:∵∠A=90°,AC=AB=3,
∴BC===3,
∵CD=,BD=2,
()2+(3)2=(2)2,
∴△BCD是直角三角形,
∴点C到BD的距离为×3÷2×2÷2=.
故答案为:.
11.解:∵点P、A、B在x轴上,
∴P、A、B三点不能构成三角形.
设点P的坐标为(m,0).
当△PAC为直角三角形时,
①∠APC=90°,易知点P在原点处坐标为(0,0);
②∠ACP=90°时,如图,
∵∠ACP=90°
∴AC2+PC2=AP2,
,
解得,m=,
∴点P的坐标为(,0);
当△PBC为直角三角形时,
①∠BPC=90°,易知点P在原点处坐标为(0,0);
②∠BCP=90°时,
∵∠BCP=90°,CO⊥PB,
∴PO=BO=2,
∴点P的坐标为(﹣2,0).
综上所述点P的坐标为(0,0),(,0),(﹣2,0).
12.解:连接BD,
∵E为AB的中点,DE⊥AB,AB=8,
∴AE=BE=4,∠DEB=90°,
∵DE=,
∴BD===,
∵BC=2,CD=5,
∴BD2+BC2=CD2,
∴△DBC是直角三角形(∠DBC=90°),
∴四边形ABCD的面积S=S△DAB+S△DBC
=+
=+×2
=4+,
故答案为:4+.
13.解:如图,
∵ADPE是筝形,
∴S四边形ADPE==18,
∴AP DE=18,
当AP取最小值时,DE有最大值,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=100,BC2=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∵P为BC边上的一个动点,
∴当AP⊥BC时,AP取到最小值,
∴AP的最小值为:===,
∴=36,
∴DE=,
在Rt△ADE中,点N为DE的中点,
∴AN=,
∴当DE取最大值时,AN有最大值,
∴AN的最大值为,
故答案为.
14.解:如图所示:
当∠C为直角顶点时,有C1,C2两点;
当∠A为直角顶点时,有C3一点;
当∠B为直角顶点时,有C4,C5两点,
综上所述,共有5个点.
故答案为:5.
15.解:连接CD,EF,
∵AC=5,BC=12,AB=13,
∴AC2+BC2=52+122=169,AB2=132=169,
∴BC2+AC2=AB2,
∴∠BCA=90°,
∵DE⊥CB,DF⊥AC,
∴四边形DECF是矩形,
∴EF=CD,
∴当CD值最小时,EF的值最小,
∴根据垂线段最短,则当CD⊥BA时,CD的值最小,
此时,∵S△ABC=BC AC=AB CD,
∴CD===,
∴EF的最小值为,
故答案为.
16.解:如图,过M作ME⊥AD于E,过N作NF⊥AD于F,
则∠MEP=∠NFP=90°,
∵MP⊥NP,
∴∠MPN=90°,
∴∠PME+∠MPE=∠MPE+∠NPF=90°,
∴∠EMP=∠NPF,
∵PM=PN,
∴△PEM≌△NFP(AAS),
∴PF=EM=10mm,PE=FN,
设PE=FN=x,
∴CD=(11+x)mm,DF=(50﹣x﹣10)mm,
∴BC=(54+50﹣x﹣10)=94﹣x (mm),
∵四边形ABCD是矩形,
∴CD=AB,
∵BC=2AB,
∴54+50﹣x﹣10=2(11+x),
解得:x=24,
∴PE=FN=24mm,
∵EM=10mm,
∴PM===26(mm),
∴MN===26(mm),
答:两孔中心M,N之间的距离为26mm,
故答案为:26.
三.解答题(共8小题,满分56分)
17.证明:(1)∵DE⊥AC于点E,
∴∠AED=∠CED=90°,
在Rt△ADE中,∠AED=90°,
∴AD2=AE2+DE2=82+42=80,
同理:CD2=20,
∴AD2+CD2=100,
∵AC=AE+CE=8+2=10,
∴AC2=100,
∴AD2+CD2=AC2,
∴△ADC是直角三角形,
∴∠ADC=90°;
(2)∵AD是△ABC的中线,∠ADC=90°,
∴AD垂直平分BC,
∴AB=AC=10,
在Rt△ADB中,∠ADB=90°,
∵点F是边AB的中点,
∴DF=.
18.解:(1)第一组(a是奇数):9,40,41(答案不唯一);
第二组(a是偶数):12,35,37(答案不唯一);
(2)当a为奇数时,,;
当a为偶数时,,;
证明:当a为奇数时,a2+b2=,
∴(a,b,c)是“勾股数”.
当a为偶数时,a2+b2=
∴(a,b,c)是“勾股数”.
19.解:(1)过点C作CE⊥AB于点E,
∴∠CEB=90°,
∵∠B=30°,BC=30米,
∴CE=BC=15(米)
∴点C到AB的距离是15米;
(2)∵AD⊥CD,
∴∠ADC=90°,
∵∠ACD=60°,∠B=30°,
∴∠CAD=90°﹣∠ACD=30°,∠BAC=∠ACD﹣∠B=30°,
∴∠CAD=∠BAC,
∵CE⊥AB,
∴CD=CE=15米,
在Rt△ACD中,∠CAD=30°,CD=15米,
∴CD=AC,
∴AC=CD=2×15=30(米),
由勾股定理得:AD===15(米),
答:线段AD的长度是15米.
20.解:(1)由题意得:BD=5km,CD=5km,∠BAC=90°,AB=3km,CA=4km,
∴BC===5(km),
∴BC=BD,
∵BC2+BD2=52+52=50,CD2=(5)2=50,
∴BC2+BD2=CD2,
∴△BCD是等腰直角三角形,∠CBD=90°,
∴∠BDC=45°;
(2)过D作DE⊥AB,交AB的延长线于E,如图所示:
则∠DEB=90°,
∴∠BDE+∠DBE=90°,
由(1)得:∠CBD=90°,
∴∠DBE+∠CBA=90°,
∴∠BDE=∠CBA,
在△BDE和△CBA中,
,
∴△BDE≌△CBA(AAS),
∴DE=BA=3km,BE=CA=4km,
∴AE=BE+AB=7(km),
∴AD===(km).
21.解:(1)∵AB⊥AC,
∴∠BAC=90°,
∴AC===15(m),
∵CD=9m,AD=12m,
∴AD2+CD2=122+92=225=AC2,
∴△ACD是直角三角形,∠D=90°,
∴需要绿化的空地ABCD的面积=S△ABC+S△ACD=AB×AC+AD×CD=×8×15+×12×9=114(m2);
(2)∵∠BAC=90°,AE⊥BC,
∴S△ABC=BC×AE=AB AC,
∴17×AE=8×15,
解得:AE=(m),
即小路AE的长为m.
22.解:(1)∵AC2=AB2+BC2,
∴△ABC是直角三角形,
∵CD⊥AD,
∴△ADC,△EDC,△EDF,△ABC,△ABE是直角三角形;
(2)∵AC2=AB2+BC2,AD2=2AB2﹣CD2,
∵△ADC是直角三角形,
∴AC2=AD2+DC2,
∴AB2+BC2=AD2+DC2,
∴AB2+BC2=2AB2﹣DC2+DC2
即AB2=BC2,
∴AB=BC.
23.解:(1)当△ABC三边分别为6、8、10时,62+82=102,△ABC为直角三角形;
当△ABC三边分别为6、8、9时,△ABC为锐角三角形;
当△ABC三边分别为6、8、11时,△ABC为钝角三角形;
故答案为:直角;锐角;钝角;
(2)当a2+b2>c2时,△ABC为锐角三角形;
当a2+b2<c2时,△ABC为钝角三角形;
故答案为:>;<;
(3)∵c为最长边,2+4=6,
∴4≤c<6,
a2+b2=22+42=20,
①a2+b2>c2,即c2<20,0<c<2,
∴当4≤c<2时,这个三角形是锐角三角形;
②a2+b2=c2,即c2=20,c=2,
∴当c=2时,这个三角形是直角三角形;
③a2+b2<c2,即c2>20,c>2,
∴当2<c<6时,这个三角形是钝角三角形.
24.解:(1)不正确,理由如下:
由题意得:AG=CD=1米,GC=AD=15米,
设BG=x米,则BC=(26﹣1﹣x)米,
在Rt△BGC中,由勾股定理得:BG2+CG2=CB2,
即x2+152=(26﹣1﹣x)2,
解得:x=8,
∴BG=8米,
∴AB=BG+GA=9(米),
∴小敏的猜想不正确,立柱AB段的正确长度长为9米.
(2)由题意得:CF=DE=3米,
∴GF=GC+CF=18(米),
在Rt△BGF中,由勾股定理得:BF===(米).
