苏科版数学七下7.1.1探索直线平行的条件 课件(共24张PPT)
文档属性
| 名称 | 苏科版数学七下7.1.1探索直线平行的条件 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
7.1探索直线平行的条件(1)
1.会正确识别同位角、内错角、同旁内角.
2.探索基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
3.通过探索直线平行条件的过程,发展空间观念和有条理的表达能力.
学习目标
邻补角的概念:
对顶角的概念:
对顶角的性质:
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。
对顶角相等。
1
2
3
4
O
D
A
B
C
知识点回顾
∠1与∠3, ∠2与∠3,∠2与∠4,∠4与∠1
∠1与∠2, ∠3与∠4
∠1=∠2, ∠3=∠4
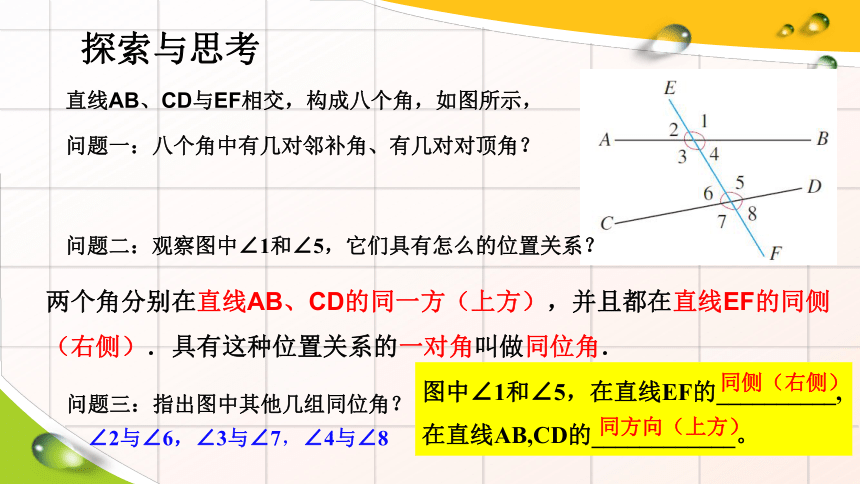
直线AB、CD与EF相交,构成八个角,如图所示,
问题一:八个角中有几对邻补角、有几对对顶角?
探索与思考
问题二:观察图中∠1和∠5,它们具有怎么的位置关系?
两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同侧(右侧).具有这种位置关系的一对角叫做同位角.
问题三:指出图中其他几组同位角?
∠2与∠6,∠3与∠7,∠4与∠8
图中∠1和∠5,在直线EF的__________,
在直线AB,CD的____________。
同侧(右侧)
同方向(上方)
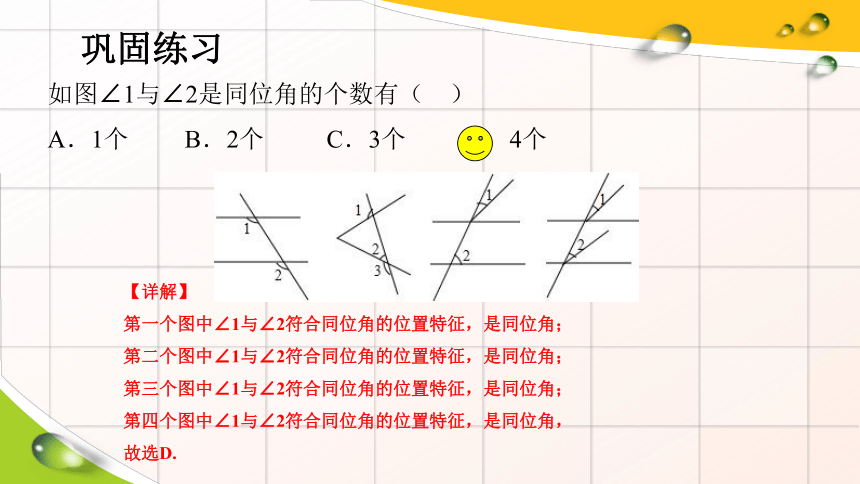
如图∠1与∠2是同位角的个数有( )
A.1个 B.2个 C.3个 D.4个
【详解】
第一个图中∠1与∠2符合同位角的位置特征,是同位角;
第二个图中∠1与∠2符合同位角的位置特征,是同位角;
第三个图中∠1与∠2符合同位角的位置特征,是同位角;
第四个图中∠1与∠2符合同位角的位置特征,是同位角,
故选D.
巩固练习
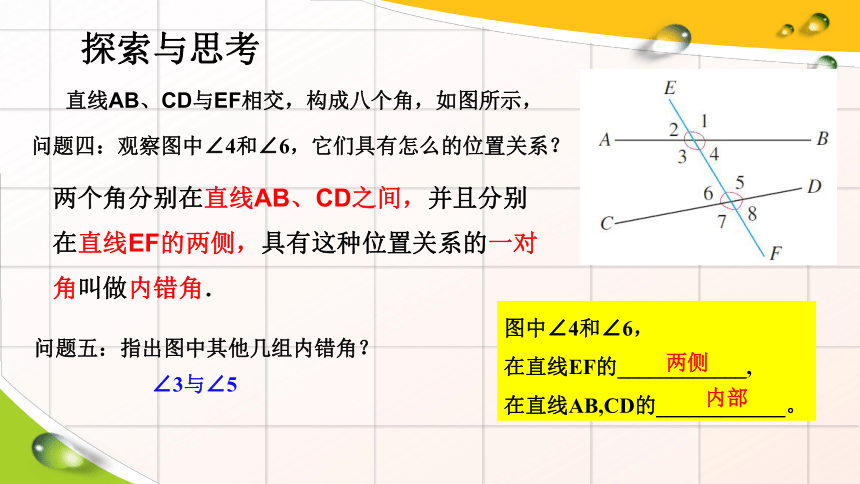
直线AB、CD与EF相交,构成八个角,如图所示,
问题四:观察图中∠4和∠6,它们具有怎么的位置关系?
探索与思考
问题五:指出图中其他几组内错角?
两个角分别在直线AB、CD之间,并且分别在直线EF的两侧,具有这种位置关系的一对角叫做内错角.
∠3与∠5
图中∠4和∠6,
在直线EF的____________,
在直线AB,CD的____________。
两侧
内部
如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B.内错角 C.对顶角 D.同旁内角
【详解】
两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是内错角.故选B.
巩固练习
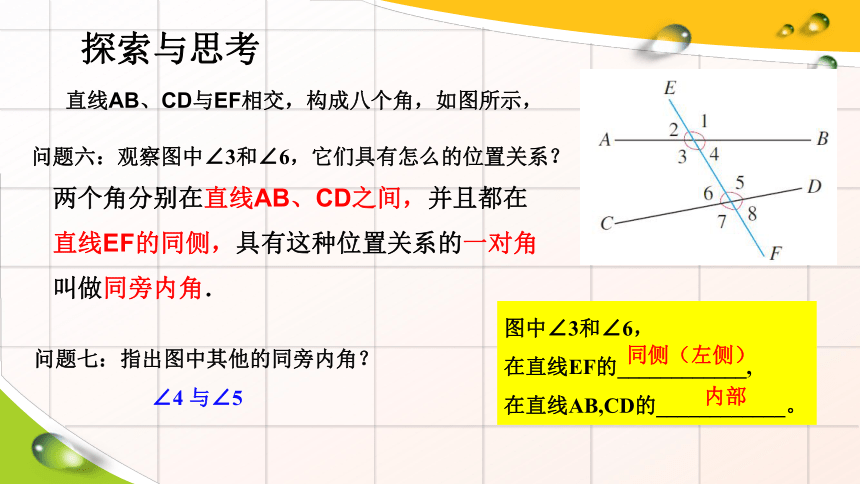
直线AB、CD与EF相交,构成八个角,如图所示,
问题六:观察图中∠3和∠6,它们具有怎么的位置关系?
探索与思考
问题七:指出图中其他的同旁内角?
两个角分别在直线AB、CD之间,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同旁内角.
∠4 与∠5
图中∠3和∠6,
在直线EF的____________,
在直线AB,CD的____________。
同侧(左侧)
内部
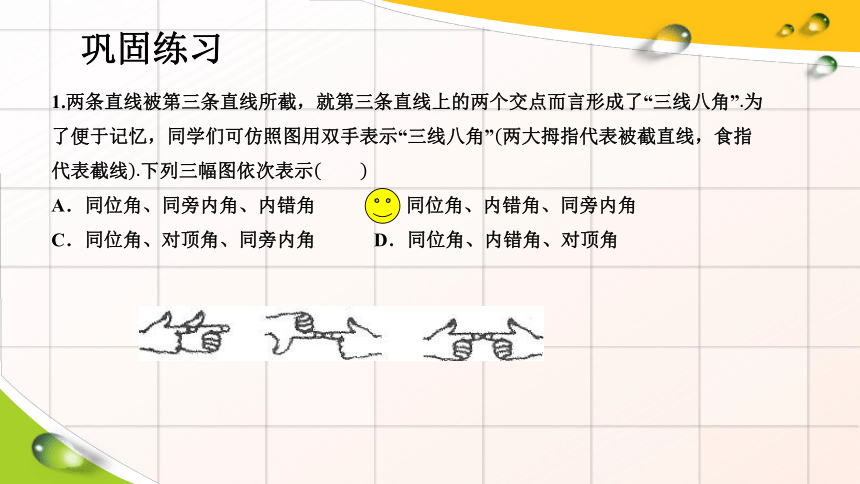
1.两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆,同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线,食指代表截线下列三幅图依次表示
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
巩固练习
2.如图,描述同位角、内错角、同旁内角关系不正确的是()
A.与∠4是同位角 B.与是内错角
C.与∠4是同旁内角 D.与∠4是同旁内角
【解析】
解:A.∠1与∠4是同位角,故A选项正确;
B.∠2与∠3是内错角,故B选项正确;
C.∠3与∠4是同旁内角,故C选项正确;
D.∠2与∠4是同旁内角,故D选项错误.
故选D.
巩固练习
3.如图,下列说法一定正确的是( )
A.∠1和∠4是内错角 B.∠1和∠3是同位角
C.∠3和∠4是同旁内角 D.∠1和∠C是同位角
【详解】
解:A、∠2和∠4是内错角,故本选项错误;
B、∠1和∠C是同位角,故本选项错误;
C、∠3和∠4是邻补角,故本选项错误;
D、∠1和∠C是同位角,故本选项正确;
故选:D.
巩固练面内两直线有何位置关系?
c
a
a
b
同一平面内,不相交的两条直线叫做平行线。
a
b
平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”。
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a。
平行线的概念:
表示方法:
知识点回顾
平行线的性质(平行公理):
·
P
a
b
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
a
b
c
几何语言表达式:
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:
∵ a∥b, b∥c (已知)
∴ a∥c (平行线的传递性)
知识点回顾
你能画出一条直线的平行线吗?
已知直线a,你能画出直线a的平行线吗?
a
b
平行线的画法 :一放、二靠、三推、四画。
观察∠1与∠2,你发现了什么?
P
a
b
c
1
2
A
B
P
画直线a的平行线b,实际就是过P点画与∠2相等的∠1,而∠1与∠2正是a,b被直线c截得同位角。
若同位角相等,则a∥b
探索新知
基本事实:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
几何语言:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
探索新知
你能说出木工用角尺画平行线的道理吗?
a
b
1
2
同位角相等,两直线平行
联系实际
如图,a、b、c、d是直线,E、F、G、H是交点,
(1)若∠1=∠2,可以证明______∥______,这是因为∠1和∠2是直线_______和_____被直线____所截而成的____________.
(2)若∠1=∠3,可以证明______∥______,这是因为∠1和∠3是直线______和______被直线______所截而成的____________.
a
b
a
b
c
同位角
c
d
c
d
b
同位角
1
2
A
B
C
D
例1.如图,∠1=∠C, ∠2=∠C,
请找出图中互相平行的直线,并说明理由.
典型例题
解:AB ∥ CD,AC ∥ BD
理由如下:
∵ ∠1=∠ C(已知)
∴ AB ∥ CD (同位角相等,两直线平行)
∵ ∠2=∠ C(已知)
∴ AC ∥ BD (同位角相等,两直线平行)
3
1
2
A
B
F
C
D
E
典型例题
例2.如图,∠1 = ∠2 = 55°,直线AB、CD平行吗? 说明你的理由.
解:AB ∥ CD
理由如下:
∵ ∠ 3和∠ 2是对顶角(已知)
∴ ∠ 3=∠ 2=55 ° (对顶角相等)
∵ ∠1=∠ 2=55 ° (已知)
∴ ∠ 3=∠ 1(等量代换)
∴ AB ∥ CD (同位角相等,两直线平行)
A
B
C
D
E
1
2
3
典型例题
例3.如图,∠A=500,∠BCE= 140°,AC⊥BD,直线AB、CE平行吗? 说明你的理由.
解:AB ∥ CE
理由如下:
∵ ∠ 3和∠ BCE是邻补角(已知)
∴ ∠ 3=180 ° - 140 ° =40 ° (邻补角互补)
∵ AC⊥BD (已知)
∴ ∠ 1=90 ° (垂直定义)
∴ ∠ B=180 ° - ∠ 1- ∠ A=40 °(三角形内角和为180 ° )
∴ ∠ B=∠ 3= 40 ° (等量代换)
∴ AB ∥ CE (同位角相等,两直线平行)
课堂小结
1. 同位角、内错角、同旁内角的概念.
2. 基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行。
3.识别两直线平行的方法:
同学们,再见!
7.1探索直线平行的条件(1)
1.会正确识别同位角、内错角、同旁内角.
2.探索基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
3.通过探索直线平行条件的过程,发展空间观念和有条理的表达能力.
学习目标
邻补角的概念:
对顶角的概念:
对顶角的性质:
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。
对顶角相等。
1
2
3
4
O
D
A
B
C
知识点回顾
∠1与∠3, ∠2与∠3,∠2与∠4,∠4与∠1
∠1与∠2, ∠3与∠4
∠1=∠2, ∠3=∠4
直线AB、CD与EF相交,构成八个角,如图所示,
问题一:八个角中有几对邻补角、有几对对顶角?
探索与思考
问题二:观察图中∠1和∠5,它们具有怎么的位置关系?
两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同侧(右侧).具有这种位置关系的一对角叫做同位角.
问题三:指出图中其他几组同位角?
∠2与∠6,∠3与∠7,∠4与∠8
图中∠1和∠5,在直线EF的__________,
在直线AB,CD的____________。
同侧(右侧)
同方向(上方)
如图∠1与∠2是同位角的个数有( )
A.1个 B.2个 C.3个 D.4个
【详解】
第一个图中∠1与∠2符合同位角的位置特征,是同位角;
第二个图中∠1与∠2符合同位角的位置特征,是同位角;
第三个图中∠1与∠2符合同位角的位置特征,是同位角;
第四个图中∠1与∠2符合同位角的位置特征,是同位角,
故选D.
巩固练习
直线AB、CD与EF相交,构成八个角,如图所示,
问题四:观察图中∠4和∠6,它们具有怎么的位置关系?
探索与思考
问题五:指出图中其他几组内错角?
两个角分别在直线AB、CD之间,并且分别在直线EF的两侧,具有这种位置关系的一对角叫做内错角.
∠3与∠5
图中∠4和∠6,
在直线EF的____________,
在直线AB,CD的____________。
两侧
内部
如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B.内错角 C.对顶角 D.同旁内角
【详解】
两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是内错角.故选B.
巩固练习
直线AB、CD与EF相交,构成八个角,如图所示,
问题六:观察图中∠3和∠6,它们具有怎么的位置关系?
探索与思考
问题七:指出图中其他的同旁内角?
两个角分别在直线AB、CD之间,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同旁内角.
∠4 与∠5
图中∠3和∠6,
在直线EF的____________,
在直线AB,CD的____________。
同侧(左侧)
内部
1.两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆,同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线,食指代表截线下列三幅图依次表示
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
巩固练习
2.如图,描述同位角、内错角、同旁内角关系不正确的是()
A.与∠4是同位角 B.与是内错角
C.与∠4是同旁内角 D.与∠4是同旁内角
【解析】
解:A.∠1与∠4是同位角,故A选项正确;
B.∠2与∠3是内错角,故B选项正确;
C.∠3与∠4是同旁内角,故C选项正确;
D.∠2与∠4是同旁内角,故D选项错误.
故选D.
巩固练习
3.如图,下列说法一定正确的是( )
A.∠1和∠4是内错角 B.∠1和∠3是同位角
C.∠3和∠4是同旁内角 D.∠1和∠C是同位角
【详解】
解:A、∠2和∠4是内错角,故本选项错误;
B、∠1和∠C是同位角,故本选项错误;
C、∠3和∠4是邻补角,故本选项错误;
D、∠1和∠C是同位角,故本选项正确;
故选:D.
巩固练面内两直线有何位置关系?
c
a
a
b
同一平面内,不相交的两条直线叫做平行线。
a
b
平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”。
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a。
平行线的概念:
表示方法:
知识点回顾
平行线的性质(平行公理):
·
P
a
b
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
a
b
c
几何语言表达式:
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:
∵ a∥b, b∥c (已知)
∴ a∥c (平行线的传递性)
知识点回顾
你能画出一条直线的平行线吗?
已知直线a,你能画出直线a的平行线吗?
a
b
平行线的画法 :一放、二靠、三推、四画。
观察∠1与∠2,你发现了什么?
P
a
b
c
1
2
A
B
P
画直线a的平行线b,实际就是过P点画与∠2相等的∠1,而∠1与∠2正是a,b被直线c截得同位角。
若同位角相等,则a∥b
探索新知
基本事实:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
几何语言:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
探索新知
你能说出木工用角尺画平行线的道理吗?
a
b
1
2
同位角相等,两直线平行
联系实际
如图,a、b、c、d是直线,E、F、G、H是交点,
(1)若∠1=∠2,可以证明______∥______,这是因为∠1和∠2是直线_______和_____被直线____所截而成的____________.
(2)若∠1=∠3,可以证明______∥______,这是因为∠1和∠3是直线______和______被直线______所截而成的____________.
a
b
a
b
c
同位角
c
d
c
d
b
同位角
1
2
A
B
C
D
例1.如图,∠1=∠C, ∠2=∠C,
请找出图中互相平行的直线,并说明理由.
典型例题
解:AB ∥ CD,AC ∥ BD
理由如下:
∵ ∠1=∠ C(已知)
∴ AB ∥ CD (同位角相等,两直线平行)
∵ ∠2=∠ C(已知)
∴ AC ∥ BD (同位角相等,两直线平行)
3
1
2
A
B
F
C
D
E
典型例题
例2.如图,∠1 = ∠2 = 55°,直线AB、CD平行吗? 说明你的理由.
解:AB ∥ CD
理由如下:
∵ ∠ 3和∠ 2是对顶角(已知)
∴ ∠ 3=∠ 2=55 ° (对顶角相等)
∵ ∠1=∠ 2=55 ° (已知)
∴ ∠ 3=∠ 1(等量代换)
∴ AB ∥ CD (同位角相等,两直线平行)
A
B
C
D
E
1
2
3
典型例题
例3.如图,∠A=500,∠BCE= 140°,AC⊥BD,直线AB、CE平行吗? 说明你的理由.
解:AB ∥ CE
理由如下:
∵ ∠ 3和∠ BCE是邻补角(已知)
∴ ∠ 3=180 ° - 140 ° =40 ° (邻补角互补)
∵ AC⊥BD (已知)
∴ ∠ 1=90 ° (垂直定义)
∴ ∠ B=180 ° - ∠ 1- ∠ A=40 °(三角形内角和为180 ° )
∴ ∠ B=∠ 3= 40 ° (等量代换)
∴ AB ∥ CE (同位角相等,两直线平行)
课堂小结
1. 同位角、内错角、同旁内角的概念.
2. 基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行。
3.识别两直线平行的方法:
同学们,再见!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
