苏科版数学七下7.2.1探索平行线的性质 课件(共15张PPT)
文档属性
| 名称 | 苏科版数学七下7.2.1探索平行线的性质 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 231.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
7.2探索平行线的性质(1)
( )
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
2
2
1
4
同位角相等,两直线平行
内错角相等,两直线平行
c
b
4
3
2
1
a
知识回顾
( )
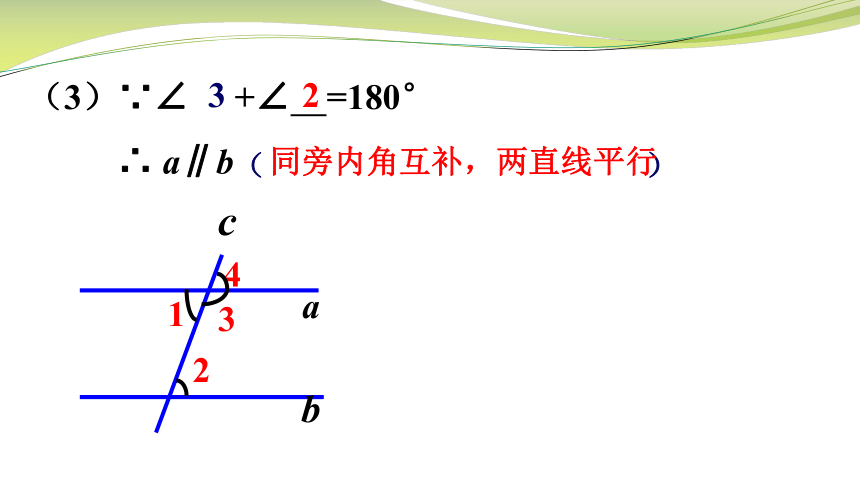
(3)∵∠ +∠ =180°
∴ a∥b
2
3
同旁内角互补,两直线平行
4
3
2
1
a
c
b
回顾小结
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
角的关系
线的关系
判定
如图,工人在修一条高速公路时前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向?
生活情境
数学实验
b
1
2
a
c
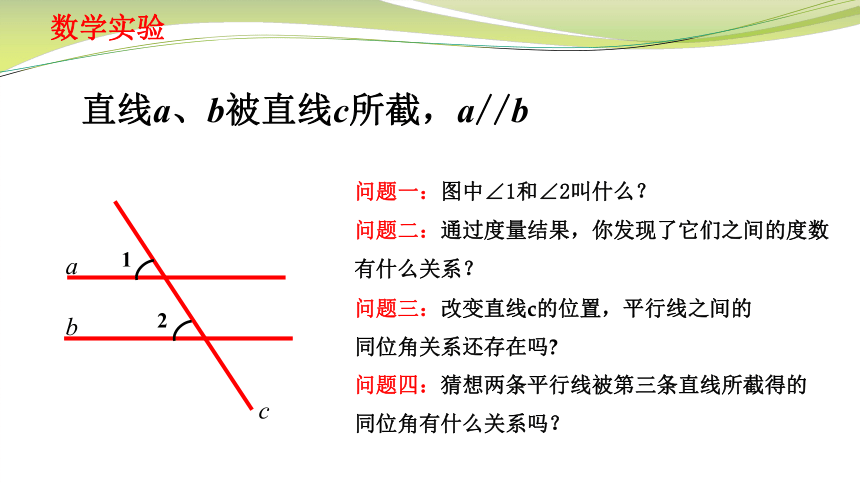
直线a、b被直线c所截,a//b
问题一:图中∠1和∠2叫什么?
问题二:通过度量结果,你发现了它们之间的度数
有什么关系?
问题三:改变直线c的位置,平行线之间的
同位角关系还存在吗
问题四:猜想两条平行线被第三条直线所截得的
同位角有什么关系吗?
平行线的性质1
文字语言:
两条平行线被第三条直线所截,同位角相等。
简写为:两直线平行,同位角相等。
几何语言:
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
概念梳理
概念巩固
【例1】 如图,已知直线a∥b,∠1 = 500, 求∠2的度数.
a
b
c
1
∴∠ 2= 500 (等量代换)
解:∵ a∥b(已知)
∴∠ 1= ∠ 2
(两直线平行,同位角相等)
又∵∠ 1 = 500 (已知)
2
【例2】如图, 已知AB∥EF,DE∥BC.那么图中∠ADE与∠EFC相等吗?为什么?
AB∥EF(已知)
∠ADE=∠B(两直线平行,同位角相等)
DE∥BC(已知)
∠B=∠EFC(两直线平行,同位角相等)
∠ADE=∠EFC(等量代换)
概念拓展
∴∠ 2= 470
( )
解:∵ ∠3 =∠4( )
∴a∥b
( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
两直线平行,同位角相等
同位角相等,两直线平行
已知
已知
已知∠3 =∠4,∠1=47°,求∠2的度数?
【例3】
概念拓展
线的关系
角的关系
判定
性质
课后小结
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
角的关系
线的关系
判定
两直线平行,同位角相等
如图,工人在修一条高速公路时前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向?
生活情境
【练习1】如图,已知CD∥BE, 如果∠1=80°, 那么∠B的度数为( )
A.70° B.100° C.110° D.125°
【答案】B
【详解】
解:∵∠1=80°,
∴∠2=180°- 80°=100°.
∵CD∥BE,
∴∠2=∠B=100°.
故选:B.
课后检测
【练习2】如图,B、C、D三点在一条直线上,∠A=75 ,∠1=55 ,∠2=75 ,求∠B的度数.
AB∥CE(内错角相等,两直线平行)
∠B=∠1=55 (两直线平行,同位角相等)
AB∥CE(已证)
∠A=∠2=75 (已知)
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
(1)求证DE∥BC(2) ∠C的度数
【练习3】
7.2探索平行线的性质(1)
( )
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
2
2
1
4
同位角相等,两直线平行
内错角相等,两直线平行
c
b
4
3
2
1
a
知识回顾
( )
(3)∵∠ +∠ =180°
∴ a∥b
2
3
同旁内角互补,两直线平行
4
3
2
1
a
c
b
回顾小结
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
角的关系
线的关系
判定
如图,工人在修一条高速公路时前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向?
生活情境
数学实验
b
1
2
a
c
直线a、b被直线c所截,a//b
问题一:图中∠1和∠2叫什么?
问题二:通过度量结果,你发现了它们之间的度数
有什么关系?
问题三:改变直线c的位置,平行线之间的
同位角关系还存在吗
问题四:猜想两条平行线被第三条直线所截得的
同位角有什么关系吗?
平行线的性质1
文字语言:
两条平行线被第三条直线所截,同位角相等。
简写为:两直线平行,同位角相等。
几何语言:
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
概念梳理
概念巩固
【例1】 如图,已知直线a∥b,∠1 = 500, 求∠2的度数.
a
b
c
1
∴∠ 2= 500 (等量代换)
解:∵ a∥b(已知)
∴∠ 1= ∠ 2
(两直线平行,同位角相等)
又∵∠ 1 = 500 (已知)
2
【例2】如图, 已知AB∥EF,DE∥BC.那么图中∠ADE与∠EFC相等吗?为什么?
AB∥EF(已知)
∠ADE=∠B(两直线平行,同位角相等)
DE∥BC(已知)
∠B=∠EFC(两直线平行,同位角相等)
∠ADE=∠EFC(等量代换)
概念拓展
∴∠ 2= 470
( )
解:∵ ∠3 =∠4( )
∴a∥b
( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
两直线平行,同位角相等
同位角相等,两直线平行
已知
已知
已知∠3 =∠4,∠1=47°,求∠2的度数?
【例3】
概念拓展
线的关系
角的关系
判定
性质
课后小结
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
角的关系
线的关系
判定
两直线平行,同位角相等
如图,工人在修一条高速公路时前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向?
生活情境
【练习1】如图,已知CD∥BE, 如果∠1=80°, 那么∠B的度数为( )
A.70° B.100° C.110° D.125°
【答案】B
【详解】
解:∵∠1=80°,
∴∠2=180°- 80°=100°.
∵CD∥BE,
∴∠2=∠B=100°.
故选:B.
课后检测
【练习2】如图,B、C、D三点在一条直线上,∠A=75 ,∠1=55 ,∠2=75 ,求∠B的度数.
AB∥CE(内错角相等,两直线平行)
∠B=∠1=55 (两直线平行,同位角相等)
AB∥CE(已证)
∠A=∠2=75 (已知)
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
(1)求证DE∥BC(2) ∠C的度数
【练习3】
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
