苏科版数学七下7.1.2探索直线平行的条件 课件(共22张PPT)
文档属性
| 名称 | 苏科版数学七下7.1.2探索直线平行的条件 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 11:51:09 | ||
图片预览






文档简介
(共22张PPT)
7.1探索直线平行的条件(2)
1.掌握平行线的识别方法,并初步运用它们进行简单的推理论证。
2.经历探索直线平行方法的探究过程,初步学会简单的论证和推理。
3. 初步了解转化的数学思想方法。
学习目标
A
B
C
D
E
1
3
2
4
5
6
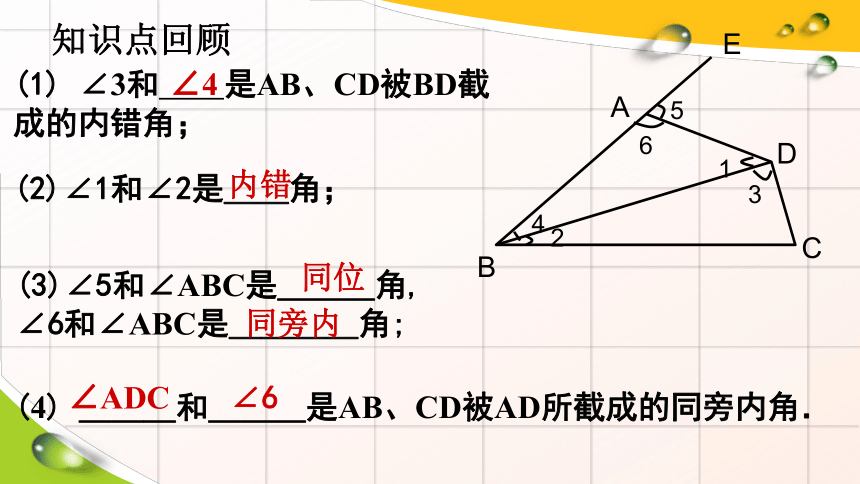
(1) ∠3和 是AB、CD被BD截成的内错角;
∠4
(2)∠1和∠2是__角;
(3)∠5和∠ABC是___角,
∠6和∠ABC是____角;
(4) ___和___是AB、CD被AD所截成的同旁内角.
内错
同位
同旁内
∠6
∠ADC
知识点回顾
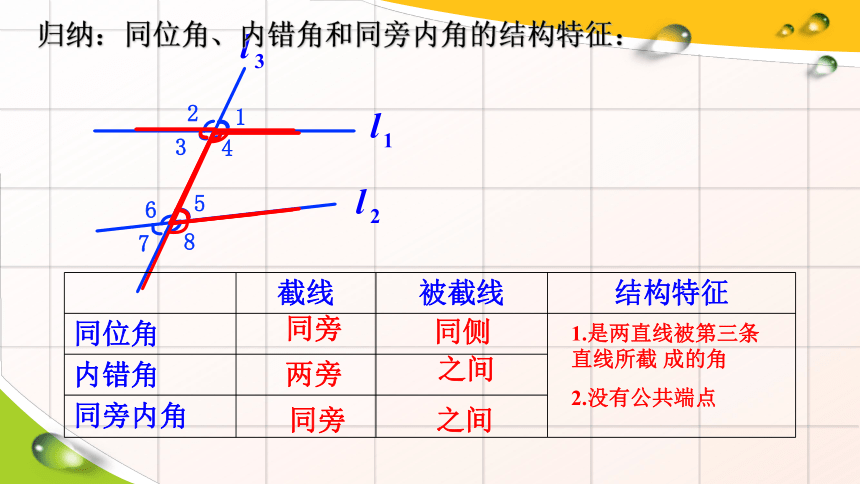
归纳:同位角、内错角和同旁内角的结构特征:
截线 被截线 结构特征
同位角
内错角 同旁内角 之间
之间
同侧
同旁
两旁
同旁
1.是两直线被第三条直线所截 成的角
2.没有公共端点
(5)找出图中互相平行的直线,并说明理由。
A
B
C
D
E
F
G
460
460
1340
知识点回顾
AB ∥ CD,BE ∥ DF
理由如下:
∵ ∠B=∠ CGE=46 °
∴ AB ∥ CD (同位角相等,两直线平行)
∵ ∠D=∠ CGE=46 °
∴ BE ∥ DF (同位角相等,两直线平行)
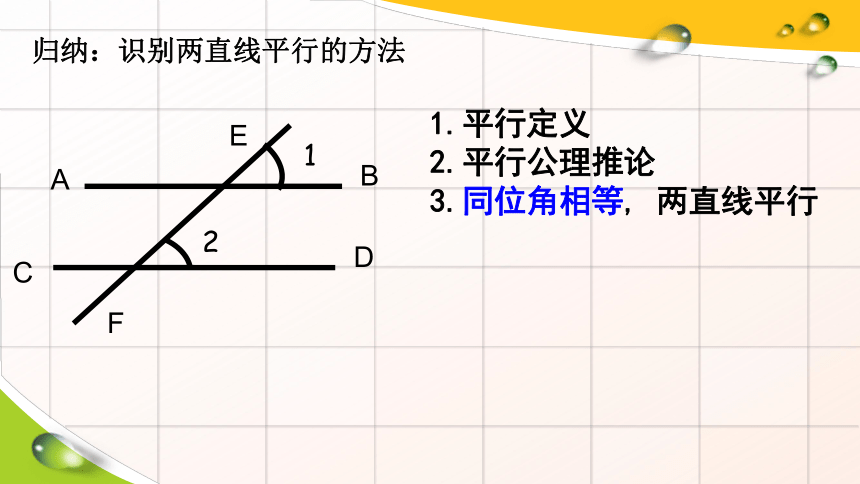
归纳:识别两直线平行的方法
1.平行定义
2.平行公理推论
3.同位角相等, 两直线平行
E
B
A
C
D
F
1
2
∵ ∠2=∠3(已知)
∠1=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a∥b(同位角相等,两直线平行)
证明思路
两直线平行
同位角相等
对顶角相等
内错角相等
两条直线被第三条直线所截,如果内错角相等,那么这两直线平行.简单说成:内错角相等,两直线平行
如图,已知∠2=∠3,试说明a∥b.
探索与思考
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
几何语言:
∵ ∠1=∠2(已知)
∴ a∥b(内错角相等,两直线平行)
平行线的识别方法
证明思路
两直线平行
同位角相等
两角互补
两角互补
两条直线被第三条直线所截,如果同旁内角互补,那么这两直线平行.简单说成:同旁内角互补,两直线平行.
探索与思考
∵ ∠2+∠3 =180° (已知)
∠1+∠3 =180°(邻补角互补)
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠2+∠3=180°,试说明a∥b.
两条直线被第三条直线所截,如果同旁同角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
几何语言:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
平行线的识别方法
归纳:识别两直线平行的方法
1.平行定义
2.平行公理推论
3.同位角相等, 两直线平行
E
B
A
C
D
F
1
2
4.内错角相等, 两直线平行
5.同旁内角互补, 两直线平行.
(5)找出图中互相平行的直线,并说明理由。
A
B
C
D
E
F
G
460
460
1340
知识点回顾
AB ∥ CD,BE ∥ DF
∵ ∠D+∠ DGE=180 °
∴ BE ∥ DF (同旁内角互补,两直线平行)
∵ ∠B+∠ BGC=180 °
∴ AB ∥ CD (同旁内角互补,两直线平行)
∵ ∠B=∠ BGD
∴ AB ∥ CD (内错角相等,两直线平行)
例1.如图,∠1=∠2,∠B+∠BDE=180°.指出图中互相平行的直线,并说明理由.
A
D
B
F
C
E
1
2
典型例题
解:AB ∥ EF,DE ∥ BC
理由如下:
∵ ∠1=∠ 2(已知)
∴ AB ∥ EF (内错角相等,两直线平行)
∵ ∠B+∠BDE=180°(已知)
∴ DE ∥ BC (同旁内角互补,两直线平行)
例2.如图∠A+∠B+∠C+∠D=360°,且∠A=∠C,
∠B=∠D,试说明AB∥CD,AD∥BC.
D
A
B
C
典型例题
解:∵ ∠A+∠B+∠C+∠D=360°(已知)
且∠A=∠C,∠B=∠D (已知)
∴ ∠A+∠B+∠A+∠B=360°(等量代换)
即 2∠A+2∠B=360°
∴ ∠A+∠B=180°
∴ AD ∥ BC (同旁内角互补,两直线平行)
同理 ∠A+∠D=180°
∴ AB ∥DC (同旁内角互补,两直线平行)
例3.如图,在四边形ABCD中,延长AD至E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.
(1)说明AB∥CD;
(2)求∠2的度数.
解:(1)∵AC平分∠DAB, ∠DAB=70°(已知)
∴ ∠ DAC = ∠ CAB =35 ° (角平分线定义)
∵ ∠1=35°(已知)
∴ ∠1= ∠ CAB =35 ° (等量代换)
∴ AB ∥ CD (内错角相等,两直线平行)
典型例题
(2) ∵∠2是△ADC的外角
∴ ∠2 = ∠ DAC +∠1=70°(三角形的一个外角等于和它不相邻的两个内角和)
1.如图,一个弯形管道ABCD的拐角∠ABC=110°,
∠BCD=70°,这时管道AB、CD平行吗
联系实际
2.如图,三个相同的三角尺拼接成一个图形,请找出图中的一组平行线,并说明你的理由.
联系实际
1.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠5 D.∠3+∠4=180°
【详解】
解:A.∵∠1与∠2是直线a,b被c所截的一组同位角,∴∠1=∠2,可以得到a∥b,∴不符合题意
B.∵∠2与∠3是直线a,b被c所截的一组内错角,∴∠2=∠3,可以得到a∥b,∴不符合题意,
C.∵∠3与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,∴∠3=∠5,不能得到a∥b,∴符合题意,
D.∵∠3与∠4是直线a,b被c所截的一组同旁内角,∴∠3+∠4=180°,可以得到a∥b,∴不符合题意,故选C.
巩固练习
2.如图所示,点E在AB的延长线上,下列条件中不能判断AB//CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠C=∠CBE D.∠C+∠ABC=180°
【详解】
A、 ∠1和∠2是内错角,根据内错角相等,两直线平行,可得AB∥CD,故此选项不合题意;
B、 ∠3和∠4是内错角,根据内错角相等,两直线平行,可得AD∥BC,故此选项符合题意;
C、 ∠C和∠CBE是内错角,根据内错角相等,两直线平行,可得AB∥CD,故此选项不合题意;
D、 ∠C和∠ABC是同旁内角,根据同旁内角互补,两直线平行,可得AB∥CD,故此选项不合题意;故选B.
巩固练习
如图,下列条件:中能判断直线l1与l2的有( )
A.5个 B.4个 C.3个 D.2个
【详解】
解:①∵∠1=∠3,∴l1∥l2,故本小题正确;
②∵∠2+∠4=180°,∴l1∥l2,故本小题正确;
③∵∠4=∠5,∴l1∥l2,故本小题正确;
④∠2=∠3不能判定l1∥l2,故本小题错误;
⑤∵∠6=∠2+∠3且∠6=∠2+∠1,故∠1=∠3 ∴l1∥l2,故本小题正确.
故选:B.
巩固练习
掌握识别直线平行的
方法
01
直线平行的识别方法的探究、逻辑推理及书面表达
02
初步了解转换的数学思想
03
课堂小结
E
B
A
C
D
F
同学们,再见!
7.1探索直线平行的条件(2)
1.掌握平行线的识别方法,并初步运用它们进行简单的推理论证。
2.经历探索直线平行方法的探究过程,初步学会简单的论证和推理。
3. 初步了解转化的数学思想方法。
学习目标
A
B
C
D
E
1
3
2
4
5
6
(1) ∠3和 是AB、CD被BD截成的内错角;
∠4
(2)∠1和∠2是__角;
(3)∠5和∠ABC是___角,
∠6和∠ABC是____角;
(4) ___和___是AB、CD被AD所截成的同旁内角.
内错
同位
同旁内
∠6
∠ADC
知识点回顾
归纳:同位角、内错角和同旁内角的结构特征:
截线 被截线 结构特征
同位角
内错角 同旁内角 之间
之间
同侧
同旁
两旁
同旁
1.是两直线被第三条直线所截 成的角
2.没有公共端点
(5)找出图中互相平行的直线,并说明理由。
A
B
C
D
E
F
G
460
460
1340
知识点回顾
AB ∥ CD,BE ∥ DF
理由如下:
∵ ∠B=∠ CGE=46 °
∴ AB ∥ CD (同位角相等,两直线平行)
∵ ∠D=∠ CGE=46 °
∴ BE ∥ DF (同位角相等,两直线平行)
归纳:识别两直线平行的方法
1.平行定义
2.平行公理推论
3.同位角相等, 两直线平行
E
B
A
C
D
F
1
2
∵ ∠2=∠3(已知)
∠1=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a∥b(同位角相等,两直线平行)
证明思路
两直线平行
同位角相等
对顶角相等
内错角相等
两条直线被第三条直线所截,如果内错角相等,那么这两直线平行.简单说成:内错角相等,两直线平行
如图,已知∠2=∠3,试说明a∥b.
探索与思考
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
几何语言:
∵ ∠1=∠2(已知)
∴ a∥b(内错角相等,两直线平行)
平行线的识别方法
证明思路
两直线平行
同位角相等
两角互补
两角互补
两条直线被第三条直线所截,如果同旁内角互补,那么这两直线平行.简单说成:同旁内角互补,两直线平行.
探索与思考
∵ ∠2+∠3 =180° (已知)
∠1+∠3 =180°(邻补角互补)
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠2+∠3=180°,试说明a∥b.
两条直线被第三条直线所截,如果同旁同角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
几何语言:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
平行线的识别方法
归纳:识别两直线平行的方法
1.平行定义
2.平行公理推论
3.同位角相等, 两直线平行
E
B
A
C
D
F
1
2
4.内错角相等, 两直线平行
5.同旁内角互补, 两直线平行.
(5)找出图中互相平行的直线,并说明理由。
A
B
C
D
E
F
G
460
460
1340
知识点回顾
AB ∥ CD,BE ∥ DF
∵ ∠D+∠ DGE=180 °
∴ BE ∥ DF (同旁内角互补,两直线平行)
∵ ∠B+∠ BGC=180 °
∴ AB ∥ CD (同旁内角互补,两直线平行)
∵ ∠B=∠ BGD
∴ AB ∥ CD (内错角相等,两直线平行)
例1.如图,∠1=∠2,∠B+∠BDE=180°.指出图中互相平行的直线,并说明理由.
A
D
B
F
C
E
1
2
典型例题
解:AB ∥ EF,DE ∥ BC
理由如下:
∵ ∠1=∠ 2(已知)
∴ AB ∥ EF (内错角相等,两直线平行)
∵ ∠B+∠BDE=180°(已知)
∴ DE ∥ BC (同旁内角互补,两直线平行)
例2.如图∠A+∠B+∠C+∠D=360°,且∠A=∠C,
∠B=∠D,试说明AB∥CD,AD∥BC.
D
A
B
C
典型例题
解:∵ ∠A+∠B+∠C+∠D=360°(已知)
且∠A=∠C,∠B=∠D (已知)
∴ ∠A+∠B+∠A+∠B=360°(等量代换)
即 2∠A+2∠B=360°
∴ ∠A+∠B=180°
∴ AD ∥ BC (同旁内角互补,两直线平行)
同理 ∠A+∠D=180°
∴ AB ∥DC (同旁内角互补,两直线平行)
例3.如图,在四边形ABCD中,延长AD至E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.
(1)说明AB∥CD;
(2)求∠2的度数.
解:(1)∵AC平分∠DAB, ∠DAB=70°(已知)
∴ ∠ DAC = ∠ CAB =35 ° (角平分线定义)
∵ ∠1=35°(已知)
∴ ∠1= ∠ CAB =35 ° (等量代换)
∴ AB ∥ CD (内错角相等,两直线平行)
典型例题
(2) ∵∠2是△ADC的外角
∴ ∠2 = ∠ DAC +∠1=70°(三角形的一个外角等于和它不相邻的两个内角和)
1.如图,一个弯形管道ABCD的拐角∠ABC=110°,
∠BCD=70°,这时管道AB、CD平行吗
联系实际
2.如图,三个相同的三角尺拼接成一个图形,请找出图中的一组平行线,并说明你的理由.
联系实际
1.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠5 D.∠3+∠4=180°
【详解】
解:A.∵∠1与∠2是直线a,b被c所截的一组同位角,∴∠1=∠2,可以得到a∥b,∴不符合题意
B.∵∠2与∠3是直线a,b被c所截的一组内错角,∴∠2=∠3,可以得到a∥b,∴不符合题意,
C.∵∠3与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,∴∠3=∠5,不能得到a∥b,∴符合题意,
D.∵∠3与∠4是直线a,b被c所截的一组同旁内角,∴∠3+∠4=180°,可以得到a∥b,∴不符合题意,故选C.
巩固练习
2.如图所示,点E在AB的延长线上,下列条件中不能判断AB//CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠C=∠CBE D.∠C+∠ABC=180°
【详解】
A、 ∠1和∠2是内错角,根据内错角相等,两直线平行,可得AB∥CD,故此选项不合题意;
B、 ∠3和∠4是内错角,根据内错角相等,两直线平行,可得AD∥BC,故此选项符合题意;
C、 ∠C和∠CBE是内错角,根据内错角相等,两直线平行,可得AB∥CD,故此选项不合题意;
D、 ∠C和∠ABC是同旁内角,根据同旁内角互补,两直线平行,可得AB∥CD,故此选项不合题意;故选B.
巩固练习
如图,下列条件:中能判断直线l1与l2的有( )
A.5个 B.4个 C.3个 D.2个
【详解】
解:①∵∠1=∠3,∴l1∥l2,故本小题正确;
②∵∠2+∠4=180°,∴l1∥l2,故本小题正确;
③∵∠4=∠5,∴l1∥l2,故本小题正确;
④∠2=∠3不能判定l1∥l2,故本小题错误;
⑤∵∠6=∠2+∠3且∠6=∠2+∠1,故∠1=∠3 ∴l1∥l2,故本小题正确.
故选:B.
巩固练习
掌握识别直线平行的
方法
01
直线平行的识别方法的探究、逻辑推理及书面表达
02
初步了解转换的数学思想
03
课堂小结
E
B
A
C
D
F
同学们,再见!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
