苏科版数学七下7.5.3多边形的内角和与外角和 课件(共17张PPT)
文档属性
| 名称 | 苏科版数学七下7.5.3多边形的内角和与外角和 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 466.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
初 一 数 学
7.5 多边形的内角和与外角和(3)
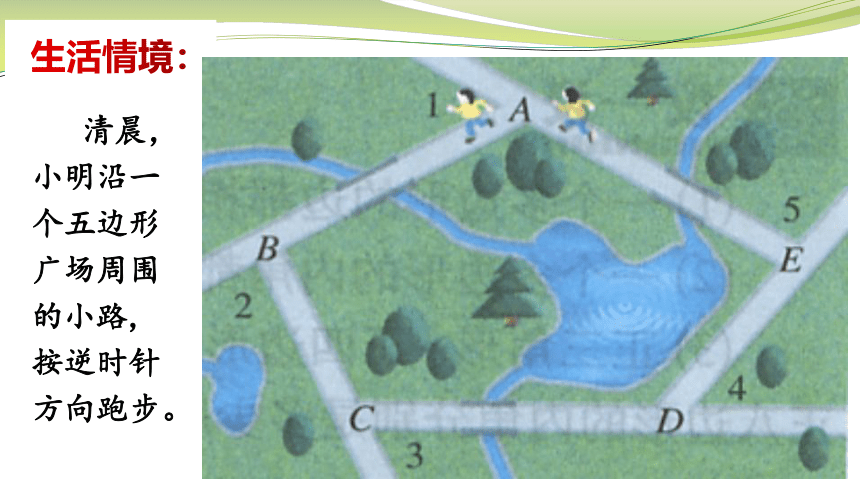
生活情境:
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
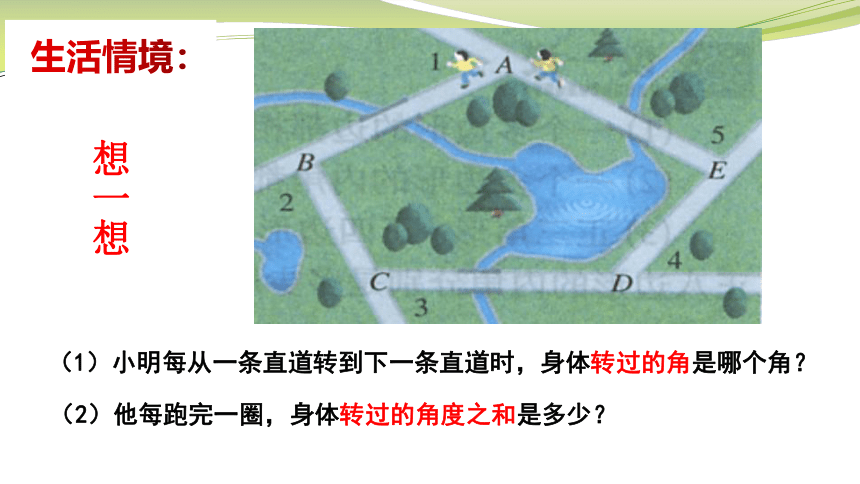
(1)小明每从一条直道转到下一条直道时,身体转过的角是哪个角?
想一想
(2)他每跑完一圈,身体转过的角度之和是多少?
生活情境:
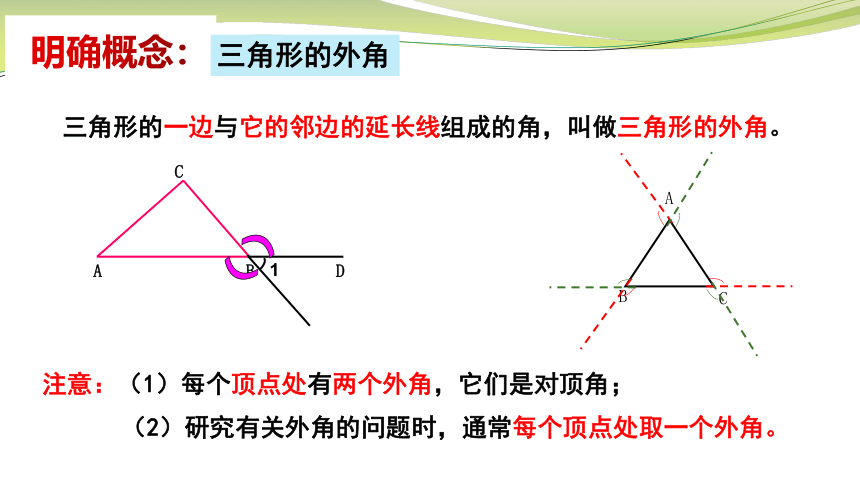
明确概念:
三角形的外角
三角形的一边与它的邻边的延长线组成的角,叫做三角形的外角。
A
B
C
注意:(1)每个顶点处有两个外角,它们是对顶角;
(2)研究有关外角的问题时,通常每个顶点处取一个外角。
A
B
C
D
1
明确概念:
外角
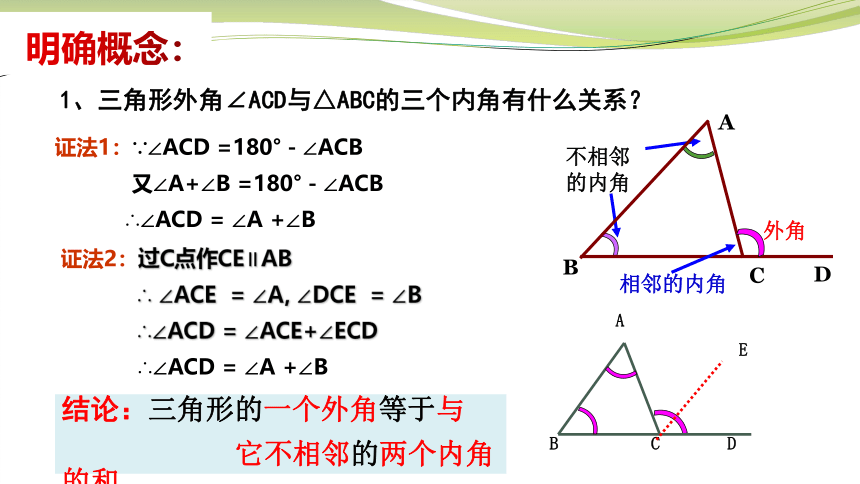
1、三角形外角∠ACD与△ABC的三个内角有什么关系?
相邻的内角
不相邻的内角
A
C
B
D
结论:三角形的一个外角等于与
它不相邻的两个内角的和
B
D
A
C
E
证法1:∵∠ACD =180°-∠ACB
又∠A+∠B =180°-∠ACB
∴∠ACD = ∠A +∠B
证法2:过C点作CE∥AB
∴ ∠ACE = ∠A, ∠DCE = ∠B
∴∠ACD = ∠ACE+∠ECD
∴∠ACD = ∠A +∠B
A
C
B
D
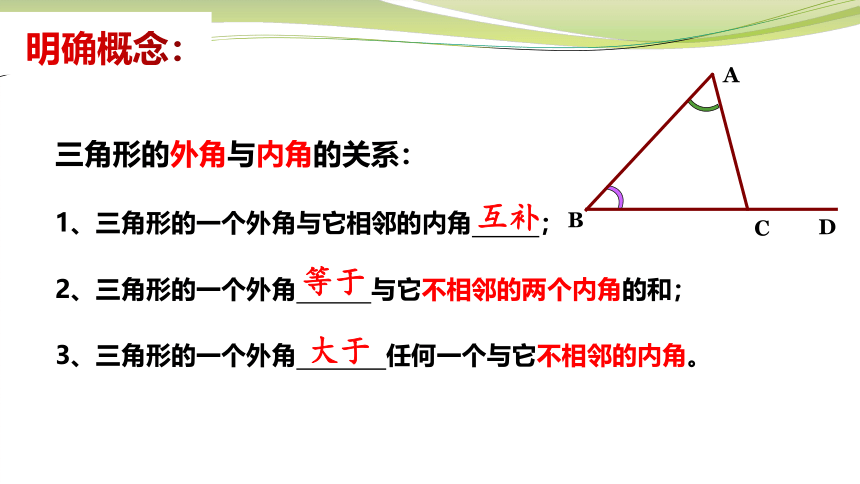
三角形的外角与内角的关系:
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的两个内角的和;
3、三角形的一个外角 任何一个与它不相邻的内角。
等于
大于
互补
明确概念:
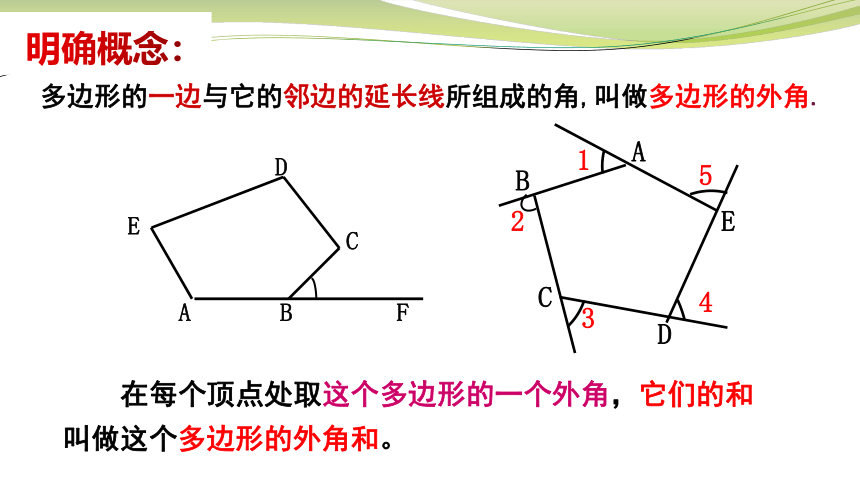
多边形的一边与它的邻边的延长线所组成的角,叫做多边形的外角.
A
B
C
D
E
在每个顶点处取这个多边形的一个外角,它们的和
叫做这个多边形的外角和。
A
B
C
D
E
1
2
3
4
5
F
明确概念:
探究活动:
1.(1)任意画一个△ABC,在△ABC每个顶点处取这个三角形的一
个外角,分别为∠α、∠β、∠γ.
你发现了什么
(2)把3个外角剪下来,然后将它们的顶点A、B、C重合在同一
点O,拼成右图.
∠α+∠β+∠γ = 360°
A
B
C
1
2
3
β
γ
α
α
β
γ
探究活动:
A
B
C
1
2
3
β
γ
α
(3)聪明的你是否还有其它方法得到:
∠α+∠β+∠γ = 360°
∠α+ ∠1=180°,
∠β+ ∠2=180°,
∠γ +∠3=180°,
∠1+∠2+∠3= 180°
则∠α+∠β+∠γ =
360°
三角形的外角和等于360°
探究活动:
2.四边形的外角和等于多少度
(1)仿照上面的试一试.
(2)∠α+∠1=180°,
∠β+∠2=180°,
∠γ+∠3=180°,
∠δ+∠4=180°,
∠1+∠2+∠3+ ∠4 = 180°×2
则∠α+∠β+∠γ+∠δ = .
360°
A
B
C
1
2
3
β
γ
α
D
δ
4
四边形的外角和等于360°
探究活动:
3.你能求出五边形的外角和吗
A
B
C
D
E
1
2
3
4
5
五边形的外角和也等于360°.
180°×5-(5-2)×180°
= 360°.
探究活动:
4.猜想:n边形的外角和等于多少度
因为多边形的外角与它相邻的内角是邻补角,
所以n边形的外角和加内角和等于n·180°,
而内角和为(n-2)·180°,
则外角和为:n·180°-(n-2)·180°= 360°.
结论:任意多边形的外角和都等于360°.
多边形的外角和与边数无关
尝试练习:
1.一个多边形的每一个外角都是60°,这个多边形是几边形 它的内角和等于多少度
2.若一个多边形的外角和与它的内角和相等,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
解:设多边形的边数为n.
根据题意得:(n-2)×180°=360°,解得:n=4.
B
解:设边数为n.n×60°=360°,n=6.
拓展:一个多边形的内角和比外角和的倍多,则它的边数是( )
A.七 B.八 C.九 D.十
解:设边数为n,则(n-2) 180°=3×360°+180°,得n=9,
则这个多边形的边数是9.
C
尝试练习:
3.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米 B.150米
C.160米 D.240米
解:已知多边形的外角和为360°,而每一个外角为24°,可得多边形的边数为360°÷24°=15,所以小明一共走了:15×10=150米.
尝试练习:
B
360°
学习有方法,解题有技巧.
初 一 数 学
7.5 多边形的内角和与外角和(3)
生活情境:
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)小明每从一条直道转到下一条直道时,身体转过的角是哪个角?
想一想
(2)他每跑完一圈,身体转过的角度之和是多少?
生活情境:
明确概念:
三角形的外角
三角形的一边与它的邻边的延长线组成的角,叫做三角形的外角。
A
B
C
注意:(1)每个顶点处有两个外角,它们是对顶角;
(2)研究有关外角的问题时,通常每个顶点处取一个外角。
A
B
C
D
1
明确概念:
外角
1、三角形外角∠ACD与△ABC的三个内角有什么关系?
相邻的内角
不相邻的内角
A
C
B
D
结论:三角形的一个外角等于与
它不相邻的两个内角的和
B
D
A
C
E
证法1:∵∠ACD =180°-∠ACB
又∠A+∠B =180°-∠ACB
∴∠ACD = ∠A +∠B
证法2:过C点作CE∥AB
∴ ∠ACE = ∠A, ∠DCE = ∠B
∴∠ACD = ∠ACE+∠ECD
∴∠ACD = ∠A +∠B
A
C
B
D
三角形的外角与内角的关系:
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的两个内角的和;
3、三角形的一个外角 任何一个与它不相邻的内角。
等于
大于
互补
明确概念:
多边形的一边与它的邻边的延长线所组成的角,叫做多边形的外角.
A
B
C
D
E
在每个顶点处取这个多边形的一个外角,它们的和
叫做这个多边形的外角和。
A
B
C
D
E
1
2
3
4
5
F
明确概念:
探究活动:
1.(1)任意画一个△ABC,在△ABC每个顶点处取这个三角形的一
个外角,分别为∠α、∠β、∠γ.
你发现了什么
(2)把3个外角剪下来,然后将它们的顶点A、B、C重合在同一
点O,拼成右图.
∠α+∠β+∠γ = 360°
A
B
C
1
2
3
β
γ
α
α
β
γ
探究活动:
A
B
C
1
2
3
β
γ
α
(3)聪明的你是否还有其它方法得到:
∠α+∠β+∠γ = 360°
∠α+ ∠1=180°,
∠β+ ∠2=180°,
∠γ +∠3=180°,
∠1+∠2+∠3= 180°
则∠α+∠β+∠γ =
360°
三角形的外角和等于360°
探究活动:
2.四边形的外角和等于多少度
(1)仿照上面的试一试.
(2)∠α+∠1=180°,
∠β+∠2=180°,
∠γ+∠3=180°,
∠δ+∠4=180°,
∠1+∠2+∠3+ ∠4 = 180°×2
则∠α+∠β+∠γ+∠δ = .
360°
A
B
C
1
2
3
β
γ
α
D
δ
4
四边形的外角和等于360°
探究活动:
3.你能求出五边形的外角和吗
A
B
C
D
E
1
2
3
4
5
五边形的外角和也等于360°.
180°×5-(5-2)×180°
= 360°.
探究活动:
4.猜想:n边形的外角和等于多少度
因为多边形的外角与它相邻的内角是邻补角,
所以n边形的外角和加内角和等于n·180°,
而内角和为(n-2)·180°,
则外角和为:n·180°-(n-2)·180°= 360°.
结论:任意多边形的外角和都等于360°.
多边形的外角和与边数无关
尝试练习:
1.一个多边形的每一个外角都是60°,这个多边形是几边形 它的内角和等于多少度
2.若一个多边形的外角和与它的内角和相等,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
解:设多边形的边数为n.
根据题意得:(n-2)×180°=360°,解得:n=4.
B
解:设边数为n.n×60°=360°,n=6.
拓展:一个多边形的内角和比外角和的倍多,则它的边数是( )
A.七 B.八 C.九 D.十
解:设边数为n,则(n-2) 180°=3×360°+180°,得n=9,
则这个多边形的边数是9.
C
尝试练习:
3.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米 B.150米
C.160米 D.240米
解:已知多边形的外角和为360°,而每一个外角为24°,可得多边形的边数为360°÷24°=15,所以小明一共走了:15×10=150米.
尝试练习:
B
360°
学习有方法,解题有技巧.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
