苏科版数学七下7.5.2多边形的内角和与外角和 课件(共23张PPT)
文档属性
| 名称 | 苏科版数学七下7.5.2多边形的内角和与外角和 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
初 一 数 学
7.5 多边形的内角和与外角和(2)
温故知新:
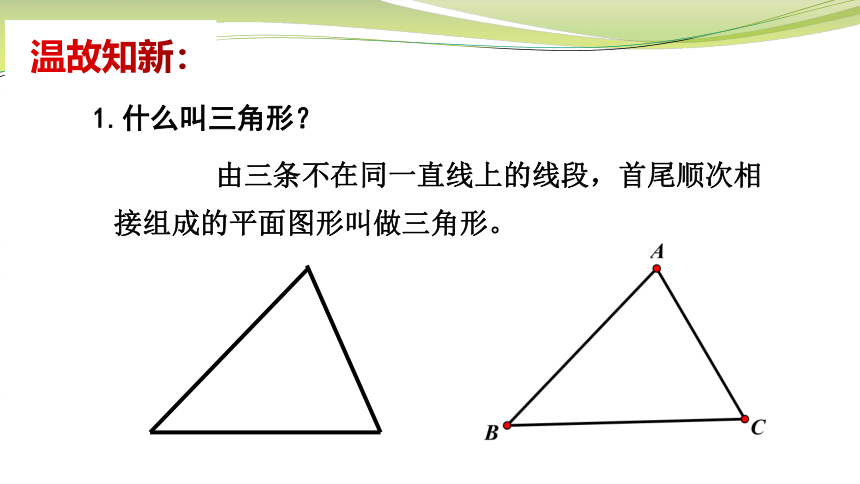
1.什么叫三角形?
由三条不在同一直线上的线段,首尾顺次相接组成的平面图形叫做三角形。
明确概念:
2.多边形的概念
在同一平面内,由不在同一条直线上的三条或三条以上线段首尾依次相接组成的图形叫做多边形。
……
五边形
六边形
七边形
三角形
四边形
三角形是边数最少的多边形
A2
A4
A5
An
A3
A1
顶点
内角
边
n边形
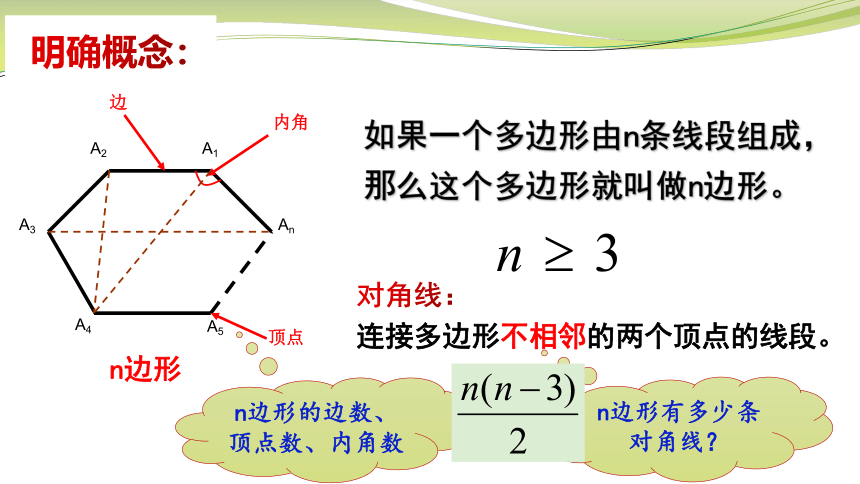
对角线:
连接多边形不相邻的两个顶点的线段。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
明确概念:
n边形的边数、顶点数、内角数
n边形有多少条对角线?
明确概念:
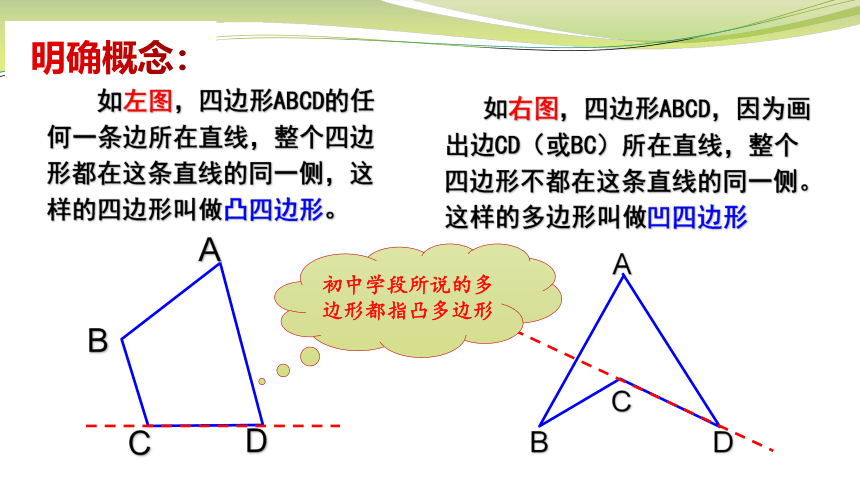
如左图,四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形。
A
B
C
D
如右图,四边形ABCD,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧。这样的多边形叫做凹四边形
A
B
D
C
初中学段所说的多边形都指凸多边形
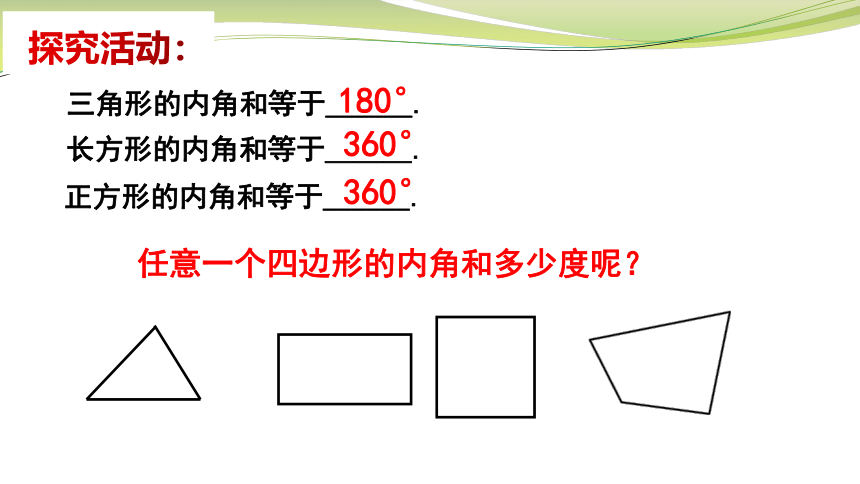
三角形的内角和等于______.
180°
任意一个四边形的内角和多少度呢?
长方形的内角和等于______.
正方形的内角和等于______.
360°
360°
探究活动:
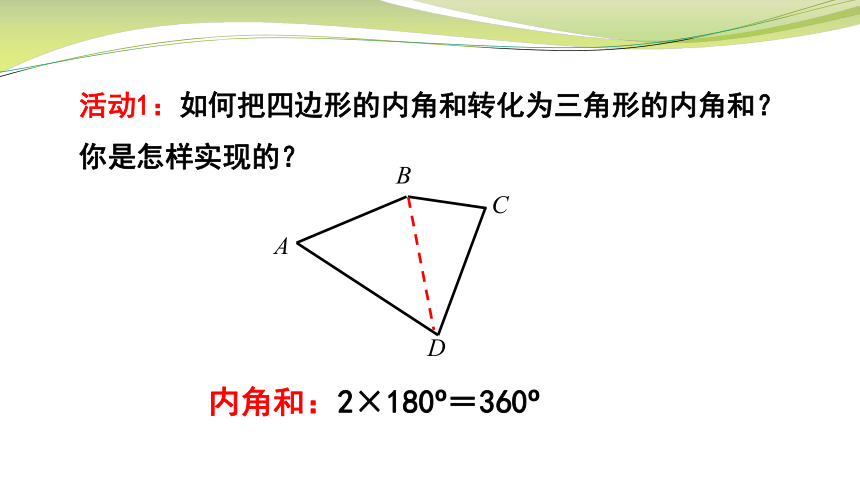
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
D
C
B
A
探究活动:
D
C
B
A
内角和:2×180 =360
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?
A
C
D
B
内角和:3×180°-180°=360°
.
E
⌒
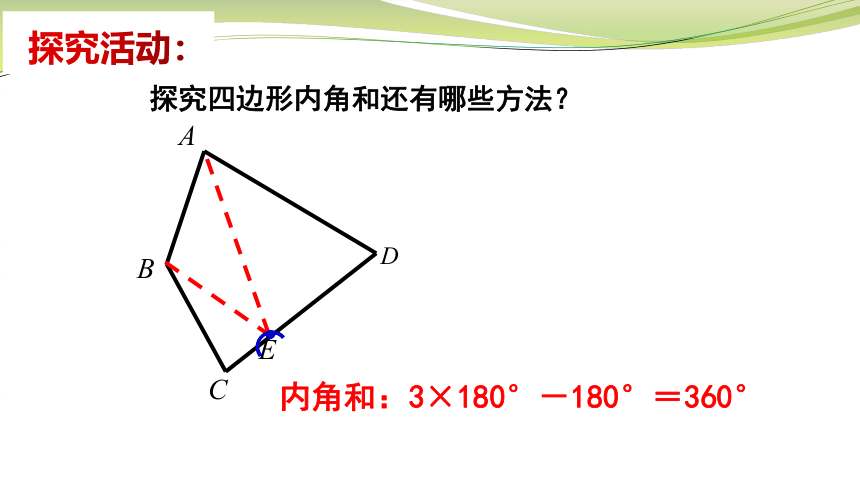
探究四边形内角和还有哪些方法?
探究活动:
内角和:4×180°-360 °=360 °
D
C
B
A
E
.
探究四边形内角和还有哪些方法?
探究活动:
A
C
D
B
E
内角和:3×180 -180 =360
.
探究四边形内角和还有哪些方法?
探究活动:
A
C
D
B
C
A
D
B
.
O
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
D
C
B
A
E
.
探究活动:
活动2.选择其中一种方法探索四边形的内角和.
从四边形的一个顶点出发,可以作_____条对角线,它们将
四边形分为 个三角形,四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
探究活动:
A
B
C
D
E
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180 × = .
2
3
3
540
活动2.选择其中一种方法探索五边形的内角和.
探究活动:
如图,从六边形的一个顶点出发,可以作_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于
180°×___=_____°.
3
4
4
720
C
A
B
D
E
F
活动2.选择其中一种方法探索六边形的内角和.
探究活动:
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
活动2.你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
探究活动:
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
······
······
0
3-3 =
4-3 =
5-3 =
6-3 =
n-3
1
2
3
3-2 =
1
4-2 =
2
5-2 =
3
6-2 =
4
n-2
( n-2 )·180
1×180
2×180
3×180
4×180
······
······
······
归纳总结
探究活动:
探究活动:
n边形的内角和等于(n-2)×180°
多边形的内角和:
多边形的内角和随着边数n的变化而变化
例题赏析:
例题.如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F.∠1与∠2有怎样的数量关系?为什么?
1
2
解:
由四边形ABCD的内角和360°,以及
∠A与∠C互补,可得∠ADC+∠ABC=180°.
又知BE、DF分别是∠ABC、∠ADC的平分线
所以∠1与∠2互余.
变形.如图,在四边形ABCD中,∠A=∠C=90°,∠ABC、∠ADC的平分线分别交CD、AB于点E、F.BE和DF有怎样的位置关系?为什么?
例题赏析:
□
□
1
2
3
证∠1=∠3,得BE∥DF
尝试练习:
2.一个多边形的内角和等于1440°,它是几边形?
1.求图中x的值.
3.已知四边形ABCD中,∠A∶∠B∶∠C∶∠D =3:4:5:6,分别求出最大角和最小角的度数.
解:依题意可设∠A=3x°,∠B=4x°, ∠C=5x°,∠D=6x °,由题意得:
3x+4x+5x+6x=(4-2)×180
18x=2×180
x=20
答:最大角和最小角分别为120°,60°.
6x=120, 3x=60
学习有方法,解题有技巧.
初 一 数 学
7.5 多边形的内角和与外角和(2)
温故知新:
1.什么叫三角形?
由三条不在同一直线上的线段,首尾顺次相接组成的平面图形叫做三角形。
明确概念:
2.多边形的概念
在同一平面内,由不在同一条直线上的三条或三条以上线段首尾依次相接组成的图形叫做多边形。
……
五边形
六边形
七边形
三角形
四边形
三角形是边数最少的多边形
A2
A4
A5
An
A3
A1
顶点
内角
边
n边形
对角线:
连接多边形不相邻的两个顶点的线段。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
明确概念:
n边形的边数、顶点数、内角数
n边形有多少条对角线?
明确概念:
如左图,四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形。
A
B
C
D
如右图,四边形ABCD,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧。这样的多边形叫做凹四边形
A
B
D
C
初中学段所说的多边形都指凸多边形
三角形的内角和等于______.
180°
任意一个四边形的内角和多少度呢?
长方形的内角和等于______.
正方形的内角和等于______.
360°
360°
探究活动:
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
D
C
B
A
探究活动:
D
C
B
A
内角和:2×180 =360
活动1:如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?
A
C
D
B
内角和:3×180°-180°=360°
.
E
⌒
探究四边形内角和还有哪些方法?
探究活动:
内角和:4×180°-360 °=360 °
D
C
B
A
E
.
探究四边形内角和还有哪些方法?
探究活动:
A
C
D
B
E
内角和:3×180 -180 =360
.
探究四边形内角和还有哪些方法?
探究活动:
A
C
D
B
C
A
D
B
.
O
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
D
C
B
A
E
.
探究活动:
活动2.选择其中一种方法探索四边形的内角和.
从四边形的一个顶点出发,可以作_____条对角线,它们将
四边形分为 个三角形,四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
探究活动:
A
B
C
D
E
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180 × = .
2
3
3
540
活动2.选择其中一种方法探索五边形的内角和.
探究活动:
如图,从六边形的一个顶点出发,可以作_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于
180°×___=_____°.
3
4
4
720
C
A
B
D
E
F
活动2.选择其中一种方法探索六边形的内角和.
探究活动:
从n 边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.
活动2.你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?
探究活动:
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
······
······
0
3-3 =
4-3 =
5-3 =
6-3 =
n-3
1
2
3
3-2 =
1
4-2 =
2
5-2 =
3
6-2 =
4
n-2
( n-2 )·180
1×180
2×180
3×180
4×180
······
······
······
归纳总结
探究活动:
探究活动:
n边形的内角和等于(n-2)×180°
多边形的内角和:
多边形的内角和随着边数n的变化而变化
例题赏析:
例题.如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F.∠1与∠2有怎样的数量关系?为什么?
1
2
解:
由四边形ABCD的内角和360°,以及
∠A与∠C互补,可得∠ADC+∠ABC=180°.
又知BE、DF分别是∠ABC、∠ADC的平分线
所以∠1与∠2互余.
变形.如图,在四边形ABCD中,∠A=∠C=90°,∠ABC、∠ADC的平分线分别交CD、AB于点E、F.BE和DF有怎样的位置关系?为什么?
例题赏析:
□
□
1
2
3
证∠1=∠3,得BE∥DF
尝试练习:
2.一个多边形的内角和等于1440°,它是几边形?
1.求图中x的值.
3.已知四边形ABCD中,∠A∶∠B∶∠C∶∠D =3:4:5:6,分别求出最大角和最小角的度数.
解:依题意可设∠A=3x°,∠B=4x°, ∠C=5x°,∠D=6x °,由题意得:
3x+4x+5x+6x=(4-2)×180
18x=2×180
x=20
答:最大角和最小角分别为120°,60°.
6x=120, 3x=60
学习有方法,解题有技巧.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
