2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试卷(Word版含答案) | 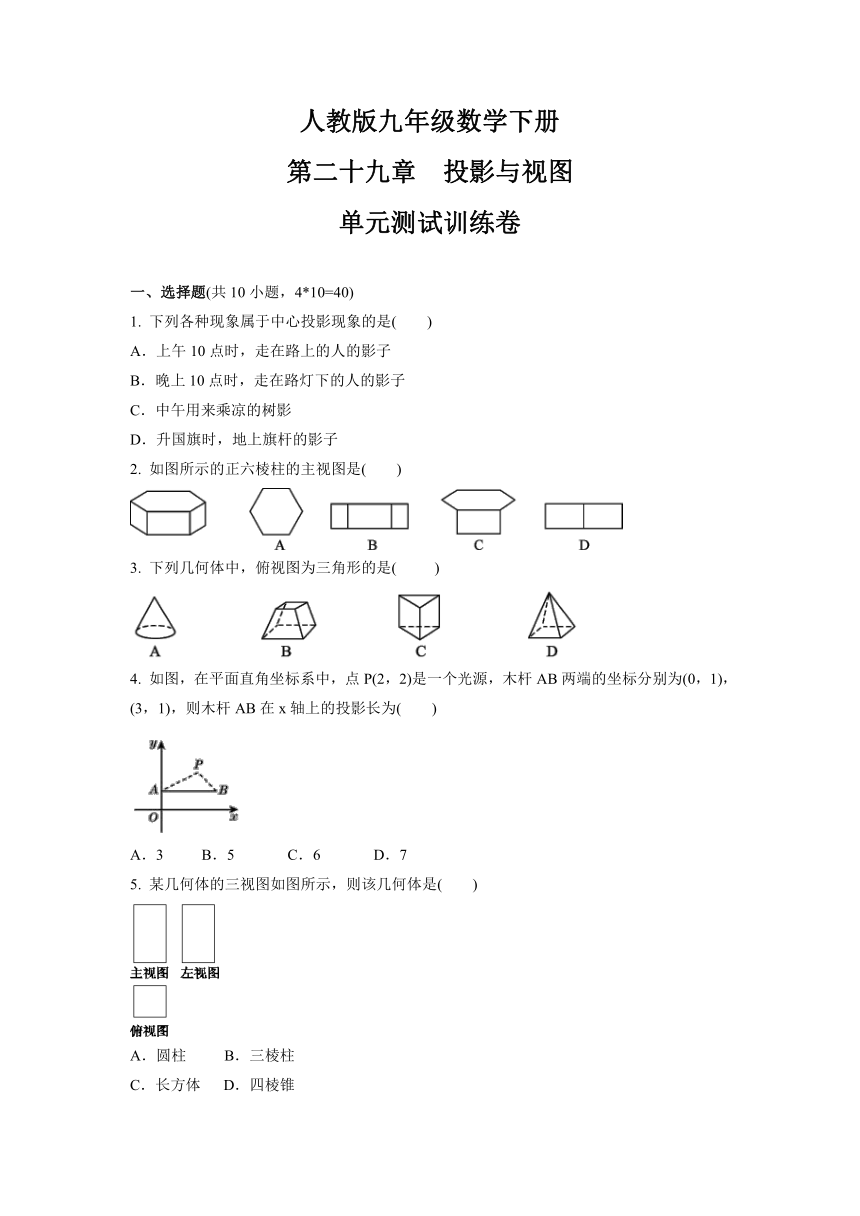 | |
| 格式 | docx | ||
| 文件大小 | 445.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 12:17:38 | ||
图片预览


文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列各种现象属于中心投影现象的是( )
A.上午10点时,走在路上的人的影子
B.晚上10点时,走在路灯下的人的影子
C.中午用来乘凉的树影
D.升国旗时,地上旗杆的影子
2. 如图所示的正六棱柱的主视图是( )
3. 下列几何体中,俯视图为三角形的是( )
4. 如图,在平面直角坐标系中,点P(2,2)是一个光源,木杆AB两端的坐标分别为(0,1),(3,1),则木杆AB在x轴上的投影长为( )
A.3 B.5 C.6 D.7
5. 某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.三棱柱
C.长方体 D.四棱锥
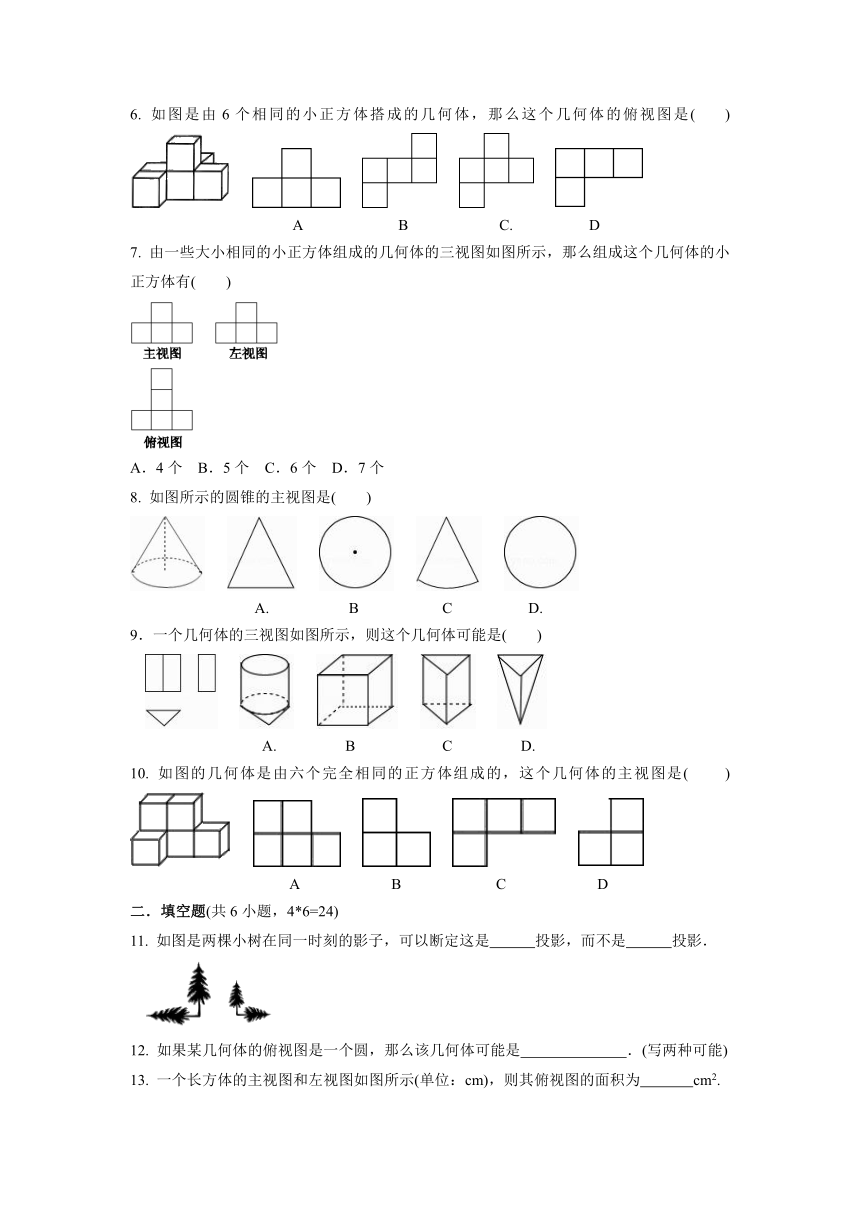
6. 如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
A B C. D
7. 由一些大小相同的小正方体组成的几何体的三视图如图所示,那么组成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
8. 如图所示的圆锥的主视图是( )
A. B C D.
9.一个几何体的三视图如图所示,则这个几何体可能是( )
A. B C D.
10. 如图的几何体是由六个完全相同的正方体组成的,这个几何体的主视图是( )
A B C D
二.填空题(共6小题,4*6=24)
11. 如图是两棵小树在同一时刻的影子,可以断定这是 投影,而不是 投影.
12. 如果某几何体的俯视图是一个圆,那么该几何体可能是 .(写两种可能)
13. 一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积为 cm2.
14. 对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时,物体的投影;④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.其中正确的是________(把所有正确说法的序号都填上).
15.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,问:结果会________ (“溢出”、“刚好”、“未装满”,选一个)
16.在桌面上摆放着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为________.
三.解答题(共5小题, 56分)
17.(6分) 画出下面几何体的三视图.
18.(8分) 如图是某种几何体的三视图,
(1)这个几何体是什么;
(2)若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2?(结果用π表示).
19.(8分) 观察:下图中的几何体是由若干个完全相同的小正方体搭成的.
(1)画出几何体的主视图,左视图,俯视图;
(2)能移走一个小正方体使它的三个视图都不变吗?
20.(10分) 某几何体的俯视图是一个圆,如图是这个几何体的展开图,请求出它的表面积,并画出这个几何体的三视图.
21.(12分) 圆锥的底面周长为6π cm,高为4 cm,求该圆锥的表面积与侧面展开图(扇形)的圆心角的度数.
22.(12分) 由大小相同的小正方体搭成的几何体如图1所示,根据几何体,回答下列问题.
(1)请在图2的方格中画出该几何体的俯视图和左视图;
(2)用小正方体搭一个几何体,使得它的俯视图和左视图与(1)所画的一致,则这样的几何体最少要________个小正方体,最多要________个小正方体;
(3)将此几何体露在外面的部分涂上油漆(不包含底面),其中两面涂色的小正方体有________块.
参考答案
1-5BBCCC 6-10CCACA
11.中心,平行
12.答案不唯一,如:圆柱或球体
13.6
14.①
15. 未装满
16. 5
17.解:如图所示:
18. 解:(1)根据图形得到这个几何体为:圆柱,故答案为:圆柱;
(2)表面积为:2(25π)+10π×20=250π(m2)
19. 解:(1)如图所示
(2)如图,去掉粉打了☆号的立方体,三视图不变
20. 由展开图想象出几何体的形状是上部分为圆锥、下部分为圆柱的组合体,且圆锥的底面积与圆柱的底面积相等,所以表面积S=×8π×5+8π×20+π×42=196π.三视图如图所示:
21. 解:设圆锥的底面半径为r cm,母线长为R cm,侧面展开图(扇形)的圆心角为n°.∵圆锥的底面周长为2πr=6π,∴r=3.∵圆锥的高为4 cm,∴R==5,∴圆锥的表面积=底面积+侧面积=π×32+×6π×5=24π(cm2).∵侧面展开图(扇形)的弧长l=底面周长=6π=,∴n==216,即侧面展开扇形的圆心角是216°.答:该圆锥的表面积为24π cm2,侧面展开图(扇形)的圆心角的度数为216°.
22. 解:(1)如图所示:
(2)由俯视图易得最底层有6个小正方体,由左视图知第二层最少有2个小正方体,第三层最少有1个小正方体,所以最少有6+2+1=9(个)小正方体.最底层有6个小正方体,第二层最多有5个小正方体,第三层最多有3个小正方体,所以最多有6+5+3=14(个)小正方体.故答案为:9 14.
(3)将此几何体露在外面的部分涂上油漆(不包含底面),其中两面涂色的小正方体有2块.故答案为:2.
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列各种现象属于中心投影现象的是( )
A.上午10点时,走在路上的人的影子
B.晚上10点时,走在路灯下的人的影子
C.中午用来乘凉的树影
D.升国旗时,地上旗杆的影子
2. 如图所示的正六棱柱的主视图是( )
3. 下列几何体中,俯视图为三角形的是( )
4. 如图,在平面直角坐标系中,点P(2,2)是一个光源,木杆AB两端的坐标分别为(0,1),(3,1),则木杆AB在x轴上的投影长为( )
A.3 B.5 C.6 D.7
5. 某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.三棱柱
C.长方体 D.四棱锥
6. 如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
A B C. D
7. 由一些大小相同的小正方体组成的几何体的三视图如图所示,那么组成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
8. 如图所示的圆锥的主视图是( )
A. B C D.
9.一个几何体的三视图如图所示,则这个几何体可能是( )
A. B C D.
10. 如图的几何体是由六个完全相同的正方体组成的,这个几何体的主视图是( )
A B C D
二.填空题(共6小题,4*6=24)
11. 如图是两棵小树在同一时刻的影子,可以断定这是 投影,而不是 投影.
12. 如果某几何体的俯视图是一个圆,那么该几何体可能是 .(写两种可能)
13. 一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积为 cm2.
14. 对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时,物体的投影;④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.其中正确的是________(把所有正确说法的序号都填上).
15.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,问:结果会________ (“溢出”、“刚好”、“未装满”,选一个)
16.在桌面上摆放着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为________.
三.解答题(共5小题, 56分)
17.(6分) 画出下面几何体的三视图.
18.(8分) 如图是某种几何体的三视图,
(1)这个几何体是什么;
(2)若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2?(结果用π表示).
19.(8分) 观察:下图中的几何体是由若干个完全相同的小正方体搭成的.
(1)画出几何体的主视图,左视图,俯视图;
(2)能移走一个小正方体使它的三个视图都不变吗?
20.(10分) 某几何体的俯视图是一个圆,如图是这个几何体的展开图,请求出它的表面积,并画出这个几何体的三视图.
21.(12分) 圆锥的底面周长为6π cm,高为4 cm,求该圆锥的表面积与侧面展开图(扇形)的圆心角的度数.
22.(12分) 由大小相同的小正方体搭成的几何体如图1所示,根据几何体,回答下列问题.
(1)请在图2的方格中画出该几何体的俯视图和左视图;
(2)用小正方体搭一个几何体,使得它的俯视图和左视图与(1)所画的一致,则这样的几何体最少要________个小正方体,最多要________个小正方体;
(3)将此几何体露在外面的部分涂上油漆(不包含底面),其中两面涂色的小正方体有________块.
参考答案
1-5BBCCC 6-10CCACA
11.中心,平行
12.答案不唯一,如:圆柱或球体
13.6
14.①
15. 未装满
16. 5
17.解:如图所示:
18. 解:(1)根据图形得到这个几何体为:圆柱,故答案为:圆柱;
(2)表面积为:2(25π)+10π×20=250π(m2)
19. 解:(1)如图所示
(2)如图,去掉粉打了☆号的立方体,三视图不变
20. 由展开图想象出几何体的形状是上部分为圆锥、下部分为圆柱的组合体,且圆锥的底面积与圆柱的底面积相等,所以表面积S=×8π×5+8π×20+π×42=196π.三视图如图所示:
21. 解:设圆锥的底面半径为r cm,母线长为R cm,侧面展开图(扇形)的圆心角为n°.∵圆锥的底面周长为2πr=6π,∴r=3.∵圆锥的高为4 cm,∴R==5,∴圆锥的表面积=底面积+侧面积=π×32+×6π×5=24π(cm2).∵侧面展开图(扇形)的弧长l=底面周长=6π=,∴n==216,即侧面展开扇形的圆心角是216°.答:该圆锥的表面积为24π cm2,侧面展开图(扇形)的圆心角的度数为216°.
22. 解:(1)如图所示:
(2)由俯视图易得最底层有6个小正方体,由左视图知第二层最少有2个小正方体,第三层最少有1个小正方体,所以最少有6+2+1=9(个)小正方体.最底层有6个小正方体,第二层最多有5个小正方体,第三层最多有3个小正方体,所以最多有6+5+3=14(个)小正方体.故答案为:9 14.
(3)将此几何体露在外面的部分涂上油漆(不包含底面),其中两面涂色的小正方体有2块.故答案为:2.
