2021-2022学年北师大版九年级数学下册第三章圆单元复习卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第三章圆单元复习卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 354.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 12:18:05 | ||
图片预览


文档简介
北师大版九年级数学下册
第三章 圆
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 如图,刚升的太阳和地平线的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
2. 如图,将△ABC绕着点A顺时针旋转30°得到△AB'C',若∠BAC'=80°,则∠B'AC等于( )
A.20° B.25° C.30° D.35°
3. 如图,把边长为12的等边三角形纸板剪去三个全等的小等边三角形,得到一个正六边形,则这个正六边形的边长是( )
A.6 B.4 C.8 D.9
4. 如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上的一点,DC是⊙O的切线,C是切点,连结AC,BC,若∠BCD=∠CAB=30°,则BD的长为( )
A.2R B.R C.R D.R
5. 如图,在⊙O中,AB是直径,BC是弦,点P是上任意一点,连接AP.若AB=5,BC=3,则AP的长不可能为( )
A.3 B.4 C. D.5
6. 如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
7. △ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.100° D.80°或100°
8. 如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( )
A.69° B.42° C.48° D.38°
9.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8㎝,则AC的长是( )
A. 6cm B. 8cm C. cm D. cm
10. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F.P是⊙A上一点,且∠EPF=40°,则图中阴影部分的面积是( )
A.4- B.4- C.8- D.8-
二.填空题(共6小题,4*6=24)
11. 如图,已知AD为⊙O的切线,⊙O的直径AB=2,弦AC=1,∠CAD=________°.
12. 如图,在⊙O中,已知∠A CB=∠CDB=60○ ,AC=3,则△ABC的周长是 ;
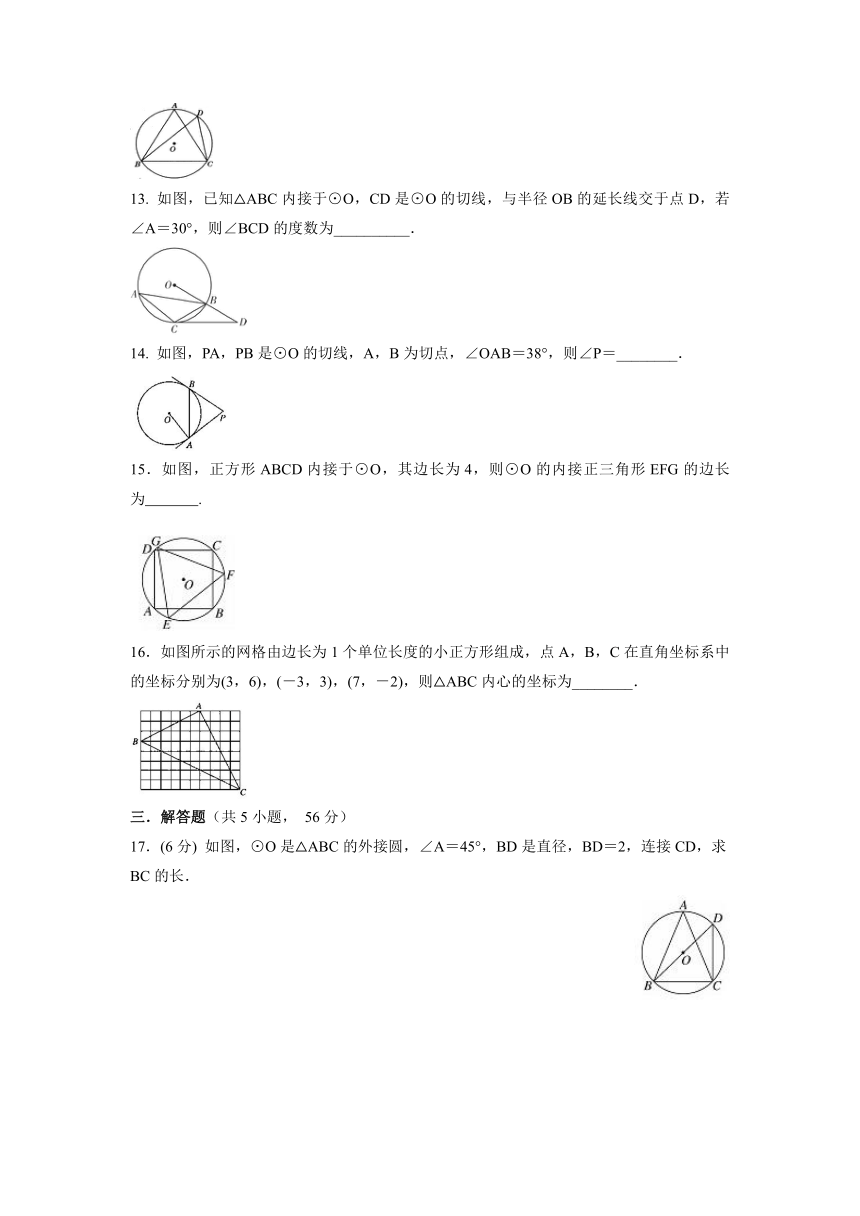
13. 如图,已知△ABC内接于⊙O,CD是⊙O的切线,与半径OB的延长线交于点D,若∠A=30°,则∠BCD的度数为__________.
14. 如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=________.
15.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
16.如图所示的网格由边长为1个单位长度的小正方形组成,点A,B,C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为________.
三.解答题(共5小题, 56分)
17.(6分) 如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
18.(8分) 如图,点C在⊙O上,连接CO并延长交弦AB于点D,=,连接AC,OB,若CD=8,AC=4.求弦AB的长及sin∠ABO的值.
19.(8分) 如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
20.(10分) 如图,△ABC内接于⊙O,OD⊥BC于点D,∠OCD=40°,求弦BC所对圆周角的度数.
21.(12分) 如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求的长.(结果保留π)
22.(12分) 如图,AB是☉O的直径,C是的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,☉O的半径为5,求BC的长.
参考答案
1-5BABCA 6-10ADADB
11.30 12. 9 13.30° 14.76° 15.2 16.(2,3)
17. 解:在⊙O中,∵∠A=45°,∴∠D=45°.∵BD为⊙O的直径,∴∠BCD=90°,∴BC=BD·sin45°=2×=.
18. 解:∵CD过圆心O,=,∴CD⊥AB,AB=2AD=2BD,∵CD=8,AC=4,∠ADC=90°,∴AD==4,∴AB=2AD=8;设圆O的半径为r,则OD=8-r,∵BD=AD=4,∠ODB=90°,∴BD2+OD2=OB2,即42+(8-r)2=r2,解得r=5,OD=3,∴sin∠ABO==
19. 解:(1)∵AD∥BC,∠ADC=120°,∴∠BCD=60°,∠DAC=∠ACB.又∵CA平分∠BCD,∴∠DCA=∠ACB=∠DAC=30°.∴==,∠B=60°.∴∠BAC=90°,∴BC是圆的直径,BC=2AB.∵四边形ABCD的周长为10,∴AB=AD=DC=2,BC=4.∴此圆的半径为2.
(2)设BC的中点为O.由(1)可知点O即为圆心,如图所示.连接OA,OD,过点O作OE⊥AD于点E,在Rt△AOE中,易知∠AOE=30°,∴OE=OA·cos 30°=.∴S阴影=S扇形AOD-S△AOD=-×2× =-.
20.解:连接OB,∵OD⊥BC于D,∠OCD=40°,∴∠DOC=50°,又OB=OC,∴∠OBD=40°,可求得∠BOD=50°,∴∠BOC=100°,∴∠BAC=∠BOC=50°,在劣弧上找点E,连接BE,CE,则∠BEC+∠BAC=180°,∴∠BEC=130°,即弦BC所对的圆周角的度数为50°或130°
21.(1)证明:∵AD平分∠BAC,∴∠CAD=∠BAD.∵∠CAD=∠CBD,∴∠BAD=∠CBD.
(2)如图,连接OD.∵∠AEB=125°,∴∠AEC=55°.∵AB为⊙O的直径,∴∠ACE=90°.∴∠CAE=35°.∴∠DAB=∠CAE=35°.∵OA=OD,∴∠DAB=∠ADO=35°.∴∠BOD=2∠BAD=70°.∵AB=6,∴OB=3.∴的长为 =.
22.解:(1)证明:连结AC,如图①所示.∵C是的中点,∴=,∴∠DBC=∠BAC.∵AB是☉O的直径,∴∠ACB=90°,∴∠BCE+∠ECA=90°.又∵CE⊥AB,∴∠BAC+∠ECA=90°,∴∠BCE=∠BAC,∴∠BCE=∠DBC,∴CF=BF.
(2)连结OC交BD于点G,如图②所示.∵AB是☉O的直径,∴AB=2OC=10,∠ADB=90°,∴BD===8.∵C是的中点,∴OC⊥BD,DG=BG=BD=4.∵OA=OB,∴OG是△ABD的中位线,∴OG=AD=3,∴CG=OC-OG=5-3=2.在Rt△BCG中,由勾股定理得BC===2.
第三章 圆
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 如图,刚升的太阳和地平线的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
2. 如图,将△ABC绕着点A顺时针旋转30°得到△AB'C',若∠BAC'=80°,则∠B'AC等于( )
A.20° B.25° C.30° D.35°
3. 如图,把边长为12的等边三角形纸板剪去三个全等的小等边三角形,得到一个正六边形,则这个正六边形的边长是( )
A.6 B.4 C.8 D.9
4. 如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上的一点,DC是⊙O的切线,C是切点,连结AC,BC,若∠BCD=∠CAB=30°,则BD的长为( )
A.2R B.R C.R D.R
5. 如图,在⊙O中,AB是直径,BC是弦,点P是上任意一点,连接AP.若AB=5,BC=3,则AP的长不可能为( )
A.3 B.4 C. D.5
6. 如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
7. △ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.100° D.80°或100°
8. 如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( )
A.69° B.42° C.48° D.38°
9.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8㎝,则AC的长是( )
A. 6cm B. 8cm C. cm D. cm
10. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F.P是⊙A上一点,且∠EPF=40°,则图中阴影部分的面积是( )
A.4- B.4- C.8- D.8-
二.填空题(共6小题,4*6=24)
11. 如图,已知AD为⊙O的切线,⊙O的直径AB=2,弦AC=1,∠CAD=________°.
12. 如图,在⊙O中,已知∠A CB=∠CDB=60○ ,AC=3,则△ABC的周长是 ;
13. 如图,已知△ABC内接于⊙O,CD是⊙O的切线,与半径OB的延长线交于点D,若∠A=30°,则∠BCD的度数为__________.
14. 如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=________.
15.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
16.如图所示的网格由边长为1个单位长度的小正方形组成,点A,B,C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为________.
三.解答题(共5小题, 56分)
17.(6分) 如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
18.(8分) 如图,点C在⊙O上,连接CO并延长交弦AB于点D,=,连接AC,OB,若CD=8,AC=4.求弦AB的长及sin∠ABO的值.
19.(8分) 如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
20.(10分) 如图,△ABC内接于⊙O,OD⊥BC于点D,∠OCD=40°,求弦BC所对圆周角的度数.
21.(12分) 如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求的长.(结果保留π)
22.(12分) 如图,AB是☉O的直径,C是的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,☉O的半径为5,求BC的长.
参考答案
1-5BABCA 6-10ADADB
11.30 12. 9 13.30° 14.76° 15.2 16.(2,3)
17. 解:在⊙O中,∵∠A=45°,∴∠D=45°.∵BD为⊙O的直径,∴∠BCD=90°,∴BC=BD·sin45°=2×=.
18. 解:∵CD过圆心O,=,∴CD⊥AB,AB=2AD=2BD,∵CD=8,AC=4,∠ADC=90°,∴AD==4,∴AB=2AD=8;设圆O的半径为r,则OD=8-r,∵BD=AD=4,∠ODB=90°,∴BD2+OD2=OB2,即42+(8-r)2=r2,解得r=5,OD=3,∴sin∠ABO==
19. 解:(1)∵AD∥BC,∠ADC=120°,∴∠BCD=60°,∠DAC=∠ACB.又∵CA平分∠BCD,∴∠DCA=∠ACB=∠DAC=30°.∴==,∠B=60°.∴∠BAC=90°,∴BC是圆的直径,BC=2AB.∵四边形ABCD的周长为10,∴AB=AD=DC=2,BC=4.∴此圆的半径为2.
(2)设BC的中点为O.由(1)可知点O即为圆心,如图所示.连接OA,OD,过点O作OE⊥AD于点E,在Rt△AOE中,易知∠AOE=30°,∴OE=OA·cos 30°=.∴S阴影=S扇形AOD-S△AOD=-×2× =-.
20.解:连接OB,∵OD⊥BC于D,∠OCD=40°,∴∠DOC=50°,又OB=OC,∴∠OBD=40°,可求得∠BOD=50°,∴∠BOC=100°,∴∠BAC=∠BOC=50°,在劣弧上找点E,连接BE,CE,则∠BEC+∠BAC=180°,∴∠BEC=130°,即弦BC所对的圆周角的度数为50°或130°
21.(1)证明:∵AD平分∠BAC,∴∠CAD=∠BAD.∵∠CAD=∠CBD,∴∠BAD=∠CBD.
(2)如图,连接OD.∵∠AEB=125°,∴∠AEC=55°.∵AB为⊙O的直径,∴∠ACE=90°.∴∠CAE=35°.∴∠DAB=∠CAE=35°.∵OA=OD,∴∠DAB=∠ADO=35°.∴∠BOD=2∠BAD=70°.∵AB=6,∴OB=3.∴的长为 =.
22.解:(1)证明:连结AC,如图①所示.∵C是的中点,∴=,∴∠DBC=∠BAC.∵AB是☉O的直径,∴∠ACB=90°,∴∠BCE+∠ECA=90°.又∵CE⊥AB,∴∠BAC+∠ECA=90°,∴∠BCE=∠BAC,∴∠BCE=∠DBC,∴CF=BF.
(2)连结OC交BD于点G,如图②所示.∵AB是☉O的直径,∴AB=2OC=10,∠ADB=90°,∴BD===8.∵C是的中点,∴OC⊥BD,DG=BG=BD=4.∵OA=OB,∴OG是△ABD的中位线,∴OG=AD=3,∴CG=OC-OG=5-3=2.在Rt△BCG中,由勾股定理得BC===2.
