2021—2022学年人教版数学七年级下册5.1相交线限时作业(基础)(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版数学七年级下册5.1相交线限时作业(基础)(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 12:23:17 | ||
图片预览

文档简介
2021~2022人教版数学七年级下册
第1周限时作业(基础)(5.1相交线)(含答案)
一、单选题(共6题;共18分)
1.(3分)(2018七下·钦州期末)如图,已知∠1=120°,则∠2的度数是( )
A.120° B.90° C.60° D.30°
2.(3分)(2020七上·扬州期末)点P为直线外一点,点A、B在直线l上,若PA=4cm,PB=5cm,则点P到直线l的距离是( )
A.4cm B.小于4cm C.不大于4cm D.5cm
3.(3分)(2021七下·娄星期末)如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是( )
A.6 B.8 C.10 D.4.8
4.(3分)(2021七下·涵江期末)如图,点A、C、B在同一直线上,DC⊥EC,若∠BCD=40°,则∠ACE的度数是( )
A.30° B.40° C.50° D.60°
5.(3分)(2020七下·余杭期末)如图,射线AB,AC被射线DE所截,图中的∠1与∠2是( )
A.内错角 B.对顶角 C.同位角 D.同旁内角
6.(3分)(2021七下·凤山月考)如图,在线段PA,PB,PC,PD中,长度最小的是( )
A.线段PA B.线段 PC C.线段PB D.线段PD
二、填空题(共6题;共28分)
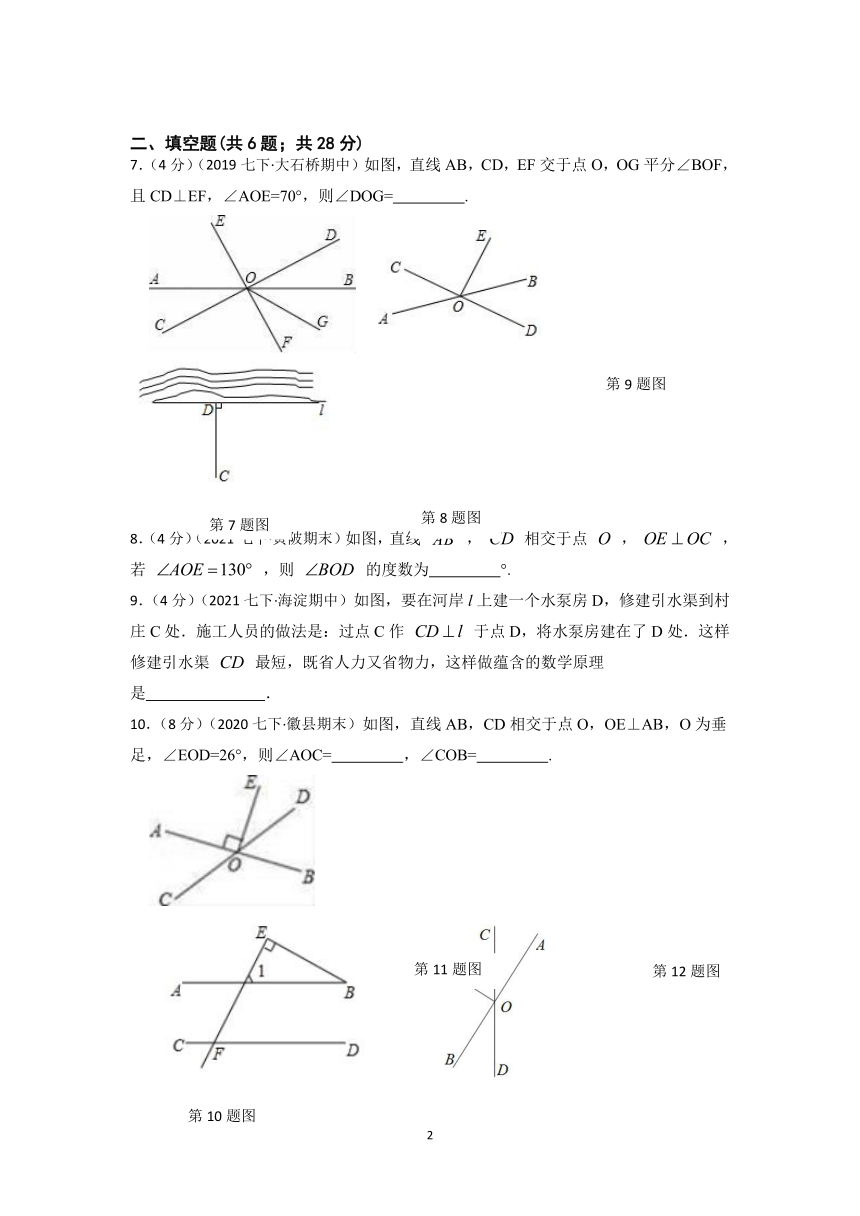
7.(4分)(2019七下·大石桥期中)如图,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,则∠DOG= .
8.(4分)(2021七下·黄陂期末)如图,直线 , 相交于点 , ,若 ,则 的度数为 °.
9.(4分)(2021七下·海淀期中)如图,要在河岸l上建一个水泵房D,修建引水渠到村庄C处.施工人员的做法是:过点C作 于点D,将水泵房建在了D处.这样修建引水渠 最短,既省人力又省物力,这样做蕴含的数学原理是 .
10.(8分)(2020七下·徽县期末)如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC= ,∠COB= .
11.(4分)如图, 于 , ,则 的度数是
12.(4分)(2020七下·麻城期末)如图,直线 , 相交于点 , , ,则 度.
三、解答题(共6题;共54分)
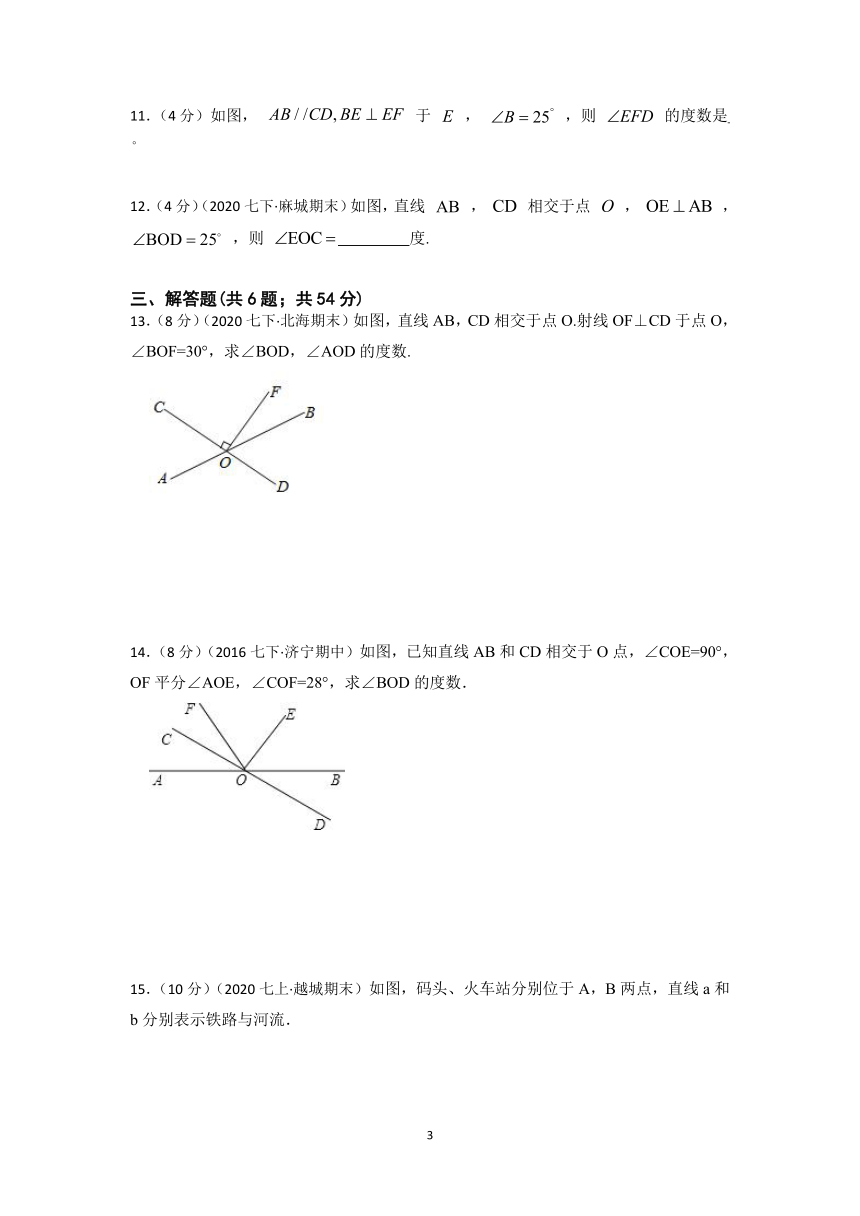
13.(8分)(2020七下·北海期末)如图,直线AB,CD相交于点O.射线OF⊥CD于点O,∠BOF=30°,求∠BOD,∠AOD的度数.
14.(8分)(2016七下·济宁期中)如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.
15.(10分)(2020七上·越城期末)如图,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)(4分)从码头A到火车站B怎样走最近,请画图并选择理由 ;(填入一个序号)
(2)(3分)从码头A到铁路a怎样走最近,请画图 并并选择理由 ;(填入一个序号)
①两点确定一条直线 ②两点之间线段最短 ③垂线段最短
16.(6分)(2019七上·江阴期末)如图,在直线MN的异侧有A、B两点,按要求画图取点,并注明画图取点的依据.
(1)(3分)在直线MN上取一点C,使线段AC最短.依据是 .
(2)(3分)在直线MN上取一点D,使线段AD+BD最短.依据是 .
17.(10分)(2019七下·江门期末)画图题,如图,已知三角形
(1)(5分)过点 作 ,点 为垂足
(2)(5分)在(1)的条件下,若 ,求点A到CD的距离
18.(12分)如图,已知OM,ON分别平分∠AOC、∠BOC,若∠MON=45°,则OA⊥OB,你能说明为什么吗?
答案部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】C
7.【答案】55°
8.【答案】40
9.【答案】垂线段最短
10.【答案】64°;116°
11.【答案】65
12.【答案】65
13.【答案】解:∵OF⊥CD,
∴∠DOF=90°,
∵∠BOF=30°,
∴∠BOD=∠DOF-∠BOF=90°-30°=60°,
∵∠AOD+ ∠BOD= 180° ,
∴∠AOD=180°-∠BOD= 180°-60°=120°.
14.【答案】解:由角的和差,得∠EOF=∠COE﹣COF=90°﹣28°=62°.
由角平分线的性质,得∠AOF=∠EOF=62°.
由角的和差,得∠AOC=∠AOF﹣∠COF=62°﹣28°=34°.
由对顶角相等,得
∠BOD=∠AOC=34°.
15.【答案】(1)②
(2);③
16.【答案】(1)垂线段最短
(2)两点之间,线段最短
17.【答案】(1)解:如图,CD为所作.
(2)解:∵AB=5,BD=2,
∴AD=3,
∴点A到CD的距离为3.
18.【答案】解:∵OM、ON分别平分∠AOC、∠BOC,
∴∠AOC=2∠COM,∠BOC=2∠CON,
∴∠AOB=∠AOC﹣∠BOC
=2(∠COM﹣∠CON)
=2∠MON
=90°,
∴OA⊥OB.2
第1周限时作业(基础)(5.1相交线)(含答案)
一、单选题(共6题;共18分)
1.(3分)(2018七下·钦州期末)如图,已知∠1=120°,则∠2的度数是( )
A.120° B.90° C.60° D.30°
2.(3分)(2020七上·扬州期末)点P为直线外一点,点A、B在直线l上,若PA=4cm,PB=5cm,则点P到直线l的距离是( )
A.4cm B.小于4cm C.不大于4cm D.5cm
3.(3分)(2021七下·娄星期末)如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是( )
A.6 B.8 C.10 D.4.8
4.(3分)(2021七下·涵江期末)如图,点A、C、B在同一直线上,DC⊥EC,若∠BCD=40°,则∠ACE的度数是( )
A.30° B.40° C.50° D.60°
5.(3分)(2020七下·余杭期末)如图,射线AB,AC被射线DE所截,图中的∠1与∠2是( )
A.内错角 B.对顶角 C.同位角 D.同旁内角
6.(3分)(2021七下·凤山月考)如图,在线段PA,PB,PC,PD中,长度最小的是( )
A.线段PA B.线段 PC C.线段PB D.线段PD
二、填空题(共6题;共28分)
7.(4分)(2019七下·大石桥期中)如图,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,则∠DOG= .
8.(4分)(2021七下·黄陂期末)如图,直线 , 相交于点 , ,若 ,则 的度数为 °.
9.(4分)(2021七下·海淀期中)如图,要在河岸l上建一个水泵房D,修建引水渠到村庄C处.施工人员的做法是:过点C作 于点D,将水泵房建在了D处.这样修建引水渠 最短,既省人力又省物力,这样做蕴含的数学原理是 .
10.(8分)(2020七下·徽县期末)如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC= ,∠COB= .
11.(4分)如图, 于 , ,则 的度数是
12.(4分)(2020七下·麻城期末)如图,直线 , 相交于点 , , ,则 度.
三、解答题(共6题;共54分)
13.(8分)(2020七下·北海期末)如图,直线AB,CD相交于点O.射线OF⊥CD于点O,∠BOF=30°,求∠BOD,∠AOD的度数.
14.(8分)(2016七下·济宁期中)如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.
15.(10分)(2020七上·越城期末)如图,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)(4分)从码头A到火车站B怎样走最近,请画图并选择理由 ;(填入一个序号)
(2)(3分)从码头A到铁路a怎样走最近,请画图 并并选择理由 ;(填入一个序号)
①两点确定一条直线 ②两点之间线段最短 ③垂线段最短
16.(6分)(2019七上·江阴期末)如图,在直线MN的异侧有A、B两点,按要求画图取点,并注明画图取点的依据.
(1)(3分)在直线MN上取一点C,使线段AC最短.依据是 .
(2)(3分)在直线MN上取一点D,使线段AD+BD最短.依据是 .
17.(10分)(2019七下·江门期末)画图题,如图,已知三角形
(1)(5分)过点 作 ,点 为垂足
(2)(5分)在(1)的条件下,若 ,求点A到CD的距离
18.(12分)如图,已知OM,ON分别平分∠AOC、∠BOC,若∠MON=45°,则OA⊥OB,你能说明为什么吗?
答案部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】C
7.【答案】55°
8.【答案】40
9.【答案】垂线段最短
10.【答案】64°;116°
11.【答案】65
12.【答案】65
13.【答案】解:∵OF⊥CD,
∴∠DOF=90°,
∵∠BOF=30°,
∴∠BOD=∠DOF-∠BOF=90°-30°=60°,
∵∠AOD+ ∠BOD= 180° ,
∴∠AOD=180°-∠BOD= 180°-60°=120°.
14.【答案】解:由角的和差,得∠EOF=∠COE﹣COF=90°﹣28°=62°.
由角平分线的性质,得∠AOF=∠EOF=62°.
由角的和差,得∠AOC=∠AOF﹣∠COF=62°﹣28°=34°.
由对顶角相等,得
∠BOD=∠AOC=34°.
15.【答案】(1)②
(2);③
16.【答案】(1)垂线段最短
(2)两点之间,线段最短
17.【答案】(1)解:如图,CD为所作.
(2)解:∵AB=5,BD=2,
∴AD=3,
∴点A到CD的距离为3.
18.【答案】解:∵OM、ON分别平分∠AOC、∠BOC,
∴∠AOC=2∠COM,∠BOC=2∠CON,
∴∠AOB=∠AOC﹣∠BOC
=2(∠COM﹣∠CON)
=2∠MON
=90°,
∴OA⊥OB.2
