等比数列同步试题汇编-北京市2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册(word版含答案)
文档属性
| 名称 | 等比数列同步试题汇编-北京市2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 660.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 00:00:00 | ||
图片预览

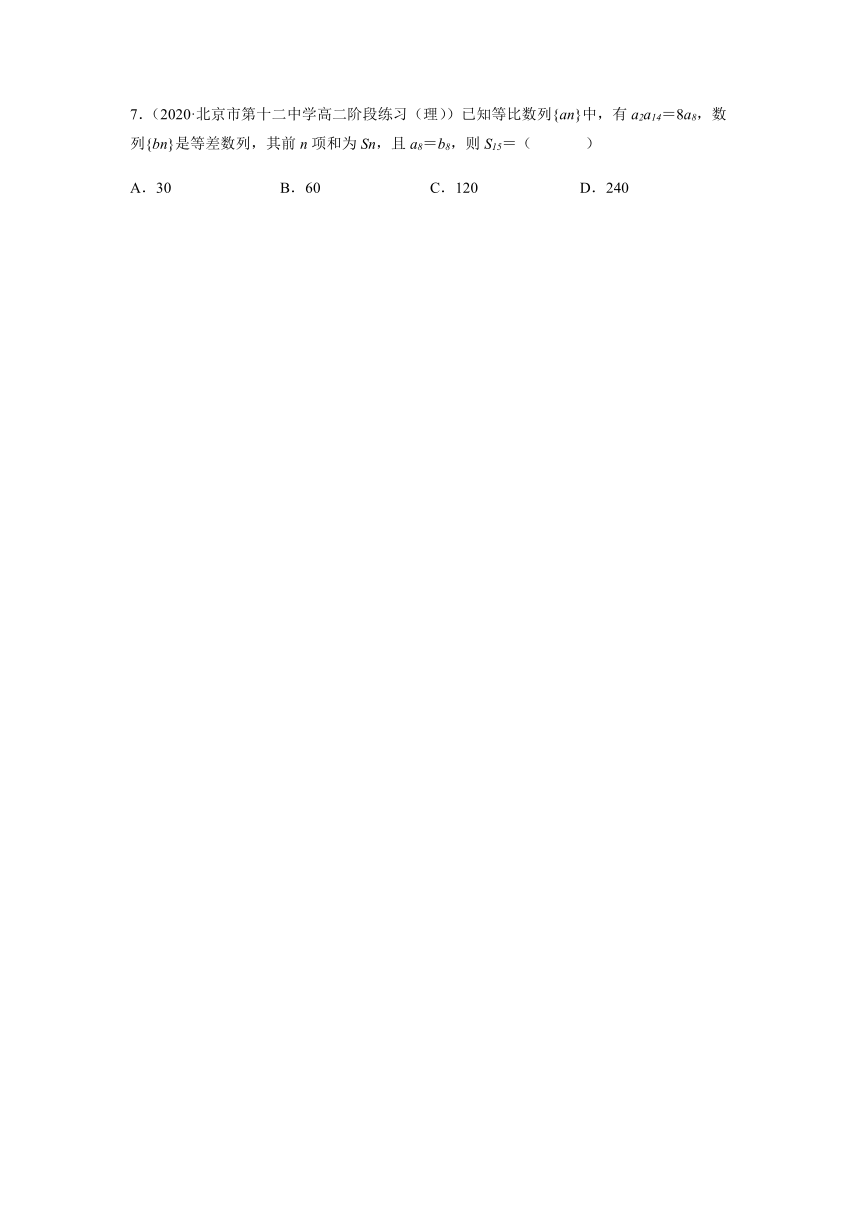



文档简介
2022高二同步汇编---等比数列
一、选择题
1.(2022·北京·首师大附属丽泽中学高二期末)等比数列的公比,.则( )
A. B. C. D.
2.(2022·北京师大附中高二期末)已知等比数列的公比为q.若为递增数列且,则( )
A. B. C. D.
3.(2021·北京·清华附中高二期中)已知等比数列的各项均为正数,且,则( )
A. B.5 C.10 D.15
4.(2019·北京一七一中高二阶段练习)设等比数列的公比,前项和为,则( )
A. B. C. D.
5.(2021·北京朝阳·高二期末)光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置.表达光圈的大小我们可以用光圈的F值表示,光圈的F值系列如下:F1,F1.4,F2,F2.8,F4,F5.6,F8,…,F64.光圈的F值越小,表示在同一单位时间内进光量越多,而且上一级的进光量是下一级的2倍,如光圈从F8调整到F5.6,进光量是原来的2倍.若光圈从F4调整到F1.4,则单位时间内的进光量为原来的( )
A.2倍 B.4倍 C.8倍 D.16倍
6.(2020·北京市第一六六中学高二期中)等比数列{an},a1=33,q=,设前n项的积Tn=,则当n=_____时,Tn取得最大值. ( )
A.6 B.7 C.8 D.9
7.(2020·北京市第十二中学高二阶段练习(理))已知等比数列{an}中,有a2a14=8a8,数列{bn}是等差数列,其前n项和为Sn,且a8=b8,则S15=( )
A.30 B.60 C.120 D.240
8.(2020·北京·清华附中高二期中)等差数列的首项为,公差不为若,,成等比数列,则的前项和为( )
A. B. C. D.
9.(2022·北京师大附中高二期末)已知数列为等比数列,则“为常数列”是“成等差数列”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
10.(2019·北京四中高二期中)设是等差数列,为等比数列,其公比, 且,若,,则与的大小关系为
A. B. C. D.不确定
二、填空题
11.(2021·北京·101中学高二期中)设数列为等比数列,其公比为,已知,,则___________·
12.(2021·北京海淀·高二期中)已知等比数列满足能说明“若,则”为假命题的数列的通项公式__________.(写出一个即可)
13.(2019·北京·昌平一中高二期中)已知是公比为2的等比数列,若,则___________;___________.
14.(2021·北京·东直门中学高二阶段练习)设Sn为公比q≠1的等比数列{an}的前n项和,且3a1,2a2,a3成等差数列,则q=_____,_____.
15.(2019·北京市八一中学高二期中)等比数列的前项和记为,满足,,,,则的值为______.
三、解答题
16.(2020·北京·北大附中高二期末)在等比数列{an}中,a2=1,a5=8,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若Sn<100,求n的最大值.
17.(2019·北京·昌平一中高二期中)设是等差数列,是各项都为正数的等比数列,且,,.
(1)求,的通项公式;
(2)求数列的前项和.
18.(2020·北京延庆·高二期中)已知是等差数列,是等比数列,且,,,成等比数列,,.
(1)求的通项公式和的前项和及的最小值;
(2)求和:.
19.(2020·北京·清华附中高二期中)设为等比数列的前项和,已知满足______,求公比以及.
从①且,②且,③且这三组条件中任选一组,补充到上面问题中,并完成解答.
20.(2021·北京·东直门中学高二阶段练习)已知{an}(n∈N*)是各项均为正数的等比数列,a1=16,2a3+3a2=32.
(1)求{an}的通项公式;
(2)设bn=log2an,求证:数列{bn}是等差数列;
(3)若数列{bn}的前n项和Sn,求Sn的最大值.
21.(2021·北京市第四十三中学高二阶段练习)设是等差数列,,且,,成等比数列.
(1)求的通项公式.
(2)记的前项和为,求的最小值.
(3)记的前项和为,求的表达式.
2022高二同步汇编---等比数列
一、选择题
1.(2022·北京·首师大附属丽泽中学高二期末)等比数列的公比,.则( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据等比数列通项公式求项即可.
【详解】
由题设,.
故选:B
2.(2022·北京师大附中高二期末)已知等比数列的公比为q.若为递增数列且,则( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据题设等比数列的性质,结合等比数列通项公式确定公比的范围即可.
【详解】
由题意,,又,
∴要使为递增数列,则,
当时,为递增数列,符合题设;
当时,为递减数列,符合题设;
故选:C.
3.(2021·北京·清华附中高二期中)已知等比数列的各项均为正数,且,则( )
A. B.5 C.10 D.15
【答案】B
【解析】
【分析】
利用等比中项和对数的运算性质可求得结果.
【详解】
因为等比数列的各项均为正数,且,
所以.
故选:B.
4.(2019·北京一七一中高二阶段练习)设等比数列的公比,前项和为,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
利用等比数列的通项公式与求和公式即可得出.
【详解】
设数列的首项为.
∵数列为等比数列,且公比
∴,,且
∴
故选:B.
5.(2021·北京朝阳·高二期末)光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置.表达光圈的大小我们可以用光圈的F值表示,光圈的F值系列如下:F1,F1.4,F2,F2.8,F4,F5.6,F8,…,F64.光圈的F值越小,表示在同一单位时间内进光量越多,而且上一级的进光量是下一级的2倍,如光圈从F8调整到F5.6,进光量是原来的2倍.若光圈从F4调整到F1.4,则单位时间内的进光量为原来的( )
A.2倍 B.4倍 C.8倍 D.16倍
【答案】C
【解析】
【分析】
由题可得单位时间内的进光量形成公比为的等比数列,即可求得.
【详解】
由题可得单位时间内的进光量形成公比为的等比数列,
则F4对应单位时间内的进光量为,F1.4对应单位时间内的进光量为,
从F4调整到F1.4,则单位时间内的进光量为原来的倍.
故选:C.
6.(2020·北京市第一六六中学高二期中)等比数列{an},a1=33,q=,设前n项的积Tn=,则当n=_____时,Tn取得最大值. ( )
A.6 B.7 C.8 D.9
【答案】A
【解析】
【分析】
利用等比数列的通项公式代入即可求解.
【详解】
由{an}是等比数列,a1=33,q=,
所以,且数列为递减数列,
由,,
所以前n项的积Tn=,
当时,Tn取得最大值.
故选:A.
【点睛】
本题考查了等比数列的通项公式,考查了基本运算,需熟记公式,属于基础题.
7.(2020·北京市第十二中学高二阶段练习(理))已知等比数列{an}中,有a2a14=8a8,数列{bn}是等差数列,其前n项和为Sn,且a8=b8,则S15=( )
A.30 B.60 C.120 D.240
【答案】C
【解析】
【分析】
由等比数列的中项性质可得a8=8,设等差数列的公差为d,运用等差数列的通项公式和求和公式,计算可得所求和.
【详解】
等比数列{an}中,有a2a14=8a8,可得a82=8a8,解得a8=8(0舍去),
数列{bn}是等差数列,设公差为d,其前n项和为Sn,
由a8=b8=8,可得b1+7d=8,
则S15=15b115×14d=15(b1+7d)=15×8=120.
故选:C.
【点睛】
本题考查等比数列的中项性质和等差数列的通项公式、求和公式的运用,考查方程思想和运算能力,属于基础题.
8.(2020·北京·清华附中高二期中)等差数列的首项为,公差不为若,,成等比数列,则的前项和为( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据题意,求出公差,代入等差数列的前项和公式即可得解.
【详解】
由题意,设等差数列的公差为,,
又,
,,成等比数列,
,
,
解得,
则的前项和为:.
故选:A.
9.(2022·北京师大附中高二期末)已知数列为等比数列,则“为常数列”是“成等差数列”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】C
【解析】
【分析】
先考虑充分性,再考虑必要性即得解.
【详解】
解:如果为常数列,则成等差数列,所以“为常数列”是“成等差数列”的充分条件;
等差数列,所以,所以数列为,
所以数列是常数列,所以“为常数列”是“成等差数列”的必要条件.
所以“为常数列”是“成等差数列”的充要条件.
故选:C
10.(2019·北京四中高二期中)设是等差数列,为等比数列,其公比, 且,若,,则与的大小关系为
A. B. C. D.不确定
【答案】B
【解析】
【分析】
根据等差中项和等比中项的性质,结合基本不等式,判断出与的大小关系.
【详解】
由于是等差数列,为等比数列,所以,而,,所以,由于,根据基本不等式可知,即.
故选B.
【点睛】
本小题主要考查等差中项、等比中项的性质,考查基本不等式求最值.
二、填空题
11.(2021·北京·101中学高二期中)设数列为等比数列,其公比为,已知,,则___________·
【答案】
【解析】
【分析】
利用等比数列的求和公式即可得出.
【详解】
解:,,
,,
解得,
所以.
故答案为:.
12.(2021·北京海淀·高二期中)已知等比数列满足能说明“若,则”为假命题的数列的通项公式__________.(写出一个即可)
【答案】
【解析】
【分析】
根据给定条件探求出等比数列公比q具有的性质,再分情况讨论即得.
【详解】
设等比数列公比,由得,而,于是得,即或,
当时,,则,“若,则为真命题,与题设矛盾,
当时,因不成立,则必有,而,必有,
取,则,
此时,而,,即“若,则”为假命题,
所以等比数列的通项公式可以为.
故答案为:
13.(2019·北京·昌平一中高二期中)已知是公比为2的等比数列,若,则___________;___________.
【答案】 2
【解析】
【分析】
利用等比数列的通项公式求出,再求出代入化简,代入,结合等比数列的前项和公式求解.
【详解】
由题意知,则,
因为,可得,所以,所以,
则,
故答案为:2,.
14.(2021·北京·东直门中学高二阶段练习)设Sn为公比q≠1的等比数列{an}的前n项和,且3a1,2a2,a3成等差数列,则q=_____,_____.
【答案】 3 10
【解析】
【分析】
利用等差数列的中项性质和等比数列的通项公式求出公比q,再利用等比数列的求和公式即可求解.
【详解】
Sn为公比q≠1的等比数列{an}的前n项和,且3a1,2a2,a3成等差数列,
可得4a2=3a1+a3,
即有4a1q=3a1+a1q2,
即q2﹣4q+3=0,解得q=3,
故,,
则.
故答案为:3;10.
15.(2019·北京市八一中学高二期中)等比数列的前项和记为,满足,,,,则的值为______.
【答案】5
【解析】
【分析】
先求出进而可得数列的公比,再根据等比数列的基本量,列出方程组即可求得.
【详解】
因为,,,
故可得,
则数列的公比.
则由,
可得,
则,
当为偶数时,解得,显然无解;
当为奇数时,解得,解得.
故答案为:5.
【点睛】
本题考查等比数列基本量的求解,属基础题.
三、解答题
16.(2020·北京·北大附中高二期末)在等比数列{an}中,a2=1,a5=8,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若Sn<100,求n的最大值.
【答案】(1)an=2n﹣2;
(2)n=7.
【解析】
【分析】
(1)由已知结合等比数控的性质可求公比q,然后结合通项公式即可求解;
(2)结合等比数列的通项公式,即可求解n.
(1)
因为a2=1,a5=8,
所以q3==8,故q=2,则
(2)
Sn==<100,
则2n<201,
由于27=128,28=256
满足条件的n=7.
17.(2019·北京·昌平一中高二期中)设是等差数列,是各项都为正数的等比数列,且,,.
(1)求,的通项公式;
(2)求数列的前项和.
【答案】(1),;(2).
【解析】
【分析】
(1)设是公差为的等差数列,是各项都为正数,公比为的等比数列,运用等比数列和等差数列的通项公式,解方程可得和,进而得到所求通项公式;
(2),运用数列的求和方法:分组求和,结合等差数列和等比数列的求和公式,即可得到所求和.
【详解】
解:(1)设的公差为,的公比为,
则,,,即为,
,
解得,
可得;;
(2),
前项和为
.
18.(2020·北京延庆·高二期中)已知是等差数列,是等比数列,且,,,成等比数列,,.
(1)求的通项公式和的前项和及的最小值;
(2)求和:.
【答案】(1),,-9;(2).
【解析】
【分析】
(1)设是公差为的等差数列,由等比中项和等差数列的通项公式,解方程可得公差,进而得到所求通项公式和,再由配方可得所求最小值;
(2)设是公比为的等比数列,由等比数列的通项公式可得的奇数项是首项为1,公比为3的等比数列,再由等比数列的求和公式计算可得所求和.
【详解】
解:(1)设是公差为的等差数列,
由,,,成等比数列,可得,
即,
解得,则,
,
当时,取得最小值﹣9.
(2)设是公比为的等比数列,
由,,即,可得,
由的奇数项是首项为1,公比为3的等比数列,
可得.
19.(2020·北京·清华附中高二期中)设为等比数列的前项和,已知满足______,求公比以及.
从①且,②且,③且这三组条件中任选一组,补充到上面问题中,并完成解答.
【答案】答案不唯一,具体见解析
【解析】
若选①,根据等比数列的性质得出,结合,联立方程组求出和,从而求出或,进而算出对应的,结合是以为首项,为公比的等比数列,利用等比数列求和公式,即可求出;
若选②,由于且,可求出,结合是以为首项,为公比的等比数列,利用等比数列求和公式,即可求出;
若选③,根据且,利用等比数列的性质,即可求出,进而求得,结合是以为首项,为公比的等比数列,利用等比数列求和公式,即可求出.
【详解】
解:若选①,则有,
故有,得或,
即或.
因为是以为首项,为公比的等比数列,
若,,此时;
或,,此时;
若选②,,即,故,
因为是以为首项,为公比的等比数列,
所以;
若选③,(*),(**),
令(**)式减(*)式,得,
即,故,
则(*)式中,,
即,即,
因为是以为首项,为公比的等比数列,
所以.
【点睛】
本题考查利用等比数列的通项公式求出基本量,以及等比数列的求和公式,还涉及等比数列的性质,考查计算能力.
20.(2021·北京·东直门中学高二阶段练习)已知{an}(n∈N*)是各项均为正数的等比数列,a1=16,2a3+3a2=32.
(1)求{an}的通项公式;
(2)设bn=log2an,求证:数列{bn}是等差数列;
(3)若数列{bn}的前n项和Sn,求Sn的最大值.
【答案】(1);(2)证明见解析;(3)10.
【解析】
【分析】
(1)设等比数列{an}的公比为q(q>0),利用a1=16,2a3+3a2=32求出q值后,即可得到{an}的通项公式;(2)由(1)可知bn=log22﹣n+5=﹣n+5,然后利用等差数列的定义即可求解;(3)利用(2)中结论,并结合二次函数的性质即可求出Sn的最大值.
【详解】
(1)设等比数列{an}的公比为q(q>0),
由2a3+3a2=32,得2a1q2+3a1q=32,又a1=16,得2q2+3q﹣2=0,解得,
所以;
(2)证明:由(1)可知,
则当n=1时,b1=4,且,
所以bn+1﹣bn=﹣n+4﹣(﹣n+5)=﹣1,
故数列{bn}是以4为首项,﹣1为公差的等差数列;
(3),
故当n=4或5时,Sn有最大值,且最大值为S4=S5=10.
21.(2021·北京市第四十三中学高二阶段练习)设是等差数列,,且,,成等比数列.
(1)求的通项公式.
(2)记的前项和为,求的最小值.
(3)记的前项和为,求的表达式.
【答案】(1);(2);(3)
【解析】
【分析】
(1)利用等差数列的通项公式以及等比数列的性质列方程求出的公差即可求解;
(2)由等差数列的求和公式求出,再利用二次函数的性质即可求解;
(3)讨论当时,,;当时,,,写成分段的形式即可.
【详解】
(1)设的公差为,因为,,成等比数列,
所以,即,
所以,所以,解得:,
所以,
(2)由(1)知:,所以,
所以当或时,取得最小值为;
(3)当时,,此时,
,
当时,,此时,
,
综上所述:.
一、选择题
1.(2022·北京·首师大附属丽泽中学高二期末)等比数列的公比,.则( )
A. B. C. D.
2.(2022·北京师大附中高二期末)已知等比数列的公比为q.若为递增数列且,则( )
A. B. C. D.
3.(2021·北京·清华附中高二期中)已知等比数列的各项均为正数,且,则( )
A. B.5 C.10 D.15
4.(2019·北京一七一中高二阶段练习)设等比数列的公比,前项和为,则( )
A. B. C. D.
5.(2021·北京朝阳·高二期末)光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置.表达光圈的大小我们可以用光圈的F值表示,光圈的F值系列如下:F1,F1.4,F2,F2.8,F4,F5.6,F8,…,F64.光圈的F值越小,表示在同一单位时间内进光量越多,而且上一级的进光量是下一级的2倍,如光圈从F8调整到F5.6,进光量是原来的2倍.若光圈从F4调整到F1.4,则单位时间内的进光量为原来的( )
A.2倍 B.4倍 C.8倍 D.16倍
6.(2020·北京市第一六六中学高二期中)等比数列{an},a1=33,q=,设前n项的积Tn=,则当n=_____时,Tn取得最大值. ( )
A.6 B.7 C.8 D.9
7.(2020·北京市第十二中学高二阶段练习(理))已知等比数列{an}中,有a2a14=8a8,数列{bn}是等差数列,其前n项和为Sn,且a8=b8,则S15=( )
A.30 B.60 C.120 D.240
8.(2020·北京·清华附中高二期中)等差数列的首项为,公差不为若,,成等比数列,则的前项和为( )
A. B. C. D.
9.(2022·北京师大附中高二期末)已知数列为等比数列,则“为常数列”是“成等差数列”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
10.(2019·北京四中高二期中)设是等差数列,为等比数列,其公比, 且,若,,则与的大小关系为
A. B. C. D.不确定
二、填空题
11.(2021·北京·101中学高二期中)设数列为等比数列,其公比为,已知,,则___________·
12.(2021·北京海淀·高二期中)已知等比数列满足能说明“若,则”为假命题的数列的通项公式__________.(写出一个即可)
13.(2019·北京·昌平一中高二期中)已知是公比为2的等比数列,若,则___________;___________.
14.(2021·北京·东直门中学高二阶段练习)设Sn为公比q≠1的等比数列{an}的前n项和,且3a1,2a2,a3成等差数列,则q=_____,_____.
15.(2019·北京市八一中学高二期中)等比数列的前项和记为,满足,,,,则的值为______.
三、解答题
16.(2020·北京·北大附中高二期末)在等比数列{an}中,a2=1,a5=8,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若Sn<100,求n的最大值.
17.(2019·北京·昌平一中高二期中)设是等差数列,是各项都为正数的等比数列,且,,.
(1)求,的通项公式;
(2)求数列的前项和.
18.(2020·北京延庆·高二期中)已知是等差数列,是等比数列,且,,,成等比数列,,.
(1)求的通项公式和的前项和及的最小值;
(2)求和:.
19.(2020·北京·清华附中高二期中)设为等比数列的前项和,已知满足______,求公比以及.
从①且,②且,③且这三组条件中任选一组,补充到上面问题中,并完成解答.
20.(2021·北京·东直门中学高二阶段练习)已知{an}(n∈N*)是各项均为正数的等比数列,a1=16,2a3+3a2=32.
(1)求{an}的通项公式;
(2)设bn=log2an,求证:数列{bn}是等差数列;
(3)若数列{bn}的前n项和Sn,求Sn的最大值.
21.(2021·北京市第四十三中学高二阶段练习)设是等差数列,,且,,成等比数列.
(1)求的通项公式.
(2)记的前项和为,求的最小值.
(3)记的前项和为,求的表达式.
2022高二同步汇编---等比数列
一、选择题
1.(2022·北京·首师大附属丽泽中学高二期末)等比数列的公比,.则( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据等比数列通项公式求项即可.
【详解】
由题设,.
故选:B
2.(2022·北京师大附中高二期末)已知等比数列的公比为q.若为递增数列且,则( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据题设等比数列的性质,结合等比数列通项公式确定公比的范围即可.
【详解】
由题意,,又,
∴要使为递增数列,则,
当时,为递增数列,符合题设;
当时,为递减数列,符合题设;
故选:C.
3.(2021·北京·清华附中高二期中)已知等比数列的各项均为正数,且,则( )
A. B.5 C.10 D.15
【答案】B
【解析】
【分析】
利用等比中项和对数的运算性质可求得结果.
【详解】
因为等比数列的各项均为正数,且,
所以.
故选:B.
4.(2019·北京一七一中高二阶段练习)设等比数列的公比,前项和为,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
利用等比数列的通项公式与求和公式即可得出.
【详解】
设数列的首项为.
∵数列为等比数列,且公比
∴,,且
∴
故选:B.
5.(2021·北京朝阳·高二期末)光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置.表达光圈的大小我们可以用光圈的F值表示,光圈的F值系列如下:F1,F1.4,F2,F2.8,F4,F5.6,F8,…,F64.光圈的F值越小,表示在同一单位时间内进光量越多,而且上一级的进光量是下一级的2倍,如光圈从F8调整到F5.6,进光量是原来的2倍.若光圈从F4调整到F1.4,则单位时间内的进光量为原来的( )
A.2倍 B.4倍 C.8倍 D.16倍
【答案】C
【解析】
【分析】
由题可得单位时间内的进光量形成公比为的等比数列,即可求得.
【详解】
由题可得单位时间内的进光量形成公比为的等比数列,
则F4对应单位时间内的进光量为,F1.4对应单位时间内的进光量为,
从F4调整到F1.4,则单位时间内的进光量为原来的倍.
故选:C.
6.(2020·北京市第一六六中学高二期中)等比数列{an},a1=33,q=,设前n项的积Tn=,则当n=_____时,Tn取得最大值. ( )
A.6 B.7 C.8 D.9
【答案】A
【解析】
【分析】
利用等比数列的通项公式代入即可求解.
【详解】
由{an}是等比数列,a1=33,q=,
所以,且数列为递减数列,
由,,
所以前n项的积Tn=,
当时,Tn取得最大值.
故选:A.
【点睛】
本题考查了等比数列的通项公式,考查了基本运算,需熟记公式,属于基础题.
7.(2020·北京市第十二中学高二阶段练习(理))已知等比数列{an}中,有a2a14=8a8,数列{bn}是等差数列,其前n项和为Sn,且a8=b8,则S15=( )
A.30 B.60 C.120 D.240
【答案】C
【解析】
【分析】
由等比数列的中项性质可得a8=8,设等差数列的公差为d,运用等差数列的通项公式和求和公式,计算可得所求和.
【详解】
等比数列{an}中,有a2a14=8a8,可得a82=8a8,解得a8=8(0舍去),
数列{bn}是等差数列,设公差为d,其前n项和为Sn,
由a8=b8=8,可得b1+7d=8,
则S15=15b115×14d=15(b1+7d)=15×8=120.
故选:C.
【点睛】
本题考查等比数列的中项性质和等差数列的通项公式、求和公式的运用,考查方程思想和运算能力,属于基础题.
8.(2020·北京·清华附中高二期中)等差数列的首项为,公差不为若,,成等比数列,则的前项和为( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据题意,求出公差,代入等差数列的前项和公式即可得解.
【详解】
由题意,设等差数列的公差为,,
又,
,,成等比数列,
,
,
解得,
则的前项和为:.
故选:A.
9.(2022·北京师大附中高二期末)已知数列为等比数列,则“为常数列”是“成等差数列”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】C
【解析】
【分析】
先考虑充分性,再考虑必要性即得解.
【详解】
解:如果为常数列,则成等差数列,所以“为常数列”是“成等差数列”的充分条件;
等差数列,所以,所以数列为,
所以数列是常数列,所以“为常数列”是“成等差数列”的必要条件.
所以“为常数列”是“成等差数列”的充要条件.
故选:C
10.(2019·北京四中高二期中)设是等差数列,为等比数列,其公比, 且,若,,则与的大小关系为
A. B. C. D.不确定
【答案】B
【解析】
【分析】
根据等差中项和等比中项的性质,结合基本不等式,判断出与的大小关系.
【详解】
由于是等差数列,为等比数列,所以,而,,所以,由于,根据基本不等式可知,即.
故选B.
【点睛】
本小题主要考查等差中项、等比中项的性质,考查基本不等式求最值.
二、填空题
11.(2021·北京·101中学高二期中)设数列为等比数列,其公比为,已知,,则___________·
【答案】
【解析】
【分析】
利用等比数列的求和公式即可得出.
【详解】
解:,,
,,
解得,
所以.
故答案为:.
12.(2021·北京海淀·高二期中)已知等比数列满足能说明“若,则”为假命题的数列的通项公式__________.(写出一个即可)
【答案】
【解析】
【分析】
根据给定条件探求出等比数列公比q具有的性质,再分情况讨论即得.
【详解】
设等比数列公比,由得,而,于是得,即或,
当时,,则,“若,则为真命题,与题设矛盾,
当时,因不成立,则必有,而,必有,
取,则,
此时,而,,即“若,则”为假命题,
所以等比数列的通项公式可以为.
故答案为:
13.(2019·北京·昌平一中高二期中)已知是公比为2的等比数列,若,则___________;___________.
【答案】 2
【解析】
【分析】
利用等比数列的通项公式求出,再求出代入化简,代入,结合等比数列的前项和公式求解.
【详解】
由题意知,则,
因为,可得,所以,所以,
则,
故答案为:2,.
14.(2021·北京·东直门中学高二阶段练习)设Sn为公比q≠1的等比数列{an}的前n项和,且3a1,2a2,a3成等差数列,则q=_____,_____.
【答案】 3 10
【解析】
【分析】
利用等差数列的中项性质和等比数列的通项公式求出公比q,再利用等比数列的求和公式即可求解.
【详解】
Sn为公比q≠1的等比数列{an}的前n项和,且3a1,2a2,a3成等差数列,
可得4a2=3a1+a3,
即有4a1q=3a1+a1q2,
即q2﹣4q+3=0,解得q=3,
故,,
则.
故答案为:3;10.
15.(2019·北京市八一中学高二期中)等比数列的前项和记为,满足,,,,则的值为______.
【答案】5
【解析】
【分析】
先求出进而可得数列的公比,再根据等比数列的基本量,列出方程组即可求得.
【详解】
因为,,,
故可得,
则数列的公比.
则由,
可得,
则,
当为偶数时,解得,显然无解;
当为奇数时,解得,解得.
故答案为:5.
【点睛】
本题考查等比数列基本量的求解,属基础题.
三、解答题
16.(2020·北京·北大附中高二期末)在等比数列{an}中,a2=1,a5=8,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若Sn<100,求n的最大值.
【答案】(1)an=2n﹣2;
(2)n=7.
【解析】
【分析】
(1)由已知结合等比数控的性质可求公比q,然后结合通项公式即可求解;
(2)结合等比数列的通项公式,即可求解n.
(1)
因为a2=1,a5=8,
所以q3==8,故q=2,则
(2)
Sn==<100,
则2n<201,
由于27=128,28=256
满足条件的n=7.
17.(2019·北京·昌平一中高二期中)设是等差数列,是各项都为正数的等比数列,且,,.
(1)求,的通项公式;
(2)求数列的前项和.
【答案】(1),;(2).
【解析】
【分析】
(1)设是公差为的等差数列,是各项都为正数,公比为的等比数列,运用等比数列和等差数列的通项公式,解方程可得和,进而得到所求通项公式;
(2),运用数列的求和方法:分组求和,结合等差数列和等比数列的求和公式,即可得到所求和.
【详解】
解:(1)设的公差为,的公比为,
则,,,即为,
,
解得,
可得;;
(2),
前项和为
.
18.(2020·北京延庆·高二期中)已知是等差数列,是等比数列,且,,,成等比数列,,.
(1)求的通项公式和的前项和及的最小值;
(2)求和:.
【答案】(1),,-9;(2).
【解析】
【分析】
(1)设是公差为的等差数列,由等比中项和等差数列的通项公式,解方程可得公差,进而得到所求通项公式和,再由配方可得所求最小值;
(2)设是公比为的等比数列,由等比数列的通项公式可得的奇数项是首项为1,公比为3的等比数列,再由等比数列的求和公式计算可得所求和.
【详解】
解:(1)设是公差为的等差数列,
由,,,成等比数列,可得,
即,
解得,则,
,
当时,取得最小值﹣9.
(2)设是公比为的等比数列,
由,,即,可得,
由的奇数项是首项为1,公比为3的等比数列,
可得.
19.(2020·北京·清华附中高二期中)设为等比数列的前项和,已知满足______,求公比以及.
从①且,②且,③且这三组条件中任选一组,补充到上面问题中,并完成解答.
【答案】答案不唯一,具体见解析
【解析】
若选①,根据等比数列的性质得出,结合,联立方程组求出和,从而求出或,进而算出对应的,结合是以为首项,为公比的等比数列,利用等比数列求和公式,即可求出;
若选②,由于且,可求出,结合是以为首项,为公比的等比数列,利用等比数列求和公式,即可求出;
若选③,根据且,利用等比数列的性质,即可求出,进而求得,结合是以为首项,为公比的等比数列,利用等比数列求和公式,即可求出.
【详解】
解:若选①,则有,
故有,得或,
即或.
因为是以为首项,为公比的等比数列,
若,,此时;
或,,此时;
若选②,,即,故,
因为是以为首项,为公比的等比数列,
所以;
若选③,(*),(**),
令(**)式减(*)式,得,
即,故,
则(*)式中,,
即,即,
因为是以为首项,为公比的等比数列,
所以.
【点睛】
本题考查利用等比数列的通项公式求出基本量,以及等比数列的求和公式,还涉及等比数列的性质,考查计算能力.
20.(2021·北京·东直门中学高二阶段练习)已知{an}(n∈N*)是各项均为正数的等比数列,a1=16,2a3+3a2=32.
(1)求{an}的通项公式;
(2)设bn=log2an,求证:数列{bn}是等差数列;
(3)若数列{bn}的前n项和Sn,求Sn的最大值.
【答案】(1);(2)证明见解析;(3)10.
【解析】
【分析】
(1)设等比数列{an}的公比为q(q>0),利用a1=16,2a3+3a2=32求出q值后,即可得到{an}的通项公式;(2)由(1)可知bn=log22﹣n+5=﹣n+5,然后利用等差数列的定义即可求解;(3)利用(2)中结论,并结合二次函数的性质即可求出Sn的最大值.
【详解】
(1)设等比数列{an}的公比为q(q>0),
由2a3+3a2=32,得2a1q2+3a1q=32,又a1=16,得2q2+3q﹣2=0,解得,
所以;
(2)证明:由(1)可知,
则当n=1时,b1=4,且,
所以bn+1﹣bn=﹣n+4﹣(﹣n+5)=﹣1,
故数列{bn}是以4为首项,﹣1为公差的等差数列;
(3),
故当n=4或5时,Sn有最大值,且最大值为S4=S5=10.
21.(2021·北京市第四十三中学高二阶段练习)设是等差数列,,且,,成等比数列.
(1)求的通项公式.
(2)记的前项和为,求的最小值.
(3)记的前项和为,求的表达式.
【答案】(1);(2);(3)
【解析】
【分析】
(1)利用等差数列的通项公式以及等比数列的性质列方程求出的公差即可求解;
(2)由等差数列的求和公式求出,再利用二次函数的性质即可求解;
(3)讨论当时,,;当时,,,写成分段的形式即可.
【详解】
(1)设的公差为,因为,,成等比数列,
所以,即,
所以,所以,解得:,
所以,
(2)由(1)知:,所以,
所以当或时,取得最小值为;
(3)当时,,此时,
,
当时,,此时,
,
综上所述:.
