华东师大版八年级下册数学 16.4.2 科学记数法 课件(共18张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 16.4.2 科学记数法 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 241.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 14:52:07 | ||
图片预览






文档简介
(共18张PPT)
科学记数法
学习目标
【教学目标】:
1、能较熟练地运用零指数幂与负整指数幂的性质进行有关计算。
2、会利用10的负整数次幂,用科学记数法表示一些绝对值较小的数。
【重点难点】:
重点:幂的性质(指数为全体整数)并会用于计算以及用科学记数法表示一些绝对值较小的数。
难点:理解和应用整数指数幂的性质。
一 、复习提问
1、
;
= ;
= ,
= ,
2、计算:
3、计算下列各式,并且把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3
探 索
科学记数法
1、回忆:用科学记数法表示一些绝对值较大的数,即利用10的正整数次幂,把一个绝对值大于10的数表示成 的形式,其中n是正整数,1≤∣a∣<10.
例如,864000可以写成8.64×105.
2、类似地,可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,将它们表示成 的形式,其中n是正整数,1≤∣a∣<10.
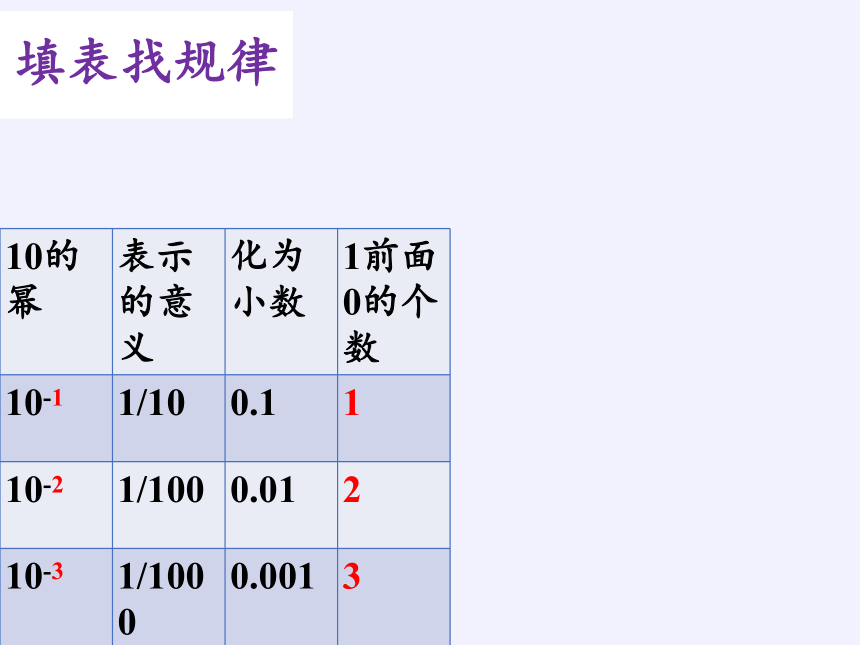
填表找规律
10的幂 表示的意义 化为小数 1前面0的个数
10-1 1/10 0.1 1
10-2 1/100 0.01 2
10-3 1/1000 0.001 3
10-4 1/10000 0.0001 4
总结规律
用科学记数法可以把一个绝对值小于1的非零数表示成±a×10-n其中1≤a≤10,n等于原数中的第一个非零数字前面所有零的个数(包括小数点前面的那个零).
比如,0.000001=1×10-6
0.0000023=2.3×10-6
-0.0000000352=-3.52×10-8
拓展训练
1. 用科学计数法表示下列各数:
(1)0.00002 (2)-0.0000307
(3)0.0031 (4)-0.00567
例题解析
例1 安哥拉长毛兔最细的兔毛直径约为5×10-6米,将这个数写成小数的形式。
解:5×10-6
= 5×0.000001
=0.000005(米)
2、将下列各数写成小数
(1)2×10-5 (2)-3.07×10-5
(3)3.1×10-3 (4)-5.67×10-3
例2、一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示.
分析:1纳米=
米.由
可知,1纳米=10-9米.
=10-9
解: 35纳米=35×10-9米.
而35×10-9=(3.5×10)×10-9
=35×101+(-9)=3.5×10-8,
答:这个纳米粒子的直径为3.5×10-8米.
做一做
用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=___秒;
(2)1毫克=_____千克;(3)1微米=_____米; (4)1纳米=_____微米;
(5)1平方厘米=_____平方米;
(6)1毫升=_________立方米.
例3. 一个氧原子的质量约为2.657×10-23克,一个氢原子的质量约为1.67×10-24克,一个氧原子的质量约为一个氢原子的质量的多少倍?
学习小结
1、你学到了哪些知识?要注意什么问题?
作业
课本P21练习第3题、习题16.4第3题、
P25第8题
附加:计算:
课堂练习
1、据报道,2006年全国高考报名总人数为9500000人,用科学记数法表示应为_________人。
2、据国家统计局统计,2006年第一季度国内生产总值约为43300亿元,用科学记数法表示为_________亿元。
3、先化简,再求值:
4、计算:
5、解方程:
06部分省市中考试题选
课堂练习
1、青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米。将2500000用科学记数法表示应为( )
A、0.25×107 B、2.5×107
C、2.5×106 D、25×105
C
2、已知 则 的值等于( )
A、6 B、-6 C、 2/15 D、-2/7
A
06部分省市中考试题选
谢 谢
科学记数法
学习目标
【教学目标】:
1、能较熟练地运用零指数幂与负整指数幂的性质进行有关计算。
2、会利用10的负整数次幂,用科学记数法表示一些绝对值较小的数。
【重点难点】:
重点:幂的性质(指数为全体整数)并会用于计算以及用科学记数法表示一些绝对值较小的数。
难点:理解和应用整数指数幂的性质。
一 、复习提问
1、
;
= ;
= ,
= ,
2、计算:
3、计算下列各式,并且把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3
探 索
科学记数法
1、回忆:用科学记数法表示一些绝对值较大的数,即利用10的正整数次幂,把一个绝对值大于10的数表示成 的形式,其中n是正整数,1≤∣a∣<10.
例如,864000可以写成8.64×105.
2、类似地,可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,将它们表示成 的形式,其中n是正整数,1≤∣a∣<10.
填表找规律
10的幂 表示的意义 化为小数 1前面0的个数
10-1 1/10 0.1 1
10-2 1/100 0.01 2
10-3 1/1000 0.001 3
10-4 1/10000 0.0001 4
总结规律
用科学记数法可以把一个绝对值小于1的非零数表示成±a×10-n其中1≤a≤10,n等于原数中的第一个非零数字前面所有零的个数(包括小数点前面的那个零).
比如,0.000001=1×10-6
0.0000023=2.3×10-6
-0.0000000352=-3.52×10-8
拓展训练
1. 用科学计数法表示下列各数:
(1)0.00002 (2)-0.0000307
(3)0.0031 (4)-0.00567
例题解析
例1 安哥拉长毛兔最细的兔毛直径约为5×10-6米,将这个数写成小数的形式。
解:5×10-6
= 5×0.000001
=0.000005(米)
2、将下列各数写成小数
(1)2×10-5 (2)-3.07×10-5
(3)3.1×10-3 (4)-5.67×10-3
例2、一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示.
分析:1纳米=
米.由
可知,1纳米=10-9米.
=10-9
解: 35纳米=35×10-9米.
而35×10-9=(3.5×10)×10-9
=35×101+(-9)=3.5×10-8,
答:这个纳米粒子的直径为3.5×10-8米.
做一做
用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=___秒;
(2)1毫克=_____千克;(3)1微米=_____米; (4)1纳米=_____微米;
(5)1平方厘米=_____平方米;
(6)1毫升=_________立方米.
例3. 一个氧原子的质量约为2.657×10-23克,一个氢原子的质量约为1.67×10-24克,一个氧原子的质量约为一个氢原子的质量的多少倍?
学习小结
1、你学到了哪些知识?要注意什么问题?
作业
课本P21练习第3题、习题16.4第3题、
P25第8题
附加:计算:
课堂练习
1、据报道,2006年全国高考报名总人数为9500000人,用科学记数法表示应为_________人。
2、据国家统计局统计,2006年第一季度国内生产总值约为43300亿元,用科学记数法表示为_________亿元。
3、先化简,再求值:
4、计算:
5、解方程:
06部分省市中考试题选
课堂练习
1、青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米。将2500000用科学记数法表示应为( )
A、0.25×107 B、2.5×107
C、2.5×106 D、25×105
C
2、已知 则 的值等于( )
A、6 B、-6 C、 2/15 D、-2/7
A
06部分省市中考试题选
谢 谢
