2022届高考数学冲刺课第9讲函数值域技巧、数形结合技巧课件(共61张PPT)
文档属性
| 名称 | 2022届高考数学冲刺课第9讲函数值域技巧、数形结合技巧课件(共61张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 22:50:26 | ||
图片预览










文档简介
(共61张PPT)
高考数学冲刺(9)
函数值域技巧、数形结合技巧
主讲人: |
2
01
椭圆
焦点三角形中的秒杀结论
02
椭圆
焦点、通径、渐近线秒杀技巧
03
椭圆
中点弦模型
04
函数
奇偶性、单调性、周期性秒杀技巧
05
综合
线性规划、二项式、不等式秒杀
06
数列
列举法秒杀数列
07
数列
数列四大求和方法
08
综合
排列组合七大解题策略
09
函数
函数值域技巧、数形结合技巧
10
综合
巧解高考小题
本节说明
求函数值域的常用方法:
1.换元法 2.分离常数法 3.基本不等式法
4.导数法 5.数形结合法 6.判别式法
7. 配方法 8. 单调性法 9.观察法
3
方法1
方法2
方法3
方法4
方法5
方法6
方法7
方法8
4
1.换元法
解题步骤:
第一步:观察函数解析式的形式,函数变量较多且相互关联;
第二步:另新元代换整体,得一新函数,求出新函数的值域即为原函数的值域.
1.求函数的值域.
方法1
5
例题
2.求函数的值域.
(1)对形如的函数,可以考虑换元,消掉根号,化成一个二次函数.
(2)在任何地方换元,都要注意新元的取值范围,它就是新函数的定义域.
(3)由于,所以当已知中同时又有的和或差的形式
以及积的形式,也可以考虑换元,化成二次函数.
方法1
6
例题
第二问经过一系列的推理化简得到,,求d的取值范围.
方法1
7
例题
解析: ,
令则
,易知在(1,]上是减函数,
所以
方法1
8
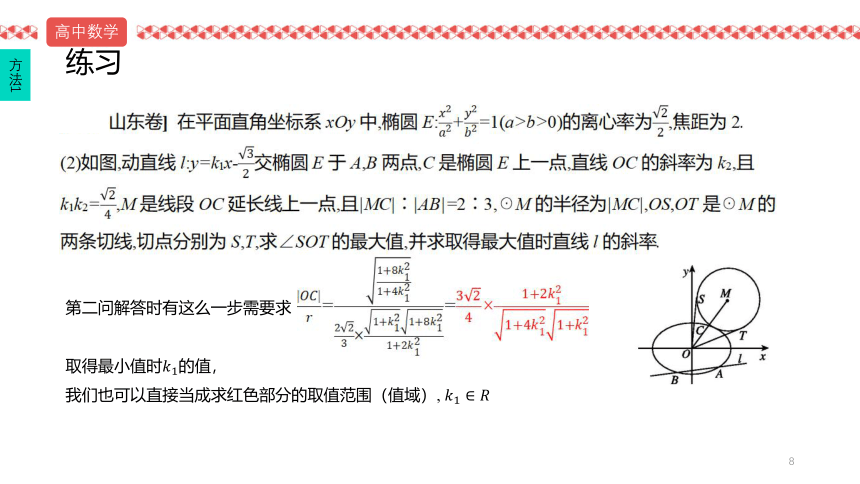
练习
第二问解答时有这么一步需要求
取得最小值时的值,
我们也可以直接当成求红色部分的取值范围(值域),
方法1
9
练习
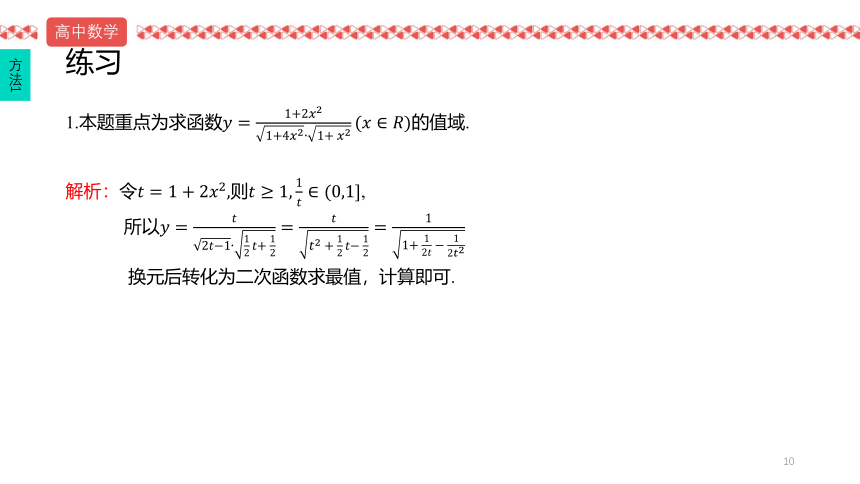
1.本题重点为求函数的值域.
方法1
10
练习
1.本题重点为求函数的值域.
解析:令则,
所以
换元后转化为二次函数求最值,计算即可.
方法1
11
2.分离常数法
解题步骤:
第一步:观察函数类型,型如;
第二步:对函数成形式;
第三步:求出函数在定义域范围内的值域,进而求函数的值域.
方法2
12
例题
1.函数,()的值域为 .
2.函数的值域为 .
方法2
13
3.基本不等式法
解题步骤:
第一步:观察函数解析式的形式,型如或的函数;
第二步:对函数进行配凑成形式,再利用基本不等式求函数的最值,
进而得到函数的值域.
方法3
例题
1.已知求函数的最小值.
2.求函数的最小值.
14
方法3
例题
1.已知求函数的最小值.
解析:因为所以
当且仅当 ,
即上式等号成立.
因为在定义域内,
所以最小值为1.
2.求函数的最小值.
解析:由题意得
+
当且仅当
即时等号成立.
所以函数最小值为
15
方法3
例题
3.(杭州模拟)已知实数若的值域为 .
方法3
例题
3.(杭州模拟)已知实数若的值域为 .
解析:
,其中,
所以
当且仅当等号成立,又当时, 取最大值,
故值域为[0,].
方法3
18
例题
4.(浙江卷)点P(0,-1)是椭圆C:的一个顶点,C的长轴是圆的直径,过点P且垂直的两条直线,其中交圆与A,B两点, 交椭圆于另一点D.
(2)求△ABD的面积取最大值时直线的方程.
第二问经过一系列的计算会得到,,求为何值时, 最大.
方法3
19
例题
解析:
当且仅当即或时等号成立.
方法3
20
练习
1.(湖北卷)已知F1,F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=,则椭圆和双曲线的离心率的倒数之和的最大值为 .
此题在第一讲中利用“交通线“秒杀结论来做的,较简单,若不用秒杀结论来做则会得到下面的式子:
假设离心率的倒数之和的平方为,则,,求其最大值.
方法3
21
练习
解析: ,
当即等号成立,
故最大值为离心率的倒数之和的最大值为.
方法3
22
练习
2.(全国II卷)设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个定点,直线与AB交于点D,与椭圆交于E,F两点.(2)求四边形AEBF面积的最大值.
第二问经过一系列的计算会得到,求其最值.
方法3
23
练习
解析,
当且仅当,即时取等号,
故四边形AEBF面积的最大值为.
方法3
24
4.数形结合法
1.求函数的值域.
2. 当,函数最小值为( )
A. 4 B. C.4 D.
方法4
25
例题
方法4
26
例题
3.对,记,函数的值域是 .
方法4
27
5.导数法
1.是抛物线C:上一点,A,B是C上的两点,线段AB被直线OM平分且P,求△ABP面积的最大.
此题在经过一系列的推理计算会得到,
,求最大值.
方法5
28
例题
解析:,
令 ,,则
令,则,
由0,所以
故△ABP面积的最大值为
方法5
求函数值域的常用方法:
1. 换元法 2. 分离常数法 3. 基本不等式法
4.导数法 5.数形结合法 6.判别式法
7. 配方法 8. 单调性法 9.观察法
当堂总结
以下内容为选讲内容,建议作为材料包
31
5.导数法
1.(浙江卷)已知P(2,1),不过原点O的直线l与椭圆C:交于A,B两点,且线段AB被直线OP平分.求△ABP的面积取最大时直线l的方程.
此题在经过一系列的推理计算会得到,
,求为值时,最大.
方法5
32
练习
解析:可以先求出面积的平方再开方来算. ,
令
求导得
,
因为,所以当时, 单调递增,
当时, 单调递减;
当= 时,△ABP的面积取得最大值.
方法5
3.不等式法
方法3
1.
在第二问中有 = ,求其范围.
34
3.不等式法
1.求函数, 的值域.
解析:令,,则
所以
又因为
所以值域为.
方法3
35
3.不等式法
2.已知椭圆C:l经过定点(0,2),且与椭圆C交于A,B两点,求△OAB面积的最大值.
经过一系列的计算会得到,,求△OAB面积的最大值.
方法3
36
练习
解析:,
当且仅当,即时等号成立,所以最大为1.
故△OAB面积的最大值为1.
方法3
3.
第二问经过一系列的计算会得到,求m的最大值可先求出最大值.
即求函数 的最大值.
37
3.不等式法
方法3
3.
第二问经过一系列的计算会得到,求m的最大值可先求出最大值.
即求函数 的最大值.
38
3.不等式法
解析:
令,则,
所以
当即时,取得最大值.
方法3
39
6.判别式法
解题步骤:
第一步:观察函数解析式的形式,型如的函数;
第二步:将函数式化成关于x的方程,且方程有解,用根的判别式求出参数y的取值范围,
即得函数的值域.
方法6
40
例题
1.求函数的值域.
2.求函数的值域.
方法6
41
例题
1.求函数的值域.
解析:因为2>0,所以函数的定义域为R.
原函数转化为
整理得
当时,上式可以看成关于的二次方程,时此方程有实数根,
即.
当时,方程为7=0,显然不成立,故,经检验时有解.
所以
方法6
42
7.配方法
1.(重庆)函数的最小值为 .
2.函数的值域为 .
方法7
43
例题
方法7
44
例题
方法7
45
8.单调性法
1.求函数的值域.
2.求函数的值域.
3.求函数的值域.
方法8
46
例题
4.求函数+的值域.
5.求函数的值域.
6.已知,则的最大值.
方法8
数形结合
1.数形结合的数学思想:包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:
一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,
比如应用函数的图象来直观地说明函数的性质;
二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,
如应用曲线的方程来精确地阐明曲线的几何性质.
数形结合
48
数形结合
2.数形结合思想解决的问题常有以下几种:
(1)构建函数模型并结合其图象求参数的取值范围.
(2)构建函数模型并结合其图象研究方程根的范围.
(3)构建函数模型并结合其图象研究量与量之间的大小关系.
(4)构建函数模型并结合其几何意义研究函数的最值问题和证明不等式.
(5)构建立体几何模型研究代数问题.
(6)构建解析几何中的斜率、截距、距离等模型研究最值问题.
(7)构建方程模型,求根的个数.
(8)研究图形的形状、位置关系、性质等.
数形结合
例题
1.[成都一诊]已知函数f(x)是定义在R上的偶函数,且f(-x-1)=f(x-1),当x∈[-1,0]时,
f(x)=-x3,则关于x的方程f(x)=|cos πx|在上的所有实数解之和为________.
数形结合
50
例题
数形结合
51
例题
2.[江苏卷]已知实数则的取值范围是 .
数形结合
52
例题
解析:作出不等式组对应的平面区域,
设,则z的几何意义是区域内的点到原点距离的平方,
由图象知A到原点的距离最大,
点O到直线BC:2x+y-2=0的距离最小,
由得,即A(2,3),此时,
点O到直线BC:2x+y-2=0的距离d=
则
故z的取值范围是[,13],
答案:[,13].
数形结合
53
例题
3.[浙江卷]已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是( )
A.1 B.2 C. D.
数形结合
54
例题
数形结合
55
例题
4.[上海卷]如图,已知点O(0,0),A(1.0),B(0, 1),P是曲线上一个动点,则的取值范围是 .
数形结合
56
例题
数形结合
57
例题
5.
数形结合
58
例题
解析:不妨设
所以
上式表示点到点的距离之和为
故在线段上,
所以问题转化为求点与线段上点的距离的范围问题,
如图,易求得其范围为[].
数形结合
59
例题
6.求函数的值域.
数形结合
60
例题
数形结合
O
x
P
A
B
y
解析表示定点(2,3)到动点(cosx,sinx)的斜率,
又知动点(cosx,sinx)满足单位圆方程,
问题转化为点(2,3)到单位圆上点的连线的斜率问题.
可设出直线方程,临界条件是相切时,原点O到直线的距离等于半径1,
求出斜率即可.
答案:[ ]
61
数形结合
1.在数学中函数的图象、方程的曲线、不等式所表示的平面区域、向量的几何意义、复数的几何意义等都实现以形助数的途径,当试题中涉及这些问题的数量关系时,我们可以通过图形分析这些数量关系,达到解题的目的.
2.有些图形问题,单纯从图形上无法看出问题的结论,这就要对图形进行数量上的分析,通过数的帮助达到解题的目的.
3.利用数形结合解题,有时只需把图象大致形状画出即可,不需要精确图象.
4.数形结合思想常用模型:一次、二次函数图象;斜率公式;两点间的距离公式(或向量的模、复数的模);点到直线的距离公式等.
数形结合
高考数学冲刺(9)
函数值域技巧、数形结合技巧
主讲人: |
2
01
椭圆
焦点三角形中的秒杀结论
02
椭圆
焦点、通径、渐近线秒杀技巧
03
椭圆
中点弦模型
04
函数
奇偶性、单调性、周期性秒杀技巧
05
综合
线性规划、二项式、不等式秒杀
06
数列
列举法秒杀数列
07
数列
数列四大求和方法
08
综合
排列组合七大解题策略
09
函数
函数值域技巧、数形结合技巧
10
综合
巧解高考小题
本节说明
求函数值域的常用方法:
1.换元法 2.分离常数法 3.基本不等式法
4.导数法 5.数形结合法 6.判别式法
7. 配方法 8. 单调性法 9.观察法
3
方法1
方法2
方法3
方法4
方法5
方法6
方法7
方法8
4
1.换元法
解题步骤:
第一步:观察函数解析式的形式,函数变量较多且相互关联;
第二步:另新元代换整体,得一新函数,求出新函数的值域即为原函数的值域.
1.求函数的值域.
方法1
5
例题
2.求函数的值域.
(1)对形如的函数,可以考虑换元,消掉根号,化成一个二次函数.
(2)在任何地方换元,都要注意新元的取值范围,它就是新函数的定义域.
(3)由于,所以当已知中同时又有的和或差的形式
以及积的形式,也可以考虑换元,化成二次函数.
方法1
6
例题
第二问经过一系列的推理化简得到,,求d的取值范围.
方法1
7
例题
解析: ,
令则
,易知在(1,]上是减函数,
所以
方法1
8
练习
第二问解答时有这么一步需要求
取得最小值时的值,
我们也可以直接当成求红色部分的取值范围(值域),
方法1
9
练习
1.本题重点为求函数的值域.
方法1
10
练习
1.本题重点为求函数的值域.
解析:令则,
所以
换元后转化为二次函数求最值,计算即可.
方法1
11
2.分离常数法
解题步骤:
第一步:观察函数类型,型如;
第二步:对函数成形式;
第三步:求出函数在定义域范围内的值域,进而求函数的值域.
方法2
12
例题
1.函数,()的值域为 .
2.函数的值域为 .
方法2
13
3.基本不等式法
解题步骤:
第一步:观察函数解析式的形式,型如或的函数;
第二步:对函数进行配凑成形式,再利用基本不等式求函数的最值,
进而得到函数的值域.
方法3
例题
1.已知求函数的最小值.
2.求函数的最小值.
14
方法3
例题
1.已知求函数的最小值.
解析:因为所以
当且仅当 ,
即上式等号成立.
因为在定义域内,
所以最小值为1.
2.求函数的最小值.
解析:由题意得
+
当且仅当
即时等号成立.
所以函数最小值为
15
方法3
例题
3.(杭州模拟)已知实数若的值域为 .
方法3
例题
3.(杭州模拟)已知实数若的值域为 .
解析:
,其中,
所以
当且仅当等号成立,又当时, 取最大值,
故值域为[0,].
方法3
18
例题
4.(浙江卷)点P(0,-1)是椭圆C:的一个顶点,C的长轴是圆的直径,过点P且垂直的两条直线,其中交圆与A,B两点, 交椭圆于另一点D.
(2)求△ABD的面积取最大值时直线的方程.
第二问经过一系列的计算会得到,,求为何值时, 最大.
方法3
19
例题
解析:
当且仅当即或时等号成立.
方法3
20
练习
1.(湖北卷)已知F1,F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=,则椭圆和双曲线的离心率的倒数之和的最大值为 .
此题在第一讲中利用“交通线“秒杀结论来做的,较简单,若不用秒杀结论来做则会得到下面的式子:
假设离心率的倒数之和的平方为,则,,求其最大值.
方法3
21
练习
解析: ,
当即等号成立,
故最大值为离心率的倒数之和的最大值为.
方法3
22
练习
2.(全国II卷)设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个定点,直线与AB交于点D,与椭圆交于E,F两点.(2)求四边形AEBF面积的最大值.
第二问经过一系列的计算会得到,求其最值.
方法3
23
练习
解析,
当且仅当,即时取等号,
故四边形AEBF面积的最大值为.
方法3
24
4.数形结合法
1.求函数的值域.
2. 当,函数最小值为( )
A. 4 B. C.4 D.
方法4
25
例题
方法4
26
例题
3.对,记,函数的值域是 .
方法4
27
5.导数法
1.是抛物线C:上一点,A,B是C上的两点,线段AB被直线OM平分且P,求△ABP面积的最大.
此题在经过一系列的推理计算会得到,
,求最大值.
方法5
28
例题
解析:,
令 ,,则
令,则,
由0,所以
故△ABP面积的最大值为
方法5
求函数值域的常用方法:
1. 换元法 2. 分离常数法 3. 基本不等式法
4.导数法 5.数形结合法 6.判别式法
7. 配方法 8. 单调性法 9.观察法
当堂总结
以下内容为选讲内容,建议作为材料包
31
5.导数法
1.(浙江卷)已知P(2,1),不过原点O的直线l与椭圆C:交于A,B两点,且线段AB被直线OP平分.求△ABP的面积取最大时直线l的方程.
此题在经过一系列的推理计算会得到,
,求为值时,最大.
方法5
32
练习
解析:可以先求出面积的平方再开方来算. ,
令
求导得
,
因为,所以当时, 单调递增,
当时, 单调递减;
当= 时,△ABP的面积取得最大值.
方法5
3.不等式法
方法3
1.
在第二问中有 = ,求其范围.
34
3.不等式法
1.求函数, 的值域.
解析:令,,则
所以
又因为
所以值域为.
方法3
35
3.不等式法
2.已知椭圆C:l经过定点(0,2),且与椭圆C交于A,B两点,求△OAB面积的最大值.
经过一系列的计算会得到,,求△OAB面积的最大值.
方法3
36
练习
解析:,
当且仅当,即时等号成立,所以最大为1.
故△OAB面积的最大值为1.
方法3
3.
第二问经过一系列的计算会得到,求m的最大值可先求出最大值.
即求函数 的最大值.
37
3.不等式法
方法3
3.
第二问经过一系列的计算会得到,求m的最大值可先求出最大值.
即求函数 的最大值.
38
3.不等式法
解析:
令,则,
所以
当即时,取得最大值.
方法3
39
6.判别式法
解题步骤:
第一步:观察函数解析式的形式,型如的函数;
第二步:将函数式化成关于x的方程,且方程有解,用根的判别式求出参数y的取值范围,
即得函数的值域.
方法6
40
例题
1.求函数的值域.
2.求函数的值域.
方法6
41
例题
1.求函数的值域.
解析:因为2>0,所以函数的定义域为R.
原函数转化为
整理得
当时,上式可以看成关于的二次方程,时此方程有实数根,
即.
当时,方程为7=0,显然不成立,故,经检验时有解.
所以
方法6
42
7.配方法
1.(重庆)函数的最小值为 .
2.函数的值域为 .
方法7
43
例题
方法7
44
例题
方法7
45
8.单调性法
1.求函数的值域.
2.求函数的值域.
3.求函数的值域.
方法8
46
例题
4.求函数+的值域.
5.求函数的值域.
6.已知,则的最大值.
方法8
数形结合
1.数形结合的数学思想:包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:
一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,
比如应用函数的图象来直观地说明函数的性质;
二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,
如应用曲线的方程来精确地阐明曲线的几何性质.
数形结合
48
数形结合
2.数形结合思想解决的问题常有以下几种:
(1)构建函数模型并结合其图象求参数的取值范围.
(2)构建函数模型并结合其图象研究方程根的范围.
(3)构建函数模型并结合其图象研究量与量之间的大小关系.
(4)构建函数模型并结合其几何意义研究函数的最值问题和证明不等式.
(5)构建立体几何模型研究代数问题.
(6)构建解析几何中的斜率、截距、距离等模型研究最值问题.
(7)构建方程模型,求根的个数.
(8)研究图形的形状、位置关系、性质等.
数形结合
例题
1.[成都一诊]已知函数f(x)是定义在R上的偶函数,且f(-x-1)=f(x-1),当x∈[-1,0]时,
f(x)=-x3,则关于x的方程f(x)=|cos πx|在上的所有实数解之和为________.
数形结合
50
例题
数形结合
51
例题
2.[江苏卷]已知实数则的取值范围是 .
数形结合
52
例题
解析:作出不等式组对应的平面区域,
设,则z的几何意义是区域内的点到原点距离的平方,
由图象知A到原点的距离最大,
点O到直线BC:2x+y-2=0的距离最小,
由得,即A(2,3),此时,
点O到直线BC:2x+y-2=0的距离d=
则
故z的取值范围是[,13],
答案:[,13].
数形结合
53
例题
3.[浙江卷]已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是( )
A.1 B.2 C. D.
数形结合
54
例题
数形结合
55
例题
4.[上海卷]如图,已知点O(0,0),A(1.0),B(0, 1),P是曲线上一个动点,则的取值范围是 .
数形结合
56
例题
数形结合
57
例题
5.
数形结合
58
例题
解析:不妨设
所以
上式表示点到点的距离之和为
故在线段上,
所以问题转化为求点与线段上点的距离的范围问题,
如图,易求得其范围为[].
数形结合
59
例题
6.求函数的值域.
数形结合
60
例题
数形结合
O
x
P
A
B
y
解析表示定点(2,3)到动点(cosx,sinx)的斜率,
又知动点(cosx,sinx)满足单位圆方程,
问题转化为点(2,3)到单位圆上点的连线的斜率问题.
可设出直线方程,临界条件是相切时,原点O到直线的距离等于半径1,
求出斜率即可.
答案:[ ]
61
数形结合
1.在数学中函数的图象、方程的曲线、不等式所表示的平面区域、向量的几何意义、复数的几何意义等都实现以形助数的途径,当试题中涉及这些问题的数量关系时,我们可以通过图形分析这些数量关系,达到解题的目的.
2.有些图形问题,单纯从图形上无法看出问题的结论,这就要对图形进行数量上的分析,通过数的帮助达到解题的目的.
3.利用数形结合解题,有时只需把图象大致形状画出即可,不需要精确图象.
4.数形结合思想常用模型:一次、二次函数图象;斜率公式;两点间的距离公式(或向量的模、复数的模);点到直线的距离公式等.
数形结合
同课章节目录
