6.4.2向量在物理中的应用举例课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(11张ppt)
文档属性
| 名称 | 6.4.2向量在物理中的应用举例课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(11张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 17:12:36 | ||
图片预览




文档简介
(共11张PPT)
人教2019A版必修 第二册
6.4.2 向量在物理中的应用举例
第六章 平面向量及其应用
两个人一起提一个重物时,怎样提它更省力?
人用双手支撑立在双杠上,所用力的大小与双杠的宽度存在怎样的关系?
夹角越大越费力
数学解释?
情景引入
本节课我们主要来学习向量在物理中应用
例1. 在日常生活中,我们有这样的经验:两个人共提一个旅行包,两个拉力夹角越大越费力;在单杠上做引体向上运动,两臂的夹角越小越省力. 你能从数学的角度解释这种形象吗?
分析: 不妨以两人共提旅行包为例,只要研究清楚两个拉力的合力、 旅行包所受的重 力以及两个拉力的夹角三者之间的关系,就可以获得问题的数学解释.
为研究方便,不妨设,大小相等。
新课讲解
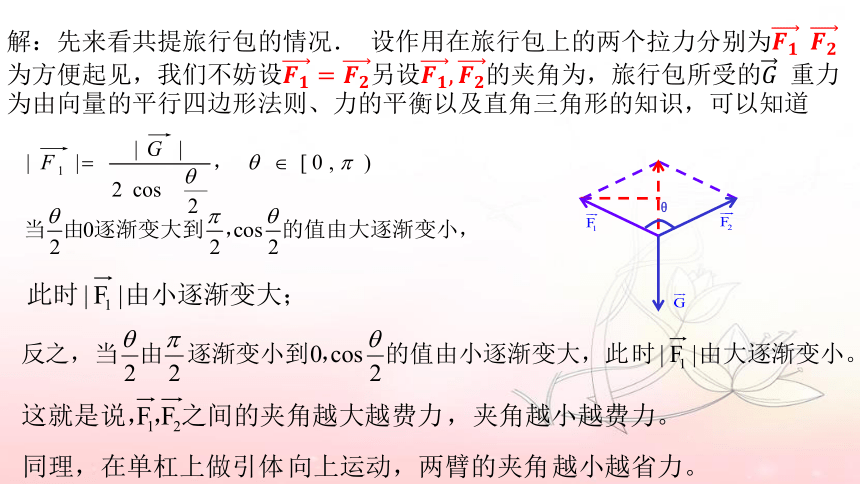
解:先来看共提旅行包的情况. 设作用在旅行包上的两个拉力分别为为方便起见,我们不妨设另设的夹角为,旅行包所受的 重力为由向量的平行四边形法则、力的平衡以及直角三角形的知识,可以知道
θ
(1)要使 最小,只需 最大,此时 即 。
的最小值为
(2)要使 ,
只需
即
分析:如果水是静止的,那么船只要取垂直于河岸的方向行驶,就能使航程最短,此时所用时间也是最短的.考虑到水的流速,要使航程最短,船的速度与水流速度的合速度v必须垂直于河岸.
例2:如图,一条河的两岸平行,河的宽度d=500m,一艘船从河岸边的A地出发,向河对岸航行,已知船的速度V1的大小为|v1|=10㎞/h,水流速度V2的大小为|v2|= 2㎞/h,那么当航程最短时,这艘船行驶完全程需要多长时间(精准到0.1min)?
解:设点B是河对岸一点,AB与河岸垂直,那么当这艘船实际沿着AB方向行驶时,船的航程最短。
如图,设
此时,船的航行时间
所以,当航程最短时,这艘船行驶完全程需要3.1min。
则
(1)问题的转化:把物理问题转化为数学问题;
(2)模型的建立:建立以向量为主体的数学模型;
(3)参数的获得:求出数学模型的有关解——理论参数值;
(4)问题的答案:回到问题的初始状态,解决相关物理现象.
思考:你能总结用向量解决物理问题的一般步骤吗
随堂练习
小结
人教2019A版必修 第二册
6.4.2 向量在物理中的应用举例
第六章 平面向量及其应用
两个人一起提一个重物时,怎样提它更省力?
人用双手支撑立在双杠上,所用力的大小与双杠的宽度存在怎样的关系?
夹角越大越费力
数学解释?
情景引入
本节课我们主要来学习向量在物理中应用
例1. 在日常生活中,我们有这样的经验:两个人共提一个旅行包,两个拉力夹角越大越费力;在单杠上做引体向上运动,两臂的夹角越小越省力. 你能从数学的角度解释这种形象吗?
分析: 不妨以两人共提旅行包为例,只要研究清楚两个拉力的合力、 旅行包所受的重 力以及两个拉力的夹角三者之间的关系,就可以获得问题的数学解释.
为研究方便,不妨设,大小相等。
新课讲解
解:先来看共提旅行包的情况. 设作用在旅行包上的两个拉力分别为为方便起见,我们不妨设另设的夹角为,旅行包所受的 重力为由向量的平行四边形法则、力的平衡以及直角三角形的知识,可以知道
θ
(1)要使 最小,只需 最大,此时 即 。
的最小值为
(2)要使 ,
只需
即
分析:如果水是静止的,那么船只要取垂直于河岸的方向行驶,就能使航程最短,此时所用时间也是最短的.考虑到水的流速,要使航程最短,船的速度与水流速度的合速度v必须垂直于河岸.
例2:如图,一条河的两岸平行,河的宽度d=500m,一艘船从河岸边的A地出发,向河对岸航行,已知船的速度V1的大小为|v1|=10㎞/h,水流速度V2的大小为|v2|= 2㎞/h,那么当航程最短时,这艘船行驶完全程需要多长时间(精准到0.1min)?
解:设点B是河对岸一点,AB与河岸垂直,那么当这艘船实际沿着AB方向行驶时,船的航程最短。
如图,设
此时,船的航行时间
所以,当航程最短时,这艘船行驶完全程需要3.1min。
则
(1)问题的转化:把物理问题转化为数学问题;
(2)模型的建立:建立以向量为主体的数学模型;
(3)参数的获得:求出数学模型的有关解——理论参数值;
(4)问题的答案:回到问题的初始状态,解决相关物理现象.
思考:你能总结用向量解决物理问题的一般步骤吗
随堂练习
小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
