沪科版 数学八年级上册 12.1函数(第3课时)教案(表格式)
文档属性
| 名称 | 沪科版 数学八年级上册 12.1函数(第3课时)教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 94.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览

文档简介
项目 内容
课题 12.1函数 (第 3 课时)
教学目标 (一) 知识与技能? 1.知道函数图象的意义; 2.能画出简单函数的图象,会列表、描点、连线; 3.会根据情境选择正确的图象。 (二)过程与方法 通过列表、描点、连线,体验数形结合这种重要的思想方法。 (三)情感目标? 1.通过实例探究,培养学生深入探究的学习精神; 2.使学生对所学知识进行融会贯通,深化对数形结合思想的理解。
教学重、 难点 重点:函数的图象法,让学生发现坐标系中纵、横轴所表示的两个量之间的联系就是函数关系 难点:让学生感受到用光滑曲线依次把所描的点连起来组成函数图象的合理性
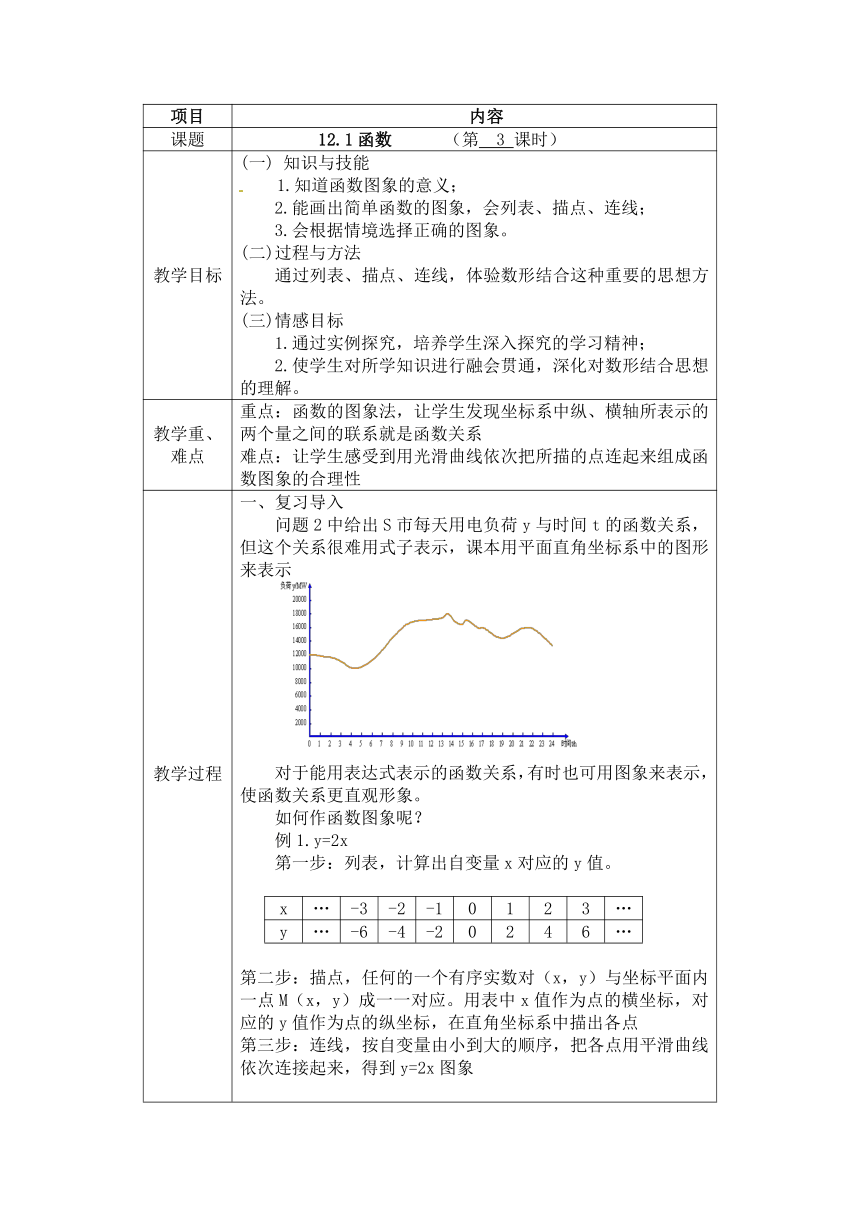
教学过程 一、复习导入 问题2中给出S市每天用电负荷y与时间t的函数关系,但这个关系很难用式子表示,课本用平面直角坐标系中的图形来表示 对于能用表达式表示的函数关系,有时也可用图象来表示,使函数关系更直观形象。 如何作函数图象呢? 例1.y=2x 第一步:列表,计算出自变量x对应的y值。 x…-3-2-10123…y…-6-4-20246…
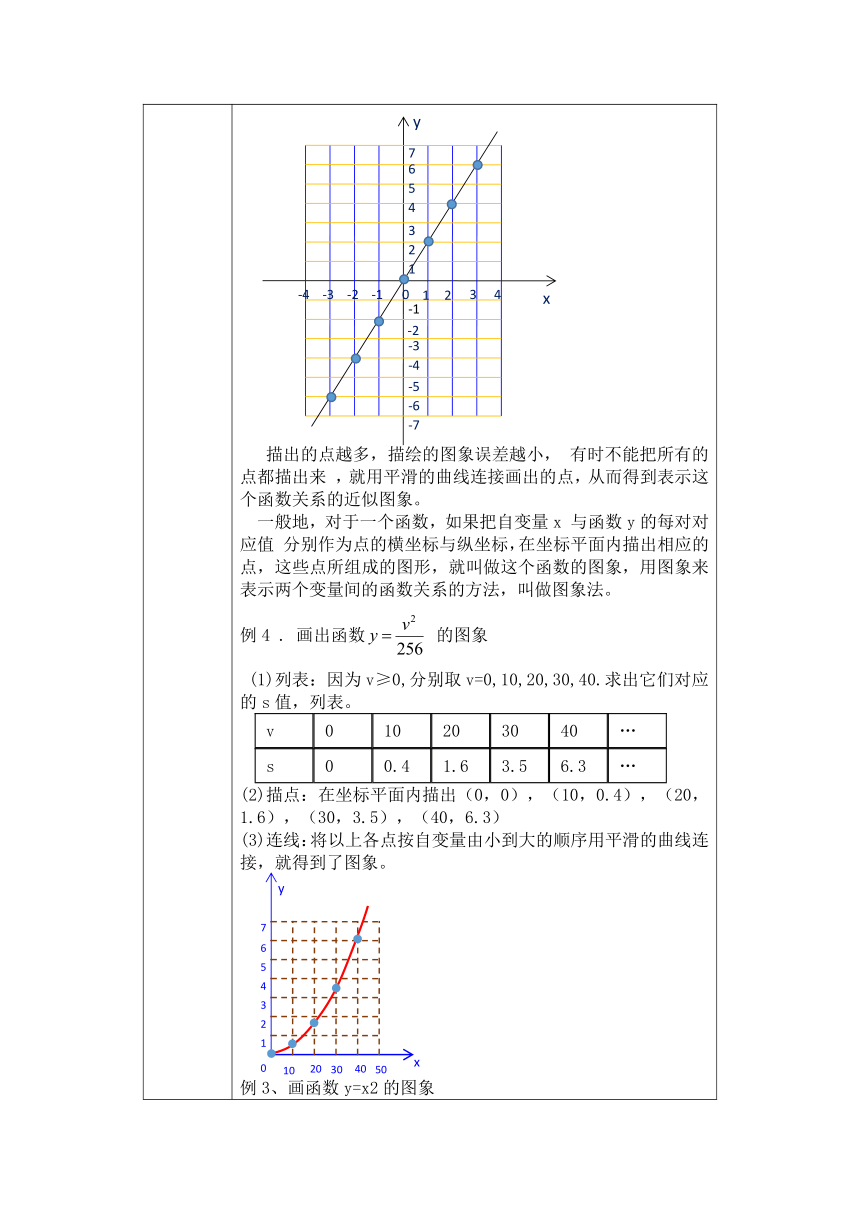
第二步:描点,任何的一个有序实数对(x,y)与坐标平面内一点M(x,y)成一一对应。用表中x值作为点的横坐标,对应的y值作为点的纵坐标,在直角坐标系中描出各点 第三步:连线,按自变量由小到大的顺序,把各点用平滑曲线依次连接起来,得到y=2x图象 描出的点越多,描绘的图象误差越小, 有时不能把所有的点都描出来 ,就用平滑的曲线连接画出的点,从而得到表示这个函数关系的近似图象。 一般地,对于一个函数,如果把自变量x 与函数y的每对对应值 分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就叫做这个函数的图象,用图象来表示两个变量间的函数关系的方法,叫做图象法。 例4 . 画出函数 的图象 (1)列表:因为v≥0,分别取v=0,10,20,30,40.求出它们对应的s值,列表。 v010203040…s00.41.63.56.3…
描点:在坐标平面内描出(0,0),(10,0.4),(20,1.6),(30,3.5),(40,6.3) 连线:将以上各点按自变量由小到大的顺序用平滑的曲线连接,就得到了图象。 例3、画函数y=x2的图象 列表: x…-2-1012…y…41014…
描点:用表中对应的x 、y的值作为点的横坐标和纵坐标在平面内描出各点。 连线:按自变量由小到大的顺序用平滑的曲线连接各点,并向上延伸。 练习、画出函数y=x+0.5的图象 1、列表 x-3-2-10123y-2.5-1.5-0.50.51.52.53.5
描点 画线 四、课堂小结: 函数关系的三种表示方法 1.列表法——通过列出自变量的值与对应函数值的表格来表示函数关系的方法 2.解析法——用数学式子表示函数关系的方法.其中的等式叫做解析式 3.图象法——般地,对于一个函数,把自变量x与函数y的每对对应值分别做为点的横、纵坐标,在坐标平面内描出相应的点,由这些点组成的图形,就叫做这个函数的图象 这三种表示函数的方法各有优缺点。 1、用解析法表示函数关系: 优点:简单明了。能从解析式清楚看到两个变量之间的全部相依关系,并且适合进行理论分析和推导计算。 缺点:在求对应值时,有时要做较复杂的计算。 2、用列表表示函数关系 优点:对于表中自变量的每一个值,可以不通过计算,直接把函数值找到,查询时很方便。 缺点:表中不能把所有的自变量与函数对应值全部列出,而且从表中看不出变量间的对应规律。 3、用图象法表示函数关系 优点:形象直观,可以形象地反映出函数关系变化的趋势和某些性质,把抽象的函数概念形象化。 缺点:从自变量的值常常难以找到对应的函数的准确值。 函数的三种基本表示方法,各有各的优点和缺点,因此,要根据不同问题与需要,灵活地采用不同的方法。在数学或其他科学研究与应用上,有时把这三种方法结合起来使用,即由已知的函数解析式,列出自变量与对应的函数值的表格,再画出它的图象。 布置作业: 同步练习 p18
课题 12.1函数 (第 3 课时)
教学目标 (一) 知识与技能? 1.知道函数图象的意义; 2.能画出简单函数的图象,会列表、描点、连线; 3.会根据情境选择正确的图象。 (二)过程与方法 通过列表、描点、连线,体验数形结合这种重要的思想方法。 (三)情感目标? 1.通过实例探究,培养学生深入探究的学习精神; 2.使学生对所学知识进行融会贯通,深化对数形结合思想的理解。
教学重、 难点 重点:函数的图象法,让学生发现坐标系中纵、横轴所表示的两个量之间的联系就是函数关系 难点:让学生感受到用光滑曲线依次把所描的点连起来组成函数图象的合理性
教学过程 一、复习导入 问题2中给出S市每天用电负荷y与时间t的函数关系,但这个关系很难用式子表示,课本用平面直角坐标系中的图形来表示 对于能用表达式表示的函数关系,有时也可用图象来表示,使函数关系更直观形象。 如何作函数图象呢? 例1.y=2x 第一步:列表,计算出自变量x对应的y值。 x…-3-2-10123…y…-6-4-20246…
第二步:描点,任何的一个有序实数对(x,y)与坐标平面内一点M(x,y)成一一对应。用表中x值作为点的横坐标,对应的y值作为点的纵坐标,在直角坐标系中描出各点 第三步:连线,按自变量由小到大的顺序,把各点用平滑曲线依次连接起来,得到y=2x图象 描出的点越多,描绘的图象误差越小, 有时不能把所有的点都描出来 ,就用平滑的曲线连接画出的点,从而得到表示这个函数关系的近似图象。 一般地,对于一个函数,如果把自变量x 与函数y的每对对应值 分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就叫做这个函数的图象,用图象来表示两个变量间的函数关系的方法,叫做图象法。 例4 . 画出函数 的图象 (1)列表:因为v≥0,分别取v=0,10,20,30,40.求出它们对应的s值,列表。 v010203040…s00.41.63.56.3…
描点:在坐标平面内描出(0,0),(10,0.4),(20,1.6),(30,3.5),(40,6.3) 连线:将以上各点按自变量由小到大的顺序用平滑的曲线连接,就得到了图象。 例3、画函数y=x2的图象 列表: x…-2-1012…y…41014…
描点:用表中对应的x 、y的值作为点的横坐标和纵坐标在平面内描出各点。 连线:按自变量由小到大的顺序用平滑的曲线连接各点,并向上延伸。 练习、画出函数y=x+0.5的图象 1、列表 x-3-2-10123y-2.5-1.5-0.50.51.52.53.5
描点 画线 四、课堂小结: 函数关系的三种表示方法 1.列表法——通过列出自变量的值与对应函数值的表格来表示函数关系的方法 2.解析法——用数学式子表示函数关系的方法.其中的等式叫做解析式 3.图象法——般地,对于一个函数,把自变量x与函数y的每对对应值分别做为点的横、纵坐标,在坐标平面内描出相应的点,由这些点组成的图形,就叫做这个函数的图象 这三种表示函数的方法各有优缺点。 1、用解析法表示函数关系: 优点:简单明了。能从解析式清楚看到两个变量之间的全部相依关系,并且适合进行理论分析和推导计算。 缺点:在求对应值时,有时要做较复杂的计算。 2、用列表表示函数关系 优点:对于表中自变量的每一个值,可以不通过计算,直接把函数值找到,查询时很方便。 缺点:表中不能把所有的自变量与函数对应值全部列出,而且从表中看不出变量间的对应规律。 3、用图象法表示函数关系 优点:形象直观,可以形象地反映出函数关系变化的趋势和某些性质,把抽象的函数概念形象化。 缺点:从自变量的值常常难以找到对应的函数的准确值。 函数的三种基本表示方法,各有各的优点和缺点,因此,要根据不同问题与需要,灵活地采用不同的方法。在数学或其他科学研究与应用上,有时把这三种方法结合起来使用,即由已知的函数解析式,列出自变量与对应的函数值的表格,再画出它的图象。 布置作业: 同步练习 p18
