湖南省永州市零陵区2021-2022学年八年级上学期期末数学试卷(Word版无答案)
文档属性
| 名称 | 湖南省永州市零陵区2021-2022学年八年级上学期期末数学试卷(Word版无答案) | 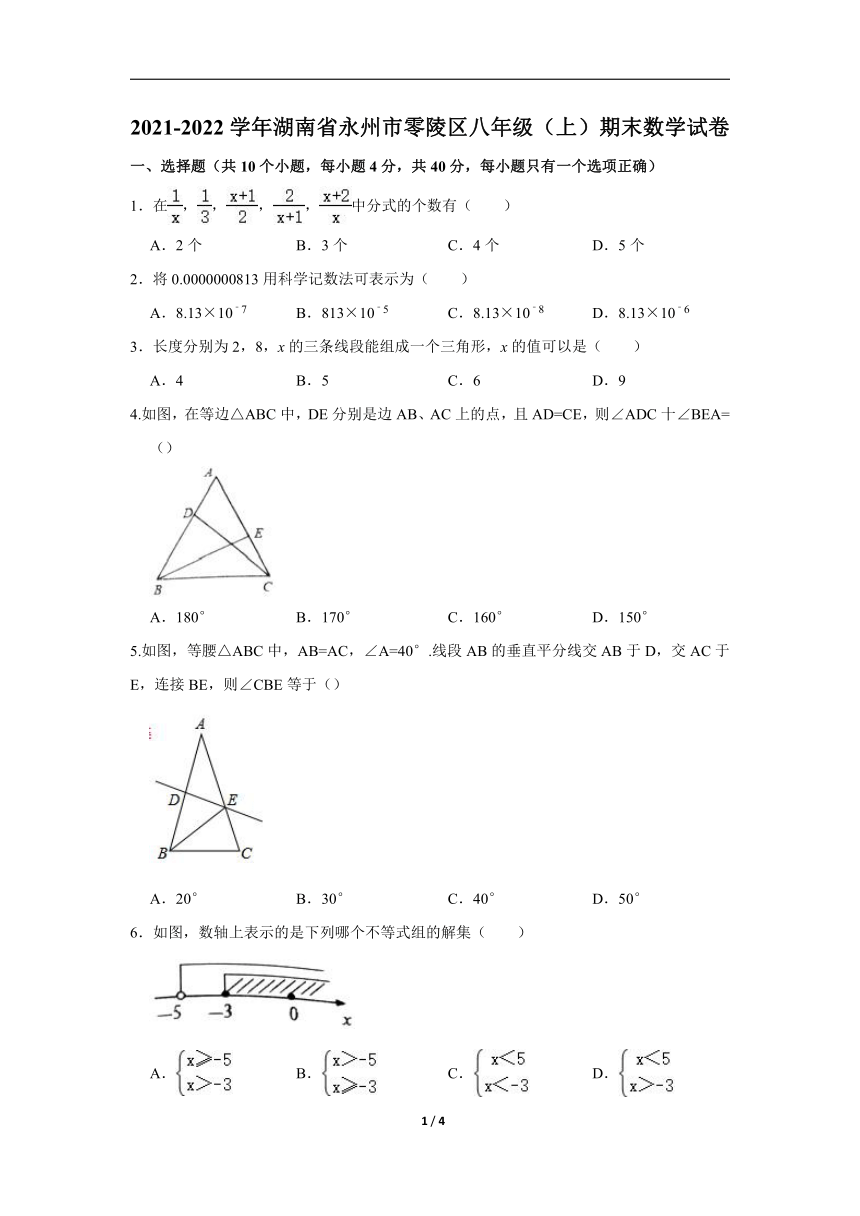 | |
| 格式 | doc | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 17:55:38 | ||
图片预览


文档简介
2021-2022学年湖南省永州市零陵区八年级(上)期末数学试卷
一、选择题(共10个小题,每小题4分,共40分,每小题只有一个选项正确)
1.在,,,,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.将0.0000000813用科学记数法可表示为( )
A.8.13×10﹣7 B.813×10﹣5 C.8.13×10﹣8 D.8.13×10﹣6
3.长度分别为2,8,x的三条线段能组成一个三角形,x的值可以是( )
A.4 B.5 C.6 D.9
4.如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC十∠BEA=()
A.180° B.170° C.160° D.150°
5.如图,等腰△ABC中,AB=AC,∠A=40°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()
A.20° B.30° C.40° D.50°
6.如图,数轴上表示的是下列哪个不等式组的解集( )
A. B. C. D.
7.关于x的分式方程=2的解为正数,则m的取值范围是( )
A.m>﹣1 B.m≠1 C.m>1且m≠﹣1 D.m>﹣1且m≠1
8.下列各结论中,正确的是( )
A. B.
C.=±16 D.
9.货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是()A. B. C. D.
10.某班数学兴趣小组对不等式组,讨论得到以下结论:
①若a=6,则不等式组的解集为3<x≤6;
②若a=3,则不等式组无解;
③若不等式组有解,则a的取值范围a≥3;
④若不等式组只有四个整数解,则a的值只可以为7.
其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8个小题,每小题4分,共32分)
11.计算(﹣)﹣2+(﹣π)0= .
12.命题“等腰三角形的两个底角相等”的逆命题是 .
13.若解分式方程=产生增根,则增根可能是 .
I4.如图,已知AB、CD相交于点P,AP=BP,请增加一个条件,使△ADP≌△BCP(不能添加辅助线),你增加的条件是
15.已知一个正数的平方根是3x+2和5x+14,则这个数是 .
16.分式方程的解为 .
17.若关于x的不等式组的解集为3≤x≤4,则关于x的不等式ax+b<0的解集为 .
18.某校数学课外小组利用数轴为学校门口的一条马路设计植树方案如下:第k棵树种植在点xk处,其中x1=1,当k≥2时,,T(a)表示非负实数a的整数部分, 例如T(2.6)=2,T(0.2)=0.按此方案,第6棵树种植点x6为 ;第2021棵树种植点x2021为 .
三、解答题(共8小题,满分78分)
19.计算:
(1);
(2).
20.解不等式组:,并把解集在数轴上表示出来.
21.先化简,再求值:,其中x=+1
22.已知a,b为实数,且满足关系式:|a﹣2b|+(3a﹣b﹣10)2=0.
求:(1)a,b的值;
(2)的平方根.
23.如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=20,EC=8,求BC的长.
24.已知三角形三边之长能求出三角形的面积吗?
我国宋代数学家秦九韶提出的“三斜求积术”,告诉你计算的方法是:S=,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长之半,即p=请你利用公式解答下列问题.
(I)在△ABC中,已知AB=4,BC=6,CA=8,求△ABC的面积;
(2)计算(1)中△ABC的BC边上的高.
25.为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品,已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(I)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?
26.(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD十CE是否成立?如成立,请你给出证明;若不成立,请说明理由,
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
2 / 2
一、选择题(共10个小题,每小题4分,共40分,每小题只有一个选项正确)
1.在,,,,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.将0.0000000813用科学记数法可表示为( )
A.8.13×10﹣7 B.813×10﹣5 C.8.13×10﹣8 D.8.13×10﹣6
3.长度分别为2,8,x的三条线段能组成一个三角形,x的值可以是( )
A.4 B.5 C.6 D.9
4.如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC十∠BEA=()
A.180° B.170° C.160° D.150°
5.如图,等腰△ABC中,AB=AC,∠A=40°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()
A.20° B.30° C.40° D.50°
6.如图,数轴上表示的是下列哪个不等式组的解集( )
A. B. C. D.
7.关于x的分式方程=2的解为正数,则m的取值范围是( )
A.m>﹣1 B.m≠1 C.m>1且m≠﹣1 D.m>﹣1且m≠1
8.下列各结论中,正确的是( )
A. B.
C.=±16 D.
9.货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是()A. B. C. D.
10.某班数学兴趣小组对不等式组,讨论得到以下结论:
①若a=6,则不等式组的解集为3<x≤6;
②若a=3,则不等式组无解;
③若不等式组有解,则a的取值范围a≥3;
④若不等式组只有四个整数解,则a的值只可以为7.
其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8个小题,每小题4分,共32分)
11.计算(﹣)﹣2+(﹣π)0= .
12.命题“等腰三角形的两个底角相等”的逆命题是 .
13.若解分式方程=产生增根,则增根可能是 .
I4.如图,已知AB、CD相交于点P,AP=BP,请增加一个条件,使△ADP≌△BCP(不能添加辅助线),你增加的条件是
15.已知一个正数的平方根是3x+2和5x+14,则这个数是 .
16.分式方程的解为 .
17.若关于x的不等式组的解集为3≤x≤4,则关于x的不等式ax+b<0的解集为 .
18.某校数学课外小组利用数轴为学校门口的一条马路设计植树方案如下:第k棵树种植在点xk处,其中x1=1,当k≥2时,,T(a)表示非负实数a的整数部分, 例如T(2.6)=2,T(0.2)=0.按此方案,第6棵树种植点x6为 ;第2021棵树种植点x2021为 .
三、解答题(共8小题,满分78分)
19.计算:
(1);
(2).
20.解不等式组:,并把解集在数轴上表示出来.
21.先化简,再求值:,其中x=+1
22.已知a,b为实数,且满足关系式:|a﹣2b|+(3a﹣b﹣10)2=0.
求:(1)a,b的值;
(2)的平方根.
23.如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=20,EC=8,求BC的长.
24.已知三角形三边之长能求出三角形的面积吗?
我国宋代数学家秦九韶提出的“三斜求积术”,告诉你计算的方法是:S=,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长之半,即p=请你利用公式解答下列问题.
(I)在△ABC中,已知AB=4,BC=6,CA=8,求△ABC的面积;
(2)计算(1)中△ABC的BC边上的高.
25.为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品,已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(I)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?
26.(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD十CE是否成立?如成立,请你给出证明;若不成立,请说明理由,
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
2 / 2
同课章节目录
