湖南省株洲市天元区2021-2022学年九年级上学期期末考试数学试题(Word版无答案)
文档属性
| 名称 | 湖南省株洲市天元区2021-2022学年九年级上学期期末考试数学试题(Word版无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览


文档简介
2021-2022学年湖南省株洲市天元区九年级(上)期末数学试卷
一.选择题(共10小题,满分40分,每小题4分)
1.﹣2021的相反数等于( )
A.2021 B.﹣2021 C. D.﹣
2.已知实数x,y满足方程组,则4x﹣y的值为( )
A.﹣1 B.1 C.﹣3 D.3
3.下列计算正确的是( )
A.(m﹣n)2=m2﹣n2 B.(2ab3)2=2a2b6
C.2xy+3xy=5xy D.a2 a4=a8
4.如图, ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是()
A.EH=HG
B.四边形EFGH是平行四边形
C.AC⊥BD
D.△ABO的面积是△EFO的面积的2倍
5,小明收集了株洲市某酒店2021年3月1日~3月6日每天的用水量(单位:吨),整理并绘制成如图所示的折线统计图,下列结论正确的是()
A.平均数是 B.众数是10
C.中位数是5.5 D.极差是
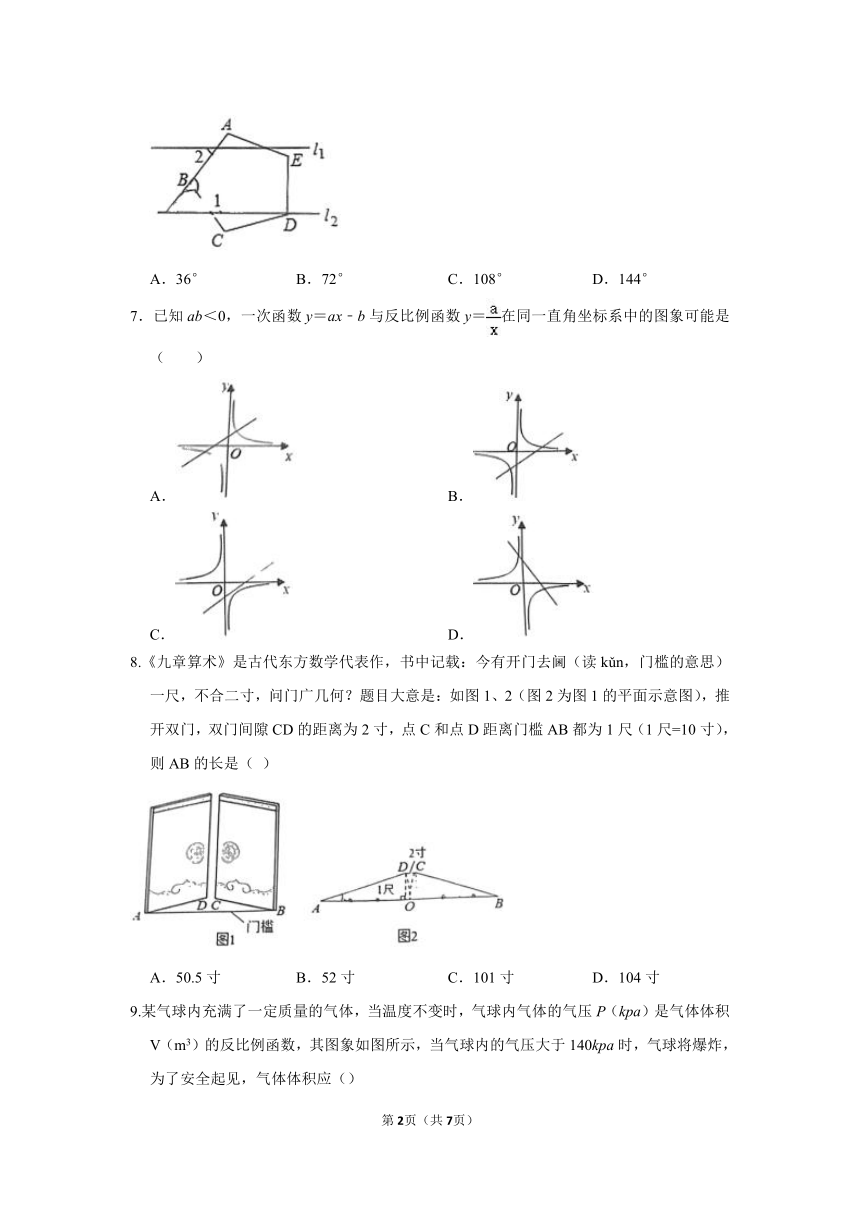
6.如图,五边形ABCDE是正五边形,若l1∥l2,则∠1﹣∠2的值是( )
A.36° B.72° C.108° D.144°
7.已知ab<0,一次函数y=ax﹣b与反比例函数y=在同一直角坐标系中的图象可能是( )
A. B.
C. D.
8.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将爆炸,为了安全起见,气体体积应()
A.不大于m3 B.不小于m3
C.不大于m3 D.不小于m3
10.如图所示是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①①a﹣b+c>0;②3a+c>0 ③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n+1没有实数根.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分32分,每小题4分)
11.比较大小: (填写“>”或“<”或“=”).
12.把多项式8a3﹣2a分解因式的结果是 .
13.2021年株洲市成功举办了“中国国际轨道交通博览会”,轨博会成果满满,70个项目总投资1216.3亿元,将1216.3亿元用科学记数法表示为 亿元.
14.把抛物线y=2x2+1向下平移1个单位长度,得到的抛物线的解析式为 .
15.已知点P(1﹣a,2a+6)在第四象限,则a的取值范围是 .
16.如图,△ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△OAC,则PQ的长等于 .
17.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,),称为点P的“倒影点”,直线y=﹣x+1上有两y点A、B它们的倒影点A′、B′均在反比例函数y=的图象上,若AB=2,则k= .
18.如图.已知∠MON是一个锐角,以点O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再分别以点A、B为圆心,大于AB长为半径画弧,两弧交于点C,画射线OC.过点A作AD∥ON,交射线OC于点D,过点D作DE⊥OC,交ON于点E.设OA=10,DE=12,则sin∠MON=
三、解答题(本大题8小题,共78分)
19.计算:()﹣1﹣(2021+π)0+4sin60°﹣.
20.先化简,再求值:÷(1﹣),其中x=+1
21.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
22.一辆自行车竖直摆放在水平地面上如图所示,右边是它的示意图,横梁AC平行于水平面MN,现测得BC=80cm.∠CAB=60°,∠ACB=50°,B到MN的距离BE=30cm,AD为可调节高度,经研究发现,当坐垫高度为身高的0.6倍时,骑行者最舒适,现一身高170cm的同学骑车,当AD长约为多少时,可以使骑行者最舒适?(结果保留一位小数,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,=1.73)
23.为落实湖南省共青团“青年大学习”的号召,株洲市天元区某中学团委针对该校学生每周参加“青年大学习”的时间(单位:)进行了随机抽样调查,并将获得的数据绘制成如下统计表和如图所示的统计图,请根据图表中的信息回答下列问题.
周学习时间 频数 频率
0≤t<1 5 0.05
1≤t<2 20 0.20
2≤t<3 a 0.35
3≤t<4 25 m
4≤t≤5 15 0.15
(1)求统计表中a,m的值.
(2)甲同学说“我的周学习时间是此次抽样调查所得数据的中位数”,求甲同学的周学习时间范围.
(3)已知该校学生约有3000人,试估计该校学生每周参加“青年大学习”的时间不少于3h的人数.
24.已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0,
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且x12+x22﹣x1x2=13,求m的值.
25.如图,已知直线y=2x十2与x轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数y=图像上,过点B作BF⊥OC,垂足为F,设OF=t.
(1)求∠ACO的正切值;
(2)求点B的坐标(用含t的式子表示);
(3)已知直线y=2x+2与反比例函数y=图像都经过第一象限的点D,连结DE,如果DE⊥x轴,求m的值.
26.如图,在直角坐标系中有Rt△AOB,O为坐标原点,OB=1,tan∠ABO=3,将此三角形绕原点O顺时针旋转90°,得到Rt△COD,二次函数y=﹣x2+bx+c的图象刚好经过A,B,C三点.
(1)求二次函数的解析式及顶点P的坐标;
(2)过定点Q(1,3)的直线l:y=kx﹣k+3与二次函数的图象相交于M,N两点.
①若S△PMN=2,求k的值;
②证明:无论k为何值,△PMN恒为直角三角形.
第1页(共1页)
一.选择题(共10小题,满分40分,每小题4分)
1.﹣2021的相反数等于( )
A.2021 B.﹣2021 C. D.﹣
2.已知实数x,y满足方程组,则4x﹣y的值为( )
A.﹣1 B.1 C.﹣3 D.3
3.下列计算正确的是( )
A.(m﹣n)2=m2﹣n2 B.(2ab3)2=2a2b6
C.2xy+3xy=5xy D.a2 a4=a8
4.如图, ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是()
A.EH=HG
B.四边形EFGH是平行四边形
C.AC⊥BD
D.△ABO的面积是△EFO的面积的2倍
5,小明收集了株洲市某酒店2021年3月1日~3月6日每天的用水量(单位:吨),整理并绘制成如图所示的折线统计图,下列结论正确的是()
A.平均数是 B.众数是10
C.中位数是5.5 D.极差是
6.如图,五边形ABCDE是正五边形,若l1∥l2,则∠1﹣∠2的值是( )
A.36° B.72° C.108° D.144°
7.已知ab<0,一次函数y=ax﹣b与反比例函数y=在同一直角坐标系中的图象可能是( )
A. B.
C. D.
8.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将爆炸,为了安全起见,气体体积应()
A.不大于m3 B.不小于m3
C.不大于m3 D.不小于m3
10.如图所示是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①①a﹣b+c>0;②3a+c>0 ③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n+1没有实数根.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分32分,每小题4分)
11.比较大小: (填写“>”或“<”或“=”).
12.把多项式8a3﹣2a分解因式的结果是 .
13.2021年株洲市成功举办了“中国国际轨道交通博览会”,轨博会成果满满,70个项目总投资1216.3亿元,将1216.3亿元用科学记数法表示为 亿元.
14.把抛物线y=2x2+1向下平移1个单位长度,得到的抛物线的解析式为 .
15.已知点P(1﹣a,2a+6)在第四象限,则a的取值范围是 .
16.如图,△ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△OAC,则PQ的长等于 .
17.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,),称为点P的“倒影点”,直线y=﹣x+1上有两y点A、B它们的倒影点A′、B′均在反比例函数y=的图象上,若AB=2,则k= .
18.如图.已知∠MON是一个锐角,以点O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再分别以点A、B为圆心,大于AB长为半径画弧,两弧交于点C,画射线OC.过点A作AD∥ON,交射线OC于点D,过点D作DE⊥OC,交ON于点E.设OA=10,DE=12,则sin∠MON=
三、解答题(本大题8小题,共78分)
19.计算:()﹣1﹣(2021+π)0+4sin60°﹣.
20.先化简,再求值:÷(1﹣),其中x=+1
21.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
22.一辆自行车竖直摆放在水平地面上如图所示,右边是它的示意图,横梁AC平行于水平面MN,现测得BC=80cm.∠CAB=60°,∠ACB=50°,B到MN的距离BE=30cm,AD为可调节高度,经研究发现,当坐垫高度为身高的0.6倍时,骑行者最舒适,现一身高170cm的同学骑车,当AD长约为多少时,可以使骑行者最舒适?(结果保留一位小数,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,=1.73)
23.为落实湖南省共青团“青年大学习”的号召,株洲市天元区某中学团委针对该校学生每周参加“青年大学习”的时间(单位:)进行了随机抽样调查,并将获得的数据绘制成如下统计表和如图所示的统计图,请根据图表中的信息回答下列问题.
周学习时间 频数 频率
0≤t<1 5 0.05
1≤t<2 20 0.20
2≤t<3 a 0.35
3≤t<4 25 m
4≤t≤5 15 0.15
(1)求统计表中a,m的值.
(2)甲同学说“我的周学习时间是此次抽样调查所得数据的中位数”,求甲同学的周学习时间范围.
(3)已知该校学生约有3000人,试估计该校学生每周参加“青年大学习”的时间不少于3h的人数.
24.已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0,
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且x12+x22﹣x1x2=13,求m的值.
25.如图,已知直线y=2x十2与x轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数y=图像上,过点B作BF⊥OC,垂足为F,设OF=t.
(1)求∠ACO的正切值;
(2)求点B的坐标(用含t的式子表示);
(3)已知直线y=2x+2与反比例函数y=图像都经过第一象限的点D,连结DE,如果DE⊥x轴,求m的值.
26.如图,在直角坐标系中有Rt△AOB,O为坐标原点,OB=1,tan∠ABO=3,将此三角形绕原点O顺时针旋转90°,得到Rt△COD,二次函数y=﹣x2+bx+c的图象刚好经过A,B,C三点.
(1)求二次函数的解析式及顶点P的坐标;
(2)过定点Q(1,3)的直线l:y=kx﹣k+3与二次函数的图象相交于M,N两点.
①若S△PMN=2,求k的值;
②证明:无论k为何值,△PMN恒为直角三角形.
第1页(共1页)
同课章节目录
