2021-2022学年沪科版九年级下册数学第24圆单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级下册数学第24圆单元测试卷(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 356.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 16:22:35 | ||
图片预览

文档简介
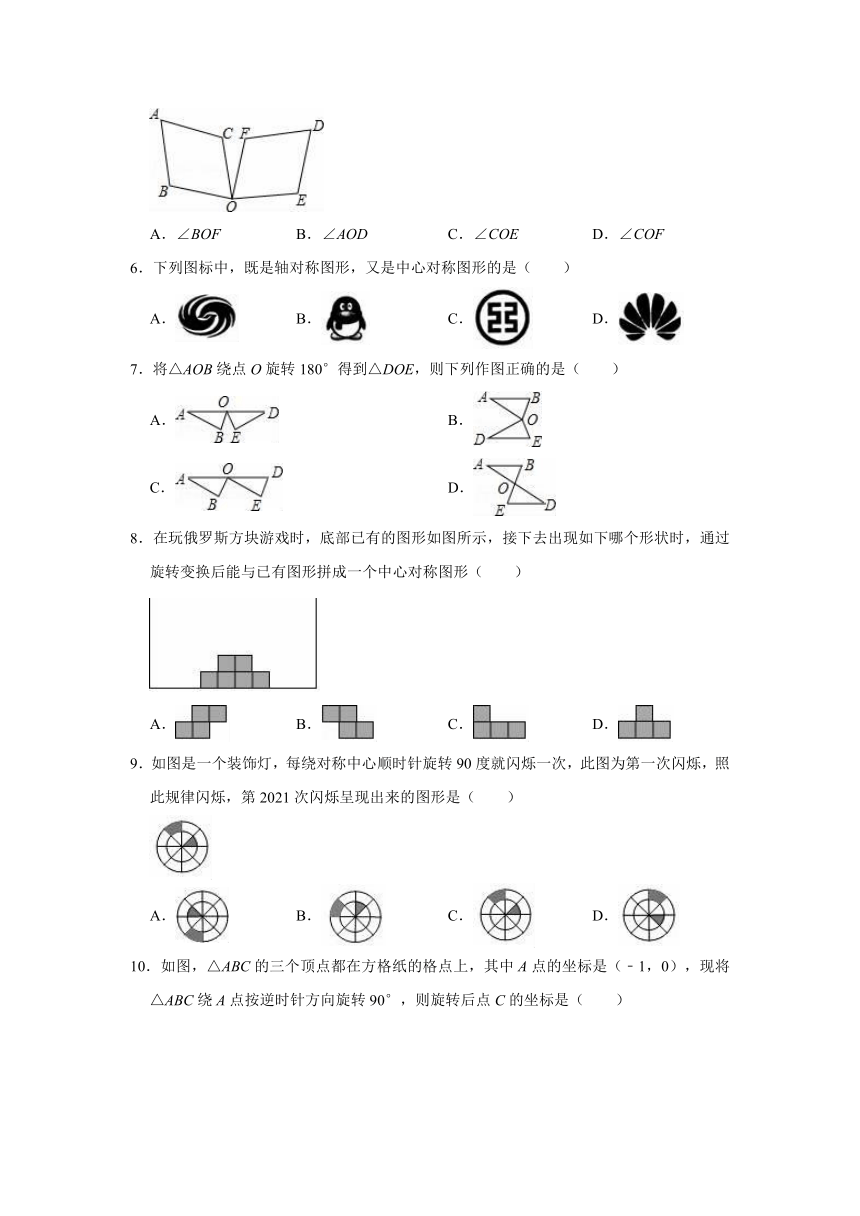
2021-2022学年沪科新版九年级下册数学《第24 圆》单元测试卷
一.选择题
1.已知⊙O中,最长的弦长为16cm,则⊙O的半径是( )
A.4cm B.8cm C.16cm D.32cm
2.如图,图案(1)变成图案(2)是由下列哪种变换而成的( )
A.平移变换 B.轴对称变换 C.旋转变换 D.相似变换
3.如图,已知菱形ABCD与菱形EFGH关于直线BD上某个点成中心对称,则点B的对称点是( )
A.点E B.点F C.点G D.点H
4.下列图形中,可以看作是中心对称图形的是( )
A. B.
C. D.
5.如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( )
A.∠BOF B.∠AOD C.∠COE D.∠COF
6.下列图标中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
7.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A. B.
C. D.
8.在玩俄罗斯方块游戏时,底部已有的图形如图所示,接下去出现如下哪个形状时,通过旋转变换后能与已有图形拼成一个中心对称图形( )
A. B. C. D.
9.如图是一个装饰灯,每绕对称中心顺时针旋转90度就闪烁一次,此图为第一次闪烁,照此规律闪烁,第2021次闪烁呈现出来的图形是( )
A. B. C. D.
10.如图,△ABC的三个顶点都在方格纸的格点上,其中A点的坐标是(﹣1,0),现将△ABC绕A点按逆时针方向旋转90°,则旋转后点C的坐标是( )
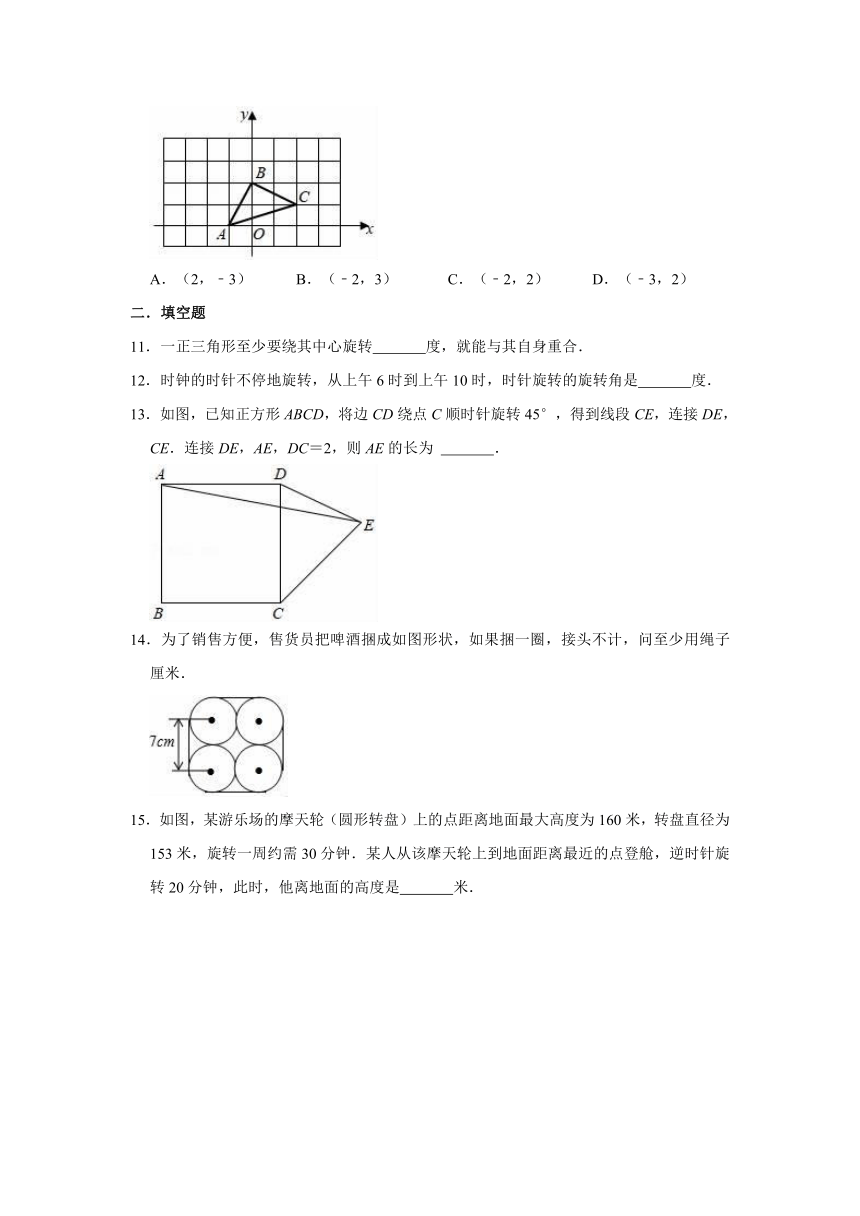
A.(2,﹣3) B.(﹣2,3) C.(﹣2,2) D.(﹣3,2)
二.填空题
11.一正三角形至少要绕其中心旋转 度,就能与其自身重合.
12.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是 度.
13.如图,已知正方形ABCD,将边CD绕点C顺时针旋转45°,得到线段CE,连接DE,CE.连接DE,AE,DC=2,则AE的长为 .
14.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子 厘米.
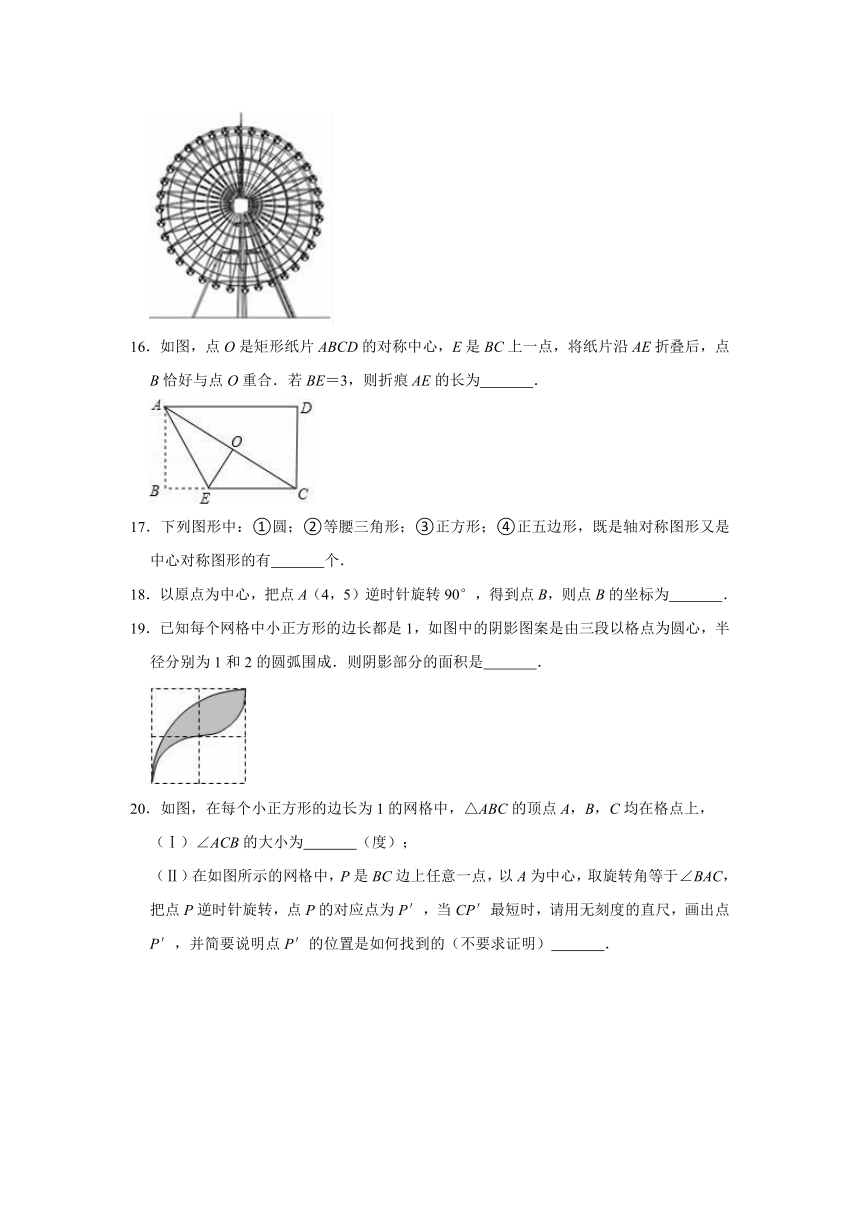
15.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是 米.
16.如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为 .
17.下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有 个.
18.以原点为中心,把点A(4,5)逆时针旋转90°,得到点B,则点B的坐标为 .
19.已知每个网格中小正方形的边长都是1,如图中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.则阴影部分的面积是 .
20.如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(Ⅰ)∠ACB的大小为 (度);
(Ⅱ)在如图所示的网格中,P是BC边上任意一点,以A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为P′,当CP′最短时,请用无刻度的直尺,画出点P′,并简要说明点P′的位置是如何找到的(不要求证明) .
三.解答题
21.如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE∥BC.
(2)若AB=8,BD=7,求△ADE的周长.
22.如图,AC是Rt△OAB斜边上的高,到点O的距离等于OA的所有点组成的图形记为G,图形G与OB交于点D,连接AD.
(1)依题意补全图形,并求证:AD平分∠BAC;
(2)如果OC=6,tanB=,求BD的长.
23.如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
24.(1)计算: +﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 个;第2008个图案是 .
25.如图,已知AD=AE,AB=AC.
(1)求证:∠B=∠C;
(2)若∠A=50°,问△ADC经过怎样的变换能与△AEB重合?
26.如图,正方形ABCD与正方形A′B′C′D′关于点O中心对称,若正方形ABCD的边长为1,图形重合部分为正方形,面积为y,线段OB的长为x,求y与x之间的函数关系式.
27.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
参考答案与试题解析
一.选择题
1.解:∵最长的弦长为16cm,
∴⊙O的直径为16cm,
∴⊙O的半径为8cm.
故选:B.
2.解:根据观察可知,图案(1)变成图案(2)是由旋转变换而成的.
故选:C.
3.解:由于四边形ABCD与四边形EFGH都是菱形,且关于直线BD上某个点成中心对称,
根据中心对称的定义可知,点B的对称点是H.
故选:D.
4.解:A.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
B.旋转180°,与原图形能够完全重合是中心对称图形;故此选项符合题意;
C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
故选:B.
5.解:A、OB旋转后的对应边为OF,故∠BOF可以作为旋转角,故本选项错误;
B、OA旋转后的对应边为OD,故∠AOD可以作为旋转角,故本选项错误;
C、OC旋转后的对应边为OE,故∠COE可以作为旋转角,故本选项错误;
D、OC旋转后的对应边为OE不是OF,故∠COF不可以作为旋转角,故本选项正确;
故选:D.
6.解:A、不是轴对称图形,是中心对称图形,故本选项不合题意;
B、既不是轴对称图形,也不是中心对称图形,故本选项不合题意;
C、既是轴对称图形,又是中心对称图形,故本选项符合题意;
D、是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:C.
7.解:△AOB与△DOE关于点O中心对称的只有D选项.
故选:D.
8.解:如图所示:只有选项D可以与已知图形组成中心对称图形.
故选:D.
9.解:由题意,每旋转一次,旋转角为90°,即每4次旋转一周,
∵2021÷4=505......1,
即第2021次与第1次的图案相同.
故选:C.
10.解:观察图象,可知C′(﹣2,3),
故选:B.
二.填空题
11.解:∵360°÷3=120°,
∴该图形绕中心至少旋转120度后能和原来的图案互相重合.
故答案为:120.
12.解:∵时针从上午的6时到10时共旋转了4个格,每相邻两个格之间的夹角是30°,
∴时针旋转的旋转角=30°×4=120°.
故答案为:120.
13.解:连接AC,
∵将边CD绕点C顺时针旋转45°,
∴∠DCE=45°,DC=CE=2,
∵四边形ABD是正方形,
∴AB=BC=DC,∠ACD=45°,
∴AC=2,∠ACE=∠ACD+∠DCE=90°,
∴AE===2.
故答案为2.
14.解:如图所示:圆的直径为:7cm.
则根据题意得:7×4+7π=28+7π≈49.98(cm)
答:捆一圈至少用绳子49.98cm.
15.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
16.解:由题意得:AB=AO=CO,即AC=2AB,
且OE垂直平分AC,
∴AE=CE,
设AB=AO=OC=x,
则有AC=2x,∠ACB=30°,
在Rt△ABC中,根据勾股定理得:BC=x,
在Rt△OEC中,∠OCE=30°,
∴OE=EC,即BE=EC,
∵BE=3,
∴OE=3,EC=6,
则AE=6,
故答案为:6
17.解:①既是轴对称图形又是中心对称图形,符合题意;
②是轴对称图形,不是中心对称图形,不符合题意;
③既是轴对称图形又是中心对称图形,符合题意;
④是轴对称图形,不是中心对称图形,不符合题意;
故既是轴对称图形又是中心对称图形的是①③共2个.
故答案为:2.
18.解:
如图,分别过A、B作x轴的垂线,垂足分别为C、D,
∵A(4,5),
∴OC=4,AC=5,
∵把点A(4,5)逆时针旋转90°得到点B,
∴OA=OB,且∠AOB=90°,
∴∠BOD+∠AOC=∠AOC+∠CAO=90°,
∴∠BOD=∠CAO,
在△AOC和△OBD中
,
∴△AOC≌△OBD(AAS),
∴OD=AC=5,BD=OC=4,
∴B(﹣5,4),
故答案为:(﹣5,4).
19.解:连接AB,阴影部分面积=S扇形AOB﹣S△ABO=﹣×2×2=π﹣2.
故答案为:π﹣2.
20.解:(1)由网格图可知,
AC=,
BC=,
AB=,
∵AC2+BC2=AB2,
∴由勾股定理逆定理,△ABC为直角三角形.
∴∠ACB=90°,
故答案为:90°.
(Ⅱ)作图过程如下:
取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求.
证明:连CF.
∵AC,CF为正方形网格对角线,
∴A、C、F共线,
∴AF=5=AB,
由图形可知:GC=,CF=2,
∵AC=,BC=,
∴△ACB∽△GCF,
∴∠GFC=∠B,
∵AF=5=AB,
∴当BC边绕点A逆时针旋转∠CAB时,点B与点F重合,点C在射线FG上.
由作图可知T为AB中点,
∴∠TCA=∠TAC,
∴∠F+∠P′CF=∠B+∠TCA=∠B+∠TAC=90°,
∴CP′⊥GF,
此时,CP′最短,
故答案为:如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求.
三.解答题
21.证明:(1)∵△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°,
∵将△BCD绕点C旋转得到△ACE.
∴CD=CE,∠ACB=∠ACE=60°,
∴△CDE是等边三角形,
∴∠CDE=60°=∠ACB,
∴DE∥BC;
(2)∵将△BCD绕点C旋转得到△ACE.
∴AE=BD=7,
∵△ADE的周长=AE+DE+AD=AE+DC+AD=AE+AC,
∴△ADE的周长=7+8=15.
22.(1)证明:如图,∵∠OAB=90°,
∴∠OAD+∠DAB=90°,
∵AC是Rt△OAB斜边上的高,
∴AC⊥OB,
∴∠ACD=∠DAC+∠ADO=90°,
∵图形G是圆O,
∴OA=OD,
∴∠OAD=∠ADO,
∴∠DAB=∠DAC,
∴AD平分∠BAC;
(2)解:∵tanB=,
∴=,
设AC=3x,BC=4x,则AB=5x,
∴=,OA=,
Rt△AOC中,∵OC=6,
∴,
解得:x=,
∵x>0,
∴x=,
∴BD=OC+BC﹣OD=6+4×﹣=.
23.解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
∵,
∴△EAB≌△DAC,
∴∠AEB=∠ADC;
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形,
∴∠AED=60°,
又∵∠AEB=∠ADC=105°,
∴∠BED=105°﹣60°=45°.
24.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
25.(1)证明:在△AEB与△ADC中,AB=AC,∠A=∠A,AE=AD;
∴△AEB≌△ADC,
∴∠B=∠C.
(2)解:先将△ADC绕点A逆时针旋转50°,
再将△ADC沿直线AE对折,即可得△ADC与△AEB重合.
或先将△ADC绕点A顺时针旋转50°,
再将△ADC沿直线AB对折,即可得△ADC与△AEB重合.
26.解:如图,设AD与C′D′交于点F,CD与A′D交于点E,
根据中心对称的性质:对称点的连线经过对称中心并且被对称中心平分,
可知四边形DED′F平行四边形,
∵∠EDF=90°,
∴四边形DED′F为矩形,
∵B,D,O共线,
∴∠EDD′=45°,
∴ED=ED′,
∴四边形DED′F是正方形,
∵正方形ABCD的边长为1,
∴BD==,
∵OB=x,
∴OD=BD﹣OB=﹣x,
∴DE==(﹣x)=2﹣x,
∴y=S正方形DED′F=DE2=(2﹣x)2.
∴y与x之间的函数关系式为:y=(2﹣x)2.
27.解:(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB=S四边形DEFC;
(2)如图所示:
(3)如图所示:
故答案为:=.
一.选择题
1.已知⊙O中,最长的弦长为16cm,则⊙O的半径是( )
A.4cm B.8cm C.16cm D.32cm
2.如图,图案(1)变成图案(2)是由下列哪种变换而成的( )
A.平移变换 B.轴对称变换 C.旋转变换 D.相似变换
3.如图,已知菱形ABCD与菱形EFGH关于直线BD上某个点成中心对称,则点B的对称点是( )
A.点E B.点F C.点G D.点H
4.下列图形中,可以看作是中心对称图形的是( )
A. B.
C. D.
5.如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( )
A.∠BOF B.∠AOD C.∠COE D.∠COF
6.下列图标中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
7.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A. B.
C. D.
8.在玩俄罗斯方块游戏时,底部已有的图形如图所示,接下去出现如下哪个形状时,通过旋转变换后能与已有图形拼成一个中心对称图形( )
A. B. C. D.
9.如图是一个装饰灯,每绕对称中心顺时针旋转90度就闪烁一次,此图为第一次闪烁,照此规律闪烁,第2021次闪烁呈现出来的图形是( )
A. B. C. D.
10.如图,△ABC的三个顶点都在方格纸的格点上,其中A点的坐标是(﹣1,0),现将△ABC绕A点按逆时针方向旋转90°,则旋转后点C的坐标是( )
A.(2,﹣3) B.(﹣2,3) C.(﹣2,2) D.(﹣3,2)
二.填空题
11.一正三角形至少要绕其中心旋转 度,就能与其自身重合.
12.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是 度.
13.如图,已知正方形ABCD,将边CD绕点C顺时针旋转45°,得到线段CE,连接DE,CE.连接DE,AE,DC=2,则AE的长为 .
14.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子 厘米.
15.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是 米.
16.如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为 .
17.下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有 个.
18.以原点为中心,把点A(4,5)逆时针旋转90°,得到点B,则点B的坐标为 .
19.已知每个网格中小正方形的边长都是1,如图中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.则阴影部分的面积是 .
20.如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(Ⅰ)∠ACB的大小为 (度);
(Ⅱ)在如图所示的网格中,P是BC边上任意一点,以A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为P′,当CP′最短时,请用无刻度的直尺,画出点P′,并简要说明点P′的位置是如何找到的(不要求证明) .
三.解答题
21.如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE∥BC.
(2)若AB=8,BD=7,求△ADE的周长.
22.如图,AC是Rt△OAB斜边上的高,到点O的距离等于OA的所有点组成的图形记为G,图形G与OB交于点D,连接AD.
(1)依题意补全图形,并求证:AD平分∠BAC;
(2)如果OC=6,tanB=,求BD的长.
23.如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
24.(1)计算: +﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 个;第2008个图案是 .
25.如图,已知AD=AE,AB=AC.
(1)求证:∠B=∠C;
(2)若∠A=50°,问△ADC经过怎样的变换能与△AEB重合?
26.如图,正方形ABCD与正方形A′B′C′D′关于点O中心对称,若正方形ABCD的边长为1,图形重合部分为正方形,面积为y,线段OB的长为x,求y与x之间的函数关系式.
27.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
参考答案与试题解析
一.选择题
1.解:∵最长的弦长为16cm,
∴⊙O的直径为16cm,
∴⊙O的半径为8cm.
故选:B.
2.解:根据观察可知,图案(1)变成图案(2)是由旋转变换而成的.
故选:C.
3.解:由于四边形ABCD与四边形EFGH都是菱形,且关于直线BD上某个点成中心对称,
根据中心对称的定义可知,点B的对称点是H.
故选:D.
4.解:A.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
B.旋转180°,与原图形能够完全重合是中心对称图形;故此选项符合题意;
C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
故选:B.
5.解:A、OB旋转后的对应边为OF,故∠BOF可以作为旋转角,故本选项错误;
B、OA旋转后的对应边为OD,故∠AOD可以作为旋转角,故本选项错误;
C、OC旋转后的对应边为OE,故∠COE可以作为旋转角,故本选项错误;
D、OC旋转后的对应边为OE不是OF,故∠COF不可以作为旋转角,故本选项正确;
故选:D.
6.解:A、不是轴对称图形,是中心对称图形,故本选项不合题意;
B、既不是轴对称图形,也不是中心对称图形,故本选项不合题意;
C、既是轴对称图形,又是中心对称图形,故本选项符合题意;
D、是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:C.
7.解:△AOB与△DOE关于点O中心对称的只有D选项.
故选:D.
8.解:如图所示:只有选项D可以与已知图形组成中心对称图形.
故选:D.
9.解:由题意,每旋转一次,旋转角为90°,即每4次旋转一周,
∵2021÷4=505......1,
即第2021次与第1次的图案相同.
故选:C.
10.解:观察图象,可知C′(﹣2,3),
故选:B.
二.填空题
11.解:∵360°÷3=120°,
∴该图形绕中心至少旋转120度后能和原来的图案互相重合.
故答案为:120.
12.解:∵时针从上午的6时到10时共旋转了4个格,每相邻两个格之间的夹角是30°,
∴时针旋转的旋转角=30°×4=120°.
故答案为:120.
13.解:连接AC,
∵将边CD绕点C顺时针旋转45°,
∴∠DCE=45°,DC=CE=2,
∵四边形ABD是正方形,
∴AB=BC=DC,∠ACD=45°,
∴AC=2,∠ACE=∠ACD+∠DCE=90°,
∴AE===2.
故答案为2.
14.解:如图所示:圆的直径为:7cm.
则根据题意得:7×4+7π=28+7π≈49.98(cm)
答:捆一圈至少用绳子49.98cm.
15.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
16.解:由题意得:AB=AO=CO,即AC=2AB,
且OE垂直平分AC,
∴AE=CE,
设AB=AO=OC=x,
则有AC=2x,∠ACB=30°,
在Rt△ABC中,根据勾股定理得:BC=x,
在Rt△OEC中,∠OCE=30°,
∴OE=EC,即BE=EC,
∵BE=3,
∴OE=3,EC=6,
则AE=6,
故答案为:6
17.解:①既是轴对称图形又是中心对称图形,符合题意;
②是轴对称图形,不是中心对称图形,不符合题意;
③既是轴对称图形又是中心对称图形,符合题意;
④是轴对称图形,不是中心对称图形,不符合题意;
故既是轴对称图形又是中心对称图形的是①③共2个.
故答案为:2.
18.解:
如图,分别过A、B作x轴的垂线,垂足分别为C、D,
∵A(4,5),
∴OC=4,AC=5,
∵把点A(4,5)逆时针旋转90°得到点B,
∴OA=OB,且∠AOB=90°,
∴∠BOD+∠AOC=∠AOC+∠CAO=90°,
∴∠BOD=∠CAO,
在△AOC和△OBD中
,
∴△AOC≌△OBD(AAS),
∴OD=AC=5,BD=OC=4,
∴B(﹣5,4),
故答案为:(﹣5,4).
19.解:连接AB,阴影部分面积=S扇形AOB﹣S△ABO=﹣×2×2=π﹣2.
故答案为:π﹣2.
20.解:(1)由网格图可知,
AC=,
BC=,
AB=,
∵AC2+BC2=AB2,
∴由勾股定理逆定理,△ABC为直角三角形.
∴∠ACB=90°,
故答案为:90°.
(Ⅱ)作图过程如下:
取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求.
证明:连CF.
∵AC,CF为正方形网格对角线,
∴A、C、F共线,
∴AF=5=AB,
由图形可知:GC=,CF=2,
∵AC=,BC=,
∴△ACB∽△GCF,
∴∠GFC=∠B,
∵AF=5=AB,
∴当BC边绕点A逆时针旋转∠CAB时,点B与点F重合,点C在射线FG上.
由作图可知T为AB中点,
∴∠TCA=∠TAC,
∴∠F+∠P′CF=∠B+∠TCA=∠B+∠TAC=90°,
∴CP′⊥GF,
此时,CP′最短,
故答案为:如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求.
三.解答题
21.证明:(1)∵△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°,
∵将△BCD绕点C旋转得到△ACE.
∴CD=CE,∠ACB=∠ACE=60°,
∴△CDE是等边三角形,
∴∠CDE=60°=∠ACB,
∴DE∥BC;
(2)∵将△BCD绕点C旋转得到△ACE.
∴AE=BD=7,
∵△ADE的周长=AE+DE+AD=AE+DC+AD=AE+AC,
∴△ADE的周长=7+8=15.
22.(1)证明:如图,∵∠OAB=90°,
∴∠OAD+∠DAB=90°,
∵AC是Rt△OAB斜边上的高,
∴AC⊥OB,
∴∠ACD=∠DAC+∠ADO=90°,
∵图形G是圆O,
∴OA=OD,
∴∠OAD=∠ADO,
∴∠DAB=∠DAC,
∴AD平分∠BAC;
(2)解:∵tanB=,
∴=,
设AC=3x,BC=4x,则AB=5x,
∴=,OA=,
Rt△AOC中,∵OC=6,
∴,
解得:x=,
∵x>0,
∴x=,
∴BD=OC+BC﹣OD=6+4×﹣=.
23.解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
∵,
∴△EAB≌△DAC,
∴∠AEB=∠ADC;
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形,
∴∠AED=60°,
又∵∠AEB=∠ADC=105°,
∴∠BED=105°﹣60°=45°.
24.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
25.(1)证明:在△AEB与△ADC中,AB=AC,∠A=∠A,AE=AD;
∴△AEB≌△ADC,
∴∠B=∠C.
(2)解:先将△ADC绕点A逆时针旋转50°,
再将△ADC沿直线AE对折,即可得△ADC与△AEB重合.
或先将△ADC绕点A顺时针旋转50°,
再将△ADC沿直线AB对折,即可得△ADC与△AEB重合.
26.解:如图,设AD与C′D′交于点F,CD与A′D交于点E,
根据中心对称的性质:对称点的连线经过对称中心并且被对称中心平分,
可知四边形DED′F平行四边形,
∵∠EDF=90°,
∴四边形DED′F为矩形,
∵B,D,O共线,
∴∠EDD′=45°,
∴ED=ED′,
∴四边形DED′F是正方形,
∵正方形ABCD的边长为1,
∴BD==,
∵OB=x,
∴OD=BD﹣OB=﹣x,
∴DE==(﹣x)=2﹣x,
∴y=S正方形DED′F=DE2=(2﹣x)2.
∴y与x之间的函数关系式为:y=(2﹣x)2.
27.解:(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB=S四边形DEFC;
(2)如图所示:
(3)如图所示:
故答案为:=.
