2021-2022学年鲁教版六年级下册数学第7章相交线与平行线单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版六年级下册数学第7章相交线与平行线单元测试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 16:23:23 | ||
图片预览


文档简介
2021-2022学年鲁教五四新版六年级下册数学《第7章 相交线与平行线》单元测试卷
一.选择题
1.平面内有两两相交的三条直线,若最多有m个交点,最少有n个交点,则m+n等于( )
A.1 B.2 C.3 D.4
2.在同一平面内两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行
C.平行或相交 D.平行或相交或重合
3.下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A.1个 B.2个 C.3个 D.4个
4.如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
A.44° B.45° C.46° D.56°
5.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c
C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c
6.下列说法中不正确的有( )
①两条不相交的直线叫做平行线;
②经过一点,有且只有一条直线与已知直线垂直;
③经过一点,有且只有一条直线与已知直线平行;
④一个角的两边与另一个角两边互相垂直,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
7.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
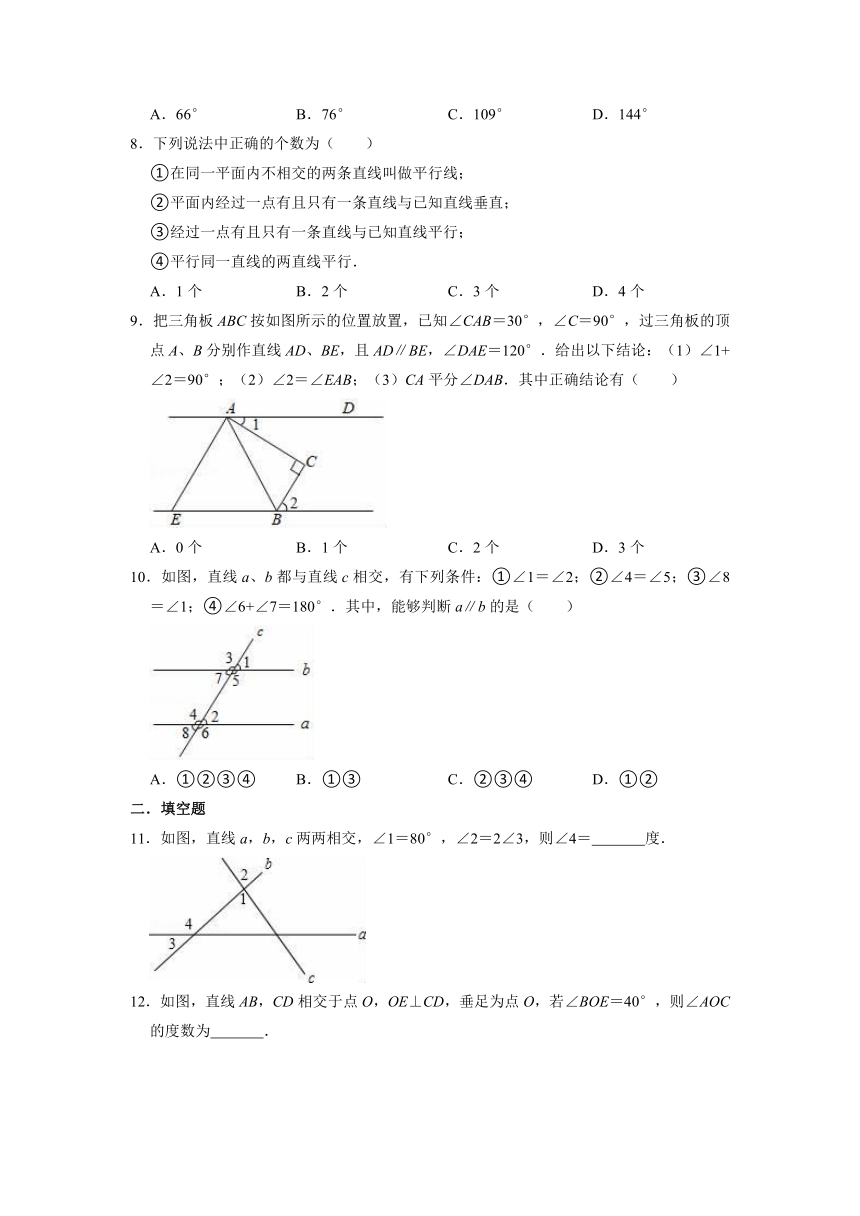
8.下列说法中正确的个数为( )
①在同一平面内不相交的两条直线叫做平行线;
②平面内经过一点有且只有一条直线与已知直线垂直;
③经过一点有且只有一条直线与已知直线平行;
④平行同一直线的两直线平行.
A.1个 B.2个 C.3个 D.4个
9.把三角板ABC按如图所示的位置放置,已知∠CAB=30°,∠C=90°,过三角板的顶点A、B分别作直线AD、BE,且AD∥BE,∠DAE=120°.给出以下结论:(1)∠1+∠2=90°;(2)∠2=∠EAB;(3)CA平分∠DAB.其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
10.如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠4=∠5;③∠8=∠1;④∠6+∠7=180°.其中,能够判断a∥b的是( )
A.①②③④ B.①③ C.②③④ D.①②
二.填空题
11.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4= 度.
12.如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠BOE=40°,则∠AOC的度数为 .
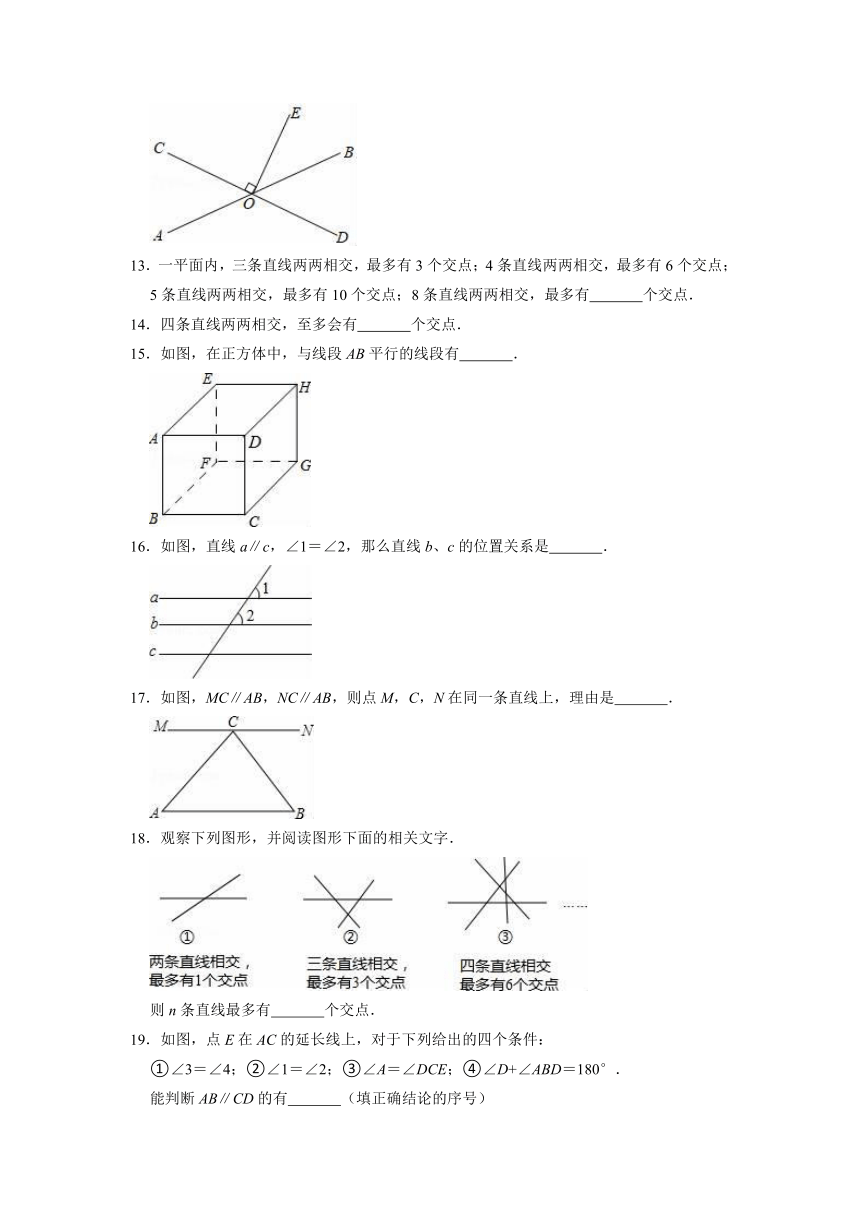
13.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
14.四条直线两两相交,至多会有 个交点.
15.如图,在正方体中,与线段AB平行的线段有 .
16.如图,直线a∥c,∠1=∠2,那么直线b、c的位置关系是 .
17.如图,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是 .
18.观察下列图形,并阅读图形下面的相关文字.
则n条直线最多有 个交点.
19.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有 (填正确结论的序号)
20.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
三.解答题
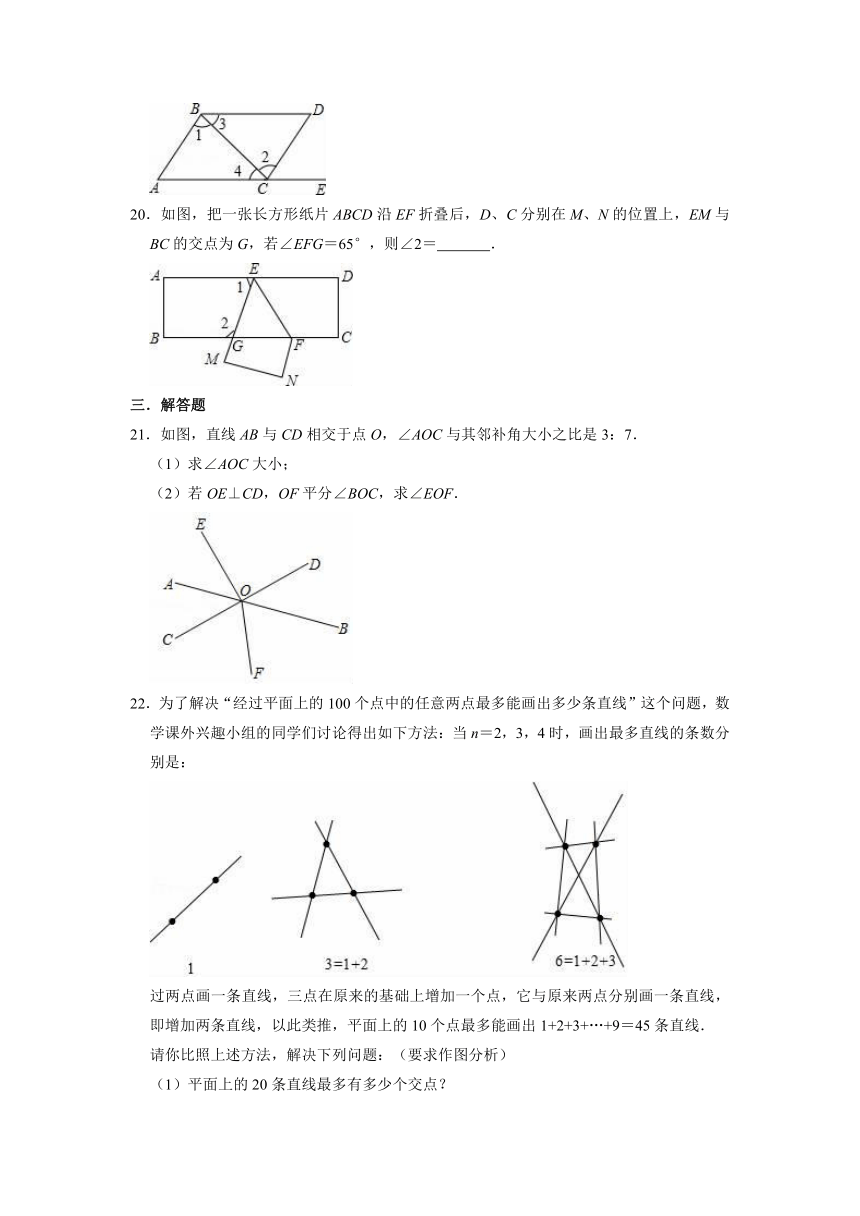
21.如图,直线AB与CD相交于点O,∠AOC与其邻补角大小之比是3:7.
(1)求∠AOC大小;
(2)若OE⊥CD,OF平分∠BOC,求∠EOF.
22.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?
23.如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=26°,求∠AOE和∠COE的度数.
24.(1)直线l1与l2是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第三条直线l3,则这三条直线最多有 个交点;
(2)如果在(1)的基础上在这个平面内再画第四条直线l4,则这四条直线最多可有 个交点.
(3)由(1)(2)我们可以猜想:在同一平面内,n(n>1)条直线最多有 个交点.
25.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
26.画图题:
(1)在如图所示的方格纸中(单位长度为1),经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 .
(3)连接AC和BC,则三角形ABC的面积是 .
27.如图1,已知AC∥BD,点P是直线AC,BD间的一点,连接AB,AP,BP,过点P作直线MN∥AC.
(1)MN与BD的位置关系是什么,请说明理由;
(2)试说明∠APB=∠PBD+∠PAC;
(3)如图2,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.
参考答案与试题解析
一.选择题
1.解:平面内两两相交的三条直线,最多有3个交点,最少有1个交点,即m=3,n=1,
∴m+n=4.
故选:D.
2.解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故选:C.
3.解:①过两点有且只有一条直线,故①正确;
②两直线相交只有一个交点,故②正确;
③0的绝对值是它本身,故③正确;
④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.
故选:C.
4.解:由OM⊥l1,
∴α+90°+β=180°,
∴α=46°,
故选:C.
5.解:A、如果a∥b,a⊥c,那么b⊥c,说法正确;
B、如果b∥a,c∥a,那么b∥c,说法正确;
C、如果b⊥a,c⊥a,那么b⊥c,说法错误;
D、如果b⊥a,c⊥a,那么b∥c,说法正确;
故选:C.
6.解:①两条不相交的直线叫做平行线是在同一平面内才可以成立的,故错误.
②在同一平面内,经过一点有且只有一条直线与已知直线垂直,故错误;
③经过直线外一点,有且只有一条直线与这条直线平行,故错误;
④一个角的两边与另一个角两边互相垂直,那么这两个角相等或互补,故错误.
故选:D.
7.解:∵∠1=38°,
∴∠AOD=180°﹣∠1=142°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=71°,
∴∠COE=180°﹣∠DOE=109°,
故选:C.
8.解:①在同一平面内不相交的两条直线叫做平行线是正确的,同一平面内的两条直线不相交即平行.
②平面内经过一点有且只有一条直线与已知直线垂直是正确的.
③经过一点有且只有一条直线与已知直线平行,应强调在经过直线外一点,故是错误的.
④满足平行公理的推论,正确.
故选:C.
9.解:∵AD∥BE,
∴(∠1+∠CAB)+(∠2+∠ABC)=180°,
∵∠C=90°,
∴∠CAB+∠ABC=90°,
∴∠1+∠2=90°,
故(1)正确,符合题意;
∵∠EAB=∠DAE﹣∠CAB﹣∠1,∠CAB=30°,∠DAE=120°,
∴∠EAB=90°﹣∠1,
∵∠1+∠2=90°,
∴∠2=90°﹣∠1,
∴∠2=∠EAB,
故(2)正确,符合题意;
∵∠1=∠DAE﹣∠CAB﹣∠EAB=90°﹣∠EAB,
∴∠1的大小随∠EAB的大小变化而变化,
∵∠CAB=30°固定,
∴CA不一定平分∠DAB,
故(3)错误,不符合题意;
综上,正确符合题意的结论有2个,
故选:C.
10.解:①∵∠1=∠2,
∴a∥b,故本小题正确;
②∵4=∠5,
∴a∥b,故本小题正确;
③∵∠8=∠1,∠8=∠2,
∴∠1=∠2,
∴a∥b,故本小题正确;
④∵∠6+∠7=180°,∠6+∠2=180°,
∴∠7=∠2,
∴a∥b,故本小题正确.
故选:A.
二.填空题
11.解:∵∠1与∠2是对顶角,
∴∠1=∠2=80°,
又已知∠2=2∠3,
∴∠3=40°.
∵∠4与∠3互为邻补角,
∴∠4=180°﹣∠3=180°﹣40°=140°.
12.解:∵OE⊥CD,
∴∠EOD=90°,
∵∠BOE=40°,
∴∠BOD=90°﹣40°=50°,
∴∠AOC=∠BOD=50°.
故答案为:50°.
13.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,
∴8条直线两两相交,交点的个数最多为=28.
故答案为:28.
14.解:如图,可看出四条直线两两相交,至多有6个交点.
故填:6.
15.解:与AB平行的线段是:DC、EF;
与CD平行的线段是:HG,
所以与AB线段平行的线段有:EF、HG、DC.
故答案是:EF、HG、DC.
16.解:∵∠1=∠2,
∴a∥b,
∵a∥c,
∴b∥c.
故答案为:b∥c.
17.解:∵MC∥AB,NC∥AB,∴点M,C,N在同一条直线上,
理由是:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
18.解:∵两条直线相交,最多有1个交点,即1=,
三条直线两条直线相交,最多有3个交点,即3=
四条直线相交,最多有6个交点,即6=
5条直线相交,最多有10个交点,即5=,
∴n条直线相交,最多的交点个数是,
故答案为:.
19.解:①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故答案为②③④.
20.解:∵长方形纸片ABCD的边AD∥BC,
∴∠3=∠EFG=65°,
根据翻折的性质,可得∠1=180°﹣2∠3=180°﹣2×65°=50°,
又∵AD∥BC,
∴∠2=180°﹣∠1=180°﹣50°=130°.
故答案为:130°.
三.解答题
21.解:(1)∵∠AOC与其邻补角大小之比是3:7,
设∠AOC=3x°,则其邻补角为7x°,
∴3x+7x=180,
∴x=18,
∴3x=54,
即∠AOC=54°.
(2)∵OE⊥CD,
∴∠EOC=90°,
∵∠AOC=54°,
∴∠BOC=180°﹣∠AOC=180°﹣54°=126°,
∵OF平分∠BOC,
∴∠COF=∠BOC=63°,
∴∠EOF=∠EOC+∠COF=90°+63°=153°.
22.解:(1)当有2,3,4条直线时最多交点的个数分别是:
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分,
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=1+=.
23.解:∵∠AOC=26°,
∴∠AOD=180°﹣∠AOC=154°,
∵OE是∠AOD的平分线,
∴∠AOE=∠DOE=∠AOD=77°,
∴∠COE=180°﹣∠DOE=103°.
24.解:(1)三条直线相交交点最多为:1+2=3;
(2)四条直线相交交点最多为:1+2+3=6;
(3)五条直线相交交点最多为:1+2+3+4=10;
六条直线相交交点最多为:1+2+3+4+5=15;
…;
n条直线相交交点最多为:1+2+3+…+n﹣1=.
故答案为:3,6,.
25.解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
26.解:(1)如图
(2)EF与GH的位置关系是:垂直;
(3)设小方格的边长是1,则
AB=2,CH=2,
∴S△ABC=×2×2=10.
27.解:(1)平行; 理由如下:
∵AC∥BD,MN∥AC,
∴MN∥BD;
(2)∵AC∥BD,MN∥BD,
∴∠PBD=∠1,∠PAC=∠2,
∴∠APB=∠1+∠2=∠PBD+∠PAC.
(3)答:不成立.
它们的关系是∠APB=∠PBD﹣∠PAC.
理由是:如图2,过点P作PQ∥AC,
∵AC∥BD,
∴PQ∥AC∥BD,
∴∠PAC=∠APQ,∠PBD=∠BPQ,
∴∠APB=∠BPQ﹣∠APQ=∠PBD﹣∠PAC.
一.选择题
1.平面内有两两相交的三条直线,若最多有m个交点,最少有n个交点,则m+n等于( )
A.1 B.2 C.3 D.4
2.在同一平面内两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行
C.平行或相交 D.平行或相交或重合
3.下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A.1个 B.2个 C.3个 D.4个
4.如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
A.44° B.45° C.46° D.56°
5.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c
C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c
6.下列说法中不正确的有( )
①两条不相交的直线叫做平行线;
②经过一点,有且只有一条直线与已知直线垂直;
③经过一点,有且只有一条直线与已知直线平行;
④一个角的两边与另一个角两边互相垂直,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
7.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
8.下列说法中正确的个数为( )
①在同一平面内不相交的两条直线叫做平行线;
②平面内经过一点有且只有一条直线与已知直线垂直;
③经过一点有且只有一条直线与已知直线平行;
④平行同一直线的两直线平行.
A.1个 B.2个 C.3个 D.4个
9.把三角板ABC按如图所示的位置放置,已知∠CAB=30°,∠C=90°,过三角板的顶点A、B分别作直线AD、BE,且AD∥BE,∠DAE=120°.给出以下结论:(1)∠1+∠2=90°;(2)∠2=∠EAB;(3)CA平分∠DAB.其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
10.如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠4=∠5;③∠8=∠1;④∠6+∠7=180°.其中,能够判断a∥b的是( )
A.①②③④ B.①③ C.②③④ D.①②
二.填空题
11.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4= 度.
12.如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠BOE=40°,则∠AOC的度数为 .
13.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
14.四条直线两两相交,至多会有 个交点.
15.如图,在正方体中,与线段AB平行的线段有 .
16.如图,直线a∥c,∠1=∠2,那么直线b、c的位置关系是 .
17.如图,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是 .
18.观察下列图形,并阅读图形下面的相关文字.
则n条直线最多有 个交点.
19.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有 (填正确结论的序号)
20.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
三.解答题
21.如图,直线AB与CD相交于点O,∠AOC与其邻补角大小之比是3:7.
(1)求∠AOC大小;
(2)若OE⊥CD,OF平分∠BOC,求∠EOF.
22.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?
23.如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=26°,求∠AOE和∠COE的度数.
24.(1)直线l1与l2是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第三条直线l3,则这三条直线最多有 个交点;
(2)如果在(1)的基础上在这个平面内再画第四条直线l4,则这四条直线最多可有 个交点.
(3)由(1)(2)我们可以猜想:在同一平面内,n(n>1)条直线最多有 个交点.
25.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
26.画图题:
(1)在如图所示的方格纸中(单位长度为1),经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 .
(3)连接AC和BC,则三角形ABC的面积是 .
27.如图1,已知AC∥BD,点P是直线AC,BD间的一点,连接AB,AP,BP,过点P作直线MN∥AC.
(1)MN与BD的位置关系是什么,请说明理由;
(2)试说明∠APB=∠PBD+∠PAC;
(3)如图2,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.
参考答案与试题解析
一.选择题
1.解:平面内两两相交的三条直线,最多有3个交点,最少有1个交点,即m=3,n=1,
∴m+n=4.
故选:D.
2.解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故选:C.
3.解:①过两点有且只有一条直线,故①正确;
②两直线相交只有一个交点,故②正确;
③0的绝对值是它本身,故③正确;
④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.
故选:C.
4.解:由OM⊥l1,
∴α+90°+β=180°,
∴α=46°,
故选:C.
5.解:A、如果a∥b,a⊥c,那么b⊥c,说法正确;
B、如果b∥a,c∥a,那么b∥c,说法正确;
C、如果b⊥a,c⊥a,那么b⊥c,说法错误;
D、如果b⊥a,c⊥a,那么b∥c,说法正确;
故选:C.
6.解:①两条不相交的直线叫做平行线是在同一平面内才可以成立的,故错误.
②在同一平面内,经过一点有且只有一条直线与已知直线垂直,故错误;
③经过直线外一点,有且只有一条直线与这条直线平行,故错误;
④一个角的两边与另一个角两边互相垂直,那么这两个角相等或互补,故错误.
故选:D.
7.解:∵∠1=38°,
∴∠AOD=180°﹣∠1=142°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=71°,
∴∠COE=180°﹣∠DOE=109°,
故选:C.
8.解:①在同一平面内不相交的两条直线叫做平行线是正确的,同一平面内的两条直线不相交即平行.
②平面内经过一点有且只有一条直线与已知直线垂直是正确的.
③经过一点有且只有一条直线与已知直线平行,应强调在经过直线外一点,故是错误的.
④满足平行公理的推论,正确.
故选:C.
9.解:∵AD∥BE,
∴(∠1+∠CAB)+(∠2+∠ABC)=180°,
∵∠C=90°,
∴∠CAB+∠ABC=90°,
∴∠1+∠2=90°,
故(1)正确,符合题意;
∵∠EAB=∠DAE﹣∠CAB﹣∠1,∠CAB=30°,∠DAE=120°,
∴∠EAB=90°﹣∠1,
∵∠1+∠2=90°,
∴∠2=90°﹣∠1,
∴∠2=∠EAB,
故(2)正确,符合题意;
∵∠1=∠DAE﹣∠CAB﹣∠EAB=90°﹣∠EAB,
∴∠1的大小随∠EAB的大小变化而变化,
∵∠CAB=30°固定,
∴CA不一定平分∠DAB,
故(3)错误,不符合题意;
综上,正确符合题意的结论有2个,
故选:C.
10.解:①∵∠1=∠2,
∴a∥b,故本小题正确;
②∵4=∠5,
∴a∥b,故本小题正确;
③∵∠8=∠1,∠8=∠2,
∴∠1=∠2,
∴a∥b,故本小题正确;
④∵∠6+∠7=180°,∠6+∠2=180°,
∴∠7=∠2,
∴a∥b,故本小题正确.
故选:A.
二.填空题
11.解:∵∠1与∠2是对顶角,
∴∠1=∠2=80°,
又已知∠2=2∠3,
∴∠3=40°.
∵∠4与∠3互为邻补角,
∴∠4=180°﹣∠3=180°﹣40°=140°.
12.解:∵OE⊥CD,
∴∠EOD=90°,
∵∠BOE=40°,
∴∠BOD=90°﹣40°=50°,
∴∠AOC=∠BOD=50°.
故答案为:50°.
13.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,
∴8条直线两两相交,交点的个数最多为=28.
故答案为:28.
14.解:如图,可看出四条直线两两相交,至多有6个交点.
故填:6.
15.解:与AB平行的线段是:DC、EF;
与CD平行的线段是:HG,
所以与AB线段平行的线段有:EF、HG、DC.
故答案是:EF、HG、DC.
16.解:∵∠1=∠2,
∴a∥b,
∵a∥c,
∴b∥c.
故答案为:b∥c.
17.解:∵MC∥AB,NC∥AB,∴点M,C,N在同一条直线上,
理由是:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
18.解:∵两条直线相交,最多有1个交点,即1=,
三条直线两条直线相交,最多有3个交点,即3=
四条直线相交,最多有6个交点,即6=
5条直线相交,最多有10个交点,即5=,
∴n条直线相交,最多的交点个数是,
故答案为:.
19.解:①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故答案为②③④.
20.解:∵长方形纸片ABCD的边AD∥BC,
∴∠3=∠EFG=65°,
根据翻折的性质,可得∠1=180°﹣2∠3=180°﹣2×65°=50°,
又∵AD∥BC,
∴∠2=180°﹣∠1=180°﹣50°=130°.
故答案为:130°.
三.解答题
21.解:(1)∵∠AOC与其邻补角大小之比是3:7,
设∠AOC=3x°,则其邻补角为7x°,
∴3x+7x=180,
∴x=18,
∴3x=54,
即∠AOC=54°.
(2)∵OE⊥CD,
∴∠EOC=90°,
∵∠AOC=54°,
∴∠BOC=180°﹣∠AOC=180°﹣54°=126°,
∵OF平分∠BOC,
∴∠COF=∠BOC=63°,
∴∠EOF=∠EOC+∠COF=90°+63°=153°.
22.解:(1)当有2,3,4条直线时最多交点的个数分别是:
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分,
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=1+=.
23.解:∵∠AOC=26°,
∴∠AOD=180°﹣∠AOC=154°,
∵OE是∠AOD的平分线,
∴∠AOE=∠DOE=∠AOD=77°,
∴∠COE=180°﹣∠DOE=103°.
24.解:(1)三条直线相交交点最多为:1+2=3;
(2)四条直线相交交点最多为:1+2+3=6;
(3)五条直线相交交点最多为:1+2+3+4=10;
六条直线相交交点最多为:1+2+3+4+5=15;
…;
n条直线相交交点最多为:1+2+3+…+n﹣1=.
故答案为:3,6,.
25.解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
26.解:(1)如图
(2)EF与GH的位置关系是:垂直;
(3)设小方格的边长是1,则
AB=2,CH=2,
∴S△ABC=×2×2=10.
27.解:(1)平行; 理由如下:
∵AC∥BD,MN∥AC,
∴MN∥BD;
(2)∵AC∥BD,MN∥BD,
∴∠PBD=∠1,∠PAC=∠2,
∴∠APB=∠1+∠2=∠PBD+∠PAC.
(3)答:不成立.
它们的关系是∠APB=∠PBD﹣∠PAC.
理由是:如图2,过点P作PQ∥AC,
∵AC∥BD,
∴PQ∥AC∥BD,
∴∠PAC=∠APQ,∠PBD=∠BPQ,
∴∠APB=∠BPQ﹣∠APQ=∠PBD﹣∠PAC.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
