小学数学人教版五年级下册2 因数与倍数2.1因数和倍数同步练习及答案
文档属性
| 名称 | 小学数学人教版五年级下册2 因数与倍数2.1因数和倍数同步练习及答案 | 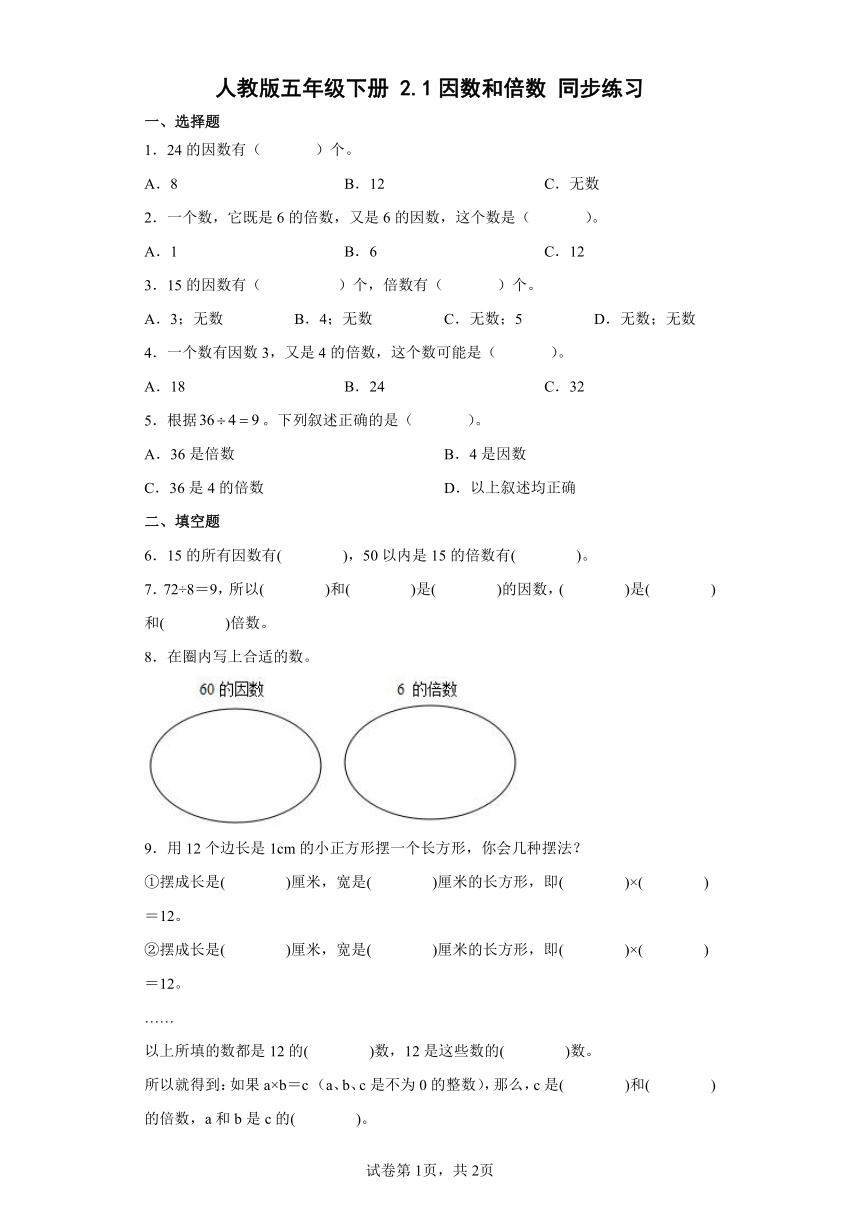 | |
| 格式 | docx | ||
| 文件大小 | 70.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 17:24:16 | ||
图片预览





文档简介
人教版五年级下册 2.1因数和倍数 同步练习
一、选择题
1.24的因数有( )个。
A.8 B.12 C.无数
2.一个数,它既是6的倍数,又是6的因数,这个数是( )。
A.1 B.6 C.12
3.15的因数有( )个,倍数有( )个。
A.3;无数 B.4;无数 C.无数;5 D.无数;无数
4.一个数有因数3,又是4的倍数,这个数可能是( )。
A.18 B.24 C.32
5.根据。下列叙述正确的是( )。
A.36是倍数 B.4是因数
C.36是4的倍数 D.以上叙述均正确
二、填空题
6.15的所有因数有( ),50以内是15的倍数有( )。
7.72÷8=9,所以( )和( )是( )的因数,( )是( )和( )倍数。
8.在圈内写上合适的数。
9.用12个边长是1cm的小正方形摆一个长方形,你会几种摆法?
①摆成长是( )厘米,宽是( )厘米的长方形,即( )×( )=12。
②摆成长是( )厘米,宽是( )厘米的长方形,即( )×( )=12。
……
以上所填的数都是12的( )数,12是这些数的( )数。
所以就得到:如果a×b=c (a、b、c是不为0的整数),那么,c是( )和( )的倍数,a和b是c的( )。
三、判断题
10.1是所有非零自然数的因数。( )
11.4×7=28,28是倍数,4和7是因数。( )
12.4是0.5的倍数。( )
13.一个数的因数总比它的倍数小。( )
14.因为78=56,所以56是7和8的倍数,7和8是56的因数。( )
四、解答题
15.6的因数有1、2、3、6,这几个因数的关系是:1+2+3=6。像6这样的数,叫做完全数(也叫完美数)。小明说:28也是完全数。他说的对吗?请写出你的验证过程。
16.五(1)班有多少名同学?
17.体操表演队由48名同学组成,表演时要排成长方形队形,都可以怎样排?(至少写出3种排法)
18.李奶奶过生日时买来了70多个苹果。如果每盘装4个,正好装完;如果每盘装6个,也正好装完。
19.学校组建合唱团,五年级有48人报名,六年级有54人报名。老师准备把两个年级的同学分别分成若干小组进行训练。
(1)要使两个年级每个小组的人数相同,每组最多有多少人?
(2)暑假期间有一个紧急演出,老师需要尽快通知到每一个队员。如果采用打电话的方式,每分钟通知1人,最少要花( )分钟才能通知到每个人。(直接填出答案即可)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
找因数,从最小的自然数1找起,一直找到它本身,一对对找。
【详解】
24的因数有:1、2、3、4、6、8、12、24,共8个。
故答案为:A
【点睛】
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
2.B
【解析】
【分析】
一个数只有本身既是自己的因数,也是自己的倍数。据此解题。
【详解】
一个数,它既是6的倍数,又是6的因数,这个数是6。
故答案为:B
【点睛】
本题考查了因数和倍数,掌握因数和倍数的特征和求法是解题的关键。
3.B
【解析】
【分析】
找一个数的因数,可以一对一对的找,把15写成两个数的乘积,那么每一个乘积中的因数都是15的因数,然后从小到大依次写出即可;
15的倍数,15乘1、2、3……;有无数个。
【详解】
15的因数有1,3,5,15(4)个,倍数有(无数)个。
故答案选:B。
【点睛】
理解掌握找一个数的因数、倍数的方法是关键。
4.B
【解析】
【分析】
分别看看每个选项中的数是否符合有因数3,又是4的倍数即可。
【详解】
A.18有因数3,但不是4的倍数;
B.24既有因数3,又是4的倍数;
C.32是4的倍数,但没有因数3;
故答案为:B。
【点睛】
本题较易,熟练掌握求一个数的因数与倍数的方法是解答本题的关键。
5.C
【解析】
【分析】
如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;据此选择即可。
【详解】
根据,我们可以说36是4和9的倍数,4和9是36的因数;不能说36是倍数,4和9是因数。
故答案为:C
【点睛】
解答此题要明确:因数和倍数是相互依存的,不能单独存在。
6. 1、3、5、15 15、30、45
【解析】
【分析】
找一个数的因数,可以一对一对的找,把15写成两个数的乘积,那么每一个乘积中的因数都是20的因数,然后从小到大依次写出即可;
15的倍数,15乘1、2、3……;
【详解】
15的所有因数有1、3、5、15,50以内是15的倍数有15、30、45。
【点睛】
解答此题应根据找一个数因数和倍数的方法进行解答。
7. 8 9 72 72 8 9
【解析】
【分析】
根据因数和倍数的意义,当a÷b=c(a、b、c为非0自然数)我们说a是b和c的倍数,b和c是a的因数。据此解答。
【详解】
72÷8=9,所以(8)和(9)是(72)的因数,(72)是(8)和(9)倍数。
【点睛】
掌握因数和倍数的意义是解题的关键。
8.见详解
【解析】
【分析】
60的因数从1开始依次计算,就能一对一对的找出来;6的倍数有无数个。
【详解】
【点睛】
一个数的因数是有限个,从小到大依次列出就能不重不漏;一个数的倍数有无数个。
9. 12 1 12 1 6 2 6 2 因 倍 a b 因
【解析】
【分析】
(1)长方形的长为12厘米,宽为1厘米;
长方形的长为6厘米,宽为2厘米;
长方形的长为4厘米,宽为3厘米;
(2)在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数;据此解答。
【详解】
①摆成长是( 12 )厘米,宽是( 1 )厘米的长方形,即( 12 )×( 1 )=12。
②摆成长是( 6 )厘米,宽是( 2 )厘米的长方形,即( 6 )×( 2 )=12。
……
以上所填的数都是12的( 因 )数,12是这些数的( 倍 )数。
所以就得到:如果a×b=c (a、b、c是不为0的整数),那么,c是( a )和( b )的倍数,a和b是c的( 因 )。
【点睛】
掌握因数和倍数的意义是解答题目的关键。
10.√
【解析】
【分析】
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
【详解】
1是所有非零自然数的因数,说法正确。
故答案为:√
【点睛】
只在自然数(零除外)范围内研究倍数和因数。如果a×b=c(a、b、c都是非0的自然数)那么a和b就是c的因数,c就是a和b的倍数。
11.×
【解析】
【分析】
只在自然数(零除外)范围内研究倍数和因数。如果a×b=c(a、b、c都是非0的自然数)那么a和b就是c的因数,c就是a和b的倍数。
【详解】
4×7=28,28是4和7的倍数,4和7是28的因数,所以原题说法错误。
【点睛】
因数和倍数两个不同的概念是相互依存的,不能单独存在。
12.×
【解析】
【分析】
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数;据此解答。
【详解】
0.5是小数不是整数,所以4是0.5的倍数这种说法不正确。
故答案为:×
【点睛】
掌握因数和倍数的意义是解答题目的关键。
13.×
【解析】
【分析】
一个数的最大因数是它本身,一个数的最小倍数也是它本身,据此解答即可。
【详解】
一个数的因数有可能和它的倍数相等,原题说法错误;
故答案为:×。
【点睛】
明确一个数因数与倍数的特点是解答本题的关键。
14.√
【解析】
【分析】
在乘数和积都是整数的乘法算式中,积是乘数的倍数,乘数是积的因数,由此解答即可。
【详解】
因为78=56,所以56是7和8的倍数,7和8是56的因数,原题说法正确;
故答案为:√。
【点睛】
本题较易,考查了因数和倍数的知识点。
15.他说的对。验证过程见详解。
【解析】
【分析】
如果一个自然数等于它的全部因数(不包括本身)的和,这样的数叫“完美数”。依照“完美数”的概念,可先列举出28的所有因数,并通过求和的方法来验证。
【详解】
他说的对。因为28的因数有:1、2、4、7、14、28,这几个因数的关系是:1+2+4+7+14=28。所以28是完全数。
【点睛】
通过题目举例,能够初步理解“完全数”的含义,其中的易错点在于相加的因数不包括这个数本身。本题很好的训练了学生们缜密思考的能力。
16.48名
【解析】
【分析】
4人一组或6人一组都正好分完,说明该班的人数即是4的倍数又是6的倍数,且是40多人,则找到符合条件的人数即可。
【详解】
4的倍数有:4、8、12、16、20、40、48……
6的倍数有:6、12、24、36、42、48……
则符合条件是48。
答:五(1)班有48名同学。
【点睛】
本题考查求两个数的公倍数,明确该班人数在40几人是范围是解题的关键。
17.排3行,每行16人;排4行,每行12人;排6行,每行8人
【解析】
【分析】
根据题意可知,就是找48的因数,根据求一个数的因数的方法,直接列举即可。
【详解】
48的因数有:1、2、3、4、6、8、12、16、24、48;
因为每行或每列的人数不得少于3人,所以可以排3行,每行16人、也可以排4行,每行12人、也可以排6行,每行8人。
【点睛】
解答本题的关键是将问题转化为求48的因数,根据找因数的方法将48的因数一一列举出来,再根据题目中的其他信息进一步解答即可。
18.72个
【解析】
【分析】
根据题意可知,苹果的个数应该是4和6的公倍数,据此先求出4和6的最小公倍数,进而求得最小公倍数的倍数(此数必须是大于70并且小于80的数)
【详解】
4和6的最小公倍数是12,
因为12×6=72,72符合题意,
所以有72个苹果。
答:共买了72个苹果。
【点睛】
本题考查求两个数的公倍数再结合题意求出答案,明确题中苹果的个数的范围是解题的关键。
19.(1)每组最多有6人
(2)答:最少花7分钟才能通知到每个人。
【解析】
【分析】
(1)由题意知:要使两个年级每个小组的人数相同并每组人数最多、这个数值既是48的最大约数,也是54的最大约数。
(2)老师首先用1分钟通知第一个队员,第二分钟由老师和1个队员两人分别通知1个队员,现在通知的一共1+2=3个队员,第三分钟可以推出通知的一共3 +4= 7个队员,以此类推,第四分钟通知的一共7 +8= 15个队员,第五分钟最多可通知到15 + 16= 31个队员,
第六分钟最多可通知到31 + 32 = 63个队员, ……由此问题解决.
【详解】
(1)48的约数有:1、2、3、4、6、8、12、16、24、48
54的约数有:1、2、3、6、9、18、27、54
48和54的最大公约数是:6
答:每组最多有6人。
(2)第一分钟通知到1个队员;
第二分钟最多可通知到3个队员;
第三分钟最多可通知到7个队员;
第四分钟最多可通知到15个队员;
第五分钟最多可通知到31个队员;
第六分钟最多可通知到63个队员;
第7分钟最多可通知到127个队员;
127>48+54
所以最少需要7分钟.
答:最少花7分钟才能通知到每个人。
【点睛】
在“打电话”的优化问题中:“相互通知” 这种方法最省时,所以它是最优方案;规律是:新接到通知的人数等于前一分钟通知到的师生的总人数,新接到通知的队员数是总人数的一半;本题还可以通过画示意图和列表找打电话最优方案的规律。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.24的因数有( )个。
A.8 B.12 C.无数
2.一个数,它既是6的倍数,又是6的因数,这个数是( )。
A.1 B.6 C.12
3.15的因数有( )个,倍数有( )个。
A.3;无数 B.4;无数 C.无数;5 D.无数;无数
4.一个数有因数3,又是4的倍数,这个数可能是( )。
A.18 B.24 C.32
5.根据。下列叙述正确的是( )。
A.36是倍数 B.4是因数
C.36是4的倍数 D.以上叙述均正确
二、填空题
6.15的所有因数有( ),50以内是15的倍数有( )。
7.72÷8=9,所以( )和( )是( )的因数,( )是( )和( )倍数。
8.在圈内写上合适的数。
9.用12个边长是1cm的小正方形摆一个长方形,你会几种摆法?
①摆成长是( )厘米,宽是( )厘米的长方形,即( )×( )=12。
②摆成长是( )厘米,宽是( )厘米的长方形,即( )×( )=12。
……
以上所填的数都是12的( )数,12是这些数的( )数。
所以就得到:如果a×b=c (a、b、c是不为0的整数),那么,c是( )和( )的倍数,a和b是c的( )。
三、判断题
10.1是所有非零自然数的因数。( )
11.4×7=28,28是倍数,4和7是因数。( )
12.4是0.5的倍数。( )
13.一个数的因数总比它的倍数小。( )
14.因为78=56,所以56是7和8的倍数,7和8是56的因数。( )
四、解答题
15.6的因数有1、2、3、6,这几个因数的关系是:1+2+3=6。像6这样的数,叫做完全数(也叫完美数)。小明说:28也是完全数。他说的对吗?请写出你的验证过程。
16.五(1)班有多少名同学?
17.体操表演队由48名同学组成,表演时要排成长方形队形,都可以怎样排?(至少写出3种排法)
18.李奶奶过生日时买来了70多个苹果。如果每盘装4个,正好装完;如果每盘装6个,也正好装完。
19.学校组建合唱团,五年级有48人报名,六年级有54人报名。老师准备把两个年级的同学分别分成若干小组进行训练。
(1)要使两个年级每个小组的人数相同,每组最多有多少人?
(2)暑假期间有一个紧急演出,老师需要尽快通知到每一个队员。如果采用打电话的方式,每分钟通知1人,最少要花( )分钟才能通知到每个人。(直接填出答案即可)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
找因数,从最小的自然数1找起,一直找到它本身,一对对找。
【详解】
24的因数有:1、2、3、4、6、8、12、24,共8个。
故答案为:A
【点睛】
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
2.B
【解析】
【分析】
一个数只有本身既是自己的因数,也是自己的倍数。据此解题。
【详解】
一个数,它既是6的倍数,又是6的因数,这个数是6。
故答案为:B
【点睛】
本题考查了因数和倍数,掌握因数和倍数的特征和求法是解题的关键。
3.B
【解析】
【分析】
找一个数的因数,可以一对一对的找,把15写成两个数的乘积,那么每一个乘积中的因数都是15的因数,然后从小到大依次写出即可;
15的倍数,15乘1、2、3……;有无数个。
【详解】
15的因数有1,3,5,15(4)个,倍数有(无数)个。
故答案选:B。
【点睛】
理解掌握找一个数的因数、倍数的方法是关键。
4.B
【解析】
【分析】
分别看看每个选项中的数是否符合有因数3,又是4的倍数即可。
【详解】
A.18有因数3,但不是4的倍数;
B.24既有因数3,又是4的倍数;
C.32是4的倍数,但没有因数3;
故答案为:B。
【点睛】
本题较易,熟练掌握求一个数的因数与倍数的方法是解答本题的关键。
5.C
【解析】
【分析】
如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;据此选择即可。
【详解】
根据,我们可以说36是4和9的倍数,4和9是36的因数;不能说36是倍数,4和9是因数。
故答案为:C
【点睛】
解答此题要明确:因数和倍数是相互依存的,不能单独存在。
6. 1、3、5、15 15、30、45
【解析】
【分析】
找一个数的因数,可以一对一对的找,把15写成两个数的乘积,那么每一个乘积中的因数都是20的因数,然后从小到大依次写出即可;
15的倍数,15乘1、2、3……;
【详解】
15的所有因数有1、3、5、15,50以内是15的倍数有15、30、45。
【点睛】
解答此题应根据找一个数因数和倍数的方法进行解答。
7. 8 9 72 72 8 9
【解析】
【分析】
根据因数和倍数的意义,当a÷b=c(a、b、c为非0自然数)我们说a是b和c的倍数,b和c是a的因数。据此解答。
【详解】
72÷8=9,所以(8)和(9)是(72)的因数,(72)是(8)和(9)倍数。
【点睛】
掌握因数和倍数的意义是解题的关键。
8.见详解
【解析】
【分析】
60的因数从1开始依次计算,就能一对一对的找出来;6的倍数有无数个。
【详解】
【点睛】
一个数的因数是有限个,从小到大依次列出就能不重不漏;一个数的倍数有无数个。
9. 12 1 12 1 6 2 6 2 因 倍 a b 因
【解析】
【分析】
(1)长方形的长为12厘米,宽为1厘米;
长方形的长为6厘米,宽为2厘米;
长方形的长为4厘米,宽为3厘米;
(2)在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数;据此解答。
【详解】
①摆成长是( 12 )厘米,宽是( 1 )厘米的长方形,即( 12 )×( 1 )=12。
②摆成长是( 6 )厘米,宽是( 2 )厘米的长方形,即( 6 )×( 2 )=12。
……
以上所填的数都是12的( 因 )数,12是这些数的( 倍 )数。
所以就得到:如果a×b=c (a、b、c是不为0的整数),那么,c是( a )和( b )的倍数,a和b是c的( 因 )。
【点睛】
掌握因数和倍数的意义是解答题目的关键。
10.√
【解析】
【分析】
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
【详解】
1是所有非零自然数的因数,说法正确。
故答案为:√
【点睛】
只在自然数(零除外)范围内研究倍数和因数。如果a×b=c(a、b、c都是非0的自然数)那么a和b就是c的因数,c就是a和b的倍数。
11.×
【解析】
【分析】
只在自然数(零除外)范围内研究倍数和因数。如果a×b=c(a、b、c都是非0的自然数)那么a和b就是c的因数,c就是a和b的倍数。
【详解】
4×7=28,28是4和7的倍数,4和7是28的因数,所以原题说法错误。
【点睛】
因数和倍数两个不同的概念是相互依存的,不能单独存在。
12.×
【解析】
【分析】
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数;据此解答。
【详解】
0.5是小数不是整数,所以4是0.5的倍数这种说法不正确。
故答案为:×
【点睛】
掌握因数和倍数的意义是解答题目的关键。
13.×
【解析】
【分析】
一个数的最大因数是它本身,一个数的最小倍数也是它本身,据此解答即可。
【详解】
一个数的因数有可能和它的倍数相等,原题说法错误;
故答案为:×。
【点睛】
明确一个数因数与倍数的特点是解答本题的关键。
14.√
【解析】
【分析】
在乘数和积都是整数的乘法算式中,积是乘数的倍数,乘数是积的因数,由此解答即可。
【详解】
因为78=56,所以56是7和8的倍数,7和8是56的因数,原题说法正确;
故答案为:√。
【点睛】
本题较易,考查了因数和倍数的知识点。
15.他说的对。验证过程见详解。
【解析】
【分析】
如果一个自然数等于它的全部因数(不包括本身)的和,这样的数叫“完美数”。依照“完美数”的概念,可先列举出28的所有因数,并通过求和的方法来验证。
【详解】
他说的对。因为28的因数有:1、2、4、7、14、28,这几个因数的关系是:1+2+4+7+14=28。所以28是完全数。
【点睛】
通过题目举例,能够初步理解“完全数”的含义,其中的易错点在于相加的因数不包括这个数本身。本题很好的训练了学生们缜密思考的能力。
16.48名
【解析】
【分析】
4人一组或6人一组都正好分完,说明该班的人数即是4的倍数又是6的倍数,且是40多人,则找到符合条件的人数即可。
【详解】
4的倍数有:4、8、12、16、20、40、48……
6的倍数有:6、12、24、36、42、48……
则符合条件是48。
答:五(1)班有48名同学。
【点睛】
本题考查求两个数的公倍数,明确该班人数在40几人是范围是解题的关键。
17.排3行,每行16人;排4行,每行12人;排6行,每行8人
【解析】
【分析】
根据题意可知,就是找48的因数,根据求一个数的因数的方法,直接列举即可。
【详解】
48的因数有:1、2、3、4、6、8、12、16、24、48;
因为每行或每列的人数不得少于3人,所以可以排3行,每行16人、也可以排4行,每行12人、也可以排6行,每行8人。
【点睛】
解答本题的关键是将问题转化为求48的因数,根据找因数的方法将48的因数一一列举出来,再根据题目中的其他信息进一步解答即可。
18.72个
【解析】
【分析】
根据题意可知,苹果的个数应该是4和6的公倍数,据此先求出4和6的最小公倍数,进而求得最小公倍数的倍数(此数必须是大于70并且小于80的数)
【详解】
4和6的最小公倍数是12,
因为12×6=72,72符合题意,
所以有72个苹果。
答:共买了72个苹果。
【点睛】
本题考查求两个数的公倍数再结合题意求出答案,明确题中苹果的个数的范围是解题的关键。
19.(1)每组最多有6人
(2)答:最少花7分钟才能通知到每个人。
【解析】
【分析】
(1)由题意知:要使两个年级每个小组的人数相同并每组人数最多、这个数值既是48的最大约数,也是54的最大约数。
(2)老师首先用1分钟通知第一个队员,第二分钟由老师和1个队员两人分别通知1个队员,现在通知的一共1+2=3个队员,第三分钟可以推出通知的一共3 +4= 7个队员,以此类推,第四分钟通知的一共7 +8= 15个队员,第五分钟最多可通知到15 + 16= 31个队员,
第六分钟最多可通知到31 + 32 = 63个队员, ……由此问题解决.
【详解】
(1)48的约数有:1、2、3、4、6、8、12、16、24、48
54的约数有:1、2、3、6、9、18、27、54
48和54的最大公约数是:6
答:每组最多有6人。
(2)第一分钟通知到1个队员;
第二分钟最多可通知到3个队员;
第三分钟最多可通知到7个队员;
第四分钟最多可通知到15个队员;
第五分钟最多可通知到31个队员;
第六分钟最多可通知到63个队员;
第7分钟最多可通知到127个队员;
127>48+54
所以最少需要7分钟.
答:最少花7分钟才能通知到每个人。
【点睛】
在“打电话”的优化问题中:“相互通知” 这种方法最省时,所以它是最优方案;规律是:新接到通知的人数等于前一分钟通知到的师生的总人数,新接到通知的队员数是总人数的一半;本题还可以通过画示意图和列表找打电话最优方案的规律。
答案第1页,共2页
答案第1页,共2页
