小学数学苏教版六年级下册 第六单元正比例和反比例单元测试(带答案)
文档属性
| 名称 | 小学数学苏教版六年级下册 第六单元正比例和反比例单元测试(带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 391.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 17:59:16 | ||
图片预览


文档简介
2021-2022学年度苏教版六年级数学下册第六单元综合测试卷(含答案)
一、用心推敲,公正判断。(共5题;共5分)
1.圆的周长和它的直径成正比例。( )
2.一根电线,用去的长度与剩下的长度成反比例。( )
3.订阅《少年文艺》的份数与总钱数成反比例.( )
4.长方体的底面积一定,高和体积成反比例.( )
5.3m-2n=0,m和n成正比例。( )
二、精挑细选,择优录取。(共7题;共14分)
6.下面式子表示x和y成正比例的式子是( )。
A.x+y=12 B.x-y=12 C.xy=12 D.x:y=12
7.今年妈妈的年龄是儿子的3倍,儿子的年龄和妈妈的年龄( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
8.在C=πd中,如果C一定,那么π和d( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
9.( )中的两种量不成比例。
A.从北京到广州,列车行驶的平均速度和所需时间
B.一箱苹果,吃去的个数和剩下的个数
C.同一时刻,同一地点,物体的高度和影子的长度
D.同一个文件,平均下载速度和下载时间
10.下列算式中,a和b成正比例的是( )。
A.c÷a=b(c一定,a不等于0)
B.a×b=c(c一定,a、b均不等于0)
C.a÷b=c(c一定,b不等于0)
D.c÷b=a(c一定,b不等于0)
11.假如b=k×a,b是一定的,a、b、k均不为0,下列说法正确的是( )。
A.a和k成正比例关系 B.k和a成反比例关系
C.a和k不成比例 D.无法判断
12.如果用x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用式子表示为( )。
A.x×y=k(一定) B. =k(一定)
C.x×k=y(k一定) D.k×y=x(k一定)
三、细心读题,谨慎填写。(共5题;共19分)
13.用同样的砖铺地,铺地面积和用砖块数如下表:
铺地面积/平方米 1 2 3 4 5
用砖块数 4 8 12 16 20
(1)表中 和 是相关联的量, 随着 的变化而变化。
(2)表中用砖块数和铺地面积这两种量相对应的两个数的比的比值是 ,这个比值所表示的意义是 。
(3)因为用砖块数和铺地面积的 是一定的,所以铺地面积和用砖块数成 比例。
14.比例尺一定,图上距离和实际距离成 比例。图上距离一定,实际距离和比例尺成 比例。实际距离一定,图上距离和比例尺成 比例。
15.下表中,如果a和b成正比例,则空缺处填 ;如果a和b成反比例,则空缺处填 。
a 8 6
b 12
16.4:a=3:b,a和b成 比例。 =4y,x和y成 比例。
17.下面的图像表示了小明爸爸骑车行驶的路程和时间的关系。
(1)图中反映了 和 成 比例。
(2)由图像判断,骑车40千米需要 分钟,骑车50分钟可行 千米。
四、慎重审题,巧思妙算。(共2题;共14分)
18.口算。
475-298= 1-0.09= 0.22= 1÷ × = ÷3+ × =
3.3+7= 16÷0.8= - = 4×4÷ = ( + )×24=
19.解方程。
(1) : =x:
(2)3x- x=
(3)x-7.9+2.1=3.9
五、走进生活,解决问题。(共5题;共48分)
20.一辆小汽车以平均每小时90千米的速度行驶。
(1)填写下表。
时间/时 1 2 4 6 9 …
路程/千米 90 180
(2)根据表中的数据,在下图中描出行驶的时间与路程的对应点,再把这些点按顺序连接。
小汽车行驶的时间和路程成( )比例,理由是( )。
(3)根据图像估计行300千米大约要 小时。2.5小时大约行 千米。
21.仔细观察,补全下表并回答下列问题。
x 6 18 24 75 90 231
y 2 6 10 77 120
(1)仔细观察,补全表格。
(2)观察表格,y与x这两个量的 一定,x和y成 比例。
(3)如果x=2.4,那么y= ,如果y= ,x= 。
22.学校食堂有一批大米。
(1)把下表填写完整。
每天的用量/千克 50 40
所用的天数 10 20 40 50 80
(2)相对应的每天的用量和所用的天数的积各是多少?
(3)这个乘积表示的实际意义是什么?你能用式子表示它与每天的用量和所用的天数之间的关系吗?
(4)每天的用量和所用的天数两个量成反比例关系吗?为什么?
(5)如果每天吃125千克大米,那么这批大米够吃几天?
23.
(1)如果x和y成正比例,并且 =20,请完成下表。
y 20 80 130 1000 850
x 1.5 8 0.4 10
(2)在下图中,描出(1)中y与x所对应的点(注意找出几个关键点),然后连成线。
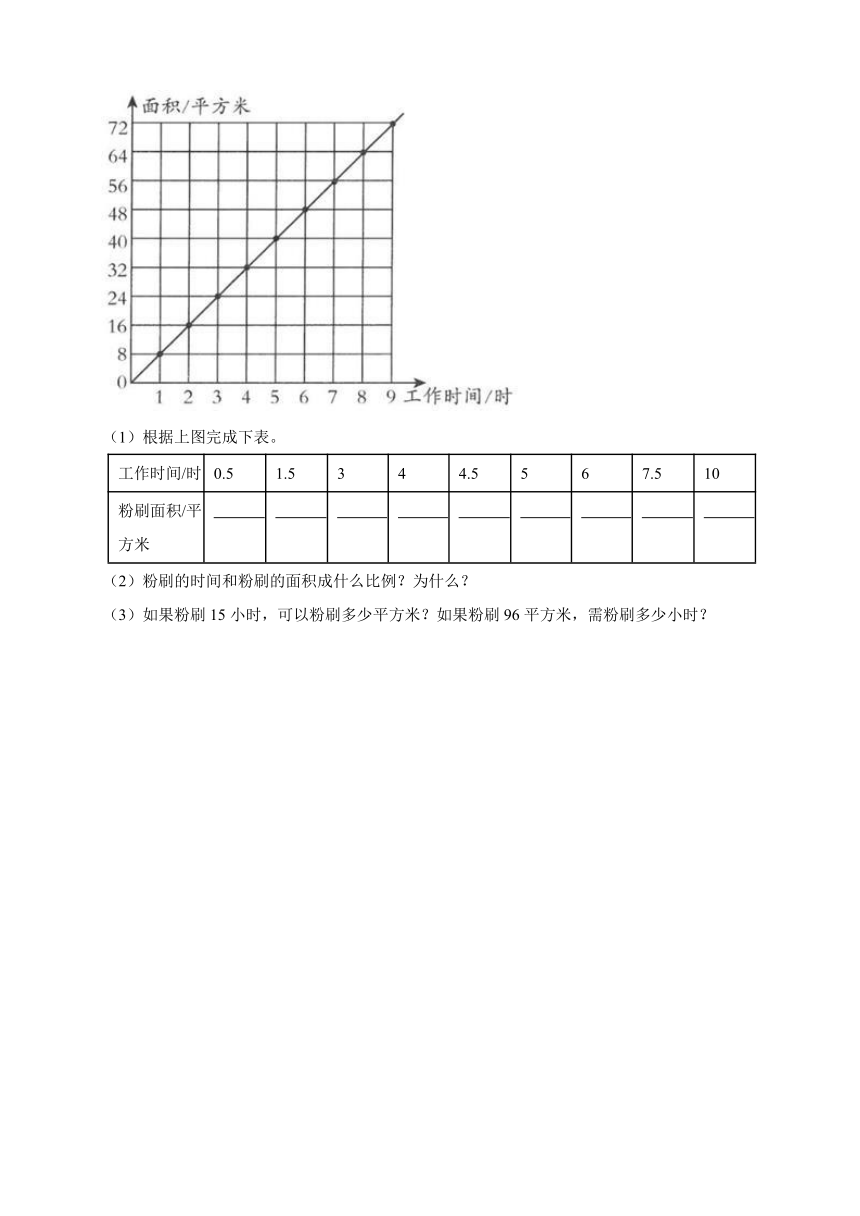
24.小明帮助爸爸粉刷墙壁,他粉刷的时间和面积的情况如图所示。
(1)根据上图完成下表。
工作时间/时 0.5 1.5 3 4 4.5 5 6 7.5 10
粉刷面积/平方米
(2)粉刷的时间和粉刷的面积成什么比例?为什么?
(3)如果粉刷15小时,可以粉刷多少平方米?如果粉刷96平方米,需粉刷多少小时?
答案解析部分
1.(1)正
2.(1)错误
3.(1)错误
4.(1)错误
5.(1)正
6.D
7.C
8.C
9.B
10.C
11.B
12.A
13.(1)用砖块数;铺地面积;用砖块数;铺地面积
(2)4;每平方米用砖的块数
(3)比的比值;正
14.正;反;正
15.9;16
16.正;反
17.(1)路程;时间;正
(2)200;10
18.475-298=177 1-0.09=0.91 0.22=0.04 1÷ × = ÷3+ × =
3.3+7=10.3 16÷0.8=20 - = 4×4÷ =9 ( + )×24=14
19.(1) :=x:
解:x=×
x=
x÷=÷
x=
(2) 3x-x=
解:x=
x÷=÷
x=
(3) x-7.9+2.1=3.9
解:x-5.8=3.9
x-5.8+5.8=3.9+5.8
x=9.7
20.(1)360;540;810
(2)
小汽车行驶的时间和路程成正比例,理由是小汽车行驶的路程与时间的比的比值一定。
(3)3.3;225(答案不唯一)
21.(1) x
6
18
24
30
75
90
231
360
y
2
6
8
10
25 30
77
120
(2)比的比值;正
(3)0.8;2
22.(1) 每天的用量/千克100
50
40
25 20 12.5
所用的天数
10
20
25
40
50
80
(2)100×10=1000(千克),50×20=1000(千克),
40×25=1000(千克),25×40=1000(千克),
20×50=1000(千克),12.5×80=1000(千克)。
答:相对应的每天的用量和所用的天数的积均为1000千克。
(3)这个乘积表示这批大米的总量。
每天的用量×所用的天数=这批大米的总量(一定)。
(4)每天的用量和所用的天数两个量成反比例关系,因为每天的用量和所用的天数的乘积一定。
(5)1000÷125=8(天)
答:这批大米够吃8天。
23.(1) y
20
30
80
160
130
8 200
1000
850
x
1
1.5
4
8
6.5
0.4
10
50 42.5
(2)
24.(1)4;12;24;32;36;40;48;60;80
(2)粉刷的时间和粉刷的面积成正比例,因为粉刷的面积和粉刷的时间的比的比值一定。
(3)解:
24÷3=8(平方米)
8×15=120(平方米)
96÷8=12(小时)
答:如果粉刷15小时,可以粉刷120平方米;如果粉刷96平方米,需粉刷12小时。
一、用心推敲,公正判断。(共5题;共5分)
1.圆的周长和它的直径成正比例。( )
2.一根电线,用去的长度与剩下的长度成反比例。( )
3.订阅《少年文艺》的份数与总钱数成反比例.( )
4.长方体的底面积一定,高和体积成反比例.( )
5.3m-2n=0,m和n成正比例。( )
二、精挑细选,择优录取。(共7题;共14分)
6.下面式子表示x和y成正比例的式子是( )。
A.x+y=12 B.x-y=12 C.xy=12 D.x:y=12
7.今年妈妈的年龄是儿子的3倍,儿子的年龄和妈妈的年龄( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
8.在C=πd中,如果C一定,那么π和d( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
9.( )中的两种量不成比例。
A.从北京到广州,列车行驶的平均速度和所需时间
B.一箱苹果,吃去的个数和剩下的个数
C.同一时刻,同一地点,物体的高度和影子的长度
D.同一个文件,平均下载速度和下载时间
10.下列算式中,a和b成正比例的是( )。
A.c÷a=b(c一定,a不等于0)
B.a×b=c(c一定,a、b均不等于0)
C.a÷b=c(c一定,b不等于0)
D.c÷b=a(c一定,b不等于0)
11.假如b=k×a,b是一定的,a、b、k均不为0,下列说法正确的是( )。
A.a和k成正比例关系 B.k和a成反比例关系
C.a和k不成比例 D.无法判断
12.如果用x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用式子表示为( )。
A.x×y=k(一定) B. =k(一定)
C.x×k=y(k一定) D.k×y=x(k一定)
三、细心读题,谨慎填写。(共5题;共19分)
13.用同样的砖铺地,铺地面积和用砖块数如下表:
铺地面积/平方米 1 2 3 4 5
用砖块数 4 8 12 16 20
(1)表中 和 是相关联的量, 随着 的变化而变化。
(2)表中用砖块数和铺地面积这两种量相对应的两个数的比的比值是 ,这个比值所表示的意义是 。
(3)因为用砖块数和铺地面积的 是一定的,所以铺地面积和用砖块数成 比例。
14.比例尺一定,图上距离和实际距离成 比例。图上距离一定,实际距离和比例尺成 比例。实际距离一定,图上距离和比例尺成 比例。
15.下表中,如果a和b成正比例,则空缺处填 ;如果a和b成反比例,则空缺处填 。
a 8 6
b 12
16.4:a=3:b,a和b成 比例。 =4y,x和y成 比例。
17.下面的图像表示了小明爸爸骑车行驶的路程和时间的关系。
(1)图中反映了 和 成 比例。
(2)由图像判断,骑车40千米需要 分钟,骑车50分钟可行 千米。
四、慎重审题,巧思妙算。(共2题;共14分)
18.口算。
475-298= 1-0.09= 0.22= 1÷ × = ÷3+ × =
3.3+7= 16÷0.8= - = 4×4÷ = ( + )×24=
19.解方程。
(1) : =x:
(2)3x- x=
(3)x-7.9+2.1=3.9
五、走进生活,解决问题。(共5题;共48分)
20.一辆小汽车以平均每小时90千米的速度行驶。
(1)填写下表。
时间/时 1 2 4 6 9 …
路程/千米 90 180
(2)根据表中的数据,在下图中描出行驶的时间与路程的对应点,再把这些点按顺序连接。
小汽车行驶的时间和路程成( )比例,理由是( )。
(3)根据图像估计行300千米大约要 小时。2.5小时大约行 千米。
21.仔细观察,补全下表并回答下列问题。
x 6 18 24 75 90 231
y 2 6 10 77 120
(1)仔细观察,补全表格。
(2)观察表格,y与x这两个量的 一定,x和y成 比例。
(3)如果x=2.4,那么y= ,如果y= ,x= 。
22.学校食堂有一批大米。
(1)把下表填写完整。
每天的用量/千克 50 40
所用的天数 10 20 40 50 80
(2)相对应的每天的用量和所用的天数的积各是多少?
(3)这个乘积表示的实际意义是什么?你能用式子表示它与每天的用量和所用的天数之间的关系吗?
(4)每天的用量和所用的天数两个量成反比例关系吗?为什么?
(5)如果每天吃125千克大米,那么这批大米够吃几天?
23.
(1)如果x和y成正比例,并且 =20,请完成下表。
y 20 80 130 1000 850
x 1.5 8 0.4 10
(2)在下图中,描出(1)中y与x所对应的点(注意找出几个关键点),然后连成线。
24.小明帮助爸爸粉刷墙壁,他粉刷的时间和面积的情况如图所示。
(1)根据上图完成下表。
工作时间/时 0.5 1.5 3 4 4.5 5 6 7.5 10
粉刷面积/平方米
(2)粉刷的时间和粉刷的面积成什么比例?为什么?
(3)如果粉刷15小时,可以粉刷多少平方米?如果粉刷96平方米,需粉刷多少小时?
答案解析部分
1.(1)正
2.(1)错误
3.(1)错误
4.(1)错误
5.(1)正
6.D
7.C
8.C
9.B
10.C
11.B
12.A
13.(1)用砖块数;铺地面积;用砖块数;铺地面积
(2)4;每平方米用砖的块数
(3)比的比值;正
14.正;反;正
15.9;16
16.正;反
17.(1)路程;时间;正
(2)200;10
18.475-298=177 1-0.09=0.91 0.22=0.04 1÷ × = ÷3+ × =
3.3+7=10.3 16÷0.8=20 - = 4×4÷ =9 ( + )×24=14
19.(1) :=x:
解:x=×
x=
x÷=÷
x=
(2) 3x-x=
解:x=
x÷=÷
x=
(3) x-7.9+2.1=3.9
解:x-5.8=3.9
x-5.8+5.8=3.9+5.8
x=9.7
20.(1)360;540;810
(2)
小汽车行驶的时间和路程成正比例,理由是小汽车行驶的路程与时间的比的比值一定。
(3)3.3;225(答案不唯一)
21.(1) x
6
18
24
30
75
90
231
360
y
2
6
8
10
25 30
77
120
(2)比的比值;正
(3)0.8;2
22.(1) 每天的用量/千克100
50
40
25 20 12.5
所用的天数
10
20
25
40
50
80
(2)100×10=1000(千克),50×20=1000(千克),
40×25=1000(千克),25×40=1000(千克),
20×50=1000(千克),12.5×80=1000(千克)。
答:相对应的每天的用量和所用的天数的积均为1000千克。
(3)这个乘积表示这批大米的总量。
每天的用量×所用的天数=这批大米的总量(一定)。
(4)每天的用量和所用的天数两个量成反比例关系,因为每天的用量和所用的天数的乘积一定。
(5)1000÷125=8(天)
答:这批大米够吃8天。
23.(1) y
20
30
80
160
130
8 200
1000
850
x
1
1.5
4
8
6.5
0.4
10
50 42.5
(2)
24.(1)4;12;24;32;36;40;48;60;80
(2)粉刷的时间和粉刷的面积成正比例,因为粉刷的面积和粉刷的时间的比的比值一定。
(3)解:
24÷3=8(平方米)
8×15=120(平方米)
96÷8=12(小时)
答:如果粉刷15小时,可以粉刷120平方米;如果粉刷96平方米,需粉刷12小时。
