初中数学苏科版八年级下册 9.3平行四边形(第2课时) 课件(共17张)
文档属性
| 名称 | 初中数学苏科版八年级下册 9.3平行四边形(第2课时) 课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 354.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
§9.3 平行四边形(2)
温习旧知
如图, 已知点A, B, C分别在△DEF的各边上, AB//DE,
BC//EF, CA//FD.
求证:点A, B, C 分别是△DEF各边的中点.
定义:两组对边分别平行的四边形是平行四边形.
性质:
平行四边形的对边平行、对边相等、对角相等、对角线互相平分.
新知探究
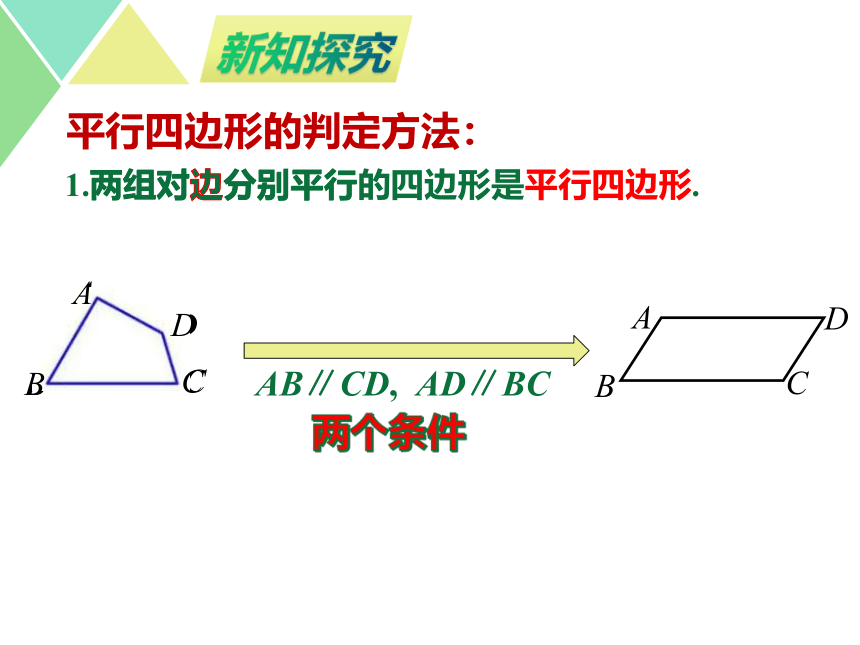
1.两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法:
A
B
C
D
A
B
C
D
A
B
C
D
两组对边分别平行
AB∥CD, AD∥BC
两个条件
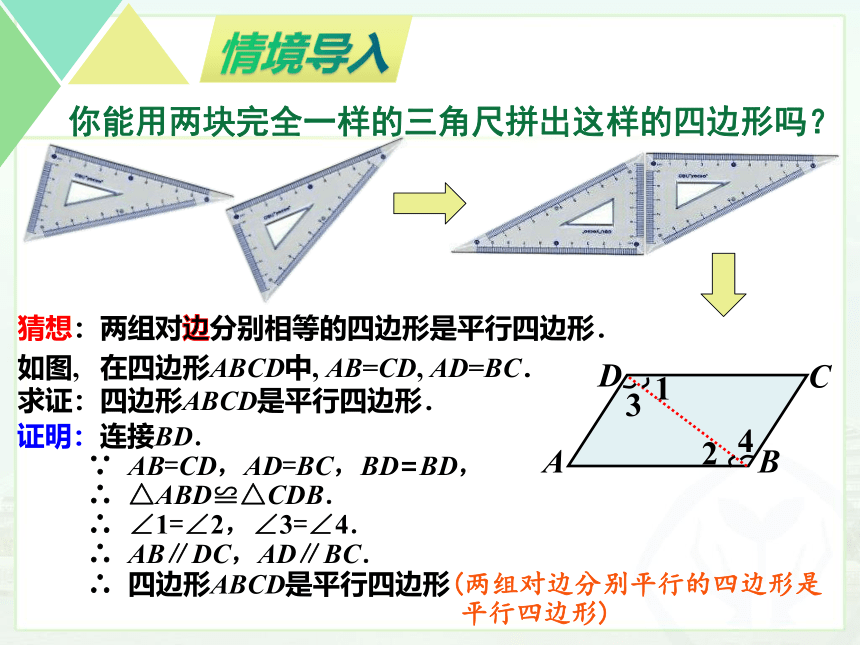
你能用两块完全一样的三角尺拼出这样的四边形吗?
情境导入
D
A
B
C
猜想:两组对边分别相等的四边形是平行四边形.
如图, 在四边形ABCD中, AB=CD, AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接BD.
∵ AB=CD,AD=BC,BD=BD,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形(两组对边分别平行的四边形是
平行四边形)
1
2
3
4
新知探究
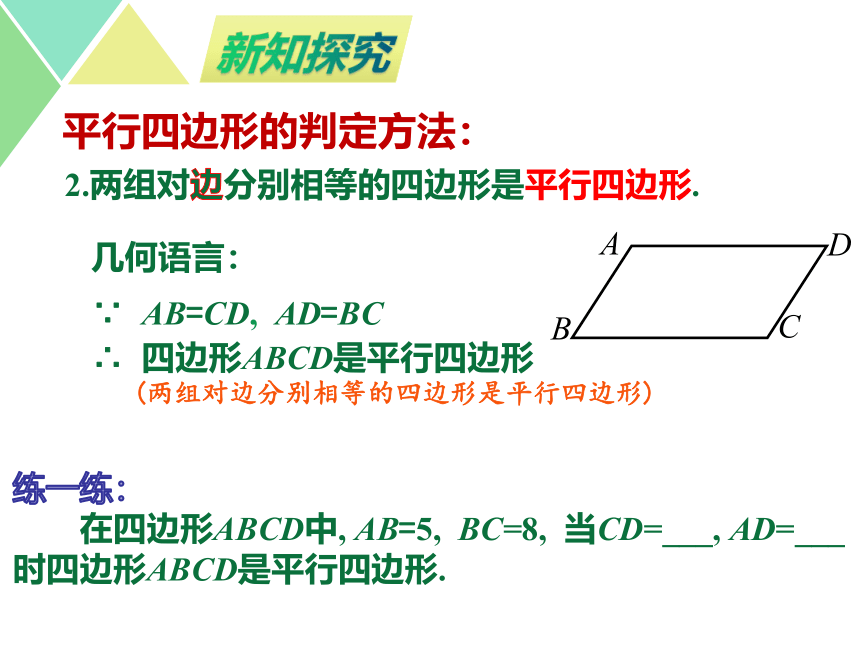
2.两组对边分别相等的四边形是平行四边形.
平行四边形的判定方法:
A
B
C
D
几何语言:
∵ AB=CD, AD=BC
∴ 四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
练一练:
在四边形ABCD中, AB=5, BC=8, 当CD=___, AD=___时四边形ABCD是平行四边形.
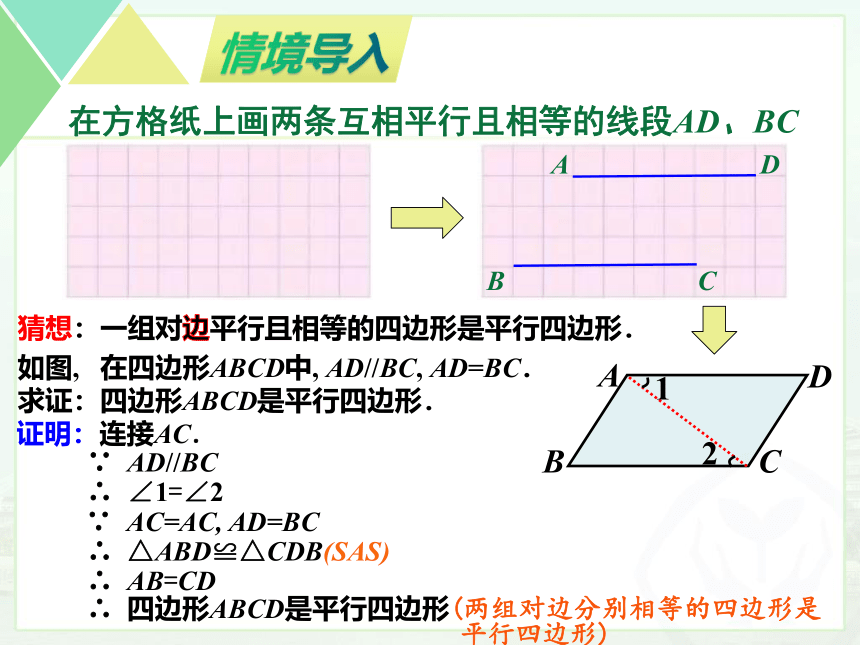
在方格纸上画两条互相平行且相等的线段AD、BC
情境导入
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
如图, 在四边形ABCD中, AD//BC, AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵ AD//BC
∴ ∠1=∠2
∵ AC=AC, AD=BC
∴ △ABD≌△CDB(SAS)
∴ AB=CD
∴ 四边形ABCD是平行四边形(两组对边分别相等的四边形是
平行四边形)
1
2
A D
B C
新知探究
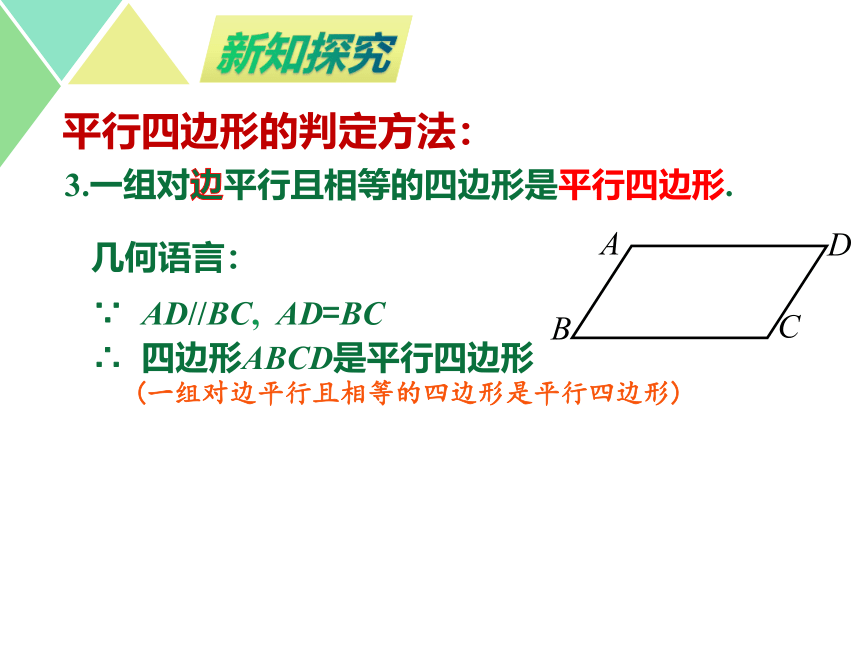
3.一组对边平行且相等的四边形是平行四边形.
平行四边形的判定方法:
A
B
C
D
几何语言:
∵ AD//BC, AD=BC
∴ 四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
新知概括
A
B
C
D
A
B
C
D
四边形ABCD ABCD
1.两组对边分别平行
2.两组对边分别相等
3.一组对边平行且相等
平行四边形的判定方法:
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AB=CD
两个条件
习题巩固
1.如图, 在四边形ABCD中, AB//CD,
要使四边形ABCD是平行四边形,
下列可添加的条件中, 不正确的
是( )
A. AB=CD
B. AD//BC
C. ∠A=∠C
D. AD=BC
D
变式1:
下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行, 另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行, 一组对角相等的四边形是平行四边形
B
习题巩固
1.如图, 在四边形ABCD中, AB//CD,
要使四边形ABCD是平行四边形,
下列可添加的条件中, 不正确的
是( )
A. AB=CD
B. AD//BC
C. ∠A=∠C
D. AD=BC
D
变式2:
在四边形ABCD中, 已知AB//CD,
添加一个条件:_______________,
使得四边形ABCD是平行四边形.
习题巩固
2.如图, 在四边形ABCD中, AD//BC, AD=12cm, BC=15cm,
点P 自点A向D以1cm/s的速度运动, 到D点即停止. 点Q
自点C向B以2cm/s的速度运动, 到B点即停止, 点P, Q同
时出发, 设运动时间为t(s).
(1)用含t的代数式表示:
AP=______, DP=______,
BQ=______, CQ=______;
(2)当t=___时, 四边形APQB是平行四边形?
(3)当t=___时, 四边形PDCQ是平行四边形?
习题巩固
3.如图, 在 ABCD中, 点E、F分别在AD、BC上, 且AE=CF.
求证:四边形BFDE是平行四边形.
习题巩固
3.如图, 在 ABCD中, 点E、F分别在AD、BC上, 且AE=CF.
求证:四边形BFDE是平行四边形.
习题巩固
3.如图, 在 ABCD中, 点E、F分别在AD、BC上, 且AE=CF.
求证:四边形BFDE是平行四边形.
课堂总结
平行四边形的判定方法:
∴ 四边形ABCD是平行四边形
∵ AB∥CD, AD∥BC
∵ AB=CD, AD=BC
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
∴ 四边形ABCD是平行四边形
∵ AB∥CD, AB=CD
∴ 四边形ABCD是平行四边形
A
B
C
D
类比观察拼图实验
定义
判定定理1
判定定理2
自主完成:
课后检测练习
作业布置
谢谢大家的聆听
§9.3 平行四边形(2)
温习旧知
如图, 已知点A, B, C分别在△DEF的各边上, AB//DE,
BC//EF, CA//FD.
求证:点A, B, C 分别是△DEF各边的中点.
定义:两组对边分别平行的四边形是平行四边形.
性质:
平行四边形的对边平行、对边相等、对角相等、对角线互相平分.
新知探究
1.两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法:
A
B
C
D
A
B
C
D
A
B
C
D
两组对边分别平行
AB∥CD, AD∥BC
两个条件
你能用两块完全一样的三角尺拼出这样的四边形吗?
情境导入
D
A
B
C
猜想:两组对边分别相等的四边形是平行四边形.
如图, 在四边形ABCD中, AB=CD, AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接BD.
∵ AB=CD,AD=BC,BD=BD,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形(两组对边分别平行的四边形是
平行四边形)
1
2
3
4
新知探究
2.两组对边分别相等的四边形是平行四边形.
平行四边形的判定方法:
A
B
C
D
几何语言:
∵ AB=CD, AD=BC
∴ 四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
练一练:
在四边形ABCD中, AB=5, BC=8, 当CD=___, AD=___时四边形ABCD是平行四边形.
在方格纸上画两条互相平行且相等的线段AD、BC
情境导入
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
如图, 在四边形ABCD中, AD//BC, AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵ AD//BC
∴ ∠1=∠2
∵ AC=AC, AD=BC
∴ △ABD≌△CDB(SAS)
∴ AB=CD
∴ 四边形ABCD是平行四边形(两组对边分别相等的四边形是
平行四边形)
1
2
A D
B C
新知探究
3.一组对边平行且相等的四边形是平行四边形.
平行四边形的判定方法:
A
B
C
D
几何语言:
∵ AD//BC, AD=BC
∴ 四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
新知概括
A
B
C
D
A
B
C
D
四边形ABCD ABCD
1.两组对边分别平行
2.两组对边分别相等
3.一组对边平行且相等
平行四边形的判定方法:
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AB=CD
两个条件
习题巩固
1.如图, 在四边形ABCD中, AB//CD,
要使四边形ABCD是平行四边形,
下列可添加的条件中, 不正确的
是( )
A. AB=CD
B. AD//BC
C. ∠A=∠C
D. AD=BC
D
变式1:
下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行, 另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行, 一组对角相等的四边形是平行四边形
B
习题巩固
1.如图, 在四边形ABCD中, AB//CD,
要使四边形ABCD是平行四边形,
下列可添加的条件中, 不正确的
是( )
A. AB=CD
B. AD//BC
C. ∠A=∠C
D. AD=BC
D
变式2:
在四边形ABCD中, 已知AB//CD,
添加一个条件:_______________,
使得四边形ABCD是平行四边形.
习题巩固
2.如图, 在四边形ABCD中, AD//BC, AD=12cm, BC=15cm,
点P 自点A向D以1cm/s的速度运动, 到D点即停止. 点Q
自点C向B以2cm/s的速度运动, 到B点即停止, 点P, Q同
时出发, 设运动时间为t(s).
(1)用含t的代数式表示:
AP=______, DP=______,
BQ=______, CQ=______;
(2)当t=___时, 四边形APQB是平行四边形?
(3)当t=___时, 四边形PDCQ是平行四边形?
习题巩固
3.如图, 在 ABCD中, 点E、F分别在AD、BC上, 且AE=CF.
求证:四边形BFDE是平行四边形.
习题巩固
3.如图, 在 ABCD中, 点E、F分别在AD、BC上, 且AE=CF.
求证:四边形BFDE是平行四边形.
习题巩固
3.如图, 在 ABCD中, 点E、F分别在AD、BC上, 且AE=CF.
求证:四边形BFDE是平行四边形.
课堂总结
平行四边形的判定方法:
∴ 四边形ABCD是平行四边形
∵ AB∥CD, AD∥BC
∵ AB=CD, AD=BC
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
∴ 四边形ABCD是平行四边形
∵ AB∥CD, AB=CD
∴ 四边形ABCD是平行四边形
A
B
C
D
类比观察拼图实验
定义
判定定理1
判定定理2
自主完成:
课后检测练习
作业布置
谢谢大家的聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
