浙江省杭州市萧山区2021-2022学年第二学期九年级开学考试数学试题(word版,含答案)
文档属性
| 名称 | 浙江省杭州市萧山区2021-2022学年第二学期九年级开学考试数学试题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 17:35:40 | ||
图片预览




文档简介
2021学年第二学期九年级期初独立作业 数学试题卷
满分120分 考试时间100分钟
一、选择题(本大题共有10个小题,每小题3分,共30分)
1.抛物线的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
2.若⊙O的半径为5cm,点A到圆心O的距离为4cm,则点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上 C.点A在圆内 D.不能确定
3.九年级(1)班在参加学校4×100m接力赛时,安排了甲、乙、丙、丁四位同学,他们的顺序由抽签随机决定,则甲同学跑第一棒的概率为( )
A.1 B. C. D.
4.若线段AB=2,点P是线段AB的黄金分割点,且APBP,则AP的长为( )
A. B. C. D.
5.如图,是⊙O的直径,点C、D是圆上两点,且∠AOC=,则∠CDB=( )
A. B. C. D.
6.若A(-6, ),B(-3, ),C(1, )为二次函数图象上的三点,则 的大小关系是( )
A. B. C. D.
7.在中,∠C=,AB=4, ,则的长为( )
A.3 B.2 C. D.
8.如图,ΔABC的中线AD,BE交于点F,EG∥BC,交AD于点G,则等于( )
A. 1:2 B. 1:3 C. 2:3 D. 3:5
9.已知二次函数(其中),下列说法正确的是( )
A.当时,都有随着的增大而增大
B.当时,都有随着的增大而减小
C.若时,都有随着的增大而减小,则
D.若时,都有随着的增大而减小,则
10. 如图,半圆O的直径AB=10,弦AC=6,D是的中点,则弦AD的长为( )
A. B.8 C. D.
二、填空题(本大题共有6个小题,每小题4分,共24分)
11.计算=__________.
12.在一个不透明的袋中装有只有颜色不同的10个球,其中6个红色,4个白色,从袋中任意摸出一个球是红球的概率是__________.
13.已知二次函数,函数y与自变量x的部分对应值如下表:
则当y<5时,x的取值范围是__________.
14.如图,在ABCD中,E是AD边上一点,AE:ED=1:2,连结AC,BE交于点F.若,则 = _________.
15.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3,AB=8,则OP长为___________.
16.如图,△ABC内接于半径为的半圆O中,AB为直径,点M是的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,∠ADB=135°且D为BM的中点,则DM的长为___________;BC的长为___________.
三、解答题(本大题共有7小题,共66分)
17.(本题满分6分)
一只不透明的袋子中装有1个红球、2个黄球,这些球除颜色外都相同。小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球。
(1)用画树状图或列表法列出摸出球的所有等可能情况;
(2)求出两次摸出的球都是红色的概率.
18. (本题满分8分)
二次函数的图象经过点(4,3)和(3,0)
(1)求b,c的值;
(2)求出该二次函数图象的顶点坐标和对称轴.
19.(本题满分8分)
如图所示,AB是⊙O的直径,弦AC、BD相交于点E,且C为的中点。若EC=2,tan∠CEB=2.
(1)求证:ΔABE∽ΔDCE,并求出BE的长;
(2)求⊙O的面积.
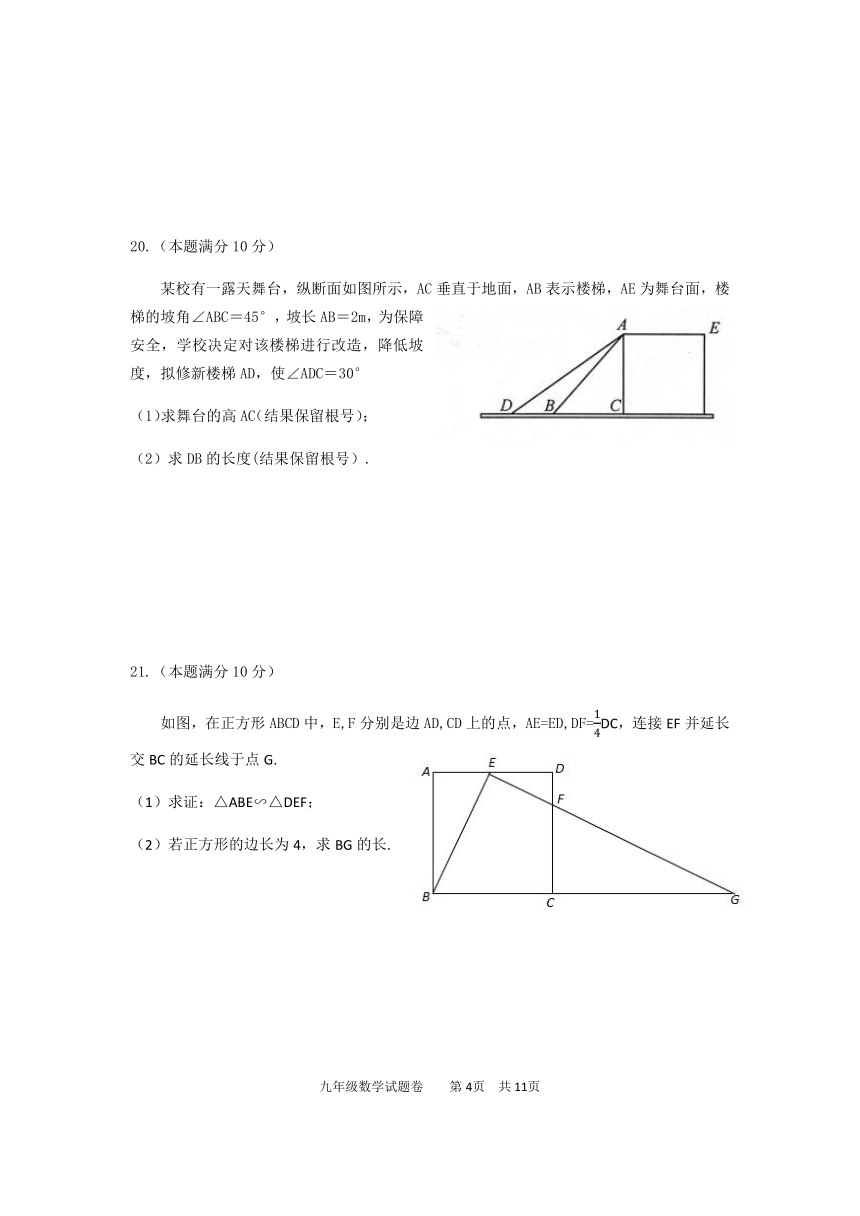
20.(本题满分10分)
某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求舞台的高AC(结果保留根号);
(2)求DB的长度(结果保留根号).
21.(本题满分10分)
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G.
求证:△ABE∽△DEF;
若正方形的边长为4,求BG的长.
22.(本题满分12分)
已知,在平面直角坐标系中,抛物线的顶点为A,点B的坐标为(3 , 5).
求抛物线过点B时顶点A的坐标;
点A的坐标记为(,),求关于的函数表达式;
已知C点的坐标为(0, 2),当m取何值时,抛物线与线段BC只有一个交点.
(本题满分12分)
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F,连接AD , GD , GC.
求证:∠ADG=∠F;
已知AE=CD, BE=2.
求⊙O的半径长;
若点G是AF的中点,求△CDG与△ADG的面积之比.
2021学年第二学期九年级期初独立作业 数学试题卷
参考答案和评分标准
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D B C A D B D D
二、填空题(本题有6小题,每小题4分,共24分)
11.1 12. 13.014.11 15.或 16. 2
三、解答题(本题有7小题,共66分)
17.(本题满分6分)
(1)画树状图如答图,
…………… …………………………(3分)
(2)共有9种等可能的结果,两次摸出的球都是红球的有1种,
∴P(两次摸出的球都是红色)= ………………………… ……………(3分)
18. (本题满分8分)
(1)b=-4 , c=3 ………………………………………(4分)
(2)顶点坐标为(2,-1),对称轴为直线x=2. ………………………………(4分)
19. (本题满分8分)
(1)∵∠A和∠D 都对 ∴∠A=∠D
又∵∠CED=∠BEA ∴ΔABE∽ΔDCE
连接BC,∵AB是直径 ∴∠ACB=90°
∵EC=2,tan∠CEB=2 ∴BC=EC×tan∠CEB=4
在中,由勾股定理得
∴BE== ……………………………………(4分)
(2)∵C为的中点 ∴= ∴DC=BC=4
∵ΔABE∽ΔDCE ∴,即
∴AB= ∴S⊙O=()2π = 20π …………………………(4分)
20. (本题满分10分)
(1)∵AB=2m,∠ABC=45°, ∴AC=BC==AB·sin45°== ……………(5分)
(2)∵∠ADC=30° ∴ CD== =
∴BD=CD-BC=(5分)…………………………………(5分)
21.(本题满分10分)
(1)在正方形ABCD中,AB=BC=CD=DA,∠A=∠D=90°
∵AE=ED ∴
∵DF=DC ∴ ∴
∴△ABE∽△DEF……………(5分)
(2)在正方形ABCD中,ED//EG ∴△DEF∽△CGF ∴
∵DF=DC ,正方形的边长为4 ∴ED=2,
∴CG=6 ∴BG=BC+CG=10……………(5分)
22.(本题满分12分)
…………………………(4分) …………………………(4分)
…………………………(4分)
23.(本题满分12分)
………………………(4分)
…………………………(4分)
…………………………(4分)九年级数学试题卷 第4页 共4页
满分120分 考试时间100分钟
一、选择题(本大题共有10个小题,每小题3分,共30分)
1.抛物线的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
2.若⊙O的半径为5cm,点A到圆心O的距离为4cm,则点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上 C.点A在圆内 D.不能确定
3.九年级(1)班在参加学校4×100m接力赛时,安排了甲、乙、丙、丁四位同学,他们的顺序由抽签随机决定,则甲同学跑第一棒的概率为( )
A.1 B. C. D.
4.若线段AB=2,点P是线段AB的黄金分割点,且APBP,则AP的长为( )
A. B. C. D.
5.如图,是⊙O的直径,点C、D是圆上两点,且∠AOC=,则∠CDB=( )
A. B. C. D.
6.若A(-6, ),B(-3, ),C(1, )为二次函数图象上的三点,则 的大小关系是( )
A. B. C. D.
7.在中,∠C=,AB=4, ,则的长为( )
A.3 B.2 C. D.
8.如图,ΔABC的中线AD,BE交于点F,EG∥BC,交AD于点G,则等于( )
A. 1:2 B. 1:3 C. 2:3 D. 3:5
9.已知二次函数(其中),下列说法正确的是( )
A.当时,都有随着的增大而增大
B.当时,都有随着的增大而减小
C.若时,都有随着的增大而减小,则
D.若时,都有随着的增大而减小,则
10. 如图,半圆O的直径AB=10,弦AC=6,D是的中点,则弦AD的长为( )
A. B.8 C. D.
二、填空题(本大题共有6个小题,每小题4分,共24分)
11.计算=__________.
12.在一个不透明的袋中装有只有颜色不同的10个球,其中6个红色,4个白色,从袋中任意摸出一个球是红球的概率是__________.
13.已知二次函数,函数y与自变量x的部分对应值如下表:
则当y<5时,x的取值范围是__________.
14.如图,在ABCD中,E是AD边上一点,AE:ED=1:2,连结AC,BE交于点F.若,则 = _________.
15.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3,AB=8,则OP长为___________.
16.如图,△ABC内接于半径为的半圆O中,AB为直径,点M是的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,∠ADB=135°且D为BM的中点,则DM的长为___________;BC的长为___________.
三、解答题(本大题共有7小题,共66分)
17.(本题满分6分)
一只不透明的袋子中装有1个红球、2个黄球,这些球除颜色外都相同。小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球。
(1)用画树状图或列表法列出摸出球的所有等可能情况;
(2)求出两次摸出的球都是红色的概率.
18. (本题满分8分)
二次函数的图象经过点(4,3)和(3,0)
(1)求b,c的值;
(2)求出该二次函数图象的顶点坐标和对称轴.
19.(本题满分8分)
如图所示,AB是⊙O的直径,弦AC、BD相交于点E,且C为的中点。若EC=2,tan∠CEB=2.
(1)求证:ΔABE∽ΔDCE,并求出BE的长;
(2)求⊙O的面积.
20.(本题满分10分)
某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求舞台的高AC(结果保留根号);
(2)求DB的长度(结果保留根号).
21.(本题满分10分)
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G.
求证:△ABE∽△DEF;
若正方形的边长为4,求BG的长.
22.(本题满分12分)
已知,在平面直角坐标系中,抛物线的顶点为A,点B的坐标为(3 , 5).
求抛物线过点B时顶点A的坐标;
点A的坐标记为(,),求关于的函数表达式;
已知C点的坐标为(0, 2),当m取何值时,抛物线与线段BC只有一个交点.
(本题满分12分)
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F,连接AD , GD , GC.
求证:∠ADG=∠F;
已知AE=CD, BE=2.
求⊙O的半径长;
若点G是AF的中点,求△CDG与△ADG的面积之比.
2021学年第二学期九年级期初独立作业 数学试题卷
参考答案和评分标准
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D B C A D B D D
二、填空题(本题有6小题,每小题4分,共24分)
11.1 12. 13.0
三、解答题(本题有7小题,共66分)
17.(本题满分6分)
(1)画树状图如答图,
…………… …………………………(3分)
(2)共有9种等可能的结果,两次摸出的球都是红球的有1种,
∴P(两次摸出的球都是红色)= ………………………… ……………(3分)
18. (本题满分8分)
(1)b=-4 , c=3 ………………………………………(4分)
(2)顶点坐标为(2,-1),对称轴为直线x=2. ………………………………(4分)
19. (本题满分8分)
(1)∵∠A和∠D 都对 ∴∠A=∠D
又∵∠CED=∠BEA ∴ΔABE∽ΔDCE
连接BC,∵AB是直径 ∴∠ACB=90°
∵EC=2,tan∠CEB=2 ∴BC=EC×tan∠CEB=4
在中,由勾股定理得
∴BE== ……………………………………(4分)
(2)∵C为的中点 ∴= ∴DC=BC=4
∵ΔABE∽ΔDCE ∴,即
∴AB= ∴S⊙O=()2π = 20π …………………………(4分)
20. (本题满分10分)
(1)∵AB=2m,∠ABC=45°, ∴AC=BC==AB·sin45°== ……………(5分)
(2)∵∠ADC=30° ∴ CD== =
∴BD=CD-BC=(5分)…………………………………(5分)
21.(本题满分10分)
(1)在正方形ABCD中,AB=BC=CD=DA,∠A=∠D=90°
∵AE=ED ∴
∵DF=DC ∴ ∴
∴△ABE∽△DEF……………(5分)
(2)在正方形ABCD中,ED//EG ∴△DEF∽△CGF ∴
∵DF=DC ,正方形的边长为4 ∴ED=2,
∴CG=6 ∴BG=BC+CG=10……………(5分)
22.(本题满分12分)
…………………………(4分) …………………………(4分)
…………………………(4分)
23.(本题满分12分)
………………………(4分)
…………………………(4分)
…………………………(4分)九年级数学试题卷 第4页 共4页
同课章节目录
