华东师大版八年级下册数学第17章函数及其图象复习课(第2课时)教案(表格式)
文档属性
| 名称 | 华东师大版八年级下册数学第17章函数及其图象复习课(第2课时)教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览



文档简介
17函数及其图象复习课(第2课时)
教学设计内容 17函数及其图象复习课(第2课时)
设计主题 《一次函数与三角形面积》
所用教科书 华东师范大学出版社八年级《数学》下册
教学对象 八年级学生
课型 复习课
执教者
一、内容分析 1.课标(2011版)要求 能用一次函数解决简单实际问题。 2.教材分析 知识层面:《函数及其图象》是华东师范大学出版社八年级《数学》下册第17章的教学内容。一次函数是初中数学中的一种最简单、最基本的函数,是反映现实世界的数量关系和变化规律的常见数学模型之一,是初中数学中的一个重点。这个复习题是学习一次函数及其应用后的巩固与概括,又为九年级学习二次函数夯实基础。 能力层面:课标要求数学教学活动必须建立在学生的认知发展水平和己有的知识经验基础之上。本节课通过《一次函数与三角形面积》的专题研究,采取由浅入深的引导,调动学生关于一次函数已有的知识和求三角形面积的相关经验,经过讨论、探究,引导学生能清晰、有条理的表达自己的思考过程;能运用数学语言,合乎逻辑的进行讨论与质疑。 思想层面:运用运动变化的观点揭示知识的发生过程以及相关知识间的内在联系,渗透数形结合、分类讨论、整体转化、方程等数学思想方法,有助于提高学生的数学思维。通过动手画图、自主探究,加强对数学思想方法的渗透,使学生不断由 “学会”向“会学”发展。 3.学情分析 八年级下的学生,已经有了一定的解决问题、自主探究问题的能力,因此,在教学上,除了基础知识的掌握,探究归纳一些问题,是必需的。在本节课学习之前,学生已较好地掌握了一次函数的定义,一次函数的图象和性质以及解决简单的函数面积的相关内容,并且完成了复习题的讲解,特别是教科书第70页第15题的学习。但对求平面直角坐标系中任意三角形面积的方法还没有灵活掌握。 4.设计意图 一次函数在中考中占有重要的地位,主要考察一次函数关系式的确定、图像和性质的分析以及实际应用等。将一次函数的图象与三角形面积综合在一起的问题,是考査学生综合素质和能力的热点题型,已成为中考命题的集点。 教材中一次函数涉及到面积问题的练习很少,无论是例题还是习题都没有归类,不利于学生系统地掌握解决问题的方法。复习题设计两课时:第一课时讲解书本复习题1——15题,本节是第2课时,本次授课是在学习本章的内容、小结、讲解复习题之后进行的专题复习题。刚好是第15题的巩固、归纳、延伸。 通过本节课的学习,让学生获得求平面直角坐标系内任意三角形的面积的通用方法。
二、教学目标: 1、知识技能:能根据题意画图,能利用直线解析式求三角形的面积,能利用面积求点坐标。 2、数学能力:通过动点的坐标与三角形面积的关系的探究,使学生体会数形结合思想,发展合情推理,进一步学习有条理地思考与表达,培养学生的探索能力和合作交流的习惯,尝试从不同角度寻求解决问题的方法,提高解决问题的能力和归纳能力。 3、数学思想:感受数学学习的乐趣,增加学习数学的兴趣和自信心。
三、教学重难点 1、重点:根据一次函数解析式求三角形的面积,探究求平面直角坐标系内任意三角形的面积的通用方法。 2、难点:根据题意画图, 探究动直线与三角形面积的关系。
四、教学策略:自主参与,合作探究
五、课前准备: 教师:课件、微课、几何画板、教学设计、学案 学生:复习第17章《函数及其图象》 ,看微课(教科书第70页第15题的讲解), 完成《学案》
六、教学过程:
教学 环节 教 学 内 容 教 师 活 动 学 生 活 动 设 计 意 图 达 成 目 标
回 忆 一次函数的解析式 是 它的图象是___ 提问 学生共同回答 由于前一节课已经对本章内容小节,因此这里只是简单回忆 复习旧知
探 究 一 母题:如图,直线a的解析式为y=2x+4,它与x轴、y轴分别相交于点A、B,点P(xp,yp)是直线a上的一个动点。 (1)求△OAB的面积。 1、多媒体展示母题, 2、提问: (1)点A、B如何求?(2)如何画图? (3)△OAB是一个什么三角形?如何求面积? 思考,回答问题 抛出问题,渗透数形结合思想、方程思想 掌握直线与坐标轴的交点坐标的求法, 及直线与两坐标轴围成的三角形的面积求法。
归 纳 总 结 一 一线两轴: 1、三角形的两条边在坐标轴上 教师补充,师生共同完成小结 学生概括,并写在学案上 对第一类型及时归纳,培养学生归纳能力 掌握一线两轴的求法
2、直线y=kx+b与y轴交于点A(0,b),与x轴
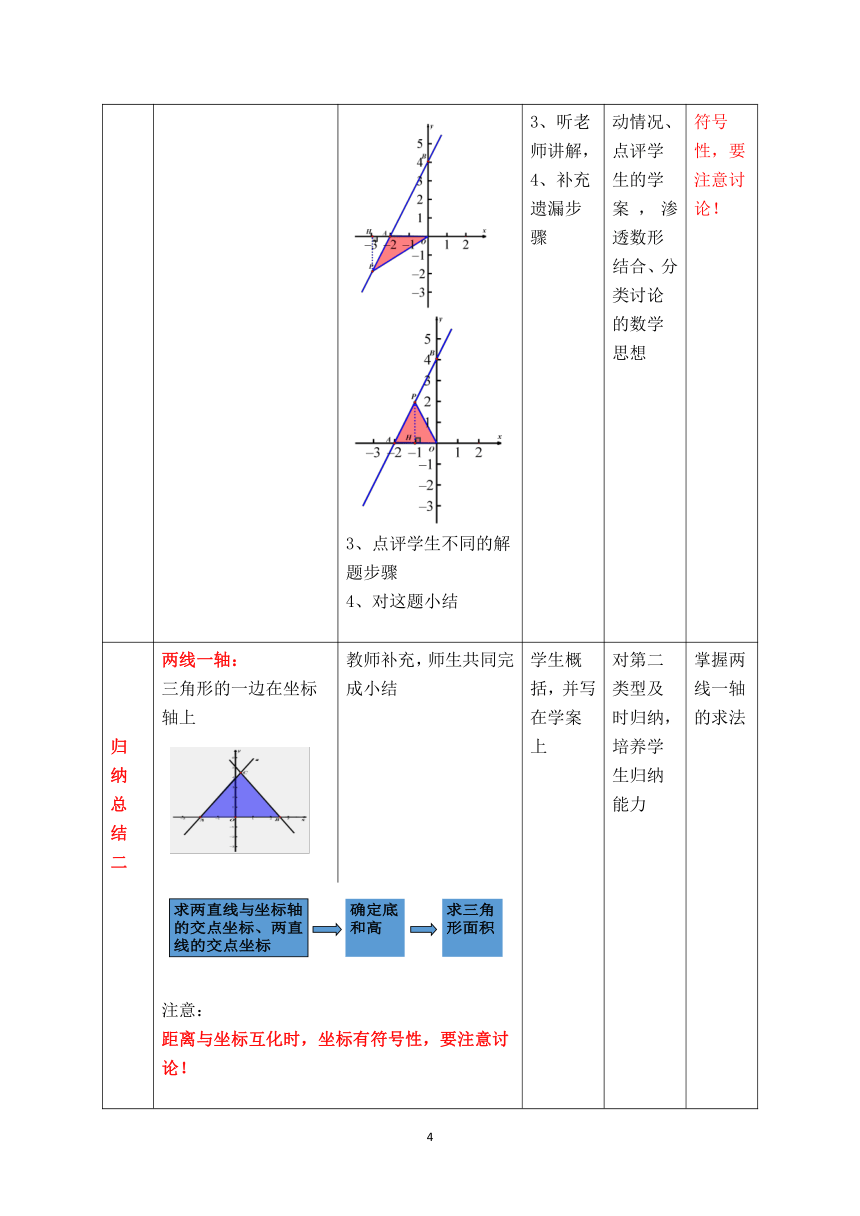
探 究 二 (2)当点P运动过程中,试写出△AOP的面积S1与x的函数关系式。 1、教师边巡视,边指导学有困难的学生,并把不同解法的答案利用希沃授课助手拍照上传 2、几何画板演示点P运动情况 3、点评学生不同的解题步骤 4、对这题小结 1、学生独立思考,完成学案, 2、同桌交流, 3、听老师讲解, 4、补充遗漏步骤 通过动手画图、自主探究、几何画板演示点P运 动情况、点评学生的学案 , 渗透数形结合、分类讨论的数学思想 让学生体会:距离与坐标互化时,坐标有 符号性,要注意讨论!
归 纳 总 结 二 两线一轴: 三角形的一边在坐标轴上 教师补充,师生共同完成小结 学生概括,并写在学案上 对第二类型及时归纳,培养学生归纳能力 掌握两线一轴的求法
注意: 距离与坐标互化时,坐标有符号性,要注意讨论!
探 究 三 (3)当点P在第三象限时,将直线a在x轴下方的部分沿x轴翻折至上方,点P对应点为点P′,试求△ABP ′的面积S2与x的函数关系式。 1、提出问题: (1)点P在直线a上,如何表示点P的坐标? (2)点P关于x轴的对称点P′的坐标如何表示? (3)直线a在x轴下方的部分沿x轴翻折至上方,如何画? 2、巡视、个别指导 3、提问学生的解题思路, 老师利用几何画板演示解法,并引导学生选择简单解法 4、师生共同完成解答 1、回答老师提出的问题 2、独立思考,根据教师的问题提示画图 3、在学案上写出解答过程 4、学生互相交流、质疑 5、踊跃发言,讲解不同的解题思路 经过讨论、探究,引导学生能清晰、有条理的表达自己的思考过程,尝试从不同角度寻求解决问题的方法,提高解决问题的能力,突出本节课的重点。 让学生获得求平面直角坐标系内任意三角形的面积的方法
归 纳 总 结 三 三 线: 三角形的三边都不在坐标轴上 教师结合图象讲解求平面直角坐标系内任意三角形的面积的通用方法,师生共同完成小结 学生概括,并写在学案上 对第三类型及时归纳,培养学生归纳能力 掌握求平面直角坐标系内任意三角形的面积的通用方法。
探 究 四 (4)平行于直线a的直线m从原点出发,沿x轴的负方向以每秒1个单位长度的速度运动,它与x轴、y轴分别相交于M、N两点,以MN为对角线作长方形OMCN,记△CMN和△OAB重合部分的面积为S3 ,设运动时间为t秒(0课 堂 小 结 师生共同完成 通过小结,提高学生归纳能力。 掌握求平面直角坐标系内直线所产生的三角形面积的方法。
注意:距离与坐标互化时,坐标有符号性,距离有非负性!
作 业 见学案 课后完成 学生利用所学知识,自测掌握情况。分必做题和选做题,是针对不同层次的学生而设计的。 掌握本节课所学知识,学以致用。
结 束 语 幸福之神的降临 往往是因为你 多看了一眼 多想了一下 多走了一步 多给学生鼓励,让学生感受学习数学的乐趣,增加学习数学的兴趣和自信心。
七、教学反思: 1、授课流程反思: 以“母题”为主线,设计探究(一)~(四),环环相扣,层层深入,突出了本节课的教学重点,符合学生的认知规律,较好地实现了本节课的课程目标。 2、授课效果反思: (1)通过创设问题情景,以问题驱动引领学生思维。较好地落实了“四基”,即数学的基础知识、基本技能、基本思想和基本活动经验。以课件为载体,变教为探,让学生经历知识的形成过程,提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力,即:四能。从而突破了本节课的难点。 (2)从课堂交流看,学生已养成独立思考问题的能力,踊跃发言,能清晰、有条理的表达自己的思考过程,能从不同角度寻求解决问题的方法,并能对同学的思路提出质疑。 (3)不足之处:①考虑到是复习课,且学生已经有一定的求面积的知识储备,设计探究的容量有点多,因此只能在上课前一天分给学生去思考。②由于是公开课,学生比较拘谨。③第三类题型三线还有以下两种解法, 授课时没有考虑到,因此制作微课“平面直角坐标系中任意三角形的面积求法小结”,发给学生,让学生通过反复观察,加深理解,掌握方法。
(
9
)
教学设计内容 17函数及其图象复习课(第2课时)
设计主题 《一次函数与三角形面积》
所用教科书 华东师范大学出版社八年级《数学》下册
教学对象 八年级学生
课型 复习课
执教者
一、内容分析 1.课标(2011版)要求 能用一次函数解决简单实际问题。 2.教材分析 知识层面:《函数及其图象》是华东师范大学出版社八年级《数学》下册第17章的教学内容。一次函数是初中数学中的一种最简单、最基本的函数,是反映现实世界的数量关系和变化规律的常见数学模型之一,是初中数学中的一个重点。这个复习题是学习一次函数及其应用后的巩固与概括,又为九年级学习二次函数夯实基础。 能力层面:课标要求数学教学活动必须建立在学生的认知发展水平和己有的知识经验基础之上。本节课通过《一次函数与三角形面积》的专题研究,采取由浅入深的引导,调动学生关于一次函数已有的知识和求三角形面积的相关经验,经过讨论、探究,引导学生能清晰、有条理的表达自己的思考过程;能运用数学语言,合乎逻辑的进行讨论与质疑。 思想层面:运用运动变化的观点揭示知识的发生过程以及相关知识间的内在联系,渗透数形结合、分类讨论、整体转化、方程等数学思想方法,有助于提高学生的数学思维。通过动手画图、自主探究,加强对数学思想方法的渗透,使学生不断由 “学会”向“会学”发展。 3.学情分析 八年级下的学生,已经有了一定的解决问题、自主探究问题的能力,因此,在教学上,除了基础知识的掌握,探究归纳一些问题,是必需的。在本节课学习之前,学生已较好地掌握了一次函数的定义,一次函数的图象和性质以及解决简单的函数面积的相关内容,并且完成了复习题的讲解,特别是教科书第70页第15题的学习。但对求平面直角坐标系中任意三角形面积的方法还没有灵活掌握。 4.设计意图 一次函数在中考中占有重要的地位,主要考察一次函数关系式的确定、图像和性质的分析以及实际应用等。将一次函数的图象与三角形面积综合在一起的问题,是考査学生综合素质和能力的热点题型,已成为中考命题的集点。 教材中一次函数涉及到面积问题的练习很少,无论是例题还是习题都没有归类,不利于学生系统地掌握解决问题的方法。复习题设计两课时:第一课时讲解书本复习题1——15题,本节是第2课时,本次授课是在学习本章的内容、小结、讲解复习题之后进行的专题复习题。刚好是第15题的巩固、归纳、延伸。 通过本节课的学习,让学生获得求平面直角坐标系内任意三角形的面积的通用方法。
二、教学目标: 1、知识技能:能根据题意画图,能利用直线解析式求三角形的面积,能利用面积求点坐标。 2、数学能力:通过动点的坐标与三角形面积的关系的探究,使学生体会数形结合思想,发展合情推理,进一步学习有条理地思考与表达,培养学生的探索能力和合作交流的习惯,尝试从不同角度寻求解决问题的方法,提高解决问题的能力和归纳能力。 3、数学思想:感受数学学习的乐趣,增加学习数学的兴趣和自信心。
三、教学重难点 1、重点:根据一次函数解析式求三角形的面积,探究求平面直角坐标系内任意三角形的面积的通用方法。 2、难点:根据题意画图, 探究动直线与三角形面积的关系。
四、教学策略:自主参与,合作探究
五、课前准备: 教师:课件、微课、几何画板、教学设计、学案 学生:复习第17章《函数及其图象》 ,看微课(教科书第70页第15题的讲解), 完成《学案》
六、教学过程:
教学 环节 教 学 内 容 教 师 活 动 学 生 活 动 设 计 意 图 达 成 目 标
回 忆 一次函数的解析式 是 它的图象是___ 提问 学生共同回答 由于前一节课已经对本章内容小节,因此这里只是简单回忆 复习旧知
探 究 一 母题:如图,直线a的解析式为y=2x+4,它与x轴、y轴分别相交于点A、B,点P(xp,yp)是直线a上的一个动点。 (1)求△OAB的面积。 1、多媒体展示母题, 2、提问: (1)点A、B如何求?(2)如何画图? (3)△OAB是一个什么三角形?如何求面积? 思考,回答问题 抛出问题,渗透数形结合思想、方程思想 掌握直线与坐标轴的交点坐标的求法, 及直线与两坐标轴围成的三角形的面积求法。
归 纳 总 结 一 一线两轴: 1、三角形的两条边在坐标轴上 教师补充,师生共同完成小结 学生概括,并写在学案上 对第一类型及时归纳,培养学生归纳能力 掌握一线两轴的求法
2、直线y=kx+b与y轴交于点A(0,b),与x轴
探 究 二 (2)当点P运动过程中,试写出△AOP的面积S1与x的函数关系式。 1、教师边巡视,边指导学有困难的学生,并把不同解法的答案利用希沃授课助手拍照上传 2、几何画板演示点P运动情况 3、点评学生不同的解题步骤 4、对这题小结 1、学生独立思考,完成学案, 2、同桌交流, 3、听老师讲解, 4、补充遗漏步骤 通过动手画图、自主探究、几何画板演示点P运 动情况、点评学生的学案 , 渗透数形结合、分类讨论的数学思想 让学生体会:距离与坐标互化时,坐标有 符号性,要注意讨论!
归 纳 总 结 二 两线一轴: 三角形的一边在坐标轴上 教师补充,师生共同完成小结 学生概括,并写在学案上 对第二类型及时归纳,培养学生归纳能力 掌握两线一轴的求法
注意: 距离与坐标互化时,坐标有符号性,要注意讨论!
探 究 三 (3)当点P在第三象限时,将直线a在x轴下方的部分沿x轴翻折至上方,点P对应点为点P′,试求△ABP ′的面积S2与x的函数关系式。 1、提出问题: (1)点P在直线a上,如何表示点P的坐标? (2)点P关于x轴的对称点P′的坐标如何表示? (3)直线a在x轴下方的部分沿x轴翻折至上方,如何画? 2、巡视、个别指导 3、提问学生的解题思路, 老师利用几何画板演示解法,并引导学生选择简单解法 4、师生共同完成解答 1、回答老师提出的问题 2、独立思考,根据教师的问题提示画图 3、在学案上写出解答过程 4、学生互相交流、质疑 5、踊跃发言,讲解不同的解题思路 经过讨论、探究,引导学生能清晰、有条理的表达自己的思考过程,尝试从不同角度寻求解决问题的方法,提高解决问题的能力,突出本节课的重点。 让学生获得求平面直角坐标系内任意三角形的面积的方法
归 纳 总 结 三 三 线: 三角形的三边都不在坐标轴上 教师结合图象讲解求平面直角坐标系内任意三角形的面积的通用方法,师生共同完成小结 学生概括,并写在学案上 对第三类型及时归纳,培养学生归纳能力 掌握求平面直角坐标系内任意三角形的面积的通用方法。
探 究 四 (4)平行于直线a的直线m从原点出发,沿x轴的负方向以每秒1个单位长度的速度运动,它与x轴、y轴分别相交于M、N两点,以MN为对角线作长方形OMCN,记△CMN和△OAB重合部分的面积为S3 ,设运动时间为t秒(0
注意:距离与坐标互化时,坐标有符号性,距离有非负性!
作 业 见学案 课后完成 学生利用所学知识,自测掌握情况。分必做题和选做题,是针对不同层次的学生而设计的。 掌握本节课所学知识,学以致用。
结 束 语 幸福之神的降临 往往是因为你 多看了一眼 多想了一下 多走了一步 多给学生鼓励,让学生感受学习数学的乐趣,增加学习数学的兴趣和自信心。
七、教学反思: 1、授课流程反思: 以“母题”为主线,设计探究(一)~(四),环环相扣,层层深入,突出了本节课的教学重点,符合学生的认知规律,较好地实现了本节课的课程目标。 2、授课效果反思: (1)通过创设问题情景,以问题驱动引领学生思维。较好地落实了“四基”,即数学的基础知识、基本技能、基本思想和基本活动经验。以课件为载体,变教为探,让学生经历知识的形成过程,提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力,即:四能。从而突破了本节课的难点。 (2)从课堂交流看,学生已养成独立思考问题的能力,踊跃发言,能清晰、有条理的表达自己的思考过程,能从不同角度寻求解决问题的方法,并能对同学的思路提出质疑。 (3)不足之处:①考虑到是复习课,且学生已经有一定的求面积的知识储备,设计探究的容量有点多,因此只能在上课前一天分给学生去思考。②由于是公开课,学生比较拘谨。③第三类题型三线还有以下两种解法, 授课时没有考虑到,因此制作微课“平面直角坐标系中任意三角形的面积求法小结”,发给学生,让学生通过反复观察,加深理解,掌握方法。
(
9
)
