华东师大版七年级下册数学 8.2.3 解一元一次不等式(1) 课件(共14张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.2.3 解一元一次不等式(1) 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1020.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 19:50:31 | ||
图片预览






文档简介
(共14张PPT)
解一元一次不等式
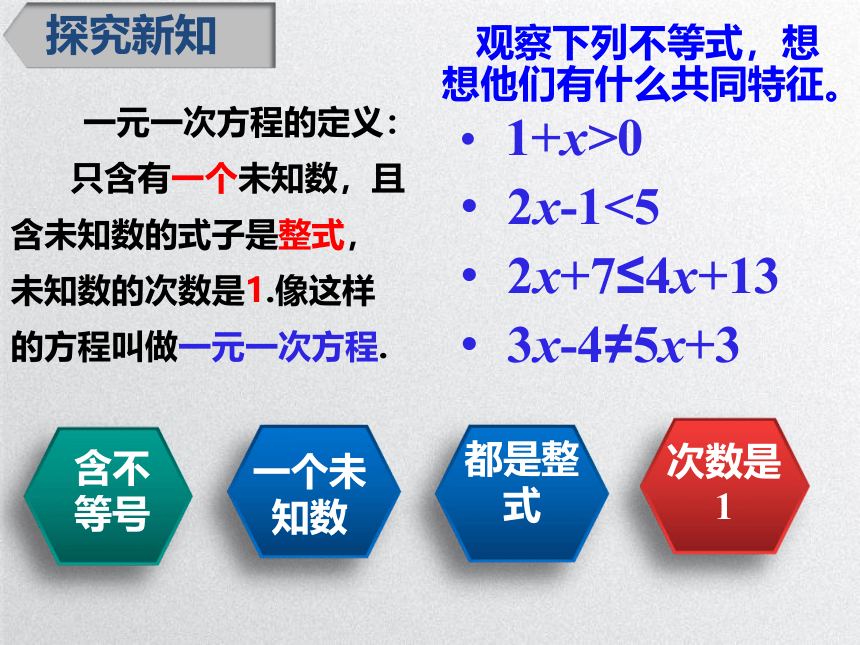
观察下列不等式,想想他们有什么共同特征。
1+x>0
2x-1<5
2x+7≤4x+13
3x-4≠5x+3
含不等号
都是整式
次数是1
探究新知
一个未知数
一元一次方程的定义:
只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.像这样的方程叫做一元一次方程.
只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.像这样的不等式叫做一元一次不等式.
一元一次不等式的定义
探究新知
判断下列各式是不是一元一次不等式?
①2a-1=4a+9; ( )
②3y-6 >3x+7; ( )
③ <5; ( )
④x2>1; ( )
⑤2x+6≤x. ( )
判断一元一次不等式条件
(1)含有不等号
(2)只含有一个未知数
(3)整式
(4)未知数次数是“1”
小试牛刀
是
不是
不是
不是
不是
(2) :解下列不等式,并将解集在数轴上表示出来: 2x-1<4x+13
解: 2x-1<4x+13
1
2
-2
-1
0
-4
-5
-6
-7
-8
-3
探究新知
例1: (1)解方程
2x-1=4x+13
解: 2x-1=4x+13
2x-4x=13+1
-2x=14
x=-7
它在数轴上的表示如图所示
解一元一次方程和解一元一次不等式的异同点。
步骤相同
不同点
相同点
探究新知
结果
系数化“1”
例2:解下列不等式,并将解集在数轴上表示出来:
2(5x+3)≤x-3(1-2x)
探究新知
乘除正数不变方向
切记
乘除负数要变方向
切记
探究新知
探究新知
乘除正数不变方向
切记
乘除负数要变方向
切记
小试牛刀
去分母
去括号
移项
合并同类项
系数化为1
1
2
3
4
5
归纳小结
解一元一次不等式的步骤:
乘除负数要变不等号方向
课堂练习
我们共同努力
谢谢
解一元一次不等式
观察下列不等式,想想他们有什么共同特征。
1+x>0
2x-1<5
2x+7≤4x+13
3x-4≠5x+3
含不等号
都是整式
次数是1
探究新知
一个未知数
一元一次方程的定义:
只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.像这样的方程叫做一元一次方程.
只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.像这样的不等式叫做一元一次不等式.
一元一次不等式的定义
探究新知
判断下列各式是不是一元一次不等式?
①2a-1=4a+9; ( )
②3y-6 >3x+7; ( )
③ <5; ( )
④x2>1; ( )
⑤2x+6≤x. ( )
判断一元一次不等式条件
(1)含有不等号
(2)只含有一个未知数
(3)整式
(4)未知数次数是“1”
小试牛刀
是
不是
不是
不是
不是
(2) :解下列不等式,并将解集在数轴上表示出来: 2x-1<4x+13
解: 2x-1<4x+13
1
2
-2
-1
0
-4
-5
-6
-7
-8
-3
探究新知
例1: (1)解方程
2x-1=4x+13
解: 2x-1=4x+13
2x-4x=13+1
-2x=14
x=-7
它在数轴上的表示如图所示
解一元一次方程和解一元一次不等式的异同点。
步骤相同
不同点
相同点
探究新知
结果
系数化“1”
例2:解下列不等式,并将解集在数轴上表示出来:
2(5x+3)≤x-3(1-2x)
探究新知
乘除正数不变方向
切记
乘除负数要变方向
切记
探究新知
探究新知
乘除正数不变方向
切记
乘除负数要变方向
切记
小试牛刀
去分母
去括号
移项
合并同类项
系数化为1
1
2
3
4
5
归纳小结
解一元一次不等式的步骤:
乘除负数要变不等号方向
课堂练习
我们共同努力
谢谢
