数学人教A版(2019)选择性必修第三册8.1.1变量的相关关系(共40张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.1.1变量的相关关系(共40张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 23:02:11 | ||
图片预览





文档简介
(共40张PPT)
8.1变量的相关关系
油腻大叔是怎样炼成的
年龄越大越“油”?
变量1:年龄
变量2:脂肪含量
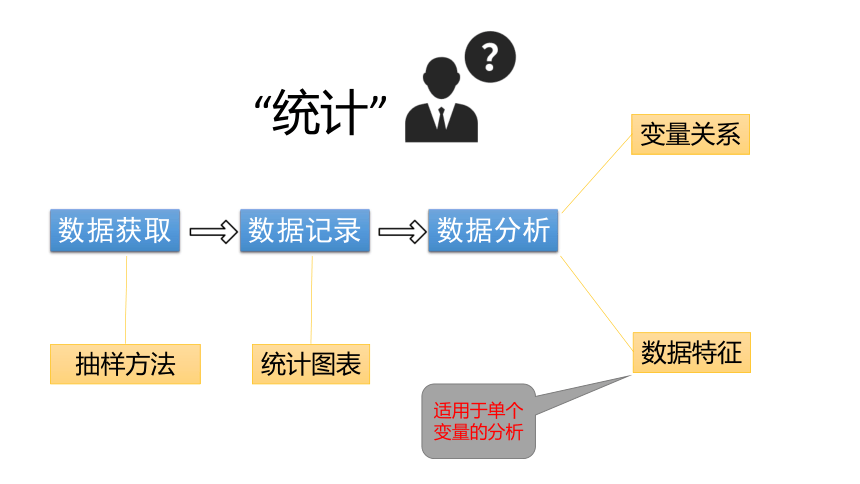
“统计”
数据获取
数据记录
数据分析
抽样方法
统计图表
数据特征
变量关系
适用于单个变量的分析
变量A:
变量B:
该从哪些角度分析两个个变量的关系?
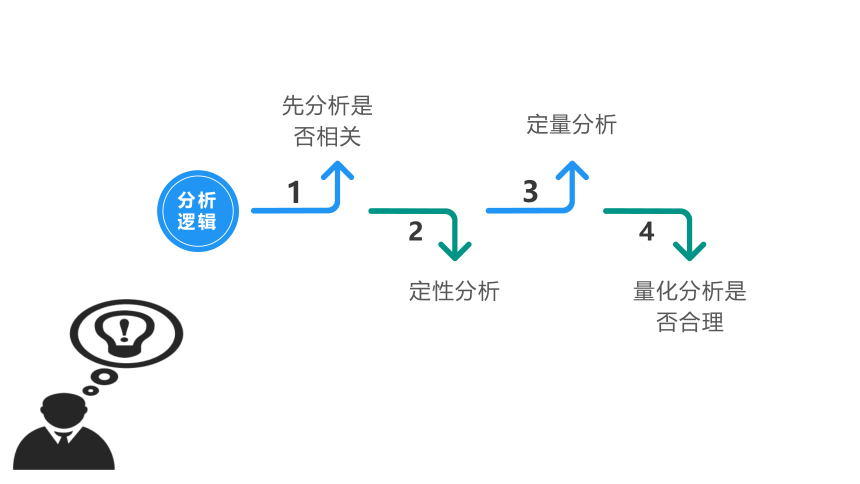
分析逻辑
1
先分析是否相关
2
定性分析
4
量化分析是否合理
3
定量分析
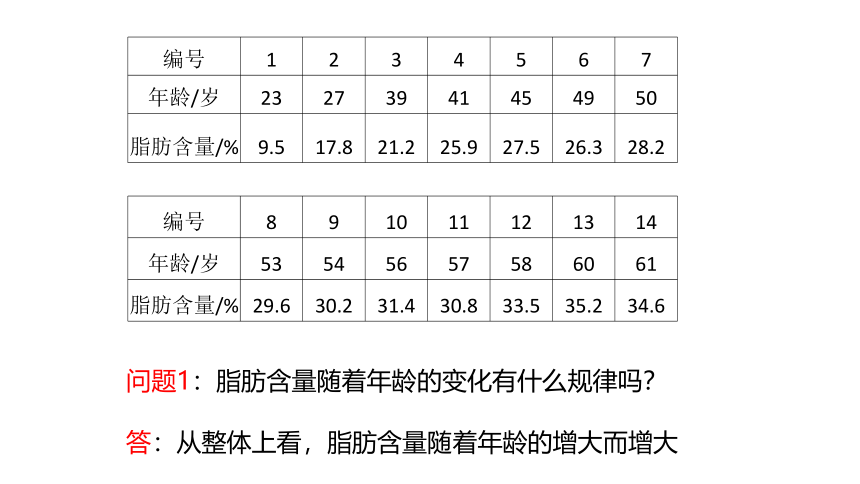
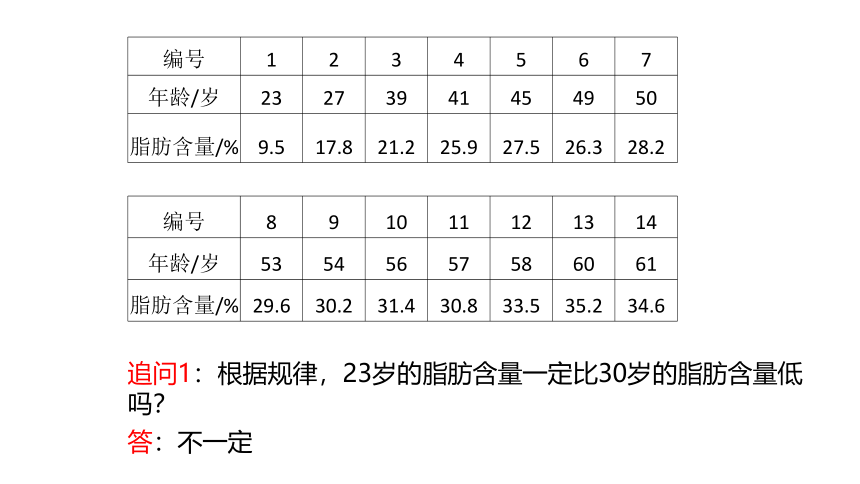
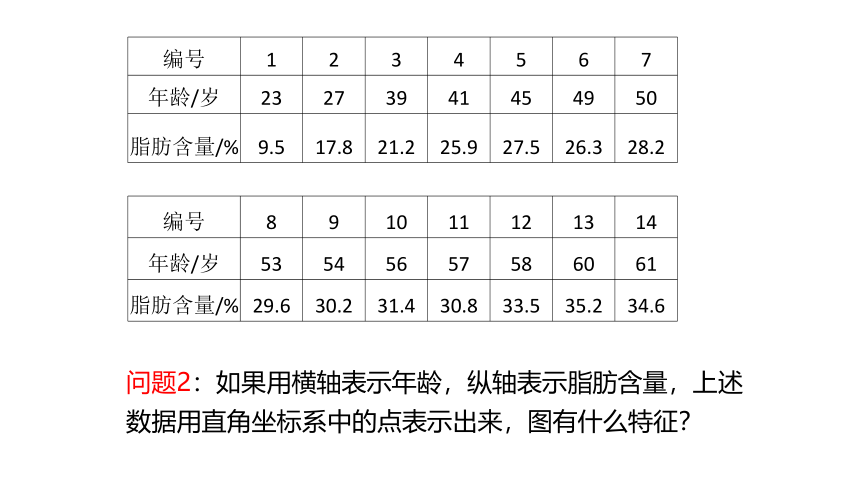
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
问题1:脂肪含量随着年龄的变化有什么规律吗?
答:从整体上看,脂肪含量随着年龄的增大而增大
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
追问1:根据规律,23岁的脂肪含量一定比30岁的脂肪含量低吗?
答:不一定
相关关系:两个变量有关系,但又没有确切到可由其中的一个精确地决定另一个,这种关系称为相关关系。
例1、判断下面两变量是否相关关系
(1)子女的身高 与父亲身高
(2)商品销售收入 与广告支出
(3)空气污染指数 与汽车保有量
(4)粮食亩产量 与施肥量
(5)正方形的面积 与正方形的边长
√
√
√
√
×
正方形面积与边长是确定关系,是函数关系,y可以由x唯一确定
相关关系与函数关系的异同点
概念辨析
是一种确定关系
是一种因果关系
函数关系
相关关系
都是两个变量间的关系
是一种非确定关系
不一定是因果关系,也可能是伴随关系
相同点
不同点
某地区的环境条件适合天鹅栖息繁衍.有人发现了一个有趣的现象,该地区有5个村庄,其中3个村庄附近栖息的天鹅较多,婴儿出生率也较高;2个村庄附近栖息的天鹅较少,婴儿的出生率也较低.有人认为婴儿出生率和天鹅数之间存在相关关系,并得出一个结论:天鹅能够带来孩子.你同意这个结论吗?
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
问题2:如果用横轴表示年龄,纵轴表示脂肪含量,上述数据用直角坐标系中的点表示出来,图有什么特征?
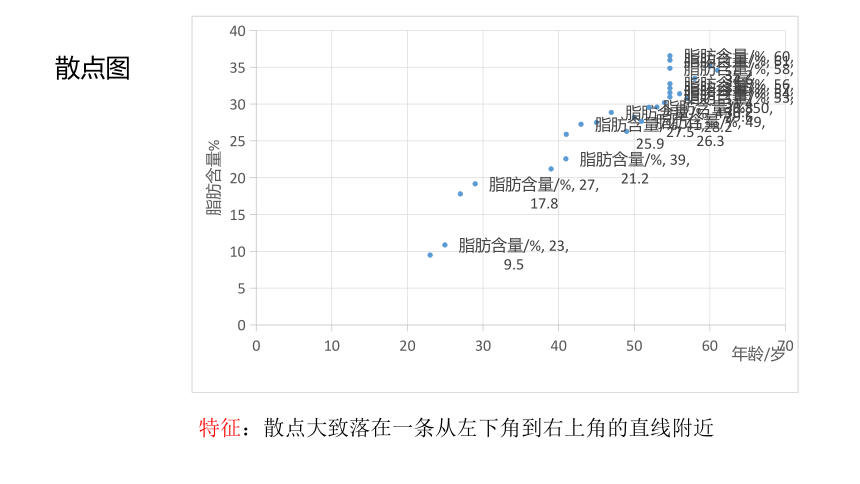
散点图
特征:散点大致落在一条从左下角到右上角的直线附近
正相关:从整体上看,当一个变量的值增加时,另一个变量的相应值
也呈现增加的趋势
负相关:从整体上看,当一个变量的值增加时,另一个变量的相应值
也呈现减少的趋势
线性相关:两个变量呈正相关或负相关,且散点图落在一条直线附近
结论:脂肪含量与年龄成线性正相关关系
练习.下列四个散点图中,变量x与y之间具有负的线性相关关系的是( )
D
问题3:这两组成对变量都是线性正相关,你能判断哪一组的线性相关性更强吗?
答:不能
探究:散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小.能否像引入平均值、方差等数字特征对单个变量数据进行分析那样,引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢
线性负相关
线性正相关
无相关关系
非线性相关
观察下面四个散点图所表示的四组成对变量 ,从两类变量 数据的正负、大小角度比较,是否有明显区别?
数据预处理的常用方法:中心化(零均值化)
对于变量 和变量 ,设经过随机抽样得到的成对数据为( 1, 1),( 2, 2), ,( , ),
将数据以为零点进行平移,得到平移后的成对数据为:
数据平移以后,作出散点图如下
线性负相关
线性正相关
无相关关系
非线性相关
(x,y)基本异号
(x,y)基本同号
一般情形下,Lxy>0表明成对样本数据正相关; Lxy <0表明成对样本数据负相关.
根据散点图特征,初步构造统计量.利用散点
的横纵坐标是否同号,可以构造一个量
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高单位由米改为厘米,单位的改变不会改变体重与身高之间的相关程度.
变换单位前
变换单位后
变换单位后是变换前的100倍
我们发现, Lxy的大小与数据的度量单位有关,所以不能直接用它度量成对样本数据相关程度的大小.
为了消除单位的影响,进一步做“标准化”处理
分别
为简单起见,把上述“标准化”处理后的成对数据分别记为
仿照Lxy的构造,可以得到
我们称r为变量x和变量y的样本线性相关系数,
简称样本相关系数.
接下来我们来考察r的合理性
当r>0时,称成对样本数据正相关;当其中一个数据的值变小时,另一个数据的值通常也变小;当其中一个数据的值变大时,另一个数据的值通常也变大。
当r<0时,称成对样本数据负相关;当其中一个数据的值变小时,另一个数据的值通常会变大:当其中一个数据的值变大时,另一个数据的值通常会变小。
问题4:样本相关系数r的正负能反映出成对变量的什么关系?
问题5:样本相关系数r的取值与成对样本数据的相关程度
有什么内在联系?
观察r的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,我们将向量的维数推广到n维,n维向量的 数量积仍然定义为
其中 为向量 的夹角.
首先我们来考察r的取值范围
类似于平面或空间向量的坐标表示,对于向量
我们有
设“标准化”处理后的成对数据
的第一分量构成n维向量
第二分量构成向量
思考: 时,成对样本数据之间有怎样的关系 ?
或
共线
由向量的共线定理得
即
这表明成对样本数据 都落在直线 上
说明成对样本数据的两个分量之间满足一种线性关系
由此可见,样本相关系数r的取值范围为[-1,1].样本相关系数r的绝对值大小可以反映成对数据之间线性相关的程度。
问题5:样本相关系数r的取值与成对样本数据的相关程度
有什么内在联系?
当|r|越接近0时,成对数据的线性相关程度越弱.
当|r|越接近1时,成对数据的线性相关程度越强;
答:
追问5:样本相关系数r=0时,样本一定是无相关关系吗?
r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
答:
小贴士:利用相关系数r来检验线性相关显著性水平时,通常与0.75作比较,若|r|>0.75,则线性相关较为显著,否则不显著.
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
例.根据下表中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本相关系数,并推断它们的相关程度.
参考数据:
由样本相关系数r≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同。
解:先画出散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关。
课堂小结
1.成对样本数据的关系类型
2.散点图判断相关关系
3.样本相关系数的计算及其意义
分析逻辑
1
先分析是否相关
2
定性分析
4
量化分析是否合理
3
定量分析
散点图
相关系数r判断线性相关程度
谢谢!
8.1变量的相关关系
油腻大叔是怎样炼成的
年龄越大越“油”?
变量1:年龄
变量2:脂肪含量
“统计”
数据获取
数据记录
数据分析
抽样方法
统计图表
数据特征
变量关系
适用于单个变量的分析
变量A:
变量B:
该从哪些角度分析两个个变量的关系?
分析逻辑
1
先分析是否相关
2
定性分析
4
量化分析是否合理
3
定量分析
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
问题1:脂肪含量随着年龄的变化有什么规律吗?
答:从整体上看,脂肪含量随着年龄的增大而增大
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
追问1:根据规律,23岁的脂肪含量一定比30岁的脂肪含量低吗?
答:不一定
相关关系:两个变量有关系,但又没有确切到可由其中的一个精确地决定另一个,这种关系称为相关关系。
例1、判断下面两变量是否相关关系
(1)子女的身高 与父亲身高
(2)商品销售收入 与广告支出
(3)空气污染指数 与汽车保有量
(4)粮食亩产量 与施肥量
(5)正方形的面积 与正方形的边长
√
√
√
√
×
正方形面积与边长是确定关系,是函数关系,y可以由x唯一确定
相关关系与函数关系的异同点
概念辨析
是一种确定关系
是一种因果关系
函数关系
相关关系
都是两个变量间的关系
是一种非确定关系
不一定是因果关系,也可能是伴随关系
相同点
不同点
某地区的环境条件适合天鹅栖息繁衍.有人发现了一个有趣的现象,该地区有5个村庄,其中3个村庄附近栖息的天鹅较多,婴儿出生率也较高;2个村庄附近栖息的天鹅较少,婴儿的出生率也较低.有人认为婴儿出生率和天鹅数之间存在相关关系,并得出一个结论:天鹅能够带来孩子.你同意这个结论吗?
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
问题2:如果用横轴表示年龄,纵轴表示脂肪含量,上述数据用直角坐标系中的点表示出来,图有什么特征?
散点图
特征:散点大致落在一条从左下角到右上角的直线附近
正相关:从整体上看,当一个变量的值增加时,另一个变量的相应值
也呈现增加的趋势
负相关:从整体上看,当一个变量的值增加时,另一个变量的相应值
也呈现减少的趋势
线性相关:两个变量呈正相关或负相关,且散点图落在一条直线附近
结论:脂肪含量与年龄成线性正相关关系
练习.下列四个散点图中,变量x与y之间具有负的线性相关关系的是( )
D
问题3:这两组成对变量都是线性正相关,你能判断哪一组的线性相关性更强吗?
答:不能
探究:散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小.能否像引入平均值、方差等数字特征对单个变量数据进行分析那样,引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢
线性负相关
线性正相关
无相关关系
非线性相关
观察下面四个散点图所表示的四组成对变量 ,从两类变量 数据的正负、大小角度比较,是否有明显区别?
数据预处理的常用方法:中心化(零均值化)
对于变量 和变量 ,设经过随机抽样得到的成对数据为( 1, 1),( 2, 2), ,( , ),
将数据以为零点进行平移,得到平移后的成对数据为:
数据平移以后,作出散点图如下
线性负相关
线性正相关
无相关关系
非线性相关
(x,y)基本异号
(x,y)基本同号
一般情形下,Lxy>0表明成对样本数据正相关; Lxy <0表明成对样本数据负相关.
根据散点图特征,初步构造统计量.利用散点
的横纵坐标是否同号,可以构造一个量
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高单位由米改为厘米,单位的改变不会改变体重与身高之间的相关程度.
变换单位前
变换单位后
变换单位后是变换前的100倍
我们发现, Lxy的大小与数据的度量单位有关,所以不能直接用它度量成对样本数据相关程度的大小.
为了消除单位的影响,进一步做“标准化”处理
分别
为简单起见,把上述“标准化”处理后的成对数据分别记为
仿照Lxy的构造,可以得到
我们称r为变量x和变量y的样本线性相关系数,
简称样本相关系数.
接下来我们来考察r的合理性
当r>0时,称成对样本数据正相关;当其中一个数据的值变小时,另一个数据的值通常也变小;当其中一个数据的值变大时,另一个数据的值通常也变大。
当r<0时,称成对样本数据负相关;当其中一个数据的值变小时,另一个数据的值通常会变大:当其中一个数据的值变大时,另一个数据的值通常会变小。
问题4:样本相关系数r的正负能反映出成对变量的什么关系?
问题5:样本相关系数r的取值与成对样本数据的相关程度
有什么内在联系?
观察r的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,我们将向量的维数推广到n维,n维向量的 数量积仍然定义为
其中 为向量 的夹角.
首先我们来考察r的取值范围
类似于平面或空间向量的坐标表示,对于向量
我们有
设“标准化”处理后的成对数据
的第一分量构成n维向量
第二分量构成向量
思考: 时,成对样本数据之间有怎样的关系 ?
或
共线
由向量的共线定理得
即
这表明成对样本数据 都落在直线 上
说明成对样本数据的两个分量之间满足一种线性关系
由此可见,样本相关系数r的取值范围为[-1,1].样本相关系数r的绝对值大小可以反映成对数据之间线性相关的程度。
问题5:样本相关系数r的取值与成对样本数据的相关程度
有什么内在联系?
当|r|越接近0时,成对数据的线性相关程度越弱.
当|r|越接近1时,成对数据的线性相关程度越强;
答:
追问5:样本相关系数r=0时,样本一定是无相关关系吗?
r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
答:
小贴士:利用相关系数r来检验线性相关显著性水平时,通常与0.75作比较,若|r|>0.75,则线性相关较为显著,否则不显著.
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
例.根据下表中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本相关系数,并推断它们的相关程度.
参考数据:
由样本相关系数r≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同。
解:先画出散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关。
课堂小结
1.成对样本数据的关系类型
2.散点图判断相关关系
3.样本相关系数的计算及其意义
分析逻辑
1
先分析是否相关
2
定性分析
4
量化分析是否合理
3
定量分析
散点图
相关系数r判断线性相关程度
谢谢!
