数学人教A版(2019)选择性必修第三册7.2离散型随机变量及其分布列(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.2离散型随机变量及其分布列(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 23:04:17 | ||
图片预览








文档简介
(共25张PPT)
7.2 离散型随机变量及其分布
2
学习目标
1.理解随机变量的意义,了解随机变量与函数的区别;
2.掌握离散型随机变量的概念,能够写出随机变量的取值以及随机试验的结果;
3.理解取有限值的离散型随机变量的分布列及两点分布的概念及表示.
4.掌握离散型随机变量的分布列的性质.
5.会求某些简单的离散型随机变量的分布列(含两点分布).
1. 随机试验
一般地,一个试验如果满足下列条件:
①试验可以在相同的情形下重复进行;
②试验的所有可能结果是明确可知的,并且不只一个;
③每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前却不能肯定这次试验
会出现哪一个结果; 这种试验就是一个随机试验,为了方便起见,也简称试验.
2. 函数
一般地,设A,B是非空的数集,如果使对于集合A中的任意一个数x ,按照某种确定的对应关系f ,在集合B中都有唯一确定的数 y 和它对应,那么就称f :A→B为从集合A到集合B的一个函数,记作:
随机试验的样本空间与实数集之间能否建立某种对应关系呢?
知识回顾
数学活动1
探究1.有些随机试验的样本空间与数值有关系,我们可以直接与实数建立关系.
(1)掷一枚骰子用实数 ( =1,2,3,4,5,6)表示“掷出的点数为 ”,又如,掷两枚骰子样本空间为Ω={ ( , ) | , =1,2, 6},用 + 表示“两枚骰子的点数之和”样本点( , )就与实数 + 对应.
(2)某射击运动员在射击训练中,其中某次射击可能出现命中的环数情况有哪些?
实数 ( =0,1,2,3,4,5,6,···,10)表示“击中环数 ”
(0环、1环、2环、···、10环)共11种结果
探究2. 考察下列随机试验及其引入的变量:
试验1: 从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验,变量X 表示三个元件中次品数;
试验2: 抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么 各个样本点与变量的值是如何对应的
数学活动1
数学活动1
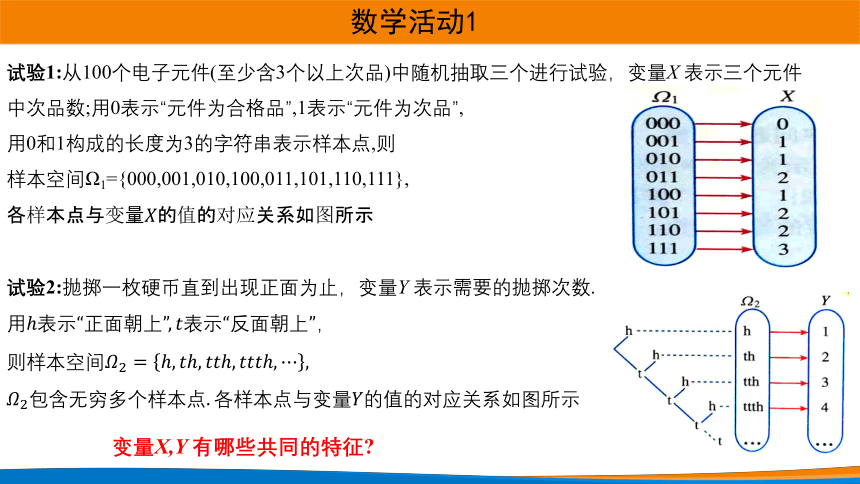
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验,变量X 表示三个元件中次品数;用0表示“元件为合格品”,1表示“元件为次品”,
用0和1构成的长度为3的字符串表示样本点,则
样本空间Ω1={000,001,010,100,011,101,110,111},
试验2:抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
变量X,Y 有哪些共同的特征
学习新知
1.随机变量的定义
2.离散型随机变量的定义
随机变量的特点
可以用数字表示
试验之前可以判断其可能出现的所有值
在试验之前不可能确定取何值
随机变量将随机事件的结果数量化.
例1.写出下列各随机变量可能的取值,并说明随机变量所取值所表示的随机试验的结果:
(1)从10张已编号的卡片(从1号到10号)中任取1张,被取出的卡片的号数X 。
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球数X.
(3)抛掷两个骰子,所得点数之和X.
(4)某射击运动员射击一次可能命中的环数X .
(5)某一自动装置无故障运转的时间X.
(6)某林场树木最高达30米,此林场树木的高度X .
解:(1)X =1、2、3、···、10;(2)X=0、1、2、3;
(3)X=2、3、4、···、12;(4) X=0、1、2、3、···、10;
(5) X取内的一切值;(6)X取内的一切值.
学习新知
学习新知
学习新知
思考1.下列变量中是离散型随机变量的是?
(1)下期《诗词大会》节目中过关的人数;
(2)某加工厂加工的一批某种钢管的外径与规定的外径尺寸之差;
(3)在郑州至武汉的电气化铁道线上,每隔50 m有一电线铁塔,从郑州至武汉的电气化铁道线上将电线铁塔进行编号,其中某一电线铁塔的编号;
(4)江西九江市长江水位监测站所测水位在(0,29]这一范围内变化,该水位站所测水位.
答案:(1)(3)
变式探究: 将本题的(4)改为:监测站所测水位X是否超过警戒水位(警戒水位是29 m),X是离散型随机变量吗
12
学习新知
解析式法:P(X=xi)= pi , i=1,2,3…,n
图象法:
2. 函数可以用解析式、表格、图象表示。离散型随机变量的分布列也可以用解析式、表格、图象表示。
X x1 x2 … xk … xn
P p1 p2 … pk … pn
表格法:
学习新知
3.离散型随机变量的分布列具有下述两个性质:
注意:① 列出随机变量的所有可能取值;
② 求出随机变量的每一个值发生的概率.
学习新知
例2.一批产品中次品率为5%,随机抽取1件,定义X,
解:根据
X 0 1
P 0.95 0.05
学习新知
X 0 1
P 1-P P
对于只有两个可能结果的随机试验,用 表示“成功”,表示“失败”,定义
学习新知
学习新知
归纳提高
巩固提升
求离散型随机变量分布列时应注意的问题
(1)确定离散型随机变量 X 的分布列的关键是要清楚 X 取每一个值对应的随机事件,进一步利用排列、组合知识求出 X 取每一个值的概率.
(2)在求离散型随机变量 X 的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可以验证分布列是否正确.
归纳提高
谢谢观看!
7.2 离散型随机变量及其分布
2
学习目标
1.理解随机变量的意义,了解随机变量与函数的区别;
2.掌握离散型随机变量的概念,能够写出随机变量的取值以及随机试验的结果;
3.理解取有限值的离散型随机变量的分布列及两点分布的概念及表示.
4.掌握离散型随机变量的分布列的性质.
5.会求某些简单的离散型随机变量的分布列(含两点分布).
1. 随机试验
一般地,一个试验如果满足下列条件:
①试验可以在相同的情形下重复进行;
②试验的所有可能结果是明确可知的,并且不只一个;
③每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前却不能肯定这次试验
会出现哪一个结果; 这种试验就是一个随机试验,为了方便起见,也简称试验.
2. 函数
一般地,设A,B是非空的数集,如果使对于集合A中的任意一个数x ,按照某种确定的对应关系f ,在集合B中都有唯一确定的数 y 和它对应,那么就称f :A→B为从集合A到集合B的一个函数,记作:
随机试验的样本空间与实数集之间能否建立某种对应关系呢?
知识回顾
数学活动1
探究1.有些随机试验的样本空间与数值有关系,我们可以直接与实数建立关系.
(1)掷一枚骰子用实数 ( =1,2,3,4,5,6)表示“掷出的点数为 ”,又如,掷两枚骰子样本空间为Ω={ ( , ) | , =1,2, 6},用 + 表示“两枚骰子的点数之和”样本点( , )就与实数 + 对应.
(2)某射击运动员在射击训练中,其中某次射击可能出现命中的环数情况有哪些?
实数 ( =0,1,2,3,4,5,6,···,10)表示“击中环数 ”
(0环、1环、2环、···、10环)共11种结果
探究2. 考察下列随机试验及其引入的变量:
试验1: 从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验,变量X 表示三个元件中次品数;
试验2: 抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么 各个样本点与变量的值是如何对应的
数学活动1
数学活动1
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验,变量X 表示三个元件中次品数;用0表示“元件为合格品”,1表示“元件为次品”,
用0和1构成的长度为3的字符串表示样本点,则
样本空间Ω1={000,001,010,100,011,101,110,111},
试验2:抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
变量X,Y 有哪些共同的特征
学习新知
1.随机变量的定义
2.离散型随机变量的定义
随机变量的特点
可以用数字表示
试验之前可以判断其可能出现的所有值
在试验之前不可能确定取何值
随机变量将随机事件的结果数量化.
例1.写出下列各随机变量可能的取值,并说明随机变量所取值所表示的随机试验的结果:
(1)从10张已编号的卡片(从1号到10号)中任取1张,被取出的卡片的号数X 。
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球数X.
(3)抛掷两个骰子,所得点数之和X.
(4)某射击运动员射击一次可能命中的环数X .
(5)某一自动装置无故障运转的时间X.
(6)某林场树木最高达30米,此林场树木的高度X .
解:(1)X =1、2、3、···、10;(2)X=0、1、2、3;
(3)X=2、3、4、···、12;(4) X=0、1、2、3、···、10;
(5) X取内的一切值;(6)X取内的一切值.
学习新知
学习新知
学习新知
思考1.下列变量中是离散型随机变量的是?
(1)下期《诗词大会》节目中过关的人数;
(2)某加工厂加工的一批某种钢管的外径与规定的外径尺寸之差;
(3)在郑州至武汉的电气化铁道线上,每隔50 m有一电线铁塔,从郑州至武汉的电气化铁道线上将电线铁塔进行编号,其中某一电线铁塔的编号;
(4)江西九江市长江水位监测站所测水位在(0,29]这一范围内变化,该水位站所测水位.
答案:(1)(3)
变式探究: 将本题的(4)改为:监测站所测水位X是否超过警戒水位(警戒水位是29 m),X是离散型随机变量吗
12
学习新知
解析式法:P(X=xi)= pi , i=1,2,3…,n
图象法:
2. 函数可以用解析式、表格、图象表示。离散型随机变量的分布列也可以用解析式、表格、图象表示。
X x1 x2 … xk … xn
P p1 p2 … pk … pn
表格法:
学习新知
3.离散型随机变量的分布列具有下述两个性质:
注意:① 列出随机变量的所有可能取值;
② 求出随机变量的每一个值发生的概率.
学习新知
例2.一批产品中次品率为5%,随机抽取1件,定义X,
解:根据
X 0 1
P 0.95 0.05
学习新知
X 0 1
P 1-P P
对于只有两个可能结果的随机试验,用 表示“成功”,表示“失败”,定义
学习新知
学习新知
归纳提高
巩固提升
求离散型随机变量分布列时应注意的问题
(1)确定离散型随机变量 X 的分布列的关键是要清楚 X 取每一个值对应的随机事件,进一步利用排列、组合知识求出 X 取每一个值的概率.
(2)在求离散型随机变量 X 的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可以验证分布列是否正确.
归纳提高
谢谢观看!
