数学人教A版(2019)选择性必修第三册7.1.1条件概率(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.1.1条件概率(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 656.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 23:03:46 | ||
图片预览





文档简介
(共19张PPT)
7.1.1 条件概率
情 境 引 入
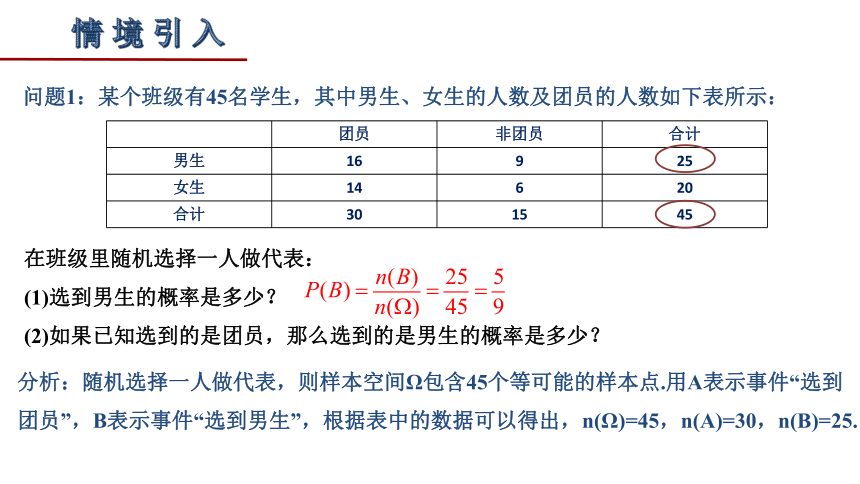
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
分析:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.用A表示事件“选到团员”,B表示事件“选到男生”,根据表中的数据可以得出,n(Ω)=45,n(A)=30,n(B)=25.
情 境 引 入
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:
“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为 P(B|A). 此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
分析:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.用A表示事件“选到团员”,
B表示事件“选到男生”,根据表中的数据可以得出,n(Ω)=45,n(A)=30,n(B)=25.
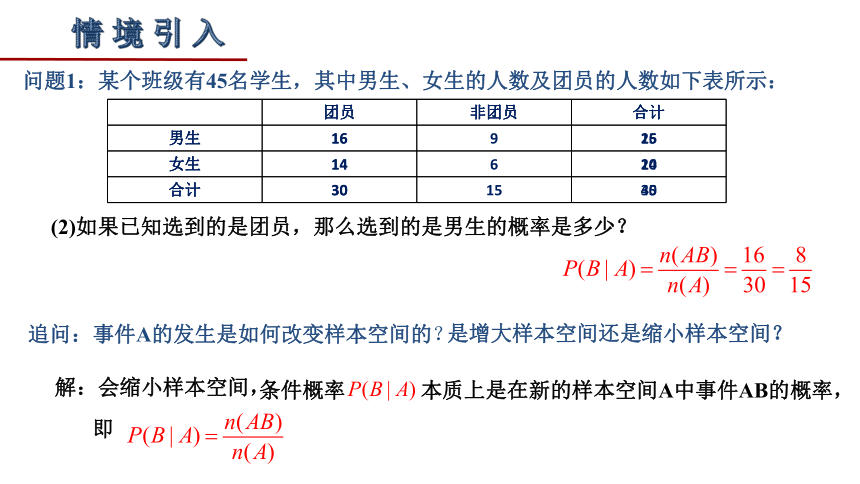
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
情 境 引 入
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 16
女生 14 14
合计 30 30
追问:事件A的发生是如何改变样本空间的?
是增大样本空间还是缩小样本空间?
条件概率 本质上是在新的样本空间A中事件AB的概率,
即
解:会缩小样本空间,
样本空间 ,且所有的样本点都是等可能的.
情 境 引 入
解:如果b表示男孩,g表示女孩,问题2满足古典概型的条件.
“在选择的家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A). 此时A成为样本空间,事件B就是积事件AB.
根据古典概型知识可知,
问题2:假定生男孩生女孩是等可能的,现在考虑有两个小孩的家庭.随机选择一个家庭,
那么(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又有多大?
设 A=“选择的家庭中有女孩”,则
设 B=“选择的家庭中有两个小孩都是女孩”,则
(1) 根据古典概型知识可知,该家庭中两个小孩都是女孩的概率是
[思考]
情 境 引 入
通过问题1和问题2,你能得到什么结论?
与 , ,
[问题3]
结合以上两个问题,你能探索条件概率
之间的关系吗?
对于一般的古典概型,在事件A发生的条件下,事件B发生的概率都是
借助Venn图可知,
A
B
AB
若已知事件A发生,则A成为样本空间.
此时B发生的概率是AB包含样本点数与A包含样本点数的比值,即 .
因为
所以在事件A发生的条件下,事件B发生的概率可以通过 来计算
一般地,设A,B为两个事件, 且P(A)>0, 称
为在事件A发生的条件下,事件B发生的条件概率.
一般把 P(B|A)读作 A 发生的条件下 B 发生的概率.
抽 象 概 念
定义:
反之,若P(B|A)=P(B),且P(A)>0,则:
精 微 概 念
条件概率与事件独立性的关系
在问题1和问题2中,都有P(B|A)≠P(B). 一般地, P(B|A)与P(B)不一定相等.如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件?为什么?
直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,这等价于P(B|A)=P(B)成立.
[追问]对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B|A),
称此式为概率的乘法公式.
[问题4]
事实上,若事件A与B相互独立,即P(AB)=P(A)P(B),且P(A)>0,则:
P(AB)=P(A)P(B)
因此,当P(A)>0时,当且仅当A与B相互独立时,有
P(B|A)=P(B)
例1:在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不
再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是
积事件的概率,问题(2)就是条件概率. 可以先求积事件的概率,再用条件概率公式求条
件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
应 用 新 知
条件概率、乘法公式的应用
<解法一>:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取
2道,试验的样本空间Ω包含20个等可能的样本点,即 ,
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件
B发生的概率.显然 .利用条件概率公式,得
例1:在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不
再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是
积事件的概率,问题(2)就是条件概率. 可以先求积事件的概率,再用条件概率公式求条
件概率; 也可以先求条件概率,再用乘法公式求积事件的概率.
应 用 新 知
条件概率、乘法公式的应用
<解法二>:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,这时还余下4道试题,其中代数题和几何题各2道. 因此,事件A发生的条件下,事件B发生的概率为
利用乘法公式可得
掷两颗均匀骰子,问:
⑴“第一颗掷出6点”的概率是多少?
⑵ “掷出点数之和不小于10”的概率又是多少
⑶ “已知第一颗掷出6点,则掷出点数之和不小于10”的概率呢?
【变式练习】
应 用 新 知
11 12 13 14 15 16
21 22 23 24 25 26
31 32 33 34 35 36
41 42 43 44 45 46
51 52 53 54 55 56
61 62 63 64 65 66
61 62 63 64 65 66
解:设Ω为所有基本事件组成的全体,“第一颗掷出6点”为事件A,“掷出点数之和
不小于10”为事件B,则“已知第一颗掷出6点,掷出点数之和不小于10”为事件AB.
应 用 新 知
[问题5]通过以上的例题解答,请问求条件概率一般有几种方法?你认为条件概率有什么性质?
引 出 性 质
计算A发生的条件下事件B发生的条件概率的两种方法:
(通常适用古典概率模型)
(适用于一般的概率模型)
一种是基于样本空间 ,先计算P(A)和P(AB),再利用条件概率公式求P(B|A).
另一种是根据条件概率的直观意义,增加了“A发生”的条件后,样本空间
缩小为A,求P(B|A)就是以A为样本空间计算AB的概率.
[问题5]通过以上的例题解答,请问求条件概率一般有几种方法?你认为条件概率有什么性质?
引 出 性 质
条件概率只是缩小了样本空间,因此条件概率同样具有概率的性质.
设 P(A)>0,则
如果B和C是两个互斥事件,则
设B和 互为对立事件,则
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各
随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
:用A,B,C分别表示甲、乙、丙中奖的事件,则B=.
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关。
应 用 新 知
A
B
C
[追问]若是放回随机抽样,中奖的概率与抽奖的次序有关吗?获奖的情况会有什么改变
无论是放回或不放回,中奖的概率都与抽奖的次序无关,都是
析
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记
了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:(1)设Ai=“第i次按对密码”(i=1,2),
则事件“不超过2次就按对密码”等价于“第一次按对,或者第一次按错但第
二次按对”可表示为A=A1UA2).
事件A1与事件A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P(A2)= P(A1)+P()P(A2|)=
因此,任意按最后1位数字,不超过2次就按对的概率为.
(2)设B=“最后1位密码为偶数”,则P(A|B)=P(A1|B)+P(A2|B)==;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
应 用 新 知
1. 什么是条件概率?条件概率与积事件的概率有什么关系?
2. 对于随机事件A、B,请你说一说“事件A、B同时发生”与“在事件A发生的条
件下,事件B发生”的区别,这两个事件的概率有什么关系?哪个概率更大?
3. 求条件概率一般有几种方法?
(1)减缩样本空间法
(2)条件概率定义法
总 结 提 升
4. 条件概率有哪些性质?
布 置 作 业
教科书第48页练习1、2题,
习题7.1第1、2、3、6、9、10题
再见
7.1.1 条件概率
情 境 引 入
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
分析:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.用A表示事件“选到团员”,B表示事件“选到男生”,根据表中的数据可以得出,n(Ω)=45,n(A)=30,n(B)=25.
情 境 引 入
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:
“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为 P(B|A). 此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
分析:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.用A表示事件“选到团员”,
B表示事件“选到男生”,根据表中的数据可以得出,n(Ω)=45,n(A)=30,n(B)=25.
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
情 境 引 入
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示:
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 16
女生 14 14
合计 30 30
追问:事件A的发生是如何改变样本空间的?
是增大样本空间还是缩小样本空间?
条件概率 本质上是在新的样本空间A中事件AB的概率,
即
解:会缩小样本空间,
样本空间 ,且所有的样本点都是等可能的.
情 境 引 入
解:如果b表示男孩,g表示女孩,问题2满足古典概型的条件.
“在选择的家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A). 此时A成为样本空间,事件B就是积事件AB.
根据古典概型知识可知,
问题2:假定生男孩生女孩是等可能的,现在考虑有两个小孩的家庭.随机选择一个家庭,
那么(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又有多大?
设 A=“选择的家庭中有女孩”,则
设 B=“选择的家庭中有两个小孩都是女孩”,则
(1) 根据古典概型知识可知,该家庭中两个小孩都是女孩的概率是
[思考]
情 境 引 入
通过问题1和问题2,你能得到什么结论?
与 , ,
[问题3]
结合以上两个问题,你能探索条件概率
之间的关系吗?
对于一般的古典概型,在事件A发生的条件下,事件B发生的概率都是
借助Venn图可知,
A
B
AB
若已知事件A发生,则A成为样本空间.
此时B发生的概率是AB包含样本点数与A包含样本点数的比值,即 .
因为
所以在事件A发生的条件下,事件B发生的概率可以通过 来计算
一般地,设A,B为两个事件, 且P(A)>0, 称
为在事件A发生的条件下,事件B发生的条件概率.
一般把 P(B|A)读作 A 发生的条件下 B 发生的概率.
抽 象 概 念
定义:
反之,若P(B|A)=P(B),且P(A)>0,则:
精 微 概 念
条件概率与事件独立性的关系
在问题1和问题2中,都有P(B|A)≠P(B). 一般地, P(B|A)与P(B)不一定相等.如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件?为什么?
直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,这等价于P(B|A)=P(B)成立.
[追问]对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B|A),
称此式为概率的乘法公式.
[问题4]
事实上,若事件A与B相互独立,即P(AB)=P(A)P(B),且P(A)>0,则:
P(AB)=P(A)P(B)
因此,当P(A)>0时,当且仅当A与B相互独立时,有
P(B|A)=P(B)
例1:在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不
再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是
积事件的概率,问题(2)就是条件概率. 可以先求积事件的概率,再用条件概率公式求条
件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
应 用 新 知
条件概率、乘法公式的应用
<解法一>:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取
2道,试验的样本空间Ω包含20个等可能的样本点,即 ,
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件
B发生的概率.显然 .利用条件概率公式,得
例1:在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不
再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是
积事件的概率,问题(2)就是条件概率. 可以先求积事件的概率,再用条件概率公式求条
件概率; 也可以先求条件概率,再用乘法公式求积事件的概率.
应 用 新 知
条件概率、乘法公式的应用
<解法二>:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,这时还余下4道试题,其中代数题和几何题各2道. 因此,事件A发生的条件下,事件B发生的概率为
利用乘法公式可得
掷两颗均匀骰子,问:
⑴“第一颗掷出6点”的概率是多少?
⑵ “掷出点数之和不小于10”的概率又是多少
⑶ “已知第一颗掷出6点,则掷出点数之和不小于10”的概率呢?
【变式练习】
应 用 新 知
11 12 13 14 15 16
21 22 23 24 25 26
31 32 33 34 35 36
41 42 43 44 45 46
51 52 53 54 55 56
61 62 63 64 65 66
61 62 63 64 65 66
解:设Ω为所有基本事件组成的全体,“第一颗掷出6点”为事件A,“掷出点数之和
不小于10”为事件B,则“已知第一颗掷出6点,掷出点数之和不小于10”为事件AB.
应 用 新 知
[问题5]通过以上的例题解答,请问求条件概率一般有几种方法?你认为条件概率有什么性质?
引 出 性 质
计算A发生的条件下事件B发生的条件概率的两种方法:
(通常适用古典概率模型)
(适用于一般的概率模型)
一种是基于样本空间 ,先计算P(A)和P(AB),再利用条件概率公式求P(B|A).
另一种是根据条件概率的直观意义,增加了“A发生”的条件后,样本空间
缩小为A,求P(B|A)就是以A为样本空间计算AB的概率.
[问题5]通过以上的例题解答,请问求条件概率一般有几种方法?你认为条件概率有什么性质?
引 出 性 质
条件概率只是缩小了样本空间,因此条件概率同样具有概率的性质.
设 P(A)>0,则
如果B和C是两个互斥事件,则
设B和 互为对立事件,则
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各
随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
:用A,B,C分别表示甲、乙、丙中奖的事件,则B=.
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关。
应 用 新 知
A
B
C
[追问]若是放回随机抽样,中奖的概率与抽奖的次序有关吗?获奖的情况会有什么改变
无论是放回或不放回,中奖的概率都与抽奖的次序无关,都是
析
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记
了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:(1)设Ai=“第i次按对密码”(i=1,2),
则事件“不超过2次就按对密码”等价于“第一次按对,或者第一次按错但第
二次按对”可表示为A=A1UA2).
事件A1与事件A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P(A2)= P(A1)+P()P(A2|)=
因此,任意按最后1位数字,不超过2次就按对的概率为.
(2)设B=“最后1位密码为偶数”,则P(A|B)=P(A1|B)+P(A2|B)==;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
应 用 新 知
1. 什么是条件概率?条件概率与积事件的概率有什么关系?
2. 对于随机事件A、B,请你说一说“事件A、B同时发生”与“在事件A发生的条
件下,事件B发生”的区别,这两个事件的概率有什么关系?哪个概率更大?
3. 求条件概率一般有几种方法?
(1)减缩样本空间法
(2)条件概率定义法
总 结 提 升
4. 条件概率有哪些性质?
布 置 作 业
教科书第48页练习1、2题,
习题7.1第1、2、3、6、9、10题
再见
