6.1圆周运动(共14张ppt)
文档属性
| 名称 | 6.1圆周运动(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-25 20:14:09 | ||
图片预览




文档简介
(共14张PPT)
6.1 圆周运动
第六章 圆周运动
必备知识:知道什么是圆周运动,什么是匀速圆周运动
关键能力:1、理解什么是线速度、角速度
2、掌握线速度和角速度的关系
3、了解转速和周期与线速度和角速度的关系
学科素养:能在具体情境中应用线速度、角速度、转速、
周期的关系解决相关实际问题
学习目标
在物理学中,把质点的运动轨迹是圆或圆弧的一部分的运动叫做圆周运动
情境引入
如图1所示,自行车在行进过程中,大齿轮、小齿轮和车后轮是相互关联的三个转动部分,它们在同时转动。
思考:如图2,后轮上有两点A(绿)和B(红)
1、两点做什么运动?有什么特点?
2、两点速度方向沿什么方向?
图1
图2
3、如果A点在任意相等的时间内转过的弧长相等,A点做匀速运动么?
4、两点运动的快慢一样么?如何判断?
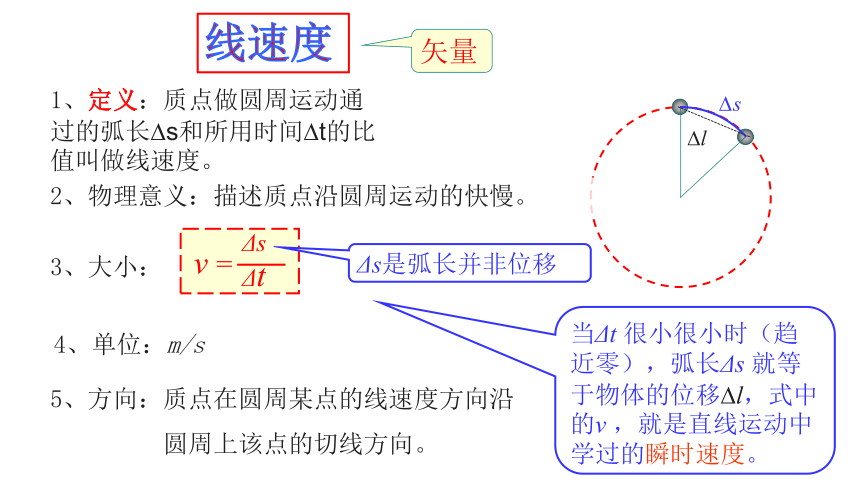
2、物理意义:描述质点沿圆周运动的快慢。
1、定义:质点做圆周运动通过的弧长Ds和所用时间Dt的比值叫做线速度。
3、大小:
4、单位:m/s
v =
Δt
Δs
5、方向:质点在圆周某点的线速度方向沿
圆周上该点的切线方向。
Δs是弧长并非位移
当Δt 很小很小时(趋近零),弧长Δs 就等于物体的位移Dl,式中的v ,就是直线运动中学过的瞬时速度。
矢量
s
Dl
线速度
v
v
v
o
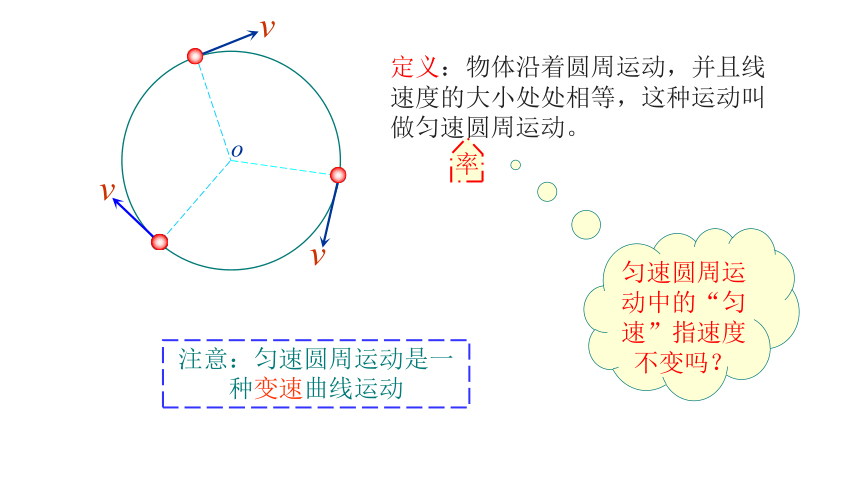
定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
率
匀速圆周运动中的“匀速”指速度不变吗?
注意:匀速圆周运动是一 种变速曲线运动
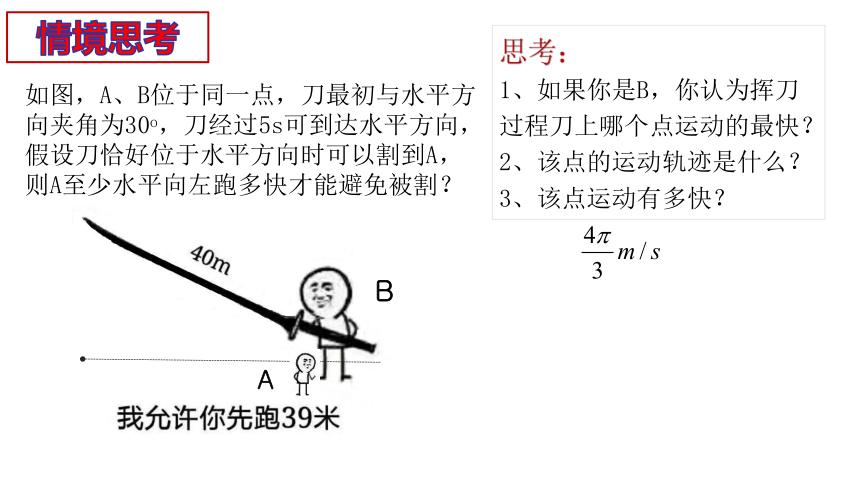
思考:
1、如果你是B,你认为挥刀过程刀上哪个点运动的最快?
2、该点的运动轨迹是什么?
3、该点运动有多快?
如图,A、B位于同一点,刀最初与水平方向夹角为30o,刀经过5s可到达水平方向,假设刀恰好位于水平方向时可以割到A,则A至少水平向左跑多快才能避免被割?
情境思考
A
B
1、挥刀过程中,刀上各点绕刀把转过的角度相同么?
2、刀上各点绕刀把转动快慢相同么?
3、尝试求解刀转动的角速度大小?
问题引导
B
引入角速度概念
2、物理意义:描述质点绕圆心转动的快慢。
1、定义:质点所在的半径转过圆心角Δθ和所用时间Δt的比值叫做角速度。
3、大小:
4、单位:rad/s
ω=
Δt
Δ
θ
Δ
θ
Δθ采用弧度制
说明:匀速圆周运动是角速度不变的运动。
角速度
矢量
周期 频率 转速
定义
符号
单位
物理意义
关系
n
r/s或r/min
描述物体做圆周运动的快慢
物体运动一周所用的时间
T
s
Hz或s-1
n = f =
T
1
物体在单位时间所转过的圈数
f
物体在单位时间所转过的圈数
匀速圆周运动是周期、频率、转速都不变的运动!
圆周运动其他物理量
设物体做半径为 r 的匀速圆周运动,半径为r
v =
T
2πr
线速度与周期的关系:
角速度与周期的关系:
ω=
T
2π
线速度、角速度与周期之间有什么关系?
r
v = rω
线速度与角速度的关系(思路一):
线速度与角速度的关系(思路2)
设物体做半径为r的圆周运动,在Δt内通过的弧长为Δs,半径转过的角度为Δθ
由数学知识得Δs = rΔθ
v = rω
s
Δ
θ
r
等式两边同时除以时间
得:
例题:两个小球固定在一根长为L的杆的两端,绕杆上的O点做圆周运动,如图所示,当小球1的速度为v1时,小球2的速度为v2 ,以下说法不正确的是( )
A.小球1距离O点的距离为
B.小球2距离O点的距离为
C.小球1的角速度为
D.小球1和小球2的线速度和角速度均相同
v1
v2
O
D
1、圆周运动的概念
3、匀速圆周运动的特点及性质
2、描述圆周运动的几个物理量及其关系
v =
T
2πr
ω=
T
2π
v = rω
v =
Δt
Δl
ω=
Δt
Δ
θ
n = f =
T
1
(1)、线速度大小不变,方向时刻变化,是变速运动
(2)、速率、角速度、周期、频率、转速都不变
小结
6.1 圆周运动
第六章 圆周运动
必备知识:知道什么是圆周运动,什么是匀速圆周运动
关键能力:1、理解什么是线速度、角速度
2、掌握线速度和角速度的关系
3、了解转速和周期与线速度和角速度的关系
学科素养:能在具体情境中应用线速度、角速度、转速、
周期的关系解决相关实际问题
学习目标
在物理学中,把质点的运动轨迹是圆或圆弧的一部分的运动叫做圆周运动
情境引入
如图1所示,自行车在行进过程中,大齿轮、小齿轮和车后轮是相互关联的三个转动部分,它们在同时转动。
思考:如图2,后轮上有两点A(绿)和B(红)
1、两点做什么运动?有什么特点?
2、两点速度方向沿什么方向?
图1
图2
3、如果A点在任意相等的时间内转过的弧长相等,A点做匀速运动么?
4、两点运动的快慢一样么?如何判断?
2、物理意义:描述质点沿圆周运动的快慢。
1、定义:质点做圆周运动通过的弧长Ds和所用时间Dt的比值叫做线速度。
3、大小:
4、单位:m/s
v =
Δt
Δs
5、方向:质点在圆周某点的线速度方向沿
圆周上该点的切线方向。
Δs是弧长并非位移
当Δt 很小很小时(趋近零),弧长Δs 就等于物体的位移Dl,式中的v ,就是直线运动中学过的瞬时速度。
矢量
s
Dl
线速度
v
v
v
o
定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
率
匀速圆周运动中的“匀速”指速度不变吗?
注意:匀速圆周运动是一 种变速曲线运动
思考:
1、如果你是B,你认为挥刀过程刀上哪个点运动的最快?
2、该点的运动轨迹是什么?
3、该点运动有多快?
如图,A、B位于同一点,刀最初与水平方向夹角为30o,刀经过5s可到达水平方向,假设刀恰好位于水平方向时可以割到A,则A至少水平向左跑多快才能避免被割?
情境思考
A
B
1、挥刀过程中,刀上各点绕刀把转过的角度相同么?
2、刀上各点绕刀把转动快慢相同么?
3、尝试求解刀转动的角速度大小?
问题引导
B
引入角速度概念
2、物理意义:描述质点绕圆心转动的快慢。
1、定义:质点所在的半径转过圆心角Δθ和所用时间Δt的比值叫做角速度。
3、大小:
4、单位:rad/s
ω=
Δt
Δ
θ
Δ
θ
Δθ采用弧度制
说明:匀速圆周运动是角速度不变的运动。
角速度
矢量
周期 频率 转速
定义
符号
单位
物理意义
关系
n
r/s或r/min
描述物体做圆周运动的快慢
物体运动一周所用的时间
T
s
Hz或s-1
n = f =
T
1
物体在单位时间所转过的圈数
f
物体在单位时间所转过的圈数
匀速圆周运动是周期、频率、转速都不变的运动!
圆周运动其他物理量
设物体做半径为 r 的匀速圆周运动,半径为r
v =
T
2πr
线速度与周期的关系:
角速度与周期的关系:
ω=
T
2π
线速度、角速度与周期之间有什么关系?
r
v = rω
线速度与角速度的关系(思路一):
线速度与角速度的关系(思路2)
设物体做半径为r的圆周运动,在Δt内通过的弧长为Δs,半径转过的角度为Δθ
由数学知识得Δs = rΔθ
v = rω
s
Δ
θ
r
等式两边同时除以时间
得:
例题:两个小球固定在一根长为L的杆的两端,绕杆上的O点做圆周运动,如图所示,当小球1的速度为v1时,小球2的速度为v2 ,以下说法不正确的是( )
A.小球1距离O点的距离为
B.小球2距离O点的距离为
C.小球1的角速度为
D.小球1和小球2的线速度和角速度均相同
v1
v2
O
D
1、圆周运动的概念
3、匀速圆周运动的特点及性质
2、描述圆周运动的几个物理量及其关系
v =
T
2πr
ω=
T
2π
v = rω
v =
Δt
Δl
ω=
Δt
Δ
θ
n = f =
T
1
(1)、线速度大小不变,方向时刻变化,是变速运动
(2)、速率、角速度、周期、频率、转速都不变
小结
