初中数学苏科版九年级上册 1.4数的开方 课件(共21张)
文档属性
| 名称 | 初中数学苏科版九年级上册 1.4数的开方 课件(共21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 789.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
1.4 数的开方
数学是思维的体操。
——培根
知识点1 二次根式的概念与性质
1. 概念:一般地,我们把形如 的式子叫做二次根式.
2. 使二次根式有意义的条件:
(1) 被开方数 ;
(2) 若根式在分母中出现,则被开方数大于 .
3. 最简二次根式:
(1) 被开方数不含 ;
(2) 被开方数中不含 的因数或因式.
4. 二次根式的性质:
(1) 二次根式(a≥0)是一个 数;
(2) ()2= (a≥0);
(3) =||=
(≥0)
是非负数
0
分母
能开得尽方
非负
知识点2 二次根式的运算
1. 乘法法则:·= (a≥0,b≥0).
2. 除法法则:= (a≥0,b>0).
3. 二次根式的加减:先把各个二次根式化成 ,再把
相同的二次根式进行合并.
4. 分母有理化:
(1) ==(a>0);
(2) ==(≠±b,a≥0).
5. 二次根式的运算顺序与 的运算顺序一样,先乘方、开方,再
乘除,最后加减,有括号的先算括号内的.
最简二次根式
被开方数
实数
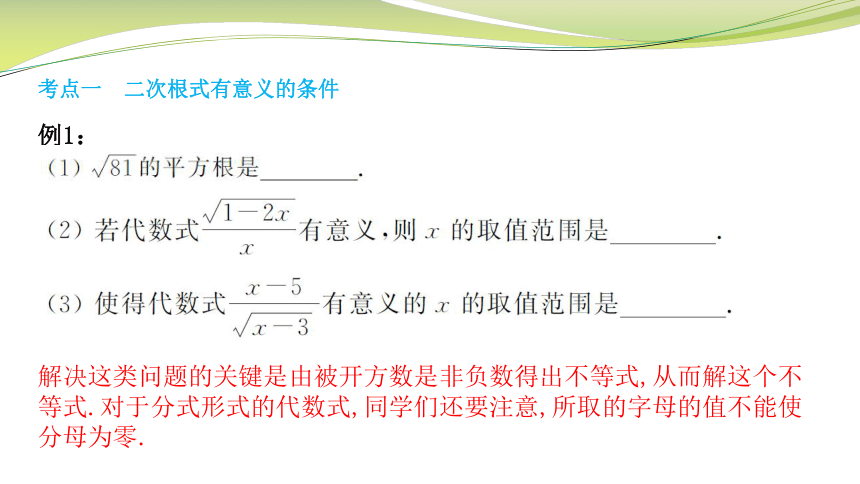
例1:
考点一 二次根式有意义的条件
解决这类问题的关键是由被开方数是非负数得出不等式,从而解这个不等式.对于分式形式的代数式,同学们还要注意,所取的字母的值不能使分母为零.
反馈1:
例2:
例2:
考点二 二次根式的计算
理解二次根式的性质与相关运算法则是解题的关键,如=|a|,(a)2=a2b(b≥0),另外当二次根式化简为最简二次根式后,被开方数相同时才能进行二次根式的加减.
反馈2:
反馈2:
反馈2:
例3:
考点三 二次根式的性质和最简二次根式
例3:
考点四 二次根式在分式运算中的应用
例4:先化简,再求值:(-)÷,其中a=+1,b=-1.
1、二次根式的概念与性质:双重非负性及根号里外非负
2、二次根式的计算:先乘除,再化最简根式,后加减合并同类根式
3、分式的运算与二次根式的求值相结合时,先化简分式(或整式),然后将相关值代入,最后利用二次根式的运算法则解决问题.
小结
In maths,“what” is not important ,
only “how” is .
———毕达哥拉斯
在数学领域中,知道什么不重要,
重要的是要知道怎样来的
谢 谢!
1. 下列各式中,属于最简二次根式的为 ( )
A. B. C. D.
2. 下列实数中,属于有理数的是 ( )
A. B. C. D.
3. 下列计算中,正确的是 ( )
A. 5-2=21 B. 2+=2
C. ×=3 D. ÷=3
4. 若x=+1,则代数式x2-2x+2的值为 ( )
A. 7 B. 4 C. 3 D. 3-2
A
C
C
C
课后检测
5. 若式子在实数范围内有意义,则x的取值范围是 .
6. 计算-2的结果是 .
7. 计算-×的结果是 .
8. 计算(+1)(-1)的结果是 .
x≥0
2
-
9
9. 计算:
(1) (-)(+)-|-3|-(-1)2021;
(2) -(-)÷+tan30°;
(3) (-π)0++-2cos45°.
(1) 2+
(2) 2
(3) 2
10. 先化简,再求值:
(1) ÷,其中a=-1;
(2) ÷,其中a=2;
(3)÷,其中x=,y=1.
(1) 原式=.当a=-1时,原式=
(2) 原式=.当a=2时,原式==
(3) 原式=.当x=,y=1时,原式=4+4
1.4 数的开方
数学是思维的体操。
——培根
知识点1 二次根式的概念与性质
1. 概念:一般地,我们把形如 的式子叫做二次根式.
2. 使二次根式有意义的条件:
(1) 被开方数 ;
(2) 若根式在分母中出现,则被开方数大于 .
3. 最简二次根式:
(1) 被开方数不含 ;
(2) 被开方数中不含 的因数或因式.
4. 二次根式的性质:
(1) 二次根式(a≥0)是一个 数;
(2) ()2= (a≥0);
(3) =||=
(≥0)
是非负数
0
分母
能开得尽方
非负
知识点2 二次根式的运算
1. 乘法法则:·= (a≥0,b≥0).
2. 除法法则:= (a≥0,b>0).
3. 二次根式的加减:先把各个二次根式化成 ,再把
相同的二次根式进行合并.
4. 分母有理化:
(1) ==(a>0);
(2) ==(≠±b,a≥0).
5. 二次根式的运算顺序与 的运算顺序一样,先乘方、开方,再
乘除,最后加减,有括号的先算括号内的.
最简二次根式
被开方数
实数
例1:
考点一 二次根式有意义的条件
解决这类问题的关键是由被开方数是非负数得出不等式,从而解这个不等式.对于分式形式的代数式,同学们还要注意,所取的字母的值不能使分母为零.
反馈1:
例2:
例2:
考点二 二次根式的计算
理解二次根式的性质与相关运算法则是解题的关键,如=|a|,(a)2=a2b(b≥0),另外当二次根式化简为最简二次根式后,被开方数相同时才能进行二次根式的加减.
反馈2:
反馈2:
反馈2:
例3:
考点三 二次根式的性质和最简二次根式
例3:
考点四 二次根式在分式运算中的应用
例4:先化简,再求值:(-)÷,其中a=+1,b=-1.
1、二次根式的概念与性质:双重非负性及根号里外非负
2、二次根式的计算:先乘除,再化最简根式,后加减合并同类根式
3、分式的运算与二次根式的求值相结合时,先化简分式(或整式),然后将相关值代入,最后利用二次根式的运算法则解决问题.
小结
In maths,“what” is not important ,
only “how” is .
———毕达哥拉斯
在数学领域中,知道什么不重要,
重要的是要知道怎样来的
谢 谢!
1. 下列各式中,属于最简二次根式的为 ( )
A. B. C. D.
2. 下列实数中,属于有理数的是 ( )
A. B. C. D.
3. 下列计算中,正确的是 ( )
A. 5-2=21 B. 2+=2
C. ×=3 D. ÷=3
4. 若x=+1,则代数式x2-2x+2的值为 ( )
A. 7 B. 4 C. 3 D. 3-2
A
C
C
C
课后检测
5. 若式子在实数范围内有意义,则x的取值范围是 .
6. 计算-2的结果是 .
7. 计算-×的结果是 .
8. 计算(+1)(-1)的结果是 .
x≥0
2
-
9
9. 计算:
(1) (-)(+)-|-3|-(-1)2021;
(2) -(-)÷+tan30°;
(3) (-π)0++-2cos45°.
(1) 2+
(2) 2
(3) 2
10. 先化简,再求值:
(1) ÷,其中a=-1;
(2) ÷,其中a=2;
(3)÷,其中x=,y=1.
(1) 原式=.当a=-1时,原式=
(2) 原式=.当a=2时,原式==
(3) 原式=.当x=,y=1时,原式=4+4
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
