2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.4组合数 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.4组合数 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 778.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
6.2.4 组合数
一、温故知新
问题1 从集合中取出3个元素组成三元子集,共有
哪些不同的子集?
二、新知探究
组合数概念:从个不同元素中取出个元素的所有不同组合的个数,叫做从个不同元素中取出个元素的组合数,记作。
例如,从4个不同元素中取出3个元素的组合数表示为
组合与组合数的区别:
组合数是一个非零自然数
组合不是一个数字
问题2 前面已经提到,组合和排列有关系,我们能否利用这种关系,
由排列数来求组合数呢?
二、新知探究
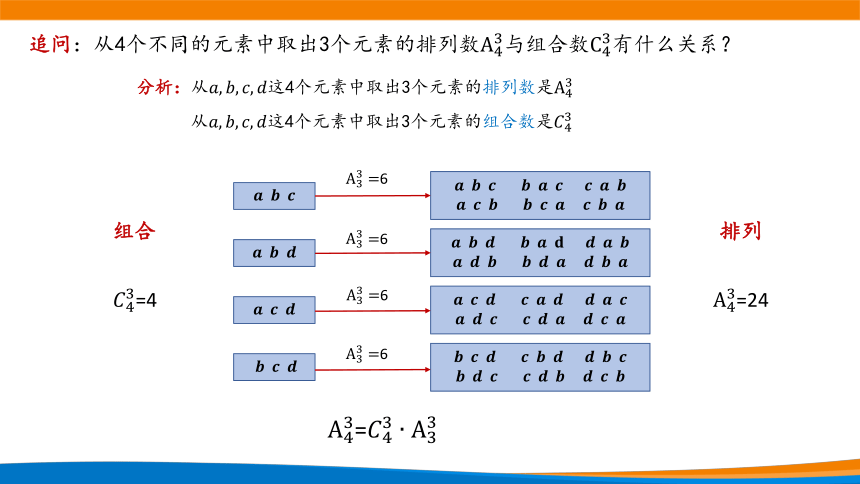
追问:从4个不同的元素中取出3个元素的排列数与组合数有什么关系?
分析:从这4个元素中取出3个元素的排列数是
从这4个元素中取出3个元素的组合数是
组合
排列
=4
6
=24
6
6
6
=
=
左式 从4个元素中取出3个元素的排列数
右式 第1步:从4个元素中取出3个元素作为一组,共有种取法
第2步:将取出的3个元素作全排列,共有种排法
根据分步乘法计数原理,有,即
=4
一般地,求“从个不同元素中任取个元素的排列数”,可以由以下两步得到:
第1步:从个不同元素中任取个元素作为一组,共有种不同的取法;
第2步:将取出的个元素作全排列,共有种不同的排法。
根据分步乘法计数原理,有,因此
追问(2):由的公式,你能得到的公式吗?
连乘形式
阶乘形式
组合数公式:
规定:
三、学以致用
例1 计算:(1) (2) (3) (4)
解:根据组合数公式,可得
(1)
(2)
(3)
(4)
追问:观察(1)与(2),(3)与(4)的结果,你有什么发现和猜想?
,
特征:两个组合数的下标相同,上标相加等于下标
猜想
证明:
方法1:组合数的意义
方法2:组合数的计算
取出个元素的组合 留下个元素的组合
“一一对应”
所以等式成立
组合数的性质1:
(1)反映了组合数的对称性
(2)当时,可以将计算转化为计算,有助于简化运算
例2:一个口袋里有7个不同的白球和1个红球,从中取出5个球:
(1)共有多少种不同的取法?
(2)如果必须取红球,共有多少种不同的取法?
解:(1)从8个球中取出5个,是一个组合问题,方法数为
。
(2)红球只有1个,问题转化为“从7个白球中取出4个”,也是一个组合问题,
有 种取法。
56
例2 一个口袋里有7个不同的白球和1个红球,从中取出5个球:
(3)如果不取红球,共有多少种不同的取法?
(3)方法1:问题转化为“从7个不同白球中取出5个白球”,
故有种取法。
方法2:“不取红球”的反面是必须取红球,
从“任意取出5个球”中,去掉“必须取红球”即可
有种取法
直接法
间接法
追问:你能解释 的意义吗?
分析:一个口袋里有7个不同的白球和1个红球,从中取出5个球
左式 从8个元素中任取5个,共有种取法
根据分类加法计数原理,
猜想:
右式 第1类:不含特殊元素(红球),共有种取法;
第2类:含有特殊元素(红球),共有种取法
证明:
方法1:从组合数的意义
(从含有1个特殊元素的个元素中任取个的组合)
左式 从(个元素中任取个,共有种取法
右式 第1类:不含特殊元素,共有种取法;
第2类:含有特殊元素,共有种取法
根据分类加法计数原理,
方法2:从组合数的计算(课后作业)
组合数的性质2:
(1)特征:下标相同,上标相差1的两个组合数相加,
等于上标取大,下标加1的组合数
(2)可用于合并,简化运算
如
例3 在100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件。
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件次品的抽法有多少种?
(2)(分步)从2件次品中抽出1件有种抽法,从98件合格品中抽出2件的抽法有种,
因此抽出的3件中恰好有1件次品的抽法种数为
解:(1)这是个从100个元素中取3个的组合问题,所以抽法的种数为
例3 在100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件。
(3)抽出的3件中至少有1件次品的抽法有多少种?
(3)方法1(直接法):3件产品中至少1件为次品,包括有1件次品和2件次品两种情况,
根据分类加法计数原理,抽出的3件中至少有1件次品的抽法种数为
方法2(间接法):至少有1件次品的反面是没有次品,即全是合格品。“至少1件次品”就是“任取3件”减去“3件都是合格品”即
“先分类,后分步”
追问:你能总结一下解决组合问题的思路和方法吗?
1.将具体问题抽象为组合问题模型;
2.对于综合问题,一般采取“先分类,后分步”的解题策略
3.研究有关“至多”或“至少”这样的计数问题时,可以直接分类研究,或运用“间接法”计数。
利用信息技术、科学计算器等计算组合数
四、课堂小结
1.组合数公式:
2.组合数性质:
3.解决组合问题:
“先分类,后分步”
直接法、间接法
提高分析问题、解决问题的能力,
发展数学运算、逻辑推理、数学建模等核心素养
五、课后作业
1.计算(1) (2) (3) (4)3-2
2.求证:(1) (2)
3.从含有3件次品的100件产品中,任意抽取5件进行检验。
(1)抽出的产品都是合格品的抽法有多少种?
(2)抽出的产品中恰好有2件是次品的抽法有多少种?
(3)抽出的产品中至少有2件是次品的抽法有多少种?
(4)抽出的产品中至多有2件是次品的抽法有多少种?
再会!
6.2.4 组合数
一、温故知新
问题1 从集合中取出3个元素组成三元子集,共有
哪些不同的子集?
二、新知探究
组合数概念:从个不同元素中取出个元素的所有不同组合的个数,叫做从个不同元素中取出个元素的组合数,记作。
例如,从4个不同元素中取出3个元素的组合数表示为
组合与组合数的区别:
组合数是一个非零自然数
组合不是一个数字
问题2 前面已经提到,组合和排列有关系,我们能否利用这种关系,
由排列数来求组合数呢?
二、新知探究
追问:从4个不同的元素中取出3个元素的排列数与组合数有什么关系?
分析:从这4个元素中取出3个元素的排列数是
从这4个元素中取出3个元素的组合数是
组合
排列
=4
6
=24
6
6
6
=
=
左式 从4个元素中取出3个元素的排列数
右式 第1步:从4个元素中取出3个元素作为一组,共有种取法
第2步:将取出的3个元素作全排列,共有种排法
根据分步乘法计数原理,有,即
=4
一般地,求“从个不同元素中任取个元素的排列数”,可以由以下两步得到:
第1步:从个不同元素中任取个元素作为一组,共有种不同的取法;
第2步:将取出的个元素作全排列,共有种不同的排法。
根据分步乘法计数原理,有,因此
追问(2):由的公式,你能得到的公式吗?
连乘形式
阶乘形式
组合数公式:
规定:
三、学以致用
例1 计算:(1) (2) (3) (4)
解:根据组合数公式,可得
(1)
(2)
(3)
(4)
追问:观察(1)与(2),(3)与(4)的结果,你有什么发现和猜想?
,
特征:两个组合数的下标相同,上标相加等于下标
猜想
证明:
方法1:组合数的意义
方法2:组合数的计算
取出个元素的组合 留下个元素的组合
“一一对应”
所以等式成立
组合数的性质1:
(1)反映了组合数的对称性
(2)当时,可以将计算转化为计算,有助于简化运算
例2:一个口袋里有7个不同的白球和1个红球,从中取出5个球:
(1)共有多少种不同的取法?
(2)如果必须取红球,共有多少种不同的取法?
解:(1)从8个球中取出5个,是一个组合问题,方法数为
。
(2)红球只有1个,问题转化为“从7个白球中取出4个”,也是一个组合问题,
有 种取法。
56
例2 一个口袋里有7个不同的白球和1个红球,从中取出5个球:
(3)如果不取红球,共有多少种不同的取法?
(3)方法1:问题转化为“从7个不同白球中取出5个白球”,
故有种取法。
方法2:“不取红球”的反面是必须取红球,
从“任意取出5个球”中,去掉“必须取红球”即可
有种取法
直接法
间接法
追问:你能解释 的意义吗?
分析:一个口袋里有7个不同的白球和1个红球,从中取出5个球
左式 从8个元素中任取5个,共有种取法
根据分类加法计数原理,
猜想:
右式 第1类:不含特殊元素(红球),共有种取法;
第2类:含有特殊元素(红球),共有种取法
证明:
方法1:从组合数的意义
(从含有1个特殊元素的个元素中任取个的组合)
左式 从(个元素中任取个,共有种取法
右式 第1类:不含特殊元素,共有种取法;
第2类:含有特殊元素,共有种取法
根据分类加法计数原理,
方法2:从组合数的计算(课后作业)
组合数的性质2:
(1)特征:下标相同,上标相差1的两个组合数相加,
等于上标取大,下标加1的组合数
(2)可用于合并,简化运算
如
例3 在100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件。
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件次品的抽法有多少种?
(2)(分步)从2件次品中抽出1件有种抽法,从98件合格品中抽出2件的抽法有种,
因此抽出的3件中恰好有1件次品的抽法种数为
解:(1)这是个从100个元素中取3个的组合问题,所以抽法的种数为
例3 在100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件。
(3)抽出的3件中至少有1件次品的抽法有多少种?
(3)方法1(直接法):3件产品中至少1件为次品,包括有1件次品和2件次品两种情况,
根据分类加法计数原理,抽出的3件中至少有1件次品的抽法种数为
方法2(间接法):至少有1件次品的反面是没有次品,即全是合格品。“至少1件次品”就是“任取3件”减去“3件都是合格品”即
“先分类,后分步”
追问:你能总结一下解决组合问题的思路和方法吗?
1.将具体问题抽象为组合问题模型;
2.对于综合问题,一般采取“先分类,后分步”的解题策略
3.研究有关“至多”或“至少”这样的计数问题时,可以直接分类研究,或运用“间接法”计数。
利用信息技术、科学计算器等计算组合数
四、课堂小结
1.组合数公式:
2.组合数性质:
3.解决组合问题:
“先分类,后分步”
直接法、间接法
提高分析问题、解决问题的能力,
发展数学运算、逻辑推理、数学建模等核心素养
五、课后作业
1.计算(1) (2) (3) (4)3-2
2.求证:(1) (2)
3.从含有3件次品的100件产品中,任意抽取5件进行检验。
(1)抽出的产品都是合格品的抽法有多少种?
(2)抽出的产品中恰好有2件是次品的抽法有多少种?
(3)抽出的产品中至少有2件是次品的抽法有多少种?
(4)抽出的产品中至多有2件是次品的抽法有多少种?
再会!
