7.1.2全概率公式课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(23张PPT)
文档属性
| 名称 | 7.1.2全概率公式课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 707.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 09:29:19 | ||
图片预览




文档简介
(共23张PPT)
第七章 随机变量及其分布
7.1 条件概率与全概率公式
7.1.2 全概率公式
条件概率
1.定义:一般地,设A,B为两个随机事件,且P(A)>0,我们称 P(B|A)
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
2.概率的乘法公式:对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B|A).我们称该式为概率的乘法公式.
热身训练——回顾旧知
2.已知 ( )
A. B. C. D.
热身训练——回顾旧知
C
解:设A=“下雨”,B=“刮风”,AB=“既刮风又下雨”,则
C
条件概率
概率的乘法公式
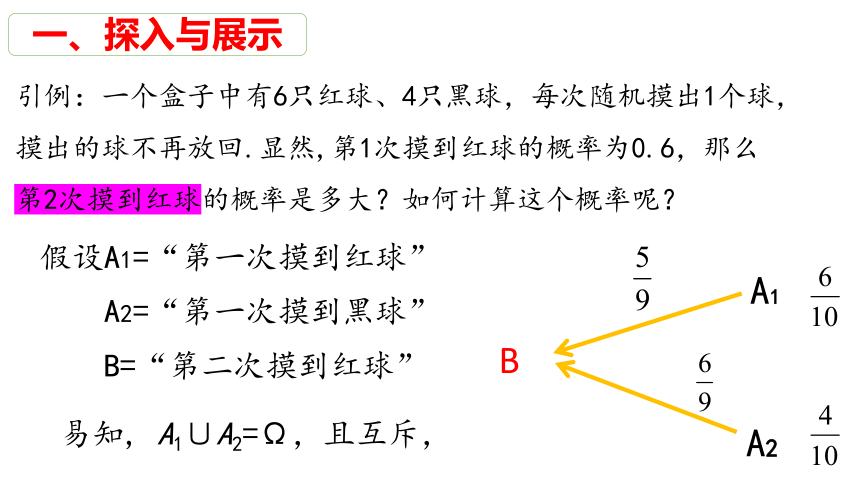
一、探入与展示
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
假设A1=“第一次摸到红球”
A2=“第一次摸到黑球”
B=“第二次摸到红球”
A2
A1
B
易知, A1∪A2=Ω,且互斥,
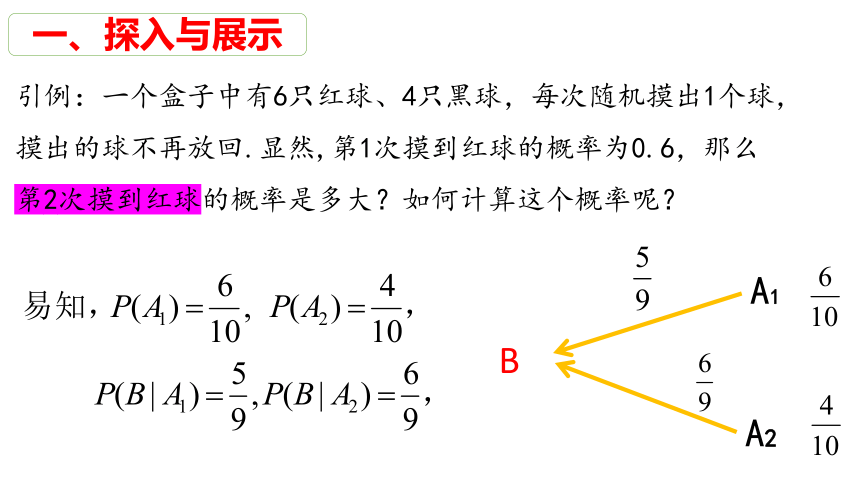
一、探入与展示
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
A2
A1
B
一、探入与展示
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
A2
A1
B
所以,第2次摸到红球的概率是0.6.
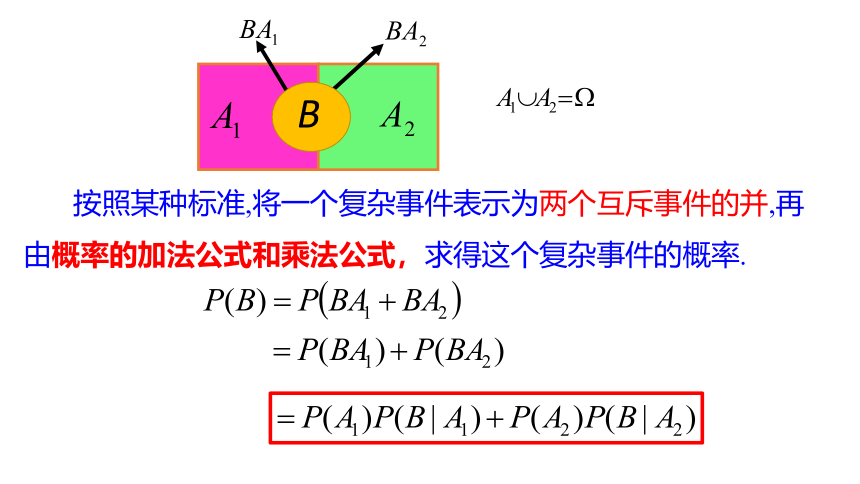
加法公式
乘法公式
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式,求得这个复杂事件的概率.
B
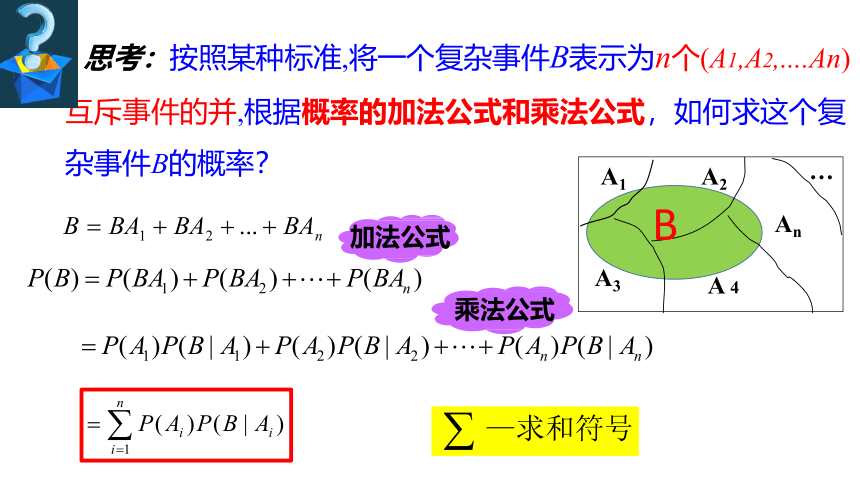
思考:按照某种标准,将一个复杂事件B表示为n个(A1,A2,....An)互斥事件的并,根据概率的加法公式和乘法公式,如何求这个复杂事件B的概率?
A1
A2
A3
An
A 4
…
B
加法公式
乘法公式
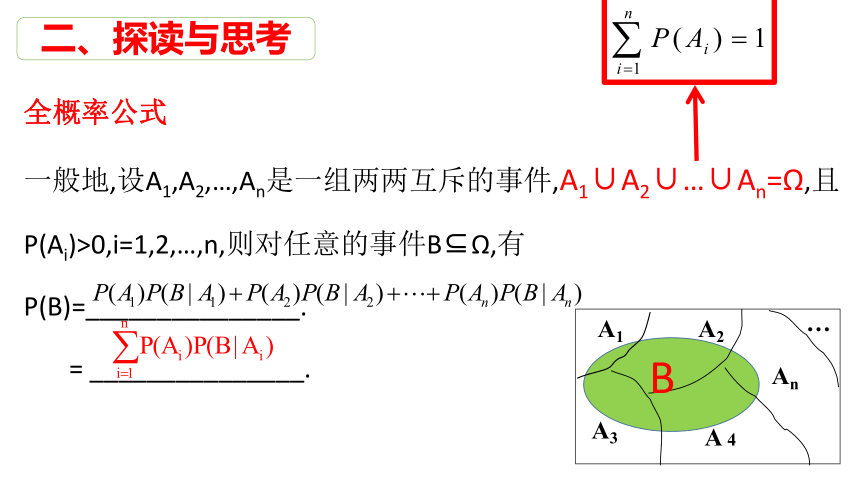
全概率公式
一般地,设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,且P(Ai)>0,i=1,2,…,n,则对任意的事件B Ω,有
P(B)=_______________.
= _______________.
二、探读与思考
A1
A2
A3
An
A 4
…
B
10
二、探读与思考
例1:某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率。
解:设A1=“第1天去A餐厅用餐”,
A2=“第1天去B餐厅用餐”,
B=“第2天去A餐厅用餐”,
B
0.5
0.5
A2
A1
0.6
0.8
设事件
则Ω=
,
根据题意P(A1)=P(A2)=0.5,
P(B|A1)=0.6,
P(B|A2)=0.8,
由因求果
三、探疑与点拨
写概率
例1:某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率。
由全概率公式,得
P(B)= P(A1) P(B| A1)+ P(A2) P(B| A2)
=0.5 0.6+0.5 0.8
=0.7
因此,王同学第2天去A餐厅用餐的概率为0.7.
B
A2
A1
0.5
0.5
0.6
0.8
代公式
由因求果
三、探疑与点拨
【小结】
全概率公式求概率的步骤:
1.设事件:把事件B(结果事件)看作某一过程的结果,把A1,A2,…,An
看作导致结果的若干个原因;
2.写概率:由已知,写出每一原因发生的概率(即P(Ai )),
且每一原因对结果的影响程度(即P(B|Ai ));
3.代公式:用全概率公式计算结果发生的概率(即P(B) ).
由因求果
例2:某人去某地,乘火车、轮船、汽车、飞机的概率分别为0.3,0.2,0.1,0.4,乘坐这四种交通工具迟到的概率分别为 0.25,0.3,0.1,0.2,求他迟到的概率.
解:设A1=“乘火车去”,
A2=“乘轮船去”,
A3=“乘汽车去”,
A4=“乘飞机去”,
B=“迟到”.
易知, A1∪A2∪A3∪A4=Ω,
且两两互斥,
B
A1
A2
A3
A4
0.3
0.2
0.1
0.4
0.25
0.3
0.1
0.2
由因求果
设事件
四、引导与迁移
例2:某人去某地,乘火车、轮船、汽车、飞机的概率分别为0.3,0.2,0.1,0.4,乘坐这四种交通工具迟到的概率分别为 0.25,0.3,0.1,0.2,求他迟到的概率.
由已知得
P(A1)=0.3, P(A2)=0.2,
P(A3) =0.1, P(A4)=0.4,
P(B|A1)=0.25, P(B|A2)=0.3,
P(B|A3) =0.1, P(B|A4)=0.2,
=0.3×0.25+ 0.2×0.3+ 0.1×0.1+ 0.4×0.2=0.225
B
A1
A2
A3
A4
0.3
0.2
0.1
0.4
0.25
0.3
0.1
0.2
由因求果
写概率
代公式
四、引导与迁移
16
变式:例2中,条件不变,问题变为:
“他迟到了,求他乘汽车迟到的概率”.
贝叶斯公式
已知结果
四、引导与迁移
求原因
分析:就是计算在B发生的条件下,事件A3发生的概率.
对分子用乘法公式
分母用
全概率公式
9
*贝叶斯公式
k
P(Ai )P( B | Ai )
i 1
P(A | B) P(Ak )P( B | Ak ) ; k 1, 2,..., n,
证明:
由条件概率的公式:
k
P( B)
P(A | B) P(Ak B)
P(Ak )P(B | Ak ) .
P(Ai )P( B | Ai )
i 1
对分子用乘法公式
对分母用全概 率公式
一般地,设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,且P(Ai)>0,i=1,2,…,n,则对任意的事件B Ω,P(B)>0,有
执果寻因
五、引申与评价
贝叶斯公式
全概率公式
五、引申与评价
全概率公式
五、引申与评价
21
由因求果
执果寻因
课
堂
小
结
1.设事件
2.写概率
3.代公式
加法公式
乘法公式
22
作业:
课本52页:练习1-2题
53页:第5题
再见
第七章 随机变量及其分布
7.1 条件概率与全概率公式
7.1.2 全概率公式
条件概率
1.定义:一般地,设A,B为两个随机事件,且P(A)>0,我们称 P(B|A)
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
2.概率的乘法公式:对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B|A).我们称该式为概率的乘法公式.
热身训练——回顾旧知
2.已知 ( )
A. B. C. D.
热身训练——回顾旧知
C
解:设A=“下雨”,B=“刮风”,AB=“既刮风又下雨”,则
C
条件概率
概率的乘法公式
一、探入与展示
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
假设A1=“第一次摸到红球”
A2=“第一次摸到黑球”
B=“第二次摸到红球”
A2
A1
B
易知, A1∪A2=Ω,且互斥,
一、探入与展示
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
A2
A1
B
一、探入与展示
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
A2
A1
B
所以,第2次摸到红球的概率是0.6.
加法公式
乘法公式
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式,求得这个复杂事件的概率.
B
思考:按照某种标准,将一个复杂事件B表示为n个(A1,A2,....An)互斥事件的并,根据概率的加法公式和乘法公式,如何求这个复杂事件B的概率?
A1
A2
A3
An
A 4
…
B
加法公式
乘法公式
全概率公式
一般地,设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,且P(Ai)>0,i=1,2,…,n,则对任意的事件B Ω,有
P(B)=_______________.
= _______________.
二、探读与思考
A1
A2
A3
An
A 4
…
B
10
二、探读与思考
例1:某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率。
解:设A1=“第1天去A餐厅用餐”,
A2=“第1天去B餐厅用餐”,
B=“第2天去A餐厅用餐”,
B
0.5
0.5
A2
A1
0.6
0.8
设事件
则Ω=
,
根据题意P(A1)=P(A2)=0.5,
P(B|A1)=0.6,
P(B|A2)=0.8,
由因求果
三、探疑与点拨
写概率
例1:某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率。
由全概率公式,得
P(B)= P(A1) P(B| A1)+ P(A2) P(B| A2)
=0.5 0.6+0.5 0.8
=0.7
因此,王同学第2天去A餐厅用餐的概率为0.7.
B
A2
A1
0.5
0.5
0.6
0.8
代公式
由因求果
三、探疑与点拨
【小结】
全概率公式求概率的步骤:
1.设事件:把事件B(结果事件)看作某一过程的结果,把A1,A2,…,An
看作导致结果的若干个原因;
2.写概率:由已知,写出每一原因发生的概率(即P(Ai )),
且每一原因对结果的影响程度(即P(B|Ai ));
3.代公式:用全概率公式计算结果发生的概率(即P(B) ).
由因求果
例2:某人去某地,乘火车、轮船、汽车、飞机的概率分别为0.3,0.2,0.1,0.4,乘坐这四种交通工具迟到的概率分别为 0.25,0.3,0.1,0.2,求他迟到的概率.
解:设A1=“乘火车去”,
A2=“乘轮船去”,
A3=“乘汽车去”,
A4=“乘飞机去”,
B=“迟到”.
易知, A1∪A2∪A3∪A4=Ω,
且两两互斥,
B
A1
A2
A3
A4
0.3
0.2
0.1
0.4
0.25
0.3
0.1
0.2
由因求果
设事件
四、引导与迁移
例2:某人去某地,乘火车、轮船、汽车、飞机的概率分别为0.3,0.2,0.1,0.4,乘坐这四种交通工具迟到的概率分别为 0.25,0.3,0.1,0.2,求他迟到的概率.
由已知得
P(A1)=0.3, P(A2)=0.2,
P(A3) =0.1, P(A4)=0.4,
P(B|A1)=0.25, P(B|A2)=0.3,
P(B|A3) =0.1, P(B|A4)=0.2,
=0.3×0.25+ 0.2×0.3+ 0.1×0.1+ 0.4×0.2=0.225
B
A1
A2
A3
A4
0.3
0.2
0.1
0.4
0.25
0.3
0.1
0.2
由因求果
写概率
代公式
四、引导与迁移
16
变式:例2中,条件不变,问题变为:
“他迟到了,求他乘汽车迟到的概率”.
贝叶斯公式
已知结果
四、引导与迁移
求原因
分析:就是计算在B发生的条件下,事件A3发生的概率.
对分子用乘法公式
分母用
全概率公式
9
*贝叶斯公式
k
P(Ai )P( B | Ai )
i 1
P(A | B) P(Ak )P( B | Ak ) ; k 1, 2,..., n,
证明:
由条件概率的公式:
k
P( B)
P(A | B) P(Ak B)
P(Ak )P(B | Ak ) .
P(Ai )P( B | Ai )
i 1
对分子用乘法公式
对分母用全概 率公式
一般地,设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,且P(Ai)>0,i=1,2,…,n,则对任意的事件B Ω,P(B)>0,有
执果寻因
五、引申与评价
贝叶斯公式
全概率公式
五、引申与评价
全概率公式
五、引申与评价
21
由因求果
执果寻因
课
堂
小
结
1.设事件
2.写概率
3.代公式
加法公式
乘法公式
22
作业:
课本52页:练习1-2题
53页:第5题
再见
