2021-2022学年鲁教版(五四制)八年级数学下册第6章特殊平行四边形单元达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册第6章特殊平行四边形单元达标测试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 503.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 21:46:00 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学下册《第6章特殊平行四边形》单元达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.如图,P点为矩形ABCD两对角线的交点,将P点分别以AD、BC为对称轴画出对称点Q、R,形成六边形QABRCD.若AB=2,AD=4,则六边形QABRCD的周长为何?( )
A.12 B.4+2 C.4+4 D.4+4
2.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=4,则正方形的面积为( )
A.5 B.6 C.7 D.8
3.如图,在矩形ABCD中,AB=1,AD=,O是对角线的交点,过C作CE⊥BD于点E,EC的延长线与∠BAD的平分线相交于点H,AH与BC交于点F.给出下列四个结论:①AF=FH;②BF=BO;③AC=CH;④BE=3DE.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
4.如图,P为菱形ABCD内一动点,连接PA,PB,PD,∠APD=∠BAD=60°,AB=2,则PB+PD的最大值为( )
A. B. C. D.
5.如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离是;③EB⊥ED;④S正方形ABCD=4+.其中正确的结论是( )
A.①② B.①④ C.①③④ D.①②③
6.如图,在边长为2的正方形EFGH中,M,N分别为EF与GH的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当y=时,x的值为( )
A.或2+ B.或2﹣ C.2± D.或
7.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
8.如图,若正方形ABCD的边长为14,正方形IJKL的边长为2,则正方形EFGH的边长为( )
A.6 B.8 C.10 D.12
9.如图,等边△ABC与正方形DEFG重叠,其中D、E两点分别在AB、BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )
A.1 B.2 C. D.4
10.如图,正方形ABCD和正方形CGEF的边长分别是2和3,且点B,C,G在同一直线上,M是线段AE的中点,连接MF,则MF的长为( )
A. B. C.2 D.
二.填空题(共8小题,满分24分)
11.如图所示,在矩形ABCD中,DE平分∠ADC,且∠EDO等于15°,∠DOE= °.
12.如图,在矩形ABCD中,EF为对角线BD的垂直平分线,分别交AD、BC于点E、F,连接AO,若AO=,AB=4,则EF= .
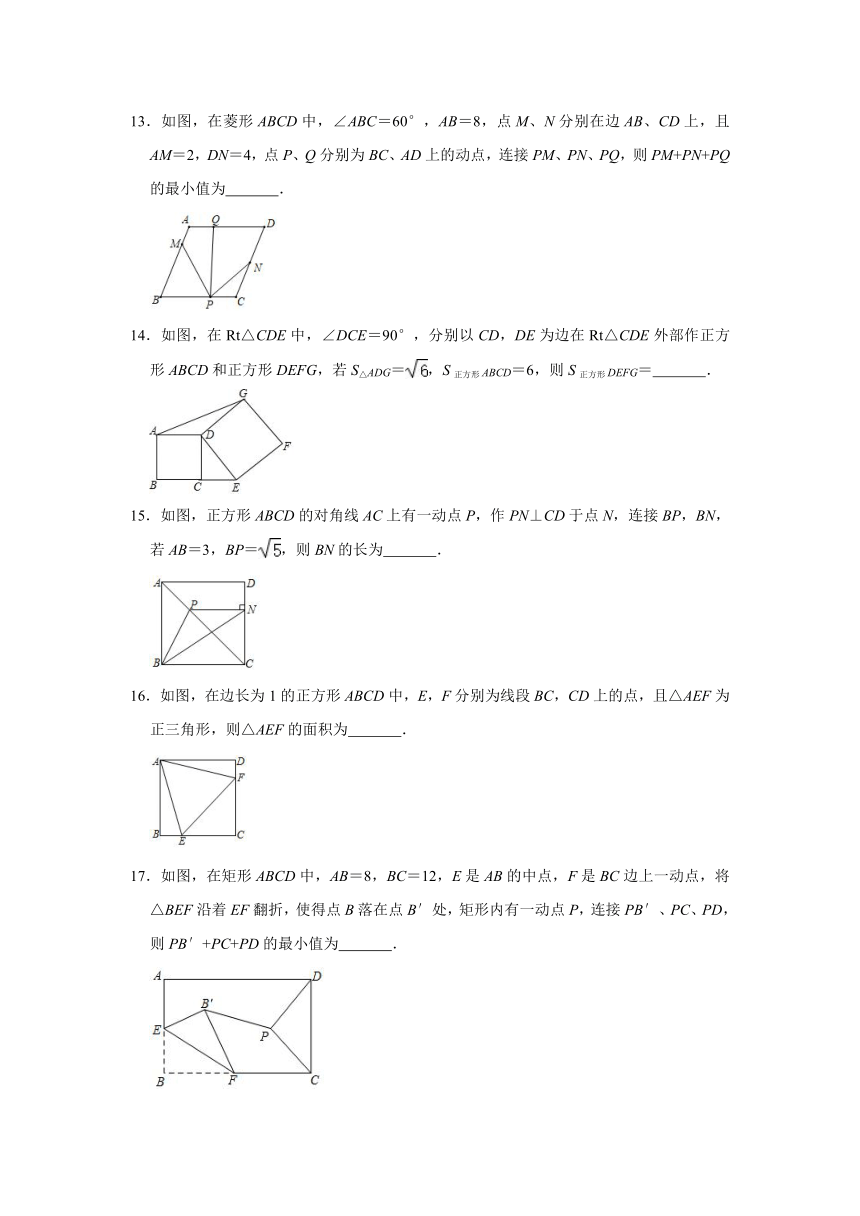
13.如图,在菱形ABCD中,∠ABC=60°,AB=8,点M、N分别在边AB、CD上,且AM=2,DN=4,点P、Q分别为BC、AD上的动点,连接PM、PN、PQ,则PM+PN+PQ的最小值为 .
14.如图,在Rt△CDE中,∠DCE=90°,分别以CD,DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,若S△ADG=,S正方形ABCD=6,则S正方形DEFG= .
15.如图,正方形ABCD的对角线AC上有一动点P,作PN⊥CD于点N,连接BP,BN,若AB=3,BP=,则BN的长为 .
16.如图,在边长为1的正方形ABCD中,E,F分别为线段BC,CD上的点,且△AEF为正三角形,则△AEF的面积为 .
17.如图,在矩形ABCD中,AB=8,BC=12,E是AB的中点,F是BC边上一动点,将△BEF沿着EF翻折,使得点B落在点B′处,矩形内有一动点P,连接PB′、PC、PD,则PB′+PC+PD的最小值为 .
18.如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;④∠AMN﹣∠AMB=60°.其中正确结论的序号是 .
三.解答题(共8小题,满分66分)
19.在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF、BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF平分∠DAB.
20.如图, ABCD的对角线AC、BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度向点O运动,点F在线段OD上从点O以2cm/s的速度向点D运动.
(1)若点E、F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形.
(2)在(1)的条件下,当AB为何值时, AECF是菱形;
(3)求(2)中菱形AECF的面积.
21.如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
(1)求证:四边形PBQD是平行四边形
(2)若AD=6cm,AB=4cm,点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为ts,请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形.并求出此时菱形的周长.
22.如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
23.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
24.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图2若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
25.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由.
26.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
(1)如图1,当∠MAN绕点A旋转到BM=DN时,有BM+DN=MN.当∠MAN绕点A旋转到BM≠DN时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间有怎样的等量关系?请写出你的猜想,并证明.
参考答案
一.选择题(共10小题,满分30分)
1.解:如图,连接PQ交AD于点E,
根据题意可知:
QP和AD互相垂直平分,
∴AE=DE=2,PE=QE=1,AQ=DQ,
∴AQ==,
∴AQ=DQ=,
同理可得,BR=CR=,
则六边形QABRCD的周长为4AQ+2AB=4+4.
故选:D.
2.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
方法一:∴a+b=4,
∵CE DE=4,
CD2=a2+b2=(a+b)2﹣2ab=42﹣2×4=8,
∴S正方形ABCD=8.
方法二:方程组a+b=4,ab=4的解为:a=b=2.
此时DE、CB的长就是正方形OMEN的边长,
即正方形OMEN就是正方形OCED.
所以DC=OE=2,
所以面积为8.故选:D.
3.解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AF是∠BAD的平分线,
∴∠FAB=45°,
∴∠AFB=45°,
∴∠AFC=135°,CF与AH不垂直,
∴点F不是AH的中点,即AF≠FH,
∴①错误;
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=,AB=1,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,∴②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO﹣∠CAH=30°﹣15°=15°=∠CAH,
∴AC=CH,
∴③正确;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,
∵CE⊥BD,
∴DE=EO=DO=BD,
即BE=3ED,∴④正确;
所以其中正确结论有②③④,3个.故选:C.
4.解:如图,连接BD.在菱形ABCD中,
AB=AD.
∵∠BAD=60°.
∴△ABD是等边三角形,
∴DA=DB,∠ABD=60°.
∵∠APD=∠BAD=60°.
∴动点P一定在△ABD的外接圆⊙O的劣弧BD上,
∴∠BPD=∠APD+∠APB=∠APD+∠ADB=120°.
在AP上取AE=BP,连接DE.
∵AE=BP,∠DAE=∠DBP,DA=DB,
∴△AED≌△BPD(SAS),
∴DE=DP,∠AED=∠BPD=120°,
∴∠DEP=60°,
∴△PDE为等边三角形,
∴PE=PD,
∴AP=AE+EP=BP+PD.
当AP为⊙O的直径时,BP+PD的值最大,
此时∠ABP=90°,∠PAB=30°.
∵AB=2,
∴PB+PD的最大值为.故选:B.
5.解:∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,,
∴△APD≌△AEB(SAS);故①正确;
由△APD≌△AEB得,∠AEP=∠APE=45°,从而∠APD=∠AEB=135°,
所以∠BEP=90°,
过B作BF⊥AE,交AE的延长线于F,则BF的长是点B到直线AE的距离,
在△AEP中,由勾股定理得PE=,
在△BEP中,PB=,PE=,由勾股定理得:BE=,
∵∠PAE=∠PEB=∠EFB=90°,AE=AP,
∴∠AEP=45°,
∴∠BEF=180°﹣45°﹣90°=45°,
∴∠EBF=45°,
∴EF=BF,
在△EFB中,由勾股定理得:EF=BF=,
故②是错误的;
因为△APD≌△AEB,所以∠ADP=∠ABE,而对顶角相等,所以③是正确的;
连接BD,则S△BPD=PD×BE=,
所以S△ABD=S△APD+S△APB+S△BPD=2+,
所以S正方形ABCD=2S△ABD=4+所以④是正确的;
综上可知,正确的有①③④,
故选:C.
6.解:如图1中,当过A在正方形内部时,连接EG交MN于O,连接OF,设AB交EH于Q,AC交FG于P.
由题意,△ABC是等腰直角三角形,AQ=OE=OG=AP=OF,S△OEF=1,
∵y=,
∴S四边形AOEQ+S四边形AOFP=1.5,
∴OA 2=1.5,
∴OA=,
∴AM=1+=.
如图2中,当点A在正方形外部时,
由题意,重叠部分是六边形WQRJPT,S重叠=S△ABC﹣2S△BQR﹣S△AWT,
∴2.5=××﹣1﹣×2AN×AN,
解得AN=,
∴AM=2+,
综上所述,满足条件的AM的值为或2+,
故选:A.
7.解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
故选:B.
8.解:由图可得,S△AEH+S△BFE+S△CGF+S△DHG=S△HJE+S△EKF+S△FLG+S△GIH,
设S△AEH+S△BFE+S△CGF+S△DHG=S△HJE+S△EKF+S△FLG+S△GIH=x,
则S正方形EFGH=S正方形ABCD﹣x=S正方形IJKL+x,
即196﹣x=4+x,
解得x=96,
∴S正方形EFGH=196﹣96=100,
∴正方形EFGH的边长为10,
故选:C.
9.解:过F作FQ⊥BC于Q,则∠FQE=90°,
∵△ABC是等边三角形,AB=6,
∴BC=AB=6,∠B=60°,
∵BD=BE,DE=2,
∴△BED是等边三角形,且边长为2,
∴BE=DE=2,∠BED=60°,
∴CE=BC﹣BE=4,
∵四边形DEFG是正方形,DE=2,
∴EF=DE=2,∠DEF=90°,
∴∠FEC=180°﹣60°﹣90°=30°,
∴QF=EF=1,
∴△EFC的面积为==2,
故选:B.
10.解:延长AD至H,延长FM与AH交于H点,
则在△AMH和△EMF中,
,
∴△AMH≌△EMF,即FM=MH,AH=EF,
∴DH=AH﹣AD=EF﹣AD=1,
∵DF=CF﹣CD=3﹣2=1,
在直角△DFH中,FH为斜边,
解直角△DFH得:FH=,
又∵FM=MH,
∴FM=,
故选:B.
二.填空题(共8小题,满分24分)
11.解:∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AO=CO,BO=DO,AC=BD,
∴OA=OD,
∵DE平分∠ADC
∴∠CDE=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AD=AE,
又∵∠EDO=15°,
∴∠ADO=60°;
∴△OAD是等边三角形,
∴∠AOD=∠OAD=60°,
∴AD=AO=DO,
∴AO=AE,
∴∠AOE=∠AEO,
∵∠OAE=90°﹣∠OAD=30°,
∴∠AOE=∠AEO=(180°﹣30°)=75°,
∴∠DOE=60°+75°=135°,
故答案为:135.
12.解:连接DF,
∵EF为矩形ABCD的对角线BD的垂直平分线,AO=,
∴BD=2DO=2AO=,BF=DF,∠DOF=90°,
∴DO=,
在矩形ABCD中,∠C=90°,CD=AB=4,AD∥BC,
∴BD2=BC2+CD2,
即,
解得BC=6,
∵DF2=CF2+CD2,
∴DF2=(6﹣DF)2+42,
解得DF=,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=∠DOF=90°,
∵AD∥BC,
∴∠EDO=∠FBO,
∴△EDO≌△FBO(ASA),
∴OE=OF=EF,
在Rt△DOF中,DF2=OF2+OD2,
∴OF2+()2=()2,
解得OF=,
∴EF=.
故答案为.
13.解:如图所示,过点M作MF⊥OC于F,过点A作AH⊥OC于H,作点N关于x轴的对称点N′,连接MN′交OC于P,连接NN′交OC于E,此时PM+PN的值最小.
∵四边形ABCD是菱形,
∴AB=BC=AD=CD=8,AO∥CD,
∴∠OOC=∠NCE=60°,
∵AH⊥OC,
∴AH=4,
∵AM=2,
∴OM=6,
∵MF⊥OC,
∴∠MFO=90°,∠FMO=30°,
∴OF=OM=3,MF=OF=3,
∴M(3,3),
∵DN=CN=4,NE⊥x轴,
∴∠NEC=90°,∠CNE=30°,
∴CE=CN=2,NE=CE=2,
∴N(10,2),N′(10,﹣2),
∴PM+PN=PM+PN′=MN′==2,
根据垂线段最短,当PQ⊥AD时,PQ的值最小,最小值=AH=4,
∴PM+PM+PQ是最小值为2+4.
故答案为2+4.
14.解:如图所示,过G作GH⊥AD,交AD的延长线于H,则∠H=90°,
又∵∠DCE=90°,
∴∠H=∠DCE,
∵四边形ABCD和四边形DEFG是正方形,
∴∠ADC=∠CDH=∠EDG=90°,DG=DE,
∴∠GDH=∠EDC,
∴△DGH≌△DEC(AAS),
∴GH=CE,
∵S正方形ABCD=6,
∴CD=,
∵S△ADG=,
∴AD×GH=,
又∵AD=CD,
∴CD×CE=,即×CE=,
∴CE=2,
∴Rt△CDE中,DE===,
∴S正方形DEFG=DE2=10,故答案为:10.
15.解:延长NP交AB于H,
∵四边形ABCD为正方形,
∴∠BCD=90°,AB∥CD,∠BAC=45°,
∵PN⊥CD,
∴PN⊥AB,
∴∠HAP=∠HPA=45°,
∴AH=PH,
设AH=PH=x,则BH=3﹣x,
在Rt△PBH中,PB2=PH2+BH2,
∴,
解得x=1或2,
当x=1时,BH=CN=2,在Rt△BCN中,;
当x=2时,BH=CN=1,在Rt△BCN中,.
故答案为或.
16.解:∵四边形ABCD是正方形,
∴∠B=∠D=90°,AB=AD,
∵△AEF是等边三角形,
∴AE=EF=AF,
在Rt△ABE和Rt△ADF中,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,
设BE=x,那么DF=x,CE=CF=1﹣x,
在Rt△ABE中,AE2=AB2+BE2,
在Rt△CEF中,FE2=CF2+CE2,
∴AB2+BE2=CF2+CE2,
∴x2+1=2(1﹣x)2,
∴x2﹣4x+1=0,
∴x=2±,而x<1,
∴x=2﹣,
即BE的长为=2﹣,
∴CE=CF=﹣1.
∴△AEF的面积=1×1﹣2××1×(2﹣)﹣(﹣1)2=2﹣3,
故答案为:2﹣3.
17.解:将△PDC绕点D逆时针旋转60°,得到△DP′C′,连接PP′,CP′,EC'.
由题意,AE=EB=EB′,
∴点B′在上运动,
由作图可知,△PDP′,△DCC′都是等边三角形,
∴DP=PP′,
∵CP=P′C′,
∴PB′+PD+PC=PB′+PP′+P′C′,
∵EB′+PB′+PP′+P′C′≥EC',
∴PB′+PP′+P′C′≥12+4﹣4,
∴PB′+PP′+P′C′≥8+4,
∴PB′+PC+PD的最小值为8+4,
故答案为:8+4.
18.解:①:∵正方形ABCD中,AB=AD,∠B=∠ADC=∠C=90°
∴MN2=MC2+NC2
当MN=MC时,
MN2=2MC2,
∴MC2=NC2,
∴MC=NC,
∴BM=DN,
∴△ABM≌△ADN(SAS)
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM=22.5°,故①正确;
②:如图,将△ABM绕点A顺时针旋转90°得△ADE,
则∠EAN=∠EAM﹣∠MAN=90°﹣45°=45°,
则在△EAN和△MAN中,
,
∴△EAN≌△MAN(SAS)
∴∠AMN=∠AED,
∴∠AED+∠EAM+∠ENM+∠AMN=360°,
∴2∠AMN+90°+(180°﹣∠MNC)=360°,
∴2∠AMN﹣∠MNC=90°,
故②正确;
③:∵△EAN≌△MAN,
∴MN=EN=DE+DN=BM+DN,
∴△MNC的周长为:
MC+NC+MN=(MC+BM)+(NC+DN)=DC+BC,
∵DC和BC均为正方形ABCD的边长,故△MNC的周长不变.故③正确;
④如图,将△ADN绕点A逆时针旋转90°得△ABF,
∴∠MAF=90°﹣∠MAN=45°,
∴∠MAN=∠MAF,
在△MAN和△MAF中,
,
∴△MAN≌△MAF(SAS),
∴∠AMN=∠AMB,
故④错误.
综上①②③正确.
故答案为:①②③.
三.解答题(共8小题,满分66分)
19.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC==10,
∴AD=BC=DF=10,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
20.解:(1)若四边形AECF为平行四边形,
∴AO=OC,EO=OF,
∵四边形ABCD为平行四边形,
∴BO=OD=6cm,
∴EO=6﹣t,OF=2t,
∴6﹣t=2t,
∴t=2s,
∴当t为2秒时,四边形AECF是平行四边形;
(2)若四边形AECF是菱形,
∴AC⊥BD,
∴AO2+BO2=AB2,
∴AB==3;
∴当AB为3时, AECF是菱形;
(3)∵四边形AECF是菱形,
∴BO⊥AC,OE=OF,
∵四边形ABCD是平行四边形,
∴BO=OD,
∴BE=DF,
∴t=6﹣2t,
∴t=2,
∴BE=DF=2,
∴EF=8,
∴菱形AECF的面积=AC EF=6×8=24.
21.解:(1)∵证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD中点,
∴OB=OD,
在△PDO和△QBO中,
,
∴△PDO≌△QBO(ASA),
∴OP=OQ.
又∵OB=OD,
∴四边形PBQD是平行四边形;
(2)依题意得,AP=tcm,则PD=(6﹣t) cm.
当四边形PBQD是菱形时,有PB=PD=(6﹣t) cm.
∵四边形ABCD是矩形,
∴∠A=90°.
在Rt△ABP中,AP2+AB2=BP2,AB=4cm,
∴t2+42=(6﹣t)2
解得,
所以运动的时间为时,四边形PBQD是菱形.
∴此时菱形的周长为(cm).
22.(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPE=∠EDF=90°;
(3)解:AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
23.解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
24.证明:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
25.(1)证明:∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠DAB=∠GAE=90°,
∴∠GAD=∠EAB,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
26.解:(1)图1中的结论仍然成立,即BM+DN=MN,理由为:
如图2,在MB的延长线上截取BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠DAB=∠ABC=∠ABE=90°,
∵在△ABE和△ADN中
,
∴△ABE≌△ADN(SAS).
∴AE=AN;∠EAB=∠NAD,
∵∠DAB=90°,∠MAN=45°,
∴∠DAN+∠BAM=45°,
∴∠EAM=∠BAM+∠EAB=45°=∠MAN,
∵在△AEM和△ANM中
,
∴△AEM≌△ANM(SAS),
∴ME=MN,
∴MN=ME=BE+BM=DN+BM,
即DN+BM=MN;
(2)猜想:线段BM,DN和MN之间的等量关系为:DN﹣BM=MN.
证明:如图3,在DN上截取DE=MB,连接AE,
∵由(1)知:AD=AB,∠D=∠ABM=90°,BM=DE,
∴△ABM≌△ADE(SAS).
∴AM=AE;∠MAB=∠EAD,
∵∠MAN=45°=∠MAB+∠BAN,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°﹣45°=45°=∠MAN,
∵在△AMN和△AEN中
,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵DN﹣DE=EN,
∴DN﹣BM=MN.
一.选择题(共10小题,满分30分)
1.如图,P点为矩形ABCD两对角线的交点,将P点分别以AD、BC为对称轴画出对称点Q、R,形成六边形QABRCD.若AB=2,AD=4,则六边形QABRCD的周长为何?( )
A.12 B.4+2 C.4+4 D.4+4
2.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=4,则正方形的面积为( )
A.5 B.6 C.7 D.8
3.如图,在矩形ABCD中,AB=1,AD=,O是对角线的交点,过C作CE⊥BD于点E,EC的延长线与∠BAD的平分线相交于点H,AH与BC交于点F.给出下列四个结论:①AF=FH;②BF=BO;③AC=CH;④BE=3DE.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
4.如图,P为菱形ABCD内一动点,连接PA,PB,PD,∠APD=∠BAD=60°,AB=2,则PB+PD的最大值为( )
A. B. C. D.
5.如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离是;③EB⊥ED;④S正方形ABCD=4+.其中正确的结论是( )
A.①② B.①④ C.①③④ D.①②③
6.如图,在边长为2的正方形EFGH中,M,N分别为EF与GH的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当y=时,x的值为( )
A.或2+ B.或2﹣ C.2± D.或
7.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
8.如图,若正方形ABCD的边长为14,正方形IJKL的边长为2,则正方形EFGH的边长为( )
A.6 B.8 C.10 D.12
9.如图,等边△ABC与正方形DEFG重叠,其中D、E两点分别在AB、BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )
A.1 B.2 C. D.4
10.如图,正方形ABCD和正方形CGEF的边长分别是2和3,且点B,C,G在同一直线上,M是线段AE的中点,连接MF,则MF的长为( )
A. B. C.2 D.
二.填空题(共8小题,满分24分)
11.如图所示,在矩形ABCD中,DE平分∠ADC,且∠EDO等于15°,∠DOE= °.
12.如图,在矩形ABCD中,EF为对角线BD的垂直平分线,分别交AD、BC于点E、F,连接AO,若AO=,AB=4,则EF= .
13.如图,在菱形ABCD中,∠ABC=60°,AB=8,点M、N分别在边AB、CD上,且AM=2,DN=4,点P、Q分别为BC、AD上的动点,连接PM、PN、PQ,则PM+PN+PQ的最小值为 .
14.如图,在Rt△CDE中,∠DCE=90°,分别以CD,DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,若S△ADG=,S正方形ABCD=6,则S正方形DEFG= .
15.如图,正方形ABCD的对角线AC上有一动点P,作PN⊥CD于点N,连接BP,BN,若AB=3,BP=,则BN的长为 .
16.如图,在边长为1的正方形ABCD中,E,F分别为线段BC,CD上的点,且△AEF为正三角形,则△AEF的面积为 .
17.如图,在矩形ABCD中,AB=8,BC=12,E是AB的中点,F是BC边上一动点,将△BEF沿着EF翻折,使得点B落在点B′处,矩形内有一动点P,连接PB′、PC、PD,则PB′+PC+PD的最小值为 .
18.如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;④∠AMN﹣∠AMB=60°.其中正确结论的序号是 .
三.解答题(共8小题,满分66分)
19.在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF、BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF平分∠DAB.
20.如图, ABCD的对角线AC、BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度向点O运动,点F在线段OD上从点O以2cm/s的速度向点D运动.
(1)若点E、F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形.
(2)在(1)的条件下,当AB为何值时, AECF是菱形;
(3)求(2)中菱形AECF的面积.
21.如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
(1)求证:四边形PBQD是平行四边形
(2)若AD=6cm,AB=4cm,点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为ts,请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形.并求出此时菱形的周长.
22.如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
23.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
24.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图2若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
25.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由.
26.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
(1)如图1,当∠MAN绕点A旋转到BM=DN时,有BM+DN=MN.当∠MAN绕点A旋转到BM≠DN时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间有怎样的等量关系?请写出你的猜想,并证明.
参考答案
一.选择题(共10小题,满分30分)
1.解:如图,连接PQ交AD于点E,
根据题意可知:
QP和AD互相垂直平分,
∴AE=DE=2,PE=QE=1,AQ=DQ,
∴AQ==,
∴AQ=DQ=,
同理可得,BR=CR=,
则六边形QABRCD的周长为4AQ+2AB=4+4.
故选:D.
2.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
,
∴△COM≌△DON(AAS),
∴OM=ON,CM=DN,
∴四边形OMEN是正方形,
∵OE=2,
∴2NE2=OE2=(2)2=8,
∴NE=ON=2,
∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,
设DE=a,CE=b,
方法一:∴a+b=4,
∵CE DE=4,
CD2=a2+b2=(a+b)2﹣2ab=42﹣2×4=8,
∴S正方形ABCD=8.
方法二:方程组a+b=4,ab=4的解为:a=b=2.
此时DE、CB的长就是正方形OMEN的边长,
即正方形OMEN就是正方形OCED.
所以DC=OE=2,
所以面积为8.故选:D.
3.解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AF是∠BAD的平分线,
∴∠FAB=45°,
∴∠AFB=45°,
∴∠AFC=135°,CF与AH不垂直,
∴点F不是AH的中点,即AF≠FH,
∴①错误;
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=,AB=1,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,∴②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO﹣∠CAH=30°﹣15°=15°=∠CAH,
∴AC=CH,
∴③正确;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,
∵CE⊥BD,
∴DE=EO=DO=BD,
即BE=3ED,∴④正确;
所以其中正确结论有②③④,3个.故选:C.
4.解:如图,连接BD.在菱形ABCD中,
AB=AD.
∵∠BAD=60°.
∴△ABD是等边三角形,
∴DA=DB,∠ABD=60°.
∵∠APD=∠BAD=60°.
∴动点P一定在△ABD的外接圆⊙O的劣弧BD上,
∴∠BPD=∠APD+∠APB=∠APD+∠ADB=120°.
在AP上取AE=BP,连接DE.
∵AE=BP,∠DAE=∠DBP,DA=DB,
∴△AED≌△BPD(SAS),
∴DE=DP,∠AED=∠BPD=120°,
∴∠DEP=60°,
∴△PDE为等边三角形,
∴PE=PD,
∴AP=AE+EP=BP+PD.
当AP为⊙O的直径时,BP+PD的值最大,
此时∠ABP=90°,∠PAB=30°.
∵AB=2,
∴PB+PD的最大值为.故选:B.
5.解:∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,,
∴△APD≌△AEB(SAS);故①正确;
由△APD≌△AEB得,∠AEP=∠APE=45°,从而∠APD=∠AEB=135°,
所以∠BEP=90°,
过B作BF⊥AE,交AE的延长线于F,则BF的长是点B到直线AE的距离,
在△AEP中,由勾股定理得PE=,
在△BEP中,PB=,PE=,由勾股定理得:BE=,
∵∠PAE=∠PEB=∠EFB=90°,AE=AP,
∴∠AEP=45°,
∴∠BEF=180°﹣45°﹣90°=45°,
∴∠EBF=45°,
∴EF=BF,
在△EFB中,由勾股定理得:EF=BF=,
故②是错误的;
因为△APD≌△AEB,所以∠ADP=∠ABE,而对顶角相等,所以③是正确的;
连接BD,则S△BPD=PD×BE=,
所以S△ABD=S△APD+S△APB+S△BPD=2+,
所以S正方形ABCD=2S△ABD=4+所以④是正确的;
综上可知,正确的有①③④,
故选:C.
6.解:如图1中,当过A在正方形内部时,连接EG交MN于O,连接OF,设AB交EH于Q,AC交FG于P.
由题意,△ABC是等腰直角三角形,AQ=OE=OG=AP=OF,S△OEF=1,
∵y=,
∴S四边形AOEQ+S四边形AOFP=1.5,
∴OA 2=1.5,
∴OA=,
∴AM=1+=.
如图2中,当点A在正方形外部时,
由题意,重叠部分是六边形WQRJPT,S重叠=S△ABC﹣2S△BQR﹣S△AWT,
∴2.5=××﹣1﹣×2AN×AN,
解得AN=,
∴AM=2+,
综上所述,满足条件的AM的值为或2+,
故选:A.
7.解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
故选:B.
8.解:由图可得,S△AEH+S△BFE+S△CGF+S△DHG=S△HJE+S△EKF+S△FLG+S△GIH,
设S△AEH+S△BFE+S△CGF+S△DHG=S△HJE+S△EKF+S△FLG+S△GIH=x,
则S正方形EFGH=S正方形ABCD﹣x=S正方形IJKL+x,
即196﹣x=4+x,
解得x=96,
∴S正方形EFGH=196﹣96=100,
∴正方形EFGH的边长为10,
故选:C.
9.解:过F作FQ⊥BC于Q,则∠FQE=90°,
∵△ABC是等边三角形,AB=6,
∴BC=AB=6,∠B=60°,
∵BD=BE,DE=2,
∴△BED是等边三角形,且边长为2,
∴BE=DE=2,∠BED=60°,
∴CE=BC﹣BE=4,
∵四边形DEFG是正方形,DE=2,
∴EF=DE=2,∠DEF=90°,
∴∠FEC=180°﹣60°﹣90°=30°,
∴QF=EF=1,
∴△EFC的面积为==2,
故选:B.
10.解:延长AD至H,延长FM与AH交于H点,
则在△AMH和△EMF中,
,
∴△AMH≌△EMF,即FM=MH,AH=EF,
∴DH=AH﹣AD=EF﹣AD=1,
∵DF=CF﹣CD=3﹣2=1,
在直角△DFH中,FH为斜边,
解直角△DFH得:FH=,
又∵FM=MH,
∴FM=,
故选:B.
二.填空题(共8小题,满分24分)
11.解:∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AO=CO,BO=DO,AC=BD,
∴OA=OD,
∵DE平分∠ADC
∴∠CDE=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AD=AE,
又∵∠EDO=15°,
∴∠ADO=60°;
∴△OAD是等边三角形,
∴∠AOD=∠OAD=60°,
∴AD=AO=DO,
∴AO=AE,
∴∠AOE=∠AEO,
∵∠OAE=90°﹣∠OAD=30°,
∴∠AOE=∠AEO=(180°﹣30°)=75°,
∴∠DOE=60°+75°=135°,
故答案为:135.
12.解:连接DF,
∵EF为矩形ABCD的对角线BD的垂直平分线,AO=,
∴BD=2DO=2AO=,BF=DF,∠DOF=90°,
∴DO=,
在矩形ABCD中,∠C=90°,CD=AB=4,AD∥BC,
∴BD2=BC2+CD2,
即,
解得BC=6,
∵DF2=CF2+CD2,
∴DF2=(6﹣DF)2+42,
解得DF=,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=∠DOF=90°,
∵AD∥BC,
∴∠EDO=∠FBO,
∴△EDO≌△FBO(ASA),
∴OE=OF=EF,
在Rt△DOF中,DF2=OF2+OD2,
∴OF2+()2=()2,
解得OF=,
∴EF=.
故答案为.
13.解:如图所示,过点M作MF⊥OC于F,过点A作AH⊥OC于H,作点N关于x轴的对称点N′,连接MN′交OC于P,连接NN′交OC于E,此时PM+PN的值最小.
∵四边形ABCD是菱形,
∴AB=BC=AD=CD=8,AO∥CD,
∴∠OOC=∠NCE=60°,
∵AH⊥OC,
∴AH=4,
∵AM=2,
∴OM=6,
∵MF⊥OC,
∴∠MFO=90°,∠FMO=30°,
∴OF=OM=3,MF=OF=3,
∴M(3,3),
∵DN=CN=4,NE⊥x轴,
∴∠NEC=90°,∠CNE=30°,
∴CE=CN=2,NE=CE=2,
∴N(10,2),N′(10,﹣2),
∴PM+PN=PM+PN′=MN′==2,
根据垂线段最短,当PQ⊥AD时,PQ的值最小,最小值=AH=4,
∴PM+PM+PQ是最小值为2+4.
故答案为2+4.
14.解:如图所示,过G作GH⊥AD,交AD的延长线于H,则∠H=90°,
又∵∠DCE=90°,
∴∠H=∠DCE,
∵四边形ABCD和四边形DEFG是正方形,
∴∠ADC=∠CDH=∠EDG=90°,DG=DE,
∴∠GDH=∠EDC,
∴△DGH≌△DEC(AAS),
∴GH=CE,
∵S正方形ABCD=6,
∴CD=,
∵S△ADG=,
∴AD×GH=,
又∵AD=CD,
∴CD×CE=,即×CE=,
∴CE=2,
∴Rt△CDE中,DE===,
∴S正方形DEFG=DE2=10,故答案为:10.
15.解:延长NP交AB于H,
∵四边形ABCD为正方形,
∴∠BCD=90°,AB∥CD,∠BAC=45°,
∵PN⊥CD,
∴PN⊥AB,
∴∠HAP=∠HPA=45°,
∴AH=PH,
设AH=PH=x,则BH=3﹣x,
在Rt△PBH中,PB2=PH2+BH2,
∴,
解得x=1或2,
当x=1时,BH=CN=2,在Rt△BCN中,;
当x=2时,BH=CN=1,在Rt△BCN中,.
故答案为或.
16.解:∵四边形ABCD是正方形,
∴∠B=∠D=90°,AB=AD,
∵△AEF是等边三角形,
∴AE=EF=AF,
在Rt△ABE和Rt△ADF中,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,
设BE=x,那么DF=x,CE=CF=1﹣x,
在Rt△ABE中,AE2=AB2+BE2,
在Rt△CEF中,FE2=CF2+CE2,
∴AB2+BE2=CF2+CE2,
∴x2+1=2(1﹣x)2,
∴x2﹣4x+1=0,
∴x=2±,而x<1,
∴x=2﹣,
即BE的长为=2﹣,
∴CE=CF=﹣1.
∴△AEF的面积=1×1﹣2××1×(2﹣)﹣(﹣1)2=2﹣3,
故答案为:2﹣3.
17.解:将△PDC绕点D逆时针旋转60°,得到△DP′C′,连接PP′,CP′,EC'.
由题意,AE=EB=EB′,
∴点B′在上运动,
由作图可知,△PDP′,△DCC′都是等边三角形,
∴DP=PP′,
∵CP=P′C′,
∴PB′+PD+PC=PB′+PP′+P′C′,
∵EB′+PB′+PP′+P′C′≥EC',
∴PB′+PP′+P′C′≥12+4﹣4,
∴PB′+PP′+P′C′≥8+4,
∴PB′+PC+PD的最小值为8+4,
故答案为:8+4.
18.解:①:∵正方形ABCD中,AB=AD,∠B=∠ADC=∠C=90°
∴MN2=MC2+NC2
当MN=MC时,
MN2=2MC2,
∴MC2=NC2,
∴MC=NC,
∴BM=DN,
∴△ABM≌△ADN(SAS)
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM=22.5°,故①正确;
②:如图,将△ABM绕点A顺时针旋转90°得△ADE,
则∠EAN=∠EAM﹣∠MAN=90°﹣45°=45°,
则在△EAN和△MAN中,
,
∴△EAN≌△MAN(SAS)
∴∠AMN=∠AED,
∴∠AED+∠EAM+∠ENM+∠AMN=360°,
∴2∠AMN+90°+(180°﹣∠MNC)=360°,
∴2∠AMN﹣∠MNC=90°,
故②正确;
③:∵△EAN≌△MAN,
∴MN=EN=DE+DN=BM+DN,
∴△MNC的周长为:
MC+NC+MN=(MC+BM)+(NC+DN)=DC+BC,
∵DC和BC均为正方形ABCD的边长,故△MNC的周长不变.故③正确;
④如图,将△ADN绕点A逆时针旋转90°得△ABF,
∴∠MAF=90°﹣∠MAN=45°,
∴∠MAN=∠MAF,
在△MAN和△MAF中,
,
∴△MAN≌△MAF(SAS),
∴∠AMN=∠AMB,
故④错误.
综上①②③正确.
故答案为:①②③.
三.解答题(共8小题,满分66分)
19.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC==10,
∴AD=BC=DF=10,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
20.解:(1)若四边形AECF为平行四边形,
∴AO=OC,EO=OF,
∵四边形ABCD为平行四边形,
∴BO=OD=6cm,
∴EO=6﹣t,OF=2t,
∴6﹣t=2t,
∴t=2s,
∴当t为2秒时,四边形AECF是平行四边形;
(2)若四边形AECF是菱形,
∴AC⊥BD,
∴AO2+BO2=AB2,
∴AB==3;
∴当AB为3时, AECF是菱形;
(3)∵四边形AECF是菱形,
∴BO⊥AC,OE=OF,
∵四边形ABCD是平行四边形,
∴BO=OD,
∴BE=DF,
∴t=6﹣2t,
∴t=2,
∴BE=DF=2,
∴EF=8,
∴菱形AECF的面积=AC EF=6×8=24.
21.解:(1)∵证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD中点,
∴OB=OD,
在△PDO和△QBO中,
,
∴△PDO≌△QBO(ASA),
∴OP=OQ.
又∵OB=OD,
∴四边形PBQD是平行四边形;
(2)依题意得,AP=tcm,则PD=(6﹣t) cm.
当四边形PBQD是菱形时,有PB=PD=(6﹣t) cm.
∵四边形ABCD是矩形,
∴∠A=90°.
在Rt△ABP中,AP2+AB2=BP2,AB=4cm,
∴t2+42=(6﹣t)2
解得,
所以运动的时间为时,四边形PBQD是菱形.
∴此时菱形的周长为(cm).
22.(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPE=∠EDF=90°;
(3)解:AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
23.解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
24.证明:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
25.(1)证明:∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠DAB=∠GAE=90°,
∴∠GAD=∠EAB,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
26.解:(1)图1中的结论仍然成立,即BM+DN=MN,理由为:
如图2,在MB的延长线上截取BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠DAB=∠ABC=∠ABE=90°,
∵在△ABE和△ADN中
,
∴△ABE≌△ADN(SAS).
∴AE=AN;∠EAB=∠NAD,
∵∠DAB=90°,∠MAN=45°,
∴∠DAN+∠BAM=45°,
∴∠EAM=∠BAM+∠EAB=45°=∠MAN,
∵在△AEM和△ANM中
,
∴△AEM≌△ANM(SAS),
∴ME=MN,
∴MN=ME=BE+BM=DN+BM,
即DN+BM=MN;
(2)猜想:线段BM,DN和MN之间的等量关系为:DN﹣BM=MN.
证明:如图3,在DN上截取DE=MB,连接AE,
∵由(1)知:AD=AB,∠D=∠ABM=90°,BM=DE,
∴△ABM≌△ADE(SAS).
∴AM=AE;∠MAB=∠EAD,
∵∠MAN=45°=∠MAB+∠BAN,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°﹣45°=45°=∠MAN,
∵在△AMN和△AEN中
,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵DN﹣DE=EN,
∴DN﹣BM=MN.
